2.3.1. Удельная проводимость и удельное сопротивление проводников
2.3.2. Температурный коэффициент удельного сопротивления металлов
2.3.3. Изменение удельного сопротивления металлов при плавлении
2.3.4. Изменение удельного сопротивления металлов при деформациях
2.3.5. Удельное сопротивление сплавов
2.3.6. Теплопроводность металлов
К важнейшим параметрам, характеризующим свойства проводниковых материалов, относятся:
- удельная проводимость g или обратная ей величина – удельное сопротивление r,
- температурный коэффициент удельного сопротивления ТКr или ar,
- теплопроводность g т,
- контактная разность потенциалов и термо-э.д.с.,
- работа выхода электронов из металла,
- предел прочности при растяжении sr и относительное удлинение при разрыве Dl/l.
2.3.1. Удельная проводимость и удельное сопротивление проводников
Связь плотности тока J, А/м2, и напряженности электрического поля Е, В/м, в проводнике дается известной формулой:
(2.1)
Здесь g, См/м – параметр проводникового материала, называемый его удельной проводимостью; в соответствии с законом Ома g не зависит от напряженности электрического поля при изменении последней в весьма широких пределах. Величина r=1/g, oбратная удельной проводимости и называемая удельным сопротивлением, для имеющего сопротивление R проводника длиной l с постоянным поперечным сечением S вычисляется по формуле
ρ = R·S/l. (2.2)
Единица СИ для удельного сопротивления - Ом·м. Диапазон значений удельного сопротивления ρ металлических проводников при нормальной температуре довольно узок: от 0.016 для серебра и до примерно 10 мкОм·м для железохромоалюминиевых сплавов, т.е. он занимает всего три порядка. Значение удельной проводимости γ в основном зависит от средней длины свободного пробега электронов в данном проводнике, которая, в свою очередь, определяется структурой проводникового материала. Все чистые металлы с наиболее правильной кристаллической решеткой характеризуются наименьшими значениями удельного сопротивления; примеси, искажая решетку, приводят к увеличению ρ. И с точки зрения волновой теории, рассеяние электронных волн происходит на дефектах кристаллической решетки, которые соизмеримы с расстоянием порядка четверти длины электронной волны. Нарушения меньших размеров не вызывают заметного рассеяния волн.
2.3.2. Температурный коэффициент удельного сопротивления металлов
Число носителей заряда в металлическом проводнике при повышении температуры остается практически неизменным. Однако вследствие колебаний узлов кристаллической решетки с ростом температуры появляется все больше и больше препятствий на пути направленного под действием электрического поля движения свободных электронов, т.е. уменьшается средняя длина свободного пробега электрона, уменьшается подвижность электронов и, как следствие, уменьшается удельная проводимость металлов, и увеличивается удельное сопротивление. Иными словами, температурный коэффициент удельного сопротивления металлов положителен.
2.3.3. Изменение удельного сопротивления металлов при плавлении
При переходе из твердого состояния в жидкое у большинства металлов наблюдается увеличение удельного сопротивления, как это видно из рис.2.1; однако некоторые металлы при плавлении повышают ρ.
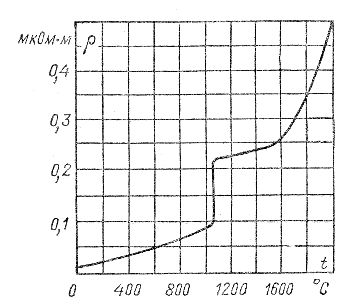
Рис.2.1. Зависимость удельного сопротивления меди от температуры.
Скачок соответствует температуре плавления меди 1083°С
Удельное сопротивление увеличивается при плавлении у тех металлов, которые при плавлении увеличивают объем, т.е. уменьшают плотность; у металлов с противоположным характером изменения объема при плавлении (аналогичным фазовому переходу лед-вода) ρ уменьшается.
2.3.4. Изменение удельного сопротивления металлов при деформациях
Изменение удельного сопротивления при растяжении или сжатии приближенно может оцениваться формулой
ρ = ρ0 (1± σ ·s) , (2.3)
где ρ - удельное сопротивление металла при механическом напряжении σ, ρ0 – удельное сопротивление металла, не подверженного механическому воздействию, s – коэффициент механического напряжения, характеризующий данный металл; знак плюс в формуле соответствует растяжению, минус – сжатию.
Изменение ρ при упругих деформациях объясняется изменением амплитуды колебаний узлов кристаллической решетки металла. При растяжении эти амплитуды увеличиваются, при сжатии – уменьшаются. Увеличение амплитуды колебаний узлов кристаллической решетки приводит к уменьшению подвижности носителей зарядов и, как следствие, к возрастанию ρ. Пластическая деформация, как правило, повышает удельное сопротивление металлов вследствие искажения кристаллической решетки. При рекристаллизации путем отжига удельное сопротивление может быть вновь снижено до первоначального значения.
2.3.5. Удельное сопротивление сплавов
Значительное возрастание ρ наблюдается при сплавлении двух металлов в том случае, если они образуют друг с другом твердый раствор, т.е. создают при отвердевании совместную кристаллизацию, и атомы одного металла входят в кристаллическую решетку другого. ρ имеет максимум, соответствующий некоторому определенному соотношению между содержанием компонентов в сплаве. Так, Н.С.Курнаков открыл, что в тех случаях, когда при определенном соотношении между компонентами они образуют друг с другом явно выраженные химические соединения (интерметаллиды), на кривых ρ в функции состава наблюдаются изломы (рис.2.2).
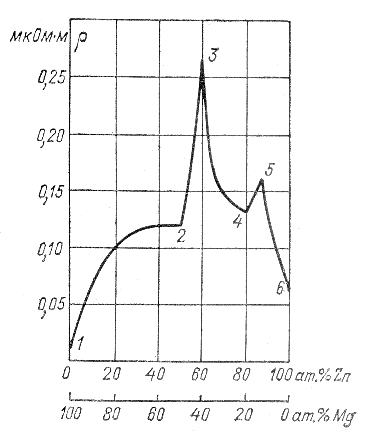
Рис. 2.2. Зависимость удельного сопротивления сплавов цинк – магний от состава. Точка 1 соответствует чистому Mg, 2 – соединению MgZn, 3 - Mg2Zn3, ., 4 – MgZn4 5 – MgZn6, 6 – чистому Zn.
Исследования А.Ф.Иоффе показали, что многие интерметаллиды являются не веществами с металлическим характером электропроводности, а электронными полупроводниками.
Если же сплав двух металлов создает раздельную кристаллизацию, и структура застывшего сплава представляет собой смесь кристаллов каждого из компонентов (т.е. искажение кристаллической решетки каждого компонента не имеет места), то удельная проводимость γ сплава меняется с изменением состава приблизительно линейно, т.е. определяется арифметическим правилом смешения (рис.2.3).
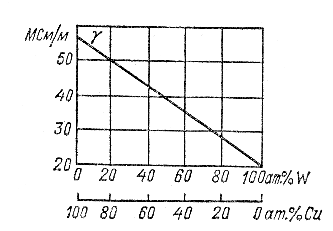
Рис.2.3. Зависимость удельной проводимости сплавов медь – вольфрам от состава (в процентах по массе)
2.3.6. Теплопроводность металлов
За передачу тепла через металл в основном ответственны те же свободные электроны, которые определяют и электропроводность металлов, и количество которых в единице объема весьма велико. Поэтому, как правило, теплопроводность γт металлов намного больше, чем теплопроводность диэлектриков. Очевидно, что при прочих равных условиях, чем больше удельная электрическая проводимость γ металла, тем больше должна быть и его теплопроводность. Легко также видеть, что при повышении температуры, когда подвижность электронов в металле и соответственно его удельная проводимость уменьшаются, отношение γт/γ δ должно возрастать.
Чистота и характер механической обработки металла могут заметно сказываться на его теплопроводности, в особенности при низких температурах.
2.3.7. Термоэлектродвижущая сила
При соприкосновении двух металлических проводников между ними возникает контактная разность потенциалов. Причина ее появления заключается в различии значений работы выхода электронов из различных металлов, а также в том, что концентрация электронов, а следовательно, и давление электронного газа у разных металлов и сплавов могут быть неодинаковыми. Из электронной теории металлов следует, что контактная разность потенциалов между металлами А и В равна:
(2.4)
где UА и UВ – потенциалы соприкасающихся металлов; nА и nВ – концентрации электронов в металлах А и В.
Если температуры "спаев" одинаковы, то сумма разностей потенциалов равны нулю. Иначе обстоит дело, когда один металл имеет температуру Т1, а другой – Т2.
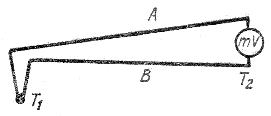Рис.2.4.Схема термопары
В этом случае между "спаями" возникает термо-э.д.с., равная
(2.5)
что можно записать в виде
(2.6)
Где с – постоянный для данной пары проводников коэффициент термо-э.д.с., т.е. термо-э.д.с. должна быть пропорциональна разности температур металлов.
Провод, составленный из двух изолированных друг от друга проволок из различных металлов или сплавов (термопара), может быть использован для измерения температур.
2.3.8. Механические свойства проводников
Они характеризуются пределом прочности при растяжении σр и относительным удлинением при разрыве Δl/l, а так же хрупкостью, твердостью и тому подобными свойствами. Механические свойства металлических проводников в большой степени зависят от механической и термической обработки, от наличия легирующих примесей и т.п. Влияние отжига приводит к существенному уменьшению σр и увеличению Δl/l. Такие параметры проводниковых материалов, как температуры кипения и плавления, удельная теплоемкость и др., не требуют особых пояснений.