12.4.1. Пример использования скачкообразной перестройки частоты
12.4.3. Одновременное использование скачкообразной перестройки частоты и разнесения сигнала
В данном разделе рассматривается метод скачкообразной перестройки частоты (frequency hopping — FH). Для модуляции в данной схеме обычно используется M-арная частотная манипуляция (M-ary frequency shift keying— MFSK). При этой модуляции k=log2M информационных бит используются для определения одной из М передаваемых частот. Положение М-арного множества сигналов скачкообразно изменяется синтезатором частот на псевдослучайную величину, принадлежащую полосе Wss. На рис. 12.11 представлена блок-схема системы FH/MFSK наиболее распространенного типа. В обычной системе MFSK несущая с фиксированной частотой модулируется символом данных; в системе FH/MFSK частота несущей является псевдослучайной. В обоих случаях передается один тон. Систему FH на рис. 12.11 можно рассматривать как двухэтапный процесс модуляции — модуляции информации и модуляции с перестройкой частоты — хотя он может быть реализован и как один этап, когда синтезатор частот производит тон передачи, основываясь на псевдослучайном коде и информационной последовательности. При каждом скачке генератор псевдослучайного сигнала передает синтезатору частот частотное слово (последовательность из l элементарных сигналов), которое определяет одну из 2' позиций множества символов. Минимальное разнесение по частоте между последовательными скачками 
и шириной полосы перестройки частот Wss определяет минимальное количество элементарных сигналов частотного слова.
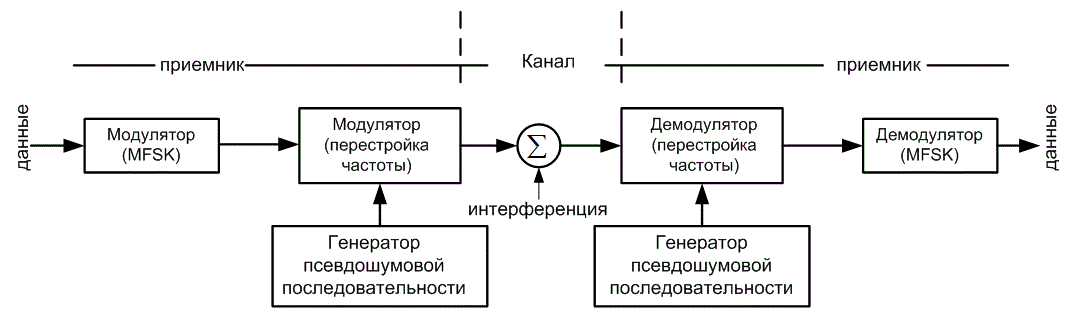
Рис. 12.11. Система FH/MFSK
Для данного скачка ширина полосы, необходимая для передачи, будет такой же, как и в обычной схеме MFSK, что, как правило, намного меньше Wss. В то же время при усреднении по множеству скачков спектр FH/MFSK будет занимать всю полосу расширенного спектра. Метод расширенного спектра позволяет для перестройки частоты использовать полосы шириной порядка несколько гигагерц, что намного превышает аналогичные показатели систем DS [8]. Следовательно, коэффициент расширения спектра сигнала систем FH будет значительно больше. Из-за использования в случае FH полос значительной ширины сохранение фазовой когерентности от скачка к скачку является нелегкой задачей. Поэтому обычно в таких системах применяется некогерентная демодуляция. Рассмотрение когерентных систем с скачкообразной перестройкой частоты представлено в работе [9].
Как видно из рис. 12.11, приемник повторяет все операции передатчика в обратной последовательности. Полученный сигнал демодулируется путем наложения той же псевдослучайной тоновой последовательности, что использовалась для перестройки частоты. После этого сигнал обрабатывается стандартным набором из М некогерентных детекторов энергии с целью выбора наиболее вероятного символа.
Пример 12.1. Размер частотного слова
Ширина полосы системы Wss равна 400 МГц; минимальное изменение частоты =100 Гц. Определите минимальное число элементарных сигналов псевдослучайного кода, необходимое для создания частотного слова.
Решение
Число тонов, содержащихся в Wss, равно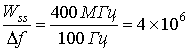 
Минимальное число элементарных сигналов =
,
где 
— наименьшее целое, не превышающее х.
12.4.1. Пример использования скачкообразной перестройки частоты
Рассмотрим пример системы с перестройкой частоты, приведенный на рис. 12.12. Входные данные состоят из двоичной последовательности, характеризуемой скоростью передачи данных R=150 бит/с. Модуляция — 8-FSK. Таким образом, скорость передачи символов равна Rs=R/(1оg28)=50 символов/с (длительность передачи одного символа Т=1/50=20мс). Изменение частоты происходит после передачи отдельного символа, причем скачки синхронизированы во времени с границами символов. Следовательно, скорость скачкообразной перестройки частоты равна 50 скачков/с. На рис. 12.12 представлен график зависимости ширины полосы частот (ось ординат, Wss) от времени (ось абсцисс). Приведенные условные обозначения иллюстрируют присвоение восьмеричных символов FSK частотным тонам. Следует отметить, что разнесение тонов, определенное как 1/Т=50 Гц, соответствует минимальному значению, которое необходимо для передачи ортогональных сигналов для данной некогерентной системы FSK (см. раздел 4.5.4).
Типичная двоичная информационная последовательность представлена в верхней части рис. 12.12. При использовании модуляции 8-FSK символы формируются из трех бит. При обычной модуляции 8-FSK производится передача однополосного тонового сигнала, полученного в соответствии с представленной на рисунке схемой присвоения. Тоновый сигнал сдвинут по отношению к f0, фиксированному центру частотного диапазона данных. Единственным отличием метода FH/MFSK от MFSK является то, что f0 не фиксирована. При передаче очередного символа f0 перескакивает на новую частоту, и вместе с ней перемещается вся структура диапазона данных. На рис. 12.12 первый символ последовательности данных, 011, соответствует тоновому сигналу, который на 25 Гц выше по отношению к f0. На рисунке пунктирная линия соответствует f0, непрерывная — тоновому сигналу. Во время передачи второго символа f0 переходит в новое положение, обозначенное пунктиром. Второй символ, 110, задает тоновый сигнал на 125 Гц ниже по отношению к f0. Подобным образом последний символ последовательности (00 1) соответствует сигналу, смещенному вверх на 125 Гц по отношению к центру диапазона. Центр частотного диапазона в последнем случае смещается, однако относительное расположение тонов остается прежним.
12.4.2. Устойчивость
В повседневной жизни под устойчивостью (robustness) подразумевают силу и выносливость. В контексте систем связи значение этого слова практически не отличается от обыденного. Уровень устойчивости определяет способность сигнала выдерживать искажения в канале (шумы, намеренные помехи, замирание сигнала и т. п.). Вероятность получения сигнала, несколько копий которого передаются на разных частотах, выше, чем в случае единичного сигнала, равного по мощности сумме всех копий. Чем выше разнесение сигнала (разнесенные во времени множественные передачи на разных частотах), тем выше его устойчивость к случайным помехам.
Следующий пример позволит лучше понять смысл сказанного выше. Рассмотрим сообщение, состоящее из четырех символов: s1,s2,s3,s4. Разнесение можно начать с N-кратного повторения сообщения. Пусть N равно 8. Тогда последовательность символов, называемых элементарными сигналами (chips), можно записать в следующем виде.
s1 s1 s1 s1 s1 s1 s1 s1 s2 s2 s2 s2 s2 s2 s2 s2 s3 s3 s3 s3 s3 s3 s3 s3 s4 s4 s4 s4 s4 s4 s4 s4
Каждый из элементарных сигналов передается на отдельной частоте (центр диапазона данных сдвигается при передаче каждого символа). Серия сигналов на частотах fi ,fj ,fk ... более устойчива к помехам, чем сигнал без такого разнесения. Простым аналогом данного примера может быть сравнение выстрела дробью с выстрелом пулей. Вероятность того, что одна из множества дробинок попадет в цель, выше, чем для одной крупной пули.
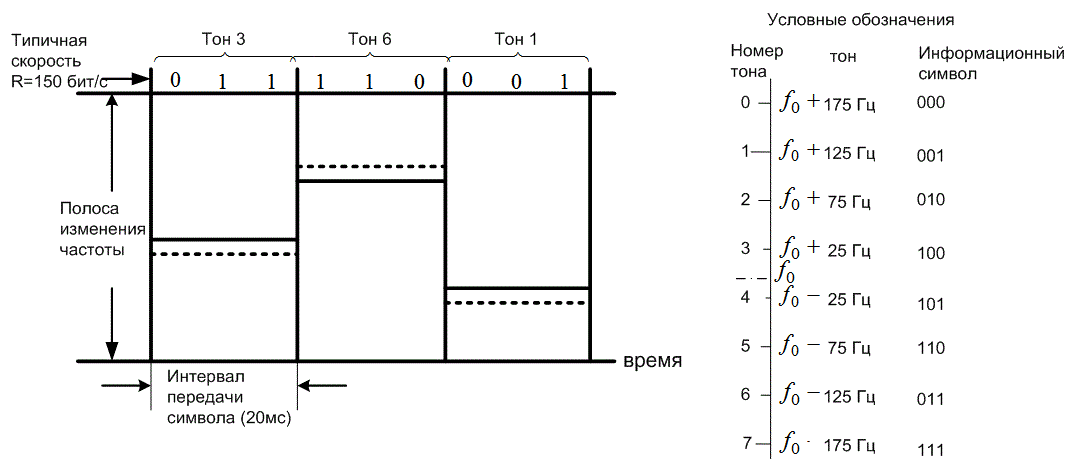
Рис.12.12. Пример системы связи с использованием скачкообразной перестройки частоты и модуляции 8-FSK
12.4.3. Одновременное использование скачкообразной перестройки частоты и разнесения сигнала
В примере, изображенном на рис. 12.13, каждый из элементарных сигналов передается четыре раза (N=4), в остальном данный случай аналогичен представленному на рис. 12.12. Каждый из интервалов передачи символа (20 мс) разбит на четыре части, которые соответствуют количеству передаваемых элементарных сигналов. Последовательность данных остается такой же, как и для рис. 12.12, и характеризуется скоростью R=150 бит/с. Прежним остается и трехбитовое разбиение с целью формирования 8-ричных символов. Каждый символ передается четырежды, причем для каждого сеанса передачи генератор псевдослучайного кода изменяет центральную частоту диапазона передачи. Следовательно, для данного случая время передачи элементарного сигнала Тсравно T/N = 20 мс/4 = 5 мс. Скорость перестройки частоты равна следующему.
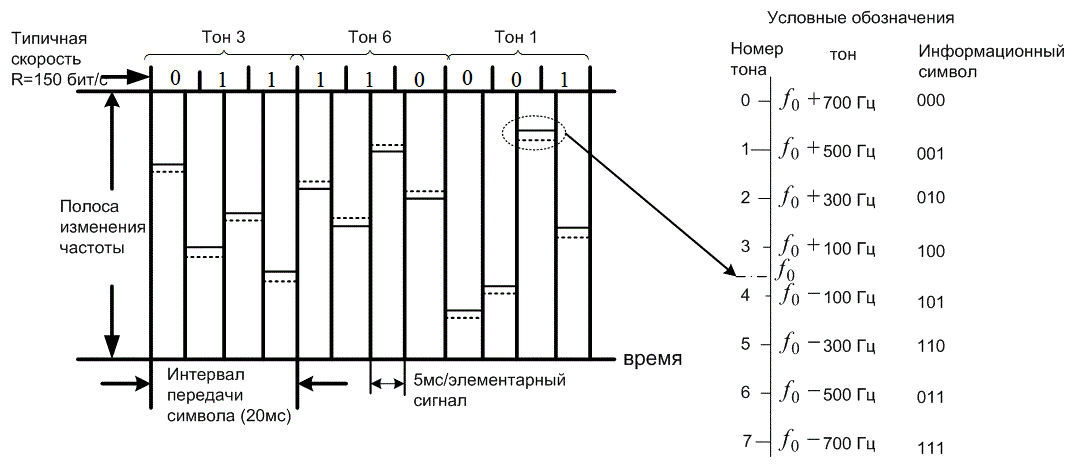
Рис.12.13. Пример одновременного использования скачкообразной перестройки частоты и разнесения (N=4)
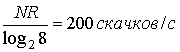
Следует отметить, что разнесение тонов должно изменяться таким образом, чтобы удовлетворялось требование ортогональности. Поскольку длительность тонов FSK в данном примере равна длительности передачи элементарного сигнала (Tс=T/N), минимальное расстояние между тонами 1/Тс=N/T=200 Гц. Как и в предыдущем примере, на рис. 12.13 показано смещение центра диапазона передачи данных (и модулирующей структуры) при передаче каждого из элементарных сигналов. Частота передачи (сплошная линия) и центр диапазона передачи данных (пунктир) соотносятся между собой так же, как для каждого из элементарных сигналов, соответствующих определенному символу (рис. 12.12).
12.4.4. Быстрая и медленная перестройка частоты
В системах расширения спектра методом прямой последовательности термин "элементарный символ" означает символ псевдослучайного кода (наиболее короткий символ системы DS). В системе с перестройкой частоты тот же термин обозначает кратчайший непрерывный сигнал. Различают системы связи медленной (slow-frequency hopping — SFH) и быстрой (fast-frequency hopping — FFH) перестройки- частоты. Для системы SFH кратчайший непрерывный сигнал — это информационный символ. В случае FFH — это скачок частоты. На рис. 12.14, а представлена система FFH со скоростью передачи данных 30 символов/с и скоростью изменения частоты 60 скачков/с. На рисунке показан сигнал s(t) в течение времени передачи одного символа (1/30 с). Изменение формы сигнала в центре графика s(t) связано с очередной скачкообразной перестройкой частоты. В данном примере элементарный сигнал соответствует изменению частоты, поскольку время перестройки меньше длительности символа. Каждый элементарный сигнал соответствует половине символа. На рис. 12.14, б иллюстрируется использование системы SFH. Скорость передачи данных по-прежнему равна 30 символов/с; скорость изменения частоты — 10 скачков/с. Сигнал s(t) изображен на протяжении времени передачи трех элементарных сигналов (1/10 с). В данном примере скачки частоты происходят в начале и конце последовательности из трех символов. Форма сигнала меняется вследствие изменений режима модуляции. Теперь элементарный сигнал соответствует информационному символу, длительность которого меньше интервала между изменениями частоты.
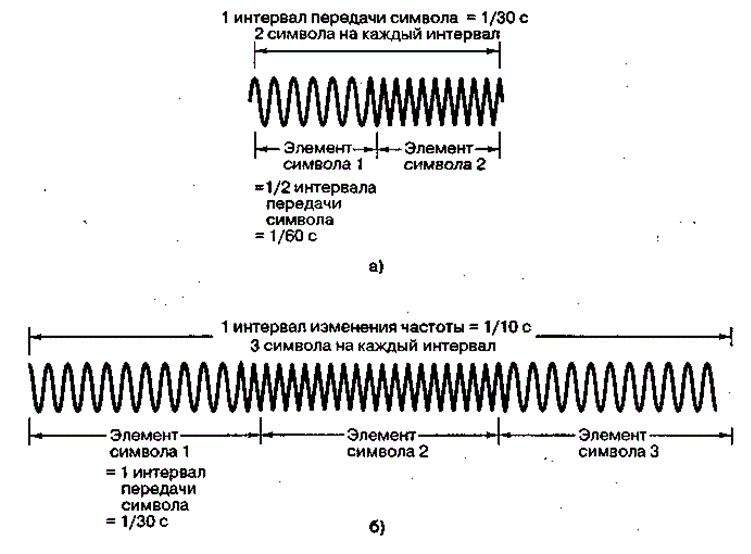
Рис.12.14. Элементарный сигнал в системах FH|MFSK: а) система MFSK с скачкообразной перестройкой частоты, скорость передачи данных 30 символов/с, скорость изменения частоты 60 скачков/с, 1 элементарный сигнал=1 интервал между скачками частоты; б) то же, но скорость изменения частоты 10 скачков/с, 1 элементарный сигнал=1 символ.
На рис. 12.15, а представлен пример двоичной системы FSK с использованием FFH. Сигнал разделен на N=4 части, т.е. 4 элементарных сигнала соответствуют одному биту. Как и на рис. 12.13, пунктир показывает центр диапазона передачи данных, а непрерывная линия — частоту символа. В данном случае длительность элементарного сигнала равна интервалу между скачками частоты. На рис. 12.15, б представлен пример системы FSK с использованием SFH. В этом случае в течение промежутка между скачками частоты производится передача трех бит. В данной схеме SFH длительность элементарного сигнала равна времени передачи одного бита. Каким было бы время передачи элементарного сигнала, если бы в последнем примере система была не двоичной, а восьмеричной, т.е. каждые 3 бит передавались бы как один информационный символ? В этом случае временные границы символа и интервала между скачками частоты совпадали бы. Таким образом, длительность передачи элементарного сигнала, интервал между скачками частоты и время передачи символа были бы одинаковы.
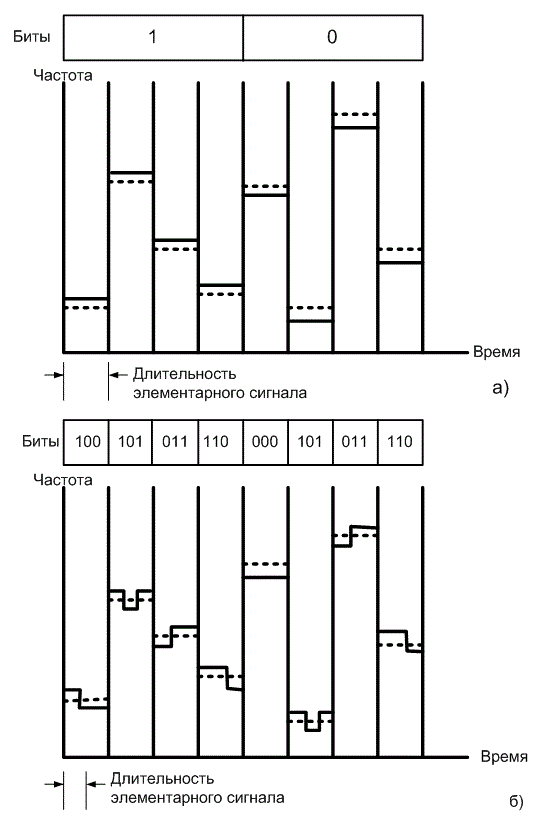
Рис.12.15. двоичные системы связи с использованием быстрой и медленной перестройки частоты: а) быстрая перестройка частоты: 4 скачка/бит; б) медленная перестройка частоты: 3 бит/скачок.
12.4.5. Демодулятор FFH/MFSK
На рис. 12.16 приводится схема стандартного демодулятора MFSK в системе с быстрой скачкообразной перестройкой частоты (FFH/MFSK). Обработка сигнала начинается с обращения скачков частоты. Для этого используется генератор псевдослучайной последовательности, аналогичный существующему в передатчике. После прохождения через фильтр нижних частот ширина полосы сигнала становится равной ширине полосы данных. Затем сигнал демодулируется с использованием блока из М детекторов энергии (или детекторов огибающей). За каждым детектором следует схема одностороннего ограничения и накопитель. Схемы ограничения играют важную роль при наличии намеренных помех; их применение будет подробно рассмотрено ниже. Следует отметить, что демодулятор не принимает решения относительно значения символов на основе изучения отдельных элементарных сигналов. Вместо этого после получения энергии N элементарных сигналов и после того, как энергия N-гo сигнала сложится с энергиями предыдущих N-1 сигналов, демодулятор принимает решение, выбирая символ, соответствующий накопителю г/ (i= 1, 2, ..., М) с максимальной энергией.
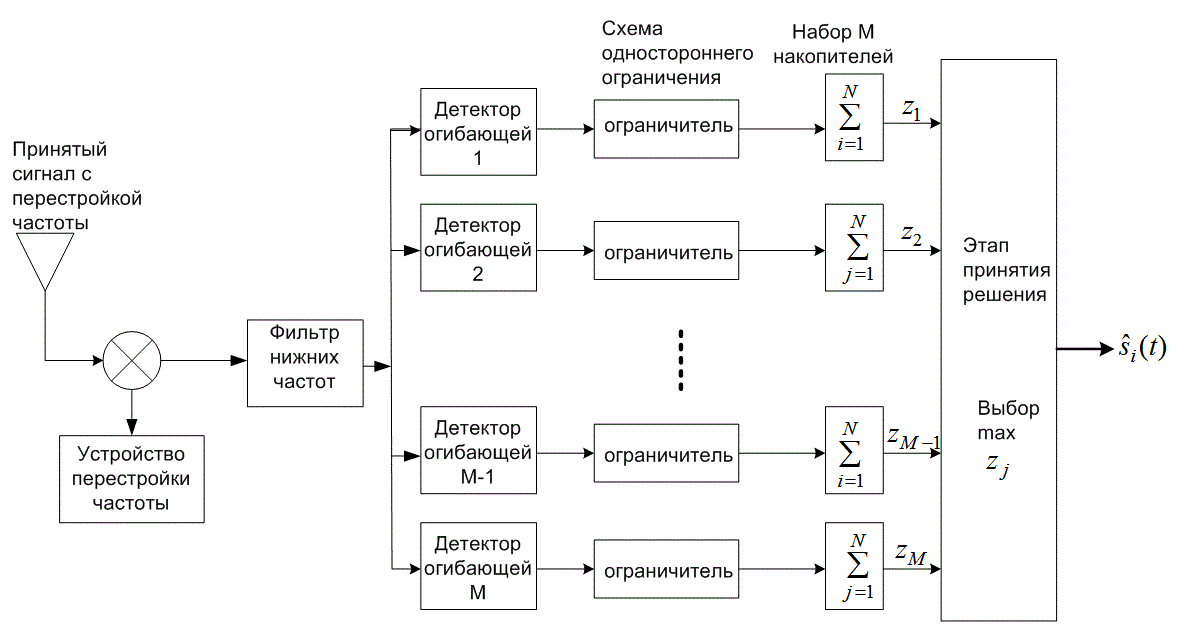
Рис. 12.16. Демодулятор FFH/MFSK
12.4.6. Коэффициент расширения спектра сигнала
В уравнении (12.27) приводится общее выражение для коэффициента расширения спектра сигнала: Gp=Wss/R. Для системы расширения спектра методом прямой последовательности величина Wss равна скорости передачи элементарных сигналов Rch. При использовании скачкообразной перестройки частоты уравнение (12.27) также выражает коэффициент расширения спектра, однако значение Wss равно ширине полосы частот, в пределах которой может происходить изменение частоты. Данную полосу называют полосой перестройки (hopping band) Wh. Таким образом, коэффициент расширения спектра сигнала для системы со скачкообразной перестройкой частоты можно записать в следующем виде.
(12.29)