3.1.1. Рост вероятности ошибки в системах связи
3.1.2. Демодуляция и обнаружение
3.1.3. Векторное представление сигналов и шума
3.1.3.2. Обобщенное преобразование Фурье
3.1.3.3. Представление белого шума через ортогональные сигналы
3.1.4. Важнейший параметр систем цифровой связи - отношение сигнал/шум
3.1.5. Почему отношение
- это естественный критерий качества
3.1.1. Рост вероятности ошибки в системах связи
Задача детектора - максимально безошибочно угадать принятый сигнал, насколько это возможно при данном ухудшении качества сигнала в процессе передачи. Существует две причины роста вероятности ошибки. Первая - это последствия фильтрации в передатчике, канале и приемнике, рассмотренные в разделе 3.3. В этом разделе показано, что неидеальная передаточная функция системы приводит к «размыванию» символов, или межсимвольной интерференции (intersymbol interference - ISI).
Вторая причина роста вероятности ошибки - электрические помехи, порождаемые различными источниками, такими как галактика и атмосфера, импульсные помехи, комбинационные помехи, а также интерференция с сигналами от других источников. (Этот вопрос подробно рассмотрен в главе 5.) При надлежащих мерах предосторожности можно устранить большую часть помех и уменьшить последствия интерференции.
В то же время существуют помехи, устранить которые нельзя; это - помехи, вызываемые тепловым движением электронов в любой проводящей среде. Это движение порождает в усилителях и каналах связи тепловой шум, который аддитивно накладывается на сигнал. Использование квантовой механики позволило разработать хорошо известную статистику теплового шума [1].
Основная статистическая характеристика теплового шума заключается в том, что его амплитуды распределены по нормальному или гауссову закону распределения, рассмотренному в разделе 1.5.5 (рис. 1.7). На этом рисунке показано, что наиболее вероятные амплитуды шума - амплитуды с небольшими положительными или отрицательными значениями. Теоретически шум может быть бесконечно большим, но на практике очень большие амплитуды шума крайне редки. Основная спектральная характеристика теплового шума в системе связи заключается в том, что его двусторонняя спектральная плотность мощности ![]() является плоской для всех частот, представляющих практический интерес. Другими словами, в тепловом шуме в среднем на низкочастотные флуктуации приходится столько же мощности на герц, сколько и на высокочастотные флуктуации - вплоть до частоты порядка
является плоской для всех частот, представляющих практический интерес. Другими словами, в тепловом шуме в среднем на низкочастотные флуктуации приходится столько же мощности на герц, сколько и на высокочастотные флуктуации - вплоть до частоты порядка ![]() герц. Если мощность шума характеризуется постоянной спектральной плотностью мощности, шум называется белым. Поскольку тепловой шум присутствует во всех системах связи и для многих систем является доминирующим источником помех, характеристики теплового шума часто используются для моделирования шума при обнаружении и проектировании приемников. Всякий раз, когда канал связи определен как канал AWGN (при отсутствии указаний на другие параметры, ухудшающие качество передачи), мы, по сути, говорим, что ухудшение качества сигнала связано исключительно с неустранимым тепловым шумом.
герц. Если мощность шума характеризуется постоянной спектральной плотностью мощности, шум называется белым. Поскольку тепловой шум присутствует во всех системах связи и для многих систем является доминирующим источником помех, характеристики теплового шума часто используются для моделирования шума при обнаружении и проектировании приемников. Всякий раз, когда канал связи определен как канал AWGN (при отсутствии указаний на другие параметры, ухудшающие качество передачи), мы, по сути, говорим, что ухудшение качества сигнала связано исключительно с неустранимым тепловым шумом.
3.1.2. Демодуляция и обнаружение
В течение данного интервала передачи сигнала, Т, бинарная узкополосная система передает один из двух возможных сигналов, обозначаемых как ![]() и
и ![]() . Подобным образом бинарная полосовая система передает один из двух возможных сигналов, обозначаемых как
. Подобным образом бинарная полосовая система передает один из двух возможных сигналов, обозначаемых как ![]() и
и ![]() . Поскольку общая трактовка демодуляции и обнаружения, по сути, совпадает для узкополосных и полосовых систем, будем использовать запись
. Поскольку общая трактовка демодуляции и обнаружения, по сути, совпадает для узкополосных и полосовых систем, будем использовать запись ![]() для обозначения передаваемого сигнала, вне зависимости от того, является система узкополосной или полосовой. Это позволяет совместить многие аспекты демодуляции/обнаружения в узкополосных системах, рассмотренные в данной главе, с соответствующими описаниями для полосовых систем, рассмотренных в главе 4. Итак, для любого канала двоичный сигнал, переданный в течение интервала
для обозначения передаваемого сигнала, вне зависимости от того, является система узкополосной или полосовой. Это позволяет совместить многие аспекты демодуляции/обнаружения в узкополосных системах, рассмотренные в данной главе, с соответствующими описаниями для полосовых систем, рассмотренных в главе 4. Итак, для любого канала двоичный сигнал, переданный в течение интервала ![]() , представляется следующим образом.
, представляется следующим образом.
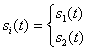
![]()
![]()
![]()
![]()
Принятый сигнал ![]() искажается вследствие воздействия шума
искажается вследствие воздействия шума ![]() и, возможно, неидеальной импульсной характеристики канала
и, возможно, неидеальной импульсной характеристики канала ![]() и описывается следующей формулой (1.1).
и описывается следующей формулой (1.1).
![]() (3.1)
(3.1)
В нашем случае ![]() предполагается процессом AWGN с нулевым средним, а знак «*» обозначает операцию свертки. Для бинарной передачи по идеальному, свободному от искажений каналу, где свертка с функцией
предполагается процессом AWGN с нулевым средним, а знак «*» обозначает операцию свертки. Для бинарной передачи по идеальному, свободному от искажений каналу, где свертка с функцией ![]() не ухудшает качество сигнала (поскольку для идеального случая
не ухудшает качество сигнала (поскольку для идеального случая ![]() - импульсная функция), вид
- импульсная функция), вид ![]() можно упростить.
можно упростить.
![]()
![]()
![]() (3.2)
(3.2)
Типичные функции демодуляции и обнаружения цифрового приемника показаны на рис. 3.1. Некоторые авторы используют термины «демодуляция» и «обнаружение» как синонимы. Демодуляцию (demodulation) мы определим как восстановление сигнала (в неискаженный узкополосный импульс), а обнаружение (detection) - как процесс принятия решения относительно цифрового значения этого сигнала. При отсутствии кодов коррекции ошибок на выход детектора поступают аппроксимации символов (или битов) сообщений ![]() (также называемые жестким решением). При использовании кодов коррекции ошибок на выход детектора поступают аппроксимации канальных символов (или кодированных битов) и
(также называемые жестким решением). При использовании кодов коррекции ошибок на выход детектора поступают аппроксимации канальных символов (или кодированных битов) и ![]() имеющие вид жесткого или мягкого решения (см. раздел 7.3.2). Для краткости термин «обнаружение» иногда применяется для обозначения совокупности всех этапов обработки сигнала, выполняемых в приемнике, вплоть до этапа принятия решения. Блок преобразования с понижением частоты, показанный на рис. 3.1 в разделе демодуляции, отвечает за трансляцию полосовых сигналов, работающих на определенных радиочастотах. Эта функция может реализовываться различными способами. Она может выполняться на входе приемника, в демодуляторе, распределяться между этими двумя устройствами или вообще не реализовываться.
имеющие вид жесткого или мягкого решения (см. раздел 7.3.2). Для краткости термин «обнаружение» иногда применяется для обозначения совокупности всех этапов обработки сигнала, выполняемых в приемнике, вплоть до этапа принятия решения. Блок преобразования с понижением частоты, показанный на рис. 3.1 в разделе демодуляции, отвечает за трансляцию полосовых сигналов, работающих на определенных радиочастотах. Эта функция может реализовываться различными способами. Она может выполняться на входе приемника, в демодуляторе, распределяться между этими двумя устройствами или вообще не реализовываться.
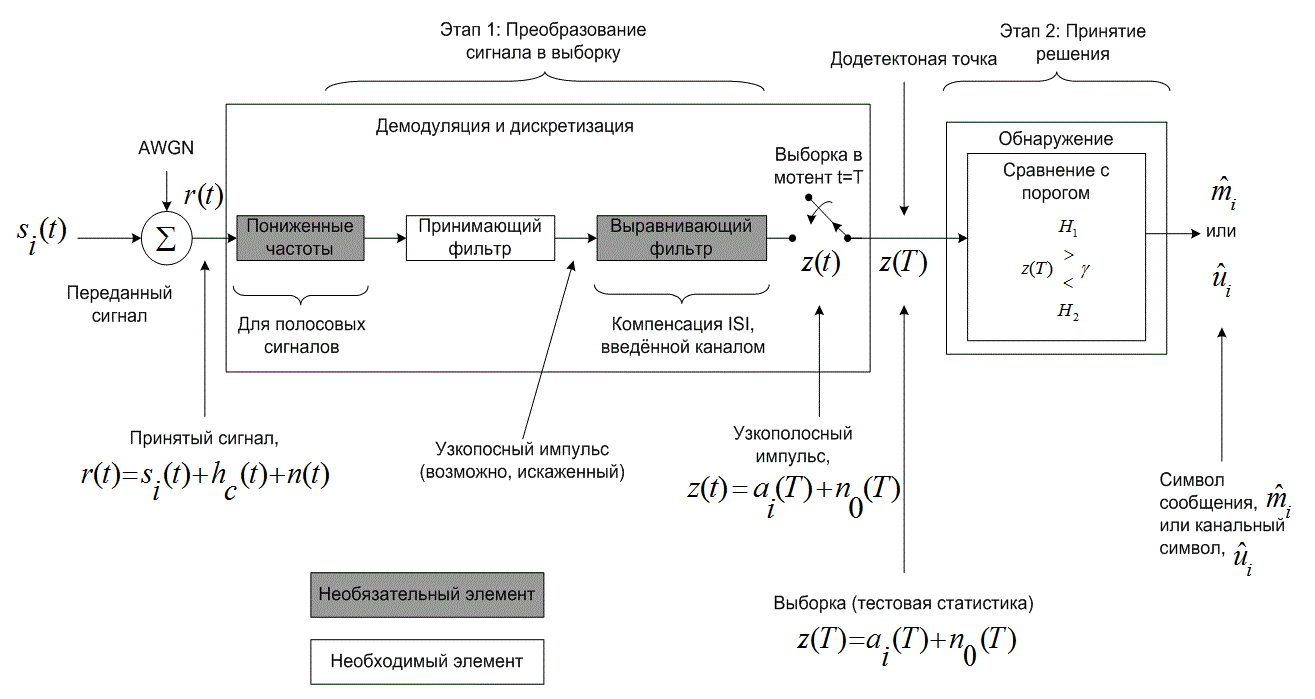
Рис.3.1. Два основных этапа в процессе демодуляции/ обнаружения цифровых сигналов
В блоке демодуляции и дискретизации (рис. 3.1) изображен принимающий фильтр (по сути, демодулятор), выполняющий восстановление сигнала в качестве подготовки к следующему необходимому этапу - обнаружению. Фильтрация в передатчике и канале обычно приводит к искажению принятой последовательности импульсов, вызванному межсимвольной интерференцией, а значит, эти импульсы не совсем готовы к дискретизации и обнаружению. Задачей принимающего фильтра является восстановление узкополосного импульса с максимально возможным отношением сигнал/шум (signal-to-noise ratio - SNR) и без межсимвольной интерференции. Оптимальный принимающий фильтр, выполняющий такую задачу, называется согласованным (matched), или коррелятором (correlator) и описывается в разделах 3.2.2 и 3.2.3. За принимающим фильтром может находиться выравнивающий фильтр (equalizing filter), или эквалайзер (equalizer); он необходим только в тех системах, в которых сигнал может искажаться вследствие межсимвольной интерференции, введенной каналом. Принимающий и выравнивающий фильтры показаны как два отдельных блока, что подчеркивает различие их функций. Впрочем, в большинстве случаев при использовании эквалайзера для выполнения обеих функций (а следовательно, и для компенсации искажения, внесенного передатчиком и каналом) может разрабатываться единый фильтр. Такой составной фильтр иногда называется просто выравнивающим или принимающим и выравнивающим.
На рис. 3.1 выделены два этапа процесса демодуляции/обнаружения. Этап 1, преобразование сигнала в выборку, выполняется демодулятором и следующим за ним устройством дискретизации. В конце каждого интервала передачи символа Т на выход устройства дискретизации, додетекторную точку, поступает выборка ![]() , иногда называемая тестовой статистикой. Значение напряжения выборки
, иногда называемая тестовой статистикой. Значение напряжения выборки ![]() прямо пропорционально энергии принятого символа и обратно пропорционально шуму. На этапе 2 принимается решение относительно цифрового значения выборки (выполняется обнаружение). Предполагается, что шум является случайным гауссовым процессом, а принимающий фильтр демодулятора - линейным. Линейная операция со случайным гауссовым процессом дает другой случайный гауссов процесс [2]. Следовательно, на выходе фильтра шум также является гауссовым. Значит, выход этапа 1 можно описать выражением
прямо пропорционально энергии принятого символа и обратно пропорционально шуму. На этапе 2 принимается решение относительно цифрового значения выборки (выполняется обнаружение). Предполагается, что шум является случайным гауссовым процессом, а принимающий фильтр демодулятора - линейным. Линейная операция со случайным гауссовым процессом дает другой случайный гауссов процесс [2]. Следовательно, на выходе фильтра шум также является гауссовым. Значит, выход этапа 1 можно описать выражением
![]()
![]() (3.3)
(3.3)
где ![]() - желаемый компонент сигнала, а
- желаемый компонент сигнала, а ![]() - шум. Для упрощения записи выражение (3.3) будем иногда представлять в виде
- шум. Для упрощения записи выражение (3.3) будем иногда представлять в виде ![]() . Шумовой компонент
. Шумовой компонент ![]() - это случайная гауссова переменная с нулевым средним, поэтому
- это случайная гауссова переменная с нулевым средним, поэтому ![]() - случайная гауссова переменная со средним
- случайная гауссова переменная со средним ![]() или
или ![]() , в зависимости от того, передавался двоичный нуль или двоичная единица. Как описывалось в разделе 1.5.5, плотность вероятности случайного гауссового шума
, в зависимости от того, передавался двоичный нуль или двоичная единица. Как описывалось в разделе 1.5.5, плотность вероятности случайного гауссового шума ![]() можно выразить как
можно выразить как
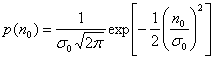 , (3.4)
, (3.4)
где ![]() - дисперсия шума. Используя выражения (3.3) и (3.4), можно выразить плотности условных вероятностей
- дисперсия шума. Используя выражения (3.3) и (3.4), можно выразить плотности условных вероятностей ![]() и
и ![]() .
.
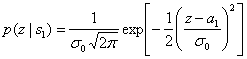 (3.5)
(3.5)
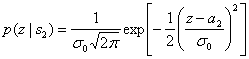 (3.6)
(3.6)
Эти плотности условных вероятностей показаны на рис. 3.2. Плотность ![]() , изображенная справа, называется правдоподобием
, изображенная справа, называется правдоподобием ![]() и показывает плотность вероятности случайной переменной
и показывает плотность вероятности случайной переменной ![]() при условии передачи символа
при условии передачи символа ![]() . Подобным образом функция
. Подобным образом функция ![]() (слева) является правдоподобием
(слева) является правдоподобием ![]() и показывает плотность вероятности
и показывает плотность вероятности ![]() при условии передачи символа
при условии передачи символа ![]() . Ось абсцисс,
. Ось абсцисс, ![]() , представляет полный диапазон возможных значений выборки, взятой в течение этапа 1, изображенного на рис. 3.1.
, представляет полный диапазон возможных значений выборки, взятой в течение этапа 1, изображенного на рис. 3.1.
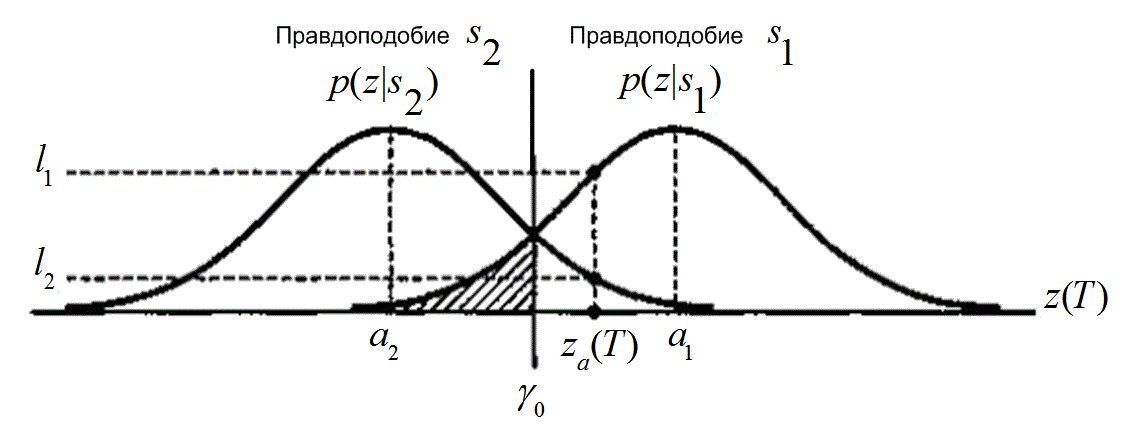
Рис.3.2. Плотности условных вероятностей: ![]() и
и ![]()
После того как принятый сигнал преобразован в выборку, действительная форма сигнала уже не имеет значения; сигналы всех типов, преобразованные в одинаковое значение ![]() , идентичны для схемы обнаружения. Далее будет показано, что оптимальный принимающий фильтр (согласованный фильтр) на этапе 1 (рис. 3.1) отображает все сигналы с равными энергиями в одну и ту же точку
, идентичны для схемы обнаружения. Далее будет показано, что оптимальный принимающий фильтр (согласованный фильтр) на этапе 1 (рис. 3.1) отображает все сигналы с равными энергиями в одну и ту же точку ![]() . Следовательно, важным параметром процесса обнаружения является энергия (а не форма) принятого сигнала, именно поэтому анализ обнаружения для узкополосных сигналов не отличается от анализа для полосовых сигналов. Поскольку
. Следовательно, важным параметром процесса обнаружения является энергия (а не форма) принятого сигнала, именно поэтому анализ обнаружения для узкополосных сигналов не отличается от анализа для полосовых сигналов. Поскольку ![]() является сигналом напряжения, пропорциональным энергии принятого символа, то чем больше амплитуда
является сигналом напряжения, пропорциональным энергии принятого символа, то чем больше амплитуда ![]() , тем более достоверным будет процесс принятия решения относительно цифрового значения сигнала. На этапе 2 обнаружение выполняется посредством выбора гипотезы, являющейся следствием порогового измерения
, тем более достоверным будет процесс принятия решения относительно цифрового значения сигнала. На этапе 2 обнаружение выполняется посредством выбора гипотезы, являющейся следствием порогового измерения
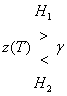 , (3.7)
, (3.7)
где ![]() и
и ![]() - две возможные (бинарные) гипотезы. Приведенная запись указывает, что гипотеза
- две возможные (бинарные) гипотезы. Приведенная запись указывает, что гипотеза ![]() выбирается при
выбирается при ![]() , а
, а ![]() - при
- при ![]() . Если
. Если ![]() , решение может быть любым. Выбор
, решение может быть любым. Выбор ![]() , равносилен тому, что передан был сигнал
, равносилен тому, что передан был сигнал ![]() , а значит, результатом обнаружения является двоичная единица. Подобным образом выбор
, а значит, результатом обнаружения является двоичная единица. Подобным образом выбор ![]() равносилен передаче сигнала
равносилен передаче сигнала ![]() , а значит, результатом обнаружения является двоичный нуль.
, а значит, результатом обнаружения является двоичный нуль.
3.1.3. Векторное представление сигналов и шума
Рассмотрим геометрическое или векторное представление, приемлемое как для узкополосных, так и полосовых сигналов. Определим N-мерное ортогональное пространство как пространство, определяемое набором N линейно независимых функций ![]() , именуемых базисными. Любая функция этого пространства может выражаться через линейную комбинацию базисных функций, которые должны удовлетворять условию
, именуемых базисными. Любая функция этого пространства может выражаться через линейную комбинацию базисных функций, которые должны удовлетворять условию
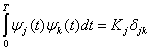
![]()
![]() (3.8, а)
(3.8, а)
где оператор
![]()
![]()
![]() (3.8, б)
(3.8, б)
называется дельта-функцией Кронекера и определяется формулой (3.8,б). При ненулевых константах ![]() пространство именуется ортогональным. Если базисные функции нормированы так, что все
пространство именуется ортогональным. Если базисные функции нормированы так, что все ![]() , пространство называется ортонормированным. Основное условие ортогональности можно сформулировать следующим образом: каждая функция
, пространство называется ортонормированным. Основное условие ортогональности можно сформулировать следующим образом: каждая функция ![]() набора базисных функций должна быть независимой от остальных функций набора. Каждая функция
набора базисных функций должна быть независимой от остальных функций набора. Каждая функция ![]() не должна интерферировать с другими функциями в процессе обнаружения. С геометрической точки зрения все функции
не должна интерферировать с другими функциями в процессе обнаружения. С геометрической точки зрения все функции ![]() взаимно перпендикулярны. Пример подобного пространства с N=3 показан на рис. 3.3, где взаимно перпендикулярные оси обозначены
взаимно перпендикулярны. Пример подобного пространства с N=3 показан на рис. 3.3, где взаимно перпендикулярные оси обозначены ![]() ,
, ![]() и
и ![]() . Если
. Если ![]() соответствует действительному компоненту напряжения или тока сигнала, нормированному на сопротивление 1 Ом, то, используя формулы (1.5) и (3.8), получаем следующее выражение для нормированной энергии в джоулях,
соответствует действительному компоненту напряжения или тока сигнала, нормированному на сопротивление 1 Ом, то, используя формулы (1.5) и (3.8), получаем следующее выражение для нормированной энергии в джоулях,
переносимой сигналом ![]() за Т секунд.
за Т секунд.
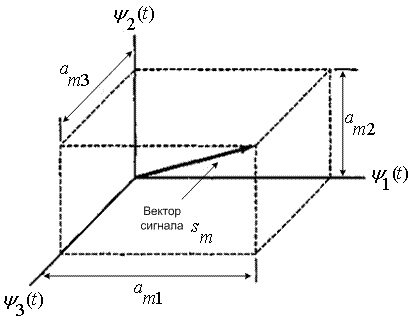
Рис. 3.3. Векторное представление сигнала ![]()
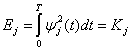 (3.9)
(3.9)
Одной из причин нашего внимания к ортогональному сигнальному пространству является то, что в нем проще всего определяется Евклидова мера расстояния, используемая в процессе обнаружения. Стоит отметить, что даже если волны, переносящие сигналы, не формируют подобного пространства, они могут преобразовываться в линейную комбинацию ортогональных сигналов. Можно показать [3], что произвольный конечный набор сигналов ![]()
![]() , где каждый элемент множества физически реализуем и имеет длительность Т, можно выразить как линейную комбинацию N ортогональных сигналов
, где каждый элемент множества физически реализуем и имеет длительность Т, можно выразить как линейную комбинацию N ортогональных сигналов ![]() ,
, ![]() ,...,
,..., ![]() , где
, где ![]() , так, что
, так, что
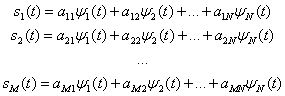
Эти соотношения можно записать в более компактной форме.
![]()
![]() (3.10)
(3.10)
![]() ,
,
где
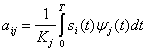
![]()
![]()
![]() (3.11)
(3.11)
![]() - это коэффициент при
- это коэффициент при ![]() разложения сигнала
разложения сигнала ![]() по базисным функциям. Вид базиса
по базисным функциям. Вид базиса ![]() не задается; эти сигналы выбираются с точки зрения удобства и зависят от формы волн передачи сигналов. Набор таких волн
не задается; эти сигналы выбираются с точки зрения удобства и зависят от формы волн передачи сигналов. Набор таких волн ![]() можно рассматривать как набор векторов
можно рассматривать как набор векторов ![]() . Если, например, N=3, то сигналу
. Если, например, N=3, то сигналу
![]() ,
,
соответствует вектор ![]() , который можно изобразить как точку в трехмерном Евклидовом пространстве с координатами
, который можно изобразить как точку в трехмерном Евклидовом пространстве с координатами ![]() , как показано на рис. 3.3. Взаимная ориентация векторов сигналов описывает связь между сигналами (относительно их фаз или частот), а амплитуда каждого вектора набора
, как показано на рис. 3.3. Взаимная ориентация векторов сигналов описывает связь между сигналами (относительно их фаз или частот), а амплитуда каждого вектора набора ![]() является мерой энергии сигнала, перенесенной в течение времени передачи символа. Вообще, после выбора набора из N ортогональных функций, каждый из переданных сигналов
является мерой энергии сигнала, перенесенной в течение времени передачи символа. Вообще, после выбора набора из N ортогональных функций, каждый из переданных сигналов ![]() полностью определяется вектором его коэффициентов.
полностью определяется вектором его коэффициентов.
![]()
![]() (3.12)
(3.12)
В дальнейшем для отображения сигналов в векторной форме будем использовать запись ![]() или
или ![]() . На рис. 3.4 в векторной форме (которая в данном случае является очень удобной) показан процесс обнаружения. Векторы
. На рис. 3.4 в векторной форме (которая в данном случае является очень удобной) показан процесс обнаружения. Векторы ![]() и
и ![]() представляют сигналы-прототипы, или опорные сигналы, принадлежащие набору из М сигналов,
представляют сигналы-прототипы, или опорные сигналы, принадлежащие набору из М сигналов, ![]() . Приемник априори знает местонахождение в пространстве сигналов всех векторов-прототипов, принадлежащих М-мерному множеству. В процессе передачи каждый сигнал подвергается воздействию шумов, так что в действительности принимается искаженная версия исходного сигнала (например,
. Приемник априори знает местонахождение в пространстве сигналов всех векторов-прототипов, принадлежащих М-мерному множеству. В процессе передачи каждый сигнал подвергается воздействию шумов, так что в действительности принимается искаженная версия исходного сигнала (например, ![]() или
или ![]() ), где
), где ![]() - вектор помех. Будем считать, что помехи являются аддитивными и имеют гауссово распределение; следовательно, результирующее распределение возможных принимаемых сигналов - это кластер или облако точек вокруг
- вектор помех. Будем считать, что помехи являются аддитивными и имеют гауссово распределение; следовательно, результирующее распределение возможных принимаемых сигналов - это кластер или облако точек вокруг ![]() и
и ![]() . Кластер сгущается к центру и разрежается с увеличением расстояния от прототипа. Стрелочка с пометкой «
. Кластер сгущается к центру и разрежается с увеличением расстояния от прототипа. Стрелочка с пометкой «![]() » представляет вектор сигнала, который поступает в приемник в течение определенного интервала передачи символа. Задача приемника - определить, на какой из прототипов М-мерного множества сигнал «похож» больше. Мерой «сходства» может быть расстояние. Приемник или детектор должен решить, какой из прототипов сигнального пространства ближе к принятому вектору
» представляет вектор сигнала, который поступает в приемник в течение определенного интервала передачи символа. Задача приемника - определить, на какой из прототипов М-мерного множества сигнал «похож» больше. Мерой «сходства» может быть расстояние. Приемник или детектор должен решить, какой из прототипов сигнального пространства ближе к принятому вектору ![]() . Анализ всех схем демодуляции или обнаружения включает использование понятия расстояние между принятым сигналом и набором возможных переданных сигналов. Детектор должен следовать одному простому правилу: определять
. Анализ всех схем демодуляции или обнаружения включает использование понятия расстояние между принятым сигналом и набором возможных переданных сигналов. Детектор должен следовать одному простому правилу: определять ![]() к тому же классу, к которому принадлежит его ближайший сосед (ближайший вектор-прототип).
к тому же классу, к которому принадлежит его ближайший сосед (ближайший вектор-прототип).
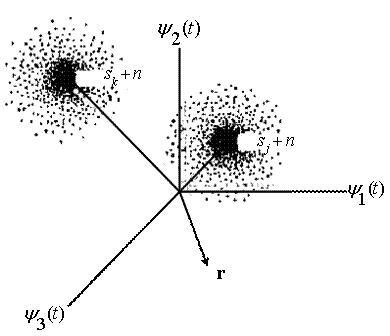
Рис.3.4. Сигналы и шум в трехмерном векторном пространстве
3.1.3.1. Энергия сигнала
С помощью формул (1.5), (3.10) и (3.8) нормированную энергию ![]() , связанную с сигналом
, связанную с сигналом ![]() в течение периода передачи символа Т, можно выразить через ортогональные компоненты
в течение периода передачи символа Т, можно выразить через ортогональные компоненты ![]() .
.
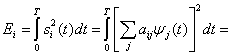 (3.13)
(3.13)
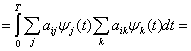 (3.14)
(3.14)
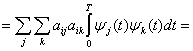 (3.15)
(3.15)
![]() (3.16)
(3.16)
![]()
![]() (3.17)
(3.17)
Уравнение (3.17) - это частный случай теоремы Парсеваля, связывающей интеграл от квадрата сигнала ![]() с суммой квадратов коэффициентов ортогонального разложения
с суммой квадратов коэффициентов ортогонального разложения ![]() . При использовании ортонормированных функций (т.е. при
. При использовании ортонормированных функций (т.е. при ![]() ) нормированная энергия за промежуток времени Т дается следующим выражением.
) нормированная энергия за промежуток времени Т дается следующим выражением.
![]() (3.18)
(3.18)
Если все сигналы ![]() имеют одинаковую энергию, формулу (3.18) можно записать следующим образом.
имеют одинаковую энергию, формулу (3.18) можно записать следующим образом.
3.1.3.2. Обобщенное преобразование Фурье
Преобразование, описанное формулами (3.8), (3.10) и (3.11), называется обобщенным преобразованием Фурье. При обычном преобразовании Фурье множество ![]() включает синусоиды и косинусоиды, а в случае обобщенного преобразования оно не ограничено какой-либо конкретной формой; это множество должно лишь удовлетворять условию ортогональности, записанному в форме уравнения (3.8). Обобщенное преобразование Фурье позволяет представить любой произвольный интегрируемый набор сигналов (или шумов) в виде линейной комбинации ортогональных сигналов [3]. Следовательно, в подобном ортогональном пространстве в качестве критерия принятия решения для обнаружения любого набора сигналов при шуме AWGN вполне оправдано использование расстояния (Евклидового расстояния). Вообще, важнейшее применение этого ортогонального преобразования связано с действительной передачей и приемом сигналов. Передача неортогонального набора сигналов в общем случае осуществляется посредством подходящего взвешивания ортогональных компонентов несущих.
включает синусоиды и косинусоиды, а в случае обобщенного преобразования оно не ограничено какой-либо конкретной формой; это множество должно лишь удовлетворять условию ортогональности, записанному в форме уравнения (3.8). Обобщенное преобразование Фурье позволяет представить любой произвольный интегрируемый набор сигналов (или шумов) в виде линейной комбинации ортогональных сигналов [3]. Следовательно, в подобном ортогональном пространстве в качестве критерия принятия решения для обнаружения любого набора сигналов при шуме AWGN вполне оправдано использование расстояния (Евклидового расстояния). Вообще, важнейшее применение этого ортогонального преобразования связано с действительной передачей и приемом сигналов. Передача неортогонального набора сигналов в общем случае осуществляется посредством подходящего взвешивания ортогональных компонентов несущих.
Пример 3.1. Ортогональное представление сигналов
На рис. 3.5 иллюстрируется утверждение, что любой произвольный интегрируемый набор сигналов может представляться как линейная комбинация ортогональных сигналов. На рис. 3.5, а показан набор из трех сигналов, ![]() ,
, ![]() и
и ![]() .
.
а) Покажите, что данные сигналы не взаимно ортогональны.
б) На рис. 3.5, б показаны два сигнала ![]() и
и ![]() . Докажите, что эти сигналы ортогональны.
. Докажите, что эти сигналы ортогональны.
в) Покажите, как неортогональные сигналы из п. а можно выразить как линейную комбинацию ортогональных сигналов из п. б.
г) На рис. 3.5, в показаны другие два сигнала ![]() и
и ![]() . Покажите, как неортогональные сигналы, показанные на рис. 3.5, а, выражаются через линейную комбинацию сигналов, изображенных на рис. 3.5, в.
. Покажите, как неортогональные сигналы, показанные на рис. 3.5, а, выражаются через линейную комбинацию сигналов, изображенных на рис. 3.5, в.
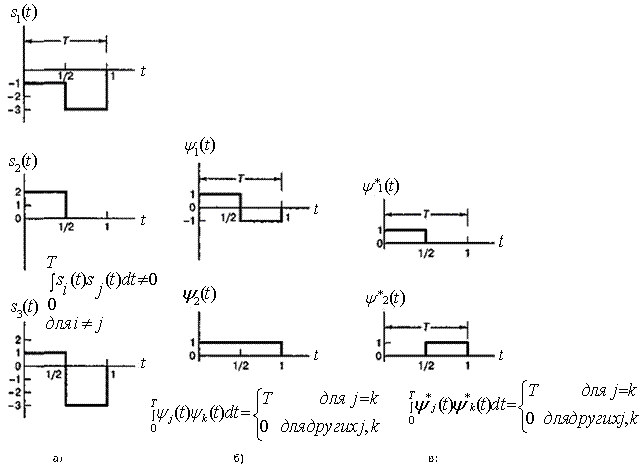
Рис. 3.5. Пример выражения произвольного набора сигналов через ортогональный набор: а) произвольный набор сигналов;
б) набор ортогональных базисных функций;
в) другой набор ортогональных базисных функций
Решение
а) Сигналы ![]() ,
, ![]() и
и ![]() , очевидно, не являются взаимно ортогональными, поскольку не удовлетворяют требованиям, указанным в формуле (3.8), т.е. интегрирование по времени (по периоду передачи символа) скалярного произведения любых двух из трех сигналов не равно нулю. Покажем это для сигналов
, очевидно, не являются взаимно ортогональными, поскольку не удовлетворяют требованиям, указанным в формуле (3.8), т.е. интегрирование по времени (по периоду передачи символа) скалярного произведения любых двух из трех сигналов не равно нулю. Покажем это для сигналов ![]() и
и ![]() .
.
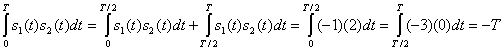
Подобным образом интегрирование по интервалу времени Т каждого из скалярных произведений ![]()
![]() и
и ![]()
![]() дает ненулевой результат. Следовательно, множество сигналов
дает ненулевой результат. Следовательно, множество сигналов ![]()
![]() на рис. 3.5, а не является ортогональным
на рис. 3.5, а не является ортогональным
б) Используя формулу (3.8), докажем, что ![]() и
и ![]() ортогональны.
ортогональны.
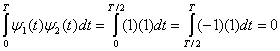
в) С использованием формулы (3.11) при ![]() , неортогональное множество сигналов
, неортогональное множество сигналов ![]()
![]() можно выразить через линейную комбинацию ортогональных базисных сигналов
можно выразить через линейную комбинацию ортогональных базисных сигналов ![]()
![]() .
.
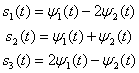
г) Подобно тому, как было сделано в п. в, неортогональное множество ![]()
![]() можно выразить через ортогональный набор базисных функций
можно выразить через ортогональный набор базисных функций ![]()
![]() , изображенный на рис. 3.5, в.
, изображенный на рис. 3.5, в.
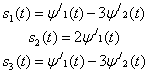
Эти соотношения показывают, как произвольный набор сигналов ![]() выражается через линейную комбинацию сигналов ортогонального набора
выражается через линейную комбинацию сигналов ортогонального набора ![]() , что описывается формулами (3.10) и (3.11). Какое практическое значение имеет возможность представления сигналов
, что описывается формулами (3.10) и (3.11). Какое практическое значение имеет возможность представления сигналов ![]()
![]() и
и ![]() через сигналы
через сигналы ![]() ,
, ![]() и соответствующие коэффициенты? Если мы хотим, чтобы система передавала сигналы
и соответствующие коэффициенты? Если мы хотим, чтобы система передавала сигналы ![]() ,
, ![]() и
и ![]() , достаточно, чтобы передатчик и приемник реализовывались только с использованием двух базисных функций
, достаточно, чтобы передатчик и приемник реализовывались только с использованием двух базисных функций ![]() и
и ![]() , а не трех исходных сигналов. Получить ортогональный набор базисных функций
, а не трех исходных сигналов. Получить ортогональный набор базисных функций ![]() из любого данного набора сигналов
из любого данного набора сигналов ![]() позволяет процесс ортогонализации Грамма-Шмидта. (Подробно этот процесс описан в приложении 4А работы [4].) .
позволяет процесс ортогонализации Грамма-Шмидта. (Подробно этот процесс описан в приложении 4А работы [4].) .
3.1.3.3. Представление белого шума через ортогональные сигналы
Аддитивный белый гауссов шум (additive white Gaussian noise - AWGN), как и любой другой сигнал, можно выразить как линейную комбинацию ортогональных сигналов. Для последующего рассмотрения процесса обнаружения сигналов шум удобно разделить на два компонента:
![]() , (3.20)
, (3.20)
где
![]() (3.21)
(3.21)
является шумом в пространстве сигналов или проекцией компонентов шума на координаты сигнала ![]() , a
, a
![]() (3.22)
(3.22)
есть шумом вне пространства сигналов. Другими словами, ![]() можно рассматривать как шум, эффективно отсеиваемый детектором, a
можно рассматривать как шум, эффективно отсеиваемый детектором, a ![]() - как шум, который будет «вмешиваться» в процесс обнаружения. Итак, сигнал шума
- как шум, который будет «вмешиваться» в процесс обнаружения. Итак, сигнал шума ![]() можно выразить следующим образом.
можно выразить следующим образом.
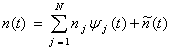 (3.23)
(3.23)
где
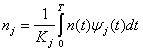 для всех
для всех ![]() (3.24)
(3.24)
и
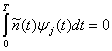 для всех
для всех ![]() (3.25)
(3.25)
Компонент ![]() шума, выраженный в формуле (3.21), следовательно, можно считать просто равным
шума, выраженный в формуле (3.21), следовательно, можно считать просто равным ![]() . Выразить шум
. Выразить шум ![]() можно через вектор его коэффициентов, подобно тому, как это делалось для сигналов в формуле (3.12). Имеем
можно через вектор его коэффициентов, подобно тому, как это делалось для сигналов в формуле (3.12). Имеем
![]() , (3.26)
, (3.26)
где ![]() - случайный вектор с нулевым средним и гауссовым распределением, а компоненты шума
- случайный вектор с нулевым средним и гауссовым распределением, а компоненты шума ![]() ,
, ![]() являются независимыми.
являются независимыми.
3.1.3.4. Дисперсия белого шума
Белый шум - это идеализированный процесс с двусторонней спектральной плотностью мощности, равной постоянной величине ![]() для всех частот от
для всех частот от ![]() до
до ![]() . Следовательно, дисперсия шума (средняя мощность шума, поскольку шум имеет нулевое среднее) равна следующему.
. Следовательно, дисперсия шума (средняя мощность шума, поскольку шум имеет нулевое среднее) равна следующему.
![]() (3.27)
(3.27)
Хотя дисперсия AWGN равна бесконечности, дисперсия фильтрованного шума AWGN конечна. Например, если AWGN коррелирует с одной из набора ортонормированных функций ![]() , дисперсия на выходе коррелятора описывается следующим выражением.
, дисперсия на выходе коррелятора описывается следующим выражением.
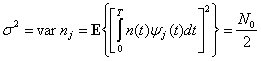 (3.28)
(3.28)
Доказательство формулы (3.28) приводится в приложении В. С этого момента будем считать, что интересующий нас шум процесса обнаружения является шумом на выходе коррелятора или согласованного фильтра с дисперсией ![]() , как указано в формуле (3.28).
, как указано в формуле (3.28).
3.1.4. Важнейший параметр систем цифровой связи - отношение сигнал/шум
Любой, кто изучал аналоговую связь, знаком с критерием качества, именуемым отношением средней мощности сигнала к средней мощности шума (S/N или SNR). В цифровой связи в качестве критерия качества чаще используется нормированная версия SNR, ![]() .
. ![]() - это энергия бита, и ее можно описать как мощность сигнала S, умноженную на время передачи бита
- это энергия бита, и ее можно описать как мощность сигнала S, умноженную на время передачи бита ![]() .
. ![]() - это спектральная плотность мощности шума, и ее можно выразить как мощность шума N, деленную на ширину полосы W. Поскольку время передачи бита и скорость передачи битов
- это спектральная плотность мощности шума, и ее можно выразить как мощность шума N, деленную на ширину полосы W. Поскольку время передачи бита и скорость передачи битов ![]() , взаимно обратны,
, взаимно обратны, ![]() можно заменить на
можно заменить на ![]() .
.
![]() (3.29)
(3.29)
Еще одним параметром, часто используемым в цифровой связи, является скорость передачи данных в битах в секунду. В целях упрощения выражений, встречающихся в книге, для представления скорости передачи битов вместо записи ![]() будем писать просто R. С учетом сказанного перепишем, выражение (3,29) так, чтобы было явно видно, что отношение
будем писать просто R. С учетом сказанного перепишем, выражение (3,29) так, чтобы было явно видно, что отношение ![]() представляет собой отношение S/N, нормированное на ширину полосы и скорость передачи битов.
представляет собой отношение S/N, нормированное на ширину полосы и скорость передачи битов.
![]() (3.30)
(3.30)
Одной из важнейших метрик производительности в системах цифровой связи является график зависимости вероятности появления ошибочного бита ![]() от
от ![]() . На рис. 3.6 показан «водопадоподобный» вид большинства подобных кривых. При
. На рис. 3.6 показан «водопадоподобный» вид большинства подобных кривых. При ![]() ,
, ![]() . Безразмерное отношение
. Безразмерное отношение ![]() - это стандартная качественная мера производительности систем цифровой связи. Следовательно, необходимое отношение
- это стандартная качественная мера производительности систем цифровой связи. Следовательно, необходимое отношение ![]() можно рассматривать как метрику, позволяющую сравнивать производительность различных систем; чем меньше требуемое отношение
можно рассматривать как метрику, позволяющую сравнивать производительность различных систем; чем меньше требуемое отношение ![]() , тем эффективнее процесс обнаружения при данной вероятности ошибки.
, тем эффективнее процесс обнаружения при данной вероятности ошибки.
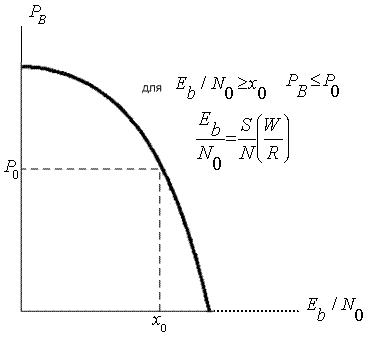
Рис. 3.6. Общий вид зависимости ![]() от
от ![]() .
.
3.1.5. Почему отношение 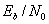 - это естественный критерий качества
- это естественный критерий качества
У неспециалистов в области цифровой связи может возникнуть вопрос о полезности параметра ![]() . Отношение S/N - это удобный критерий качества для аналоговых систем связи: числитель представляет меру мощности сигнала, которую желательно сохранить, а знаменатель - ухудшение вследствие электрических помех. Более того, отношение S/N интуитивно воспринимается как мера качества. Итак, почему в цифровых системах связи мы не можем продолжать использовать отношение S/N как критерий качества? Зачем для цифровых систем нужна другая метрика - отношение энергии бита к спектральной плотности мощности шума? Объяснению этого вопроса и посвящен данный раздел.
. Отношение S/N - это удобный критерий качества для аналоговых систем связи: числитель представляет меру мощности сигнала, которую желательно сохранить, а знаменатель - ухудшение вследствие электрических помех. Более того, отношение S/N интуитивно воспринимается как мера качества. Итак, почему в цифровых системах связи мы не можем продолжать использовать отношение S/N как критерий качества? Зачем для цифровых систем нужна другая метрика - отношение энергии бита к спектральной плотности мощности шума? Объяснению этого вопроса и посвящен данный раздел.
В разделе 1.2.4 сигнал в представлении через мощность определялся как сигнал с конечной средней мощностью и бесконечной энергией. Энергетический сигнал определялся как сигнал с нулевой средней мощностью и конечной энергией. Подобная классификация полезна при сравнении аналоговых и цифровых сигналов. Аналоговый сигнал мы относим к сигналам, представляемым через мощность. Почему это имеет смысл? Об аналоговом сигнале можно думать как о сигнале, имеющем бесконечную длительность, который не требуется разграничивать во времени. Неограниченно длительный аналоговый сигнал содержит бесконечную энергию; следовательно, использование энергии - это не самый удобный способ описания характеристик такого сигнала. Значительно более удобным параметром для аналоговых волн является мощность (или скорость доставки энергии).
В то же время в системах цифровой связи мы передаем (и принимаем) символы путем передачи некоторого сигнала в течение конечного промежутка времени, времени передачи символа ![]() . Сконцентрировав внимание на одном символе, видим, что мощность (усредненная по времени) стремится к нулю. Значит, для описания характеристик цифрового сигнала мощность не подходит. Для подобного сигнала нам нужна метрика, «достаточно хорошая» в пределах конечного промежутка времени. Другими словами, энергия символа (мощность, проинтегрированная по
. Сконцентрировав внимание на одном символе, видим, что мощность (усредненная по времени) стремится к нулю. Значит, для описания характеристик цифрового сигнала мощность не подходит. Для подобного сигнала нам нужна метрика, «достаточно хорошая» в пределах конечного промежутка времени. Другими словами, энергия символа (мощность, проинтегрированная по ![]() ) - это гораздо более удобный параметр описания цифровых сигналов.
) - это гораздо более удобный параметр описания цифровых сигналов.
То, что цифровой сигнал лучше всего характеризует полученная им энергия, еще не дает ответа на вопрос, почему ![]() - это естественная метрика для цифровых систем, так что продолжим. Цифровой сигнал - это транспортное средство, представляющее цифровое сообщение. Сообщение может содержать один бит (двоичное сообщение), два (четверичное),..., 10 бит (1024-ричное). В аналоговых системах нет ничего подобного такой дискретной структуре сообщения. Аналоговый информационный источник - это бесконечно квантованная непрерывная волна. Для цифровых систем критерий качества должен позволять сравнивать одну систему с другой на битовом уровне. Следовательно, описывать цифровые сигналы в терминах S/N практически бесполезно, поскольку сигнал может иметь однобитовое, 2-битовое или 10-битовое значение. Предположим, что для данной вероятности возникновения ошибки в цифровом двоичном сигнале требуемое отношение S/N равно 20. Будем считать, что понятия сигнала и его значения взаимозаменяемы. Поскольку двоичный сигнал имеет однобитовое значение, требуемое отношение S/N на бит равно 20 единицам. Предположим, что наш сигнал является 1024-ричным, с теми же 20 единицами требуемого отношения S/N. Теперь, поскольку сигнал имеет 10-битовое значение, требуемое отношение S/N на один бит равно всего 2. Возникает вопрос: почему мы должны выполнять такую цепочку вычислений, чтобы найти метрику, представляющую критерий качества? Почему бы сразу не выразить метрику через то, что нам действительно надо, - параметр, связанный с энергией на битовом уровне,
- это естественная метрика для цифровых систем, так что продолжим. Цифровой сигнал - это транспортное средство, представляющее цифровое сообщение. Сообщение может содержать один бит (двоичное сообщение), два (четверичное),..., 10 бит (1024-ричное). В аналоговых системах нет ничего подобного такой дискретной структуре сообщения. Аналоговый информационный источник - это бесконечно квантованная непрерывная волна. Для цифровых систем критерий качества должен позволять сравнивать одну систему с другой на битовом уровне. Следовательно, описывать цифровые сигналы в терминах S/N практически бесполезно, поскольку сигнал может иметь однобитовое, 2-битовое или 10-битовое значение. Предположим, что для данной вероятности возникновения ошибки в цифровом двоичном сигнале требуемое отношение S/N равно 20. Будем считать, что понятия сигнала и его значения взаимозаменяемы. Поскольку двоичный сигнал имеет однобитовое значение, требуемое отношение S/N на бит равно 20 единицам. Предположим, что наш сигнал является 1024-ричным, с теми же 20 единицами требуемого отношения S/N. Теперь, поскольку сигнал имеет 10-битовое значение, требуемое отношение S/N на один бит равно всего 2. Возникает вопрос: почему мы должны выполнять такую цепочку вычислений, чтобы найти метрику, представляющую критерий качества? Почему бы сразу не выразить метрику через то, что нам действительно надо, - параметр, связанный с энергией на битовом уровне, ![]() ? В заключение отметим, что поскольку отношение S/N является безразмерным, таким же есть и отношение
? В заключение отметим, что поскольку отношение S/N является безразмерным, таким же есть и отношение ![]() . Для проверки можно вычислить единицы измерения.
. Для проверки можно вычислить единицы измерения.
![]()

