8.4. Турбокоды

Категория: 8. Канальное кодирование: часть 3

8.4.1. Понятия турбокодирования

8.4.1.1. Функции правдоподобия

8.4.1.2. Пример класса из двух сигналов

8.4.1.3. Логарифмическое отношение правдоподобий

8.4.1.4. Принципы итеративного (турбо) декодирования

8.4.2. Алгебра логарифма правдоподобия

8.4.3. Пример композиционного кода

8.4.3.1. Пример двухмерного кода с одним разрядом контроля четности

8.4.3.2. Внешние правдоподобия

8.4.3.3. Вычисление внешних правдоподобий

8.4.4. Кодирование с помощью рекурсивного систематического кода

8.4.4.1. Конкатенация кодов RSC

8.4.5. Декодер с обратной связью

8.4.5.1. Декодирование при наличии контура обратной связи

8.4.5.2. Достоверность передачи при турбокодировании

8.4.6. Алгоритм MAP

8.4.6.1. Метрики состояний и метрика ветви

8.4.6.2. Расчет прямой метрики состояния

8.4.6.3. Расчет обратной метрики состояния

8.4.6.4. Расчет метрики ветви

8.4.7. Пример декодирования по алгоритму MAP

8.4.7.1. Расчет метрик ветвей

8.4.7.2. Расчет метрик состояний

8.4.7.3. Расчет логарифмического отношения правдоподобий

8.4.7.4. Реализация конечного автомата с помощью регистра сдвига

Схема каскадкого кодирования впервые была предложена Форни [16] как метод получения высокоэффективного кода посредством комбинацйи двух или более компонуемых кодов (иногда называемых составными). В результате, такие коды могут корректировать ошибки в значительно более длинных кодах и имеют структуру, которая позволяет относительно легко осуществить декодирование средней сложности. Последовательные каскадные коды часто используются в системах с ограничением мощности, таких как космические зонды. Самая распространенная из этих схем содержит внешний код Рида-Соломона (выполняется первым, убирается последним), который следует за сверточным внутренним кодом (выполняется последним, убирается первым) [10]. Турбокод можно считать обновлением структуры каскадного кодирования с итеративным алгоритмом декодирования связанной кодовой последовательности. Поскольку такая схема имеет итеративную форму, на рис. 1.3 турбокодирование представлено как отдельная категория в структурированных последовательностях.

Турбокоды впервые были введены в 1993 году Берру, Главье и Цитимаджимой (Berrou, Glavieux, Thitimajshima) и опубликованы в [17, 18], где в описываемой схеме достигалась вероятность появления ошибок при степени кодирования 1/2 и модуляции BPSK в канале с белым аддитивным гауссовым шумом (additive white Gaussian noise — AWGN) с , равным 0,7 дБ. Коды образуются посредством компоновки двух или более составных кодов, являющихся разными вариантами чередования одной и той же информационной последовательности. Тогда как для сверточных кодов на финальном этапе декодер выдает жестко декодированные биты (или в более общем случае — декодированные символы), в каскадной схеме, такой как турбоход, для хорошей работы алгоритм декодирования не должен ограничивать себя, подавая на декодеры жесткую схему решений. Для лучшего использования информации, получаемой с каждого декодера, алгоритм декодирования должен применять, в первую очередь, мягкую схему декодирования, вместо жесткой. Для систем с двумя составными кодами концепция, лежащая в основе турбодекодирования, заключается в том, чтобы передать мягкую схему принятия решений с выхода одного декодера на вход другого и повторять эту процедуру до тех пор, пока не будут получены надежные решения.

8.4.1. Понятия турбокодирования

8.4.1.1. Функции правдоподобия

Математическое обоснование критерия проверки гипотез остается за теоремой Байеса, которая приводится в приложении Б. В области связи, где наибольший интерес представляют прикладные системы, включающие в себя каналы AWGN, наиболее распространенной формой теоремы Байеса является та, которая выражает апостериорную вероятность (a posteriori probability— APP) решения через случайную непрерывную переменную х как

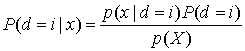
(8.61)

, (8.62)

где — это апостериорная вероятность, a d = i представляет данные d, принадлежащие i-му классу сигналов из набора классов М. Ранее представляло функцию плотности вероятности принимаемого непрерывного сигнала с шумом х, при d = i. Также , называемое априорной вероятностью, означает вероятность появления i-го класса сигналов. Обычно х представляет "наблюдаемую" случайную переменную или лежащую в основе критерия статистику, которая получается на выходе, демодулятора или какого-либо иного устройства обработки сигналов. Поэтому p(х) — это функция распределения вероятностей принятого сигнала х, дающая тестовую статистику в полном пространстве классов сигналов. В уравнении (8.61) при конкретном наблюдении p(x) является коэффициентом масштабирования, поскольку он получается путем усреднения по всем классам пространства. Литера p нижнего регистра используется для обозначения функции распределения вероятностей непрерывной случайной переменной, а литера P верхнего регистра — для обозначения вероятности (априорной и апостериорной). Определение апостериорной вероятности принятого сигнала, из уравнения (8.61), можно представлять как результат эксперимента. Перед экспериментом, в общем, существует (или поддается оценке) априорная вероятность . В эксперименте для расчета апостериорной вероятности, используется уравнение (8.61), и это можно считать "обновлением" имевшихся сведений, полученных при изучении принятого сигнала х.

8.4.1.2. Пример класса из двух сигналов

Пусть двоичные логические элементы 1 и 0 представляются электрическими напряжениями +1 и -1. Переменная d представляет бит переданных данных, который выглядит как уровень напряжения или логический элемент. Иногда более предпочтительным оказывается один из способов представления; читатель должен уметь различать это по контексту. Пусть двоичный 0 (или электрическое напряжение -1) будет нулевым элементом при сложении. На рис. 8.20 показана условная функция распределения вероятностей при передаче сигнала по каналу AWGN, представленная как функция правдоподобия. Функция, изображенная справа, , представляет функцию распределения вероятностей случайной переменной х, которая передается при условии, что . Функция, изображенная слева, , в свою очередь, представляет ту же функцию распределения вероятностей случайной переменной х, которая передается при условии, что . На оси абсцисс показан полный диапазон возможных значений тестовой статистики х, которая образуется в приемнике. На рис. 8.20 показано одно такое произвольное значение , индекс которого представляет наблюдение, произведенное в k-й период времени. Прямая, опушенная в точку , пересекает две кривые функций правдоподобия, что дает в итоге два значения правдоподобия и . Хорошо известное правило принятия решения по жесткой схеме, называемое принципом максимального правдоподобия, определяет выбор данных или , основываясь на большем из двух имеющихся значений или . Для каждого бита данных в момент k решение гласит, что , если попадает по правую сторону линии принятия решений, обозначаемой , в противном случае — .

Аналогичное правило принятия решения, известное как максимум апостериорной вероятности (maximum a posteriori — MAP), можно представить в виде правила минимальной вероятности ошибки, принимая во внимание априорную вероятность данных. В общем случае правило MAP выражается следующим образом.

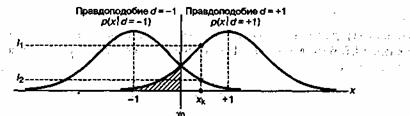
Рис. 8.20. Функции правдоподобия

Я. 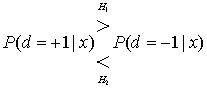(8.63)

Уравнение (8.63) утверждает, что выбирается одна из гипотез — , если апостериорная вероятность больше апостериорной вероятности . В противном случае выбирается гипотеза , . Воспользовавшись байесовской формой уравнения (8.61), можно заменить апостериорную вероятность в уравнении (8.63) эквивалентным выражением, что дает следующее.

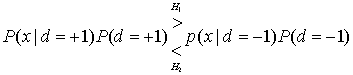(8.64)

Здесь функция распределения вероятности p(х), имеющаяся в обеих частях неравенства, (8.61), была исключена. Уравнение (8.64), в целом представленное через дроби, дает так называемую проверку отношения правдоподобий.

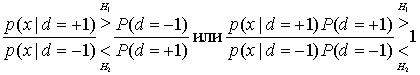(8.65)

8.4.1.3. Логарифмическое отношение правдоподобий

Если взять логарифм от соотношения правдоподобия, полученного в уравнениях (8.63)-(8.65), получится удобная во многих отношениях метрика, называемая логарифмическое отношение правдоподобия (log-likelihood ratio — LLR). Это вещественное представление мягкого решения вне декодера определяется выражением

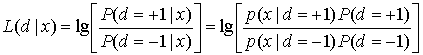(8.66)

так, что

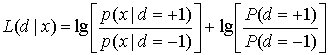(8.67)

или

, (8.68)

где — это LLR тестовой статистики х, получаемой путем измерений х на выходе канала при чередовании условий, что может быть передан или ,a L(d) — априорное LLR бита данных d. Для упрощения обозначений уравнение (8.68) можно переписать следующим образом.

(8.69)

Здесь означает, что данный член LLR получается в результате канальных измерений, произведенных в приемнике. Уравнения (8.61)—(8.69) получены только исходя из данных детектора. Далее введение декодера даст стандартные преимущества схемы принятия решений. Для систематических кодов было пЬказано [17], что LLR (мягкий выход) вне декодера равняется следующему.

(8.70)

Здесь — это LLR бита данных вне демодулятора (на входе декодера), а называется внешним LLR и представляет внешнюю информацию, вытекающую из процесса декодирования. Выходная последовательность систематического декодера образована величинами, представляющими информационные биты или биты четности. Из уравнений (8.69) и (8.70) выходное LLR декодера теперь примет следующий вид.

(8.71)

Уравнение (8.71) показывает, что выходное LLR систематического декодера можно представить как состоящее из трех компонентов — канального измерения, априорного знания данных и внешнего LLR, относящегося только к декодеру. Чтобы получить финальное , нужно просуммировать отдельные вклады LLR, как показано в уравнении (8.71), поскольку все три компонента статистически независимы [17, 19]. Доказательство оставляем читателю в качестве самостоятельного упражнения (см. задачу 8.18.). Мягкий выход декодера является вещественным числом, обеспечивающим в итоге как само принятие жесткого решения, так и его надежность. Знак задает жесткое решение, т.е. при положительном знаке решение — , а при отрицательном — . Величина определяет надежность этого решения. Часто величина вследствие декодирования имеет тот же знак, что и , и поэтому повышает надежность .

8.4.1.4. Принципы итеративного (турбо) декодирования

В типичном приемнике демодулятор часто разрабатывается для выработки решений по мягкой схеме, которые затем будут переданы на декодер. В главе 7 повышение достоверности передачи в системе, по сравнению с жесткой схемой принятия решений, оценивается приблизительно в 2 дБ в канале AWGN. Такой декодер следует называть декодером с мягким входом и жестким выходом, поскольку процесс финального декодирования должен завершаться битами (жесткая схема). В турбокодах, где используется два или несколько составных кодов и декодирование подразумевает подключение выхода одного декодера ко входу другого для возможности поддержки итераций, декодер с жестким выходом нежелателен. Это связано с тем, что жесткая схема в декодере снизит производительность системы (по сравнению с мягкой схемой). Следовательно, для реализации турбодекодирования необходим декодер с мягким входом и мягким выходом. Во время перво итерации на таком декодере (с мягким входом и мягким выходом), показанном на рис. 8.21, данные считаются равновероятными, что дает начальное априорное значение LLR для третьего члена уравнения (8.67). Канальное значение LLR Lc(x) получается путем взятия логарифма отношения величин и для определенных значений х (рис. 8.20) и является вторым членом уравнения (8.67). Выход декодера на рис. 8.21 образуется из LLR детектора и внешнего LLR выхода и представляет собой сведения, вытекающие из процесса декодирования. Как показано на рис. 8.21 для итеративного декодирования, внешнее правдоподобие подается обратно на вход (иного составного декодера) для обновления априорной вероятности информации следующей итерации.

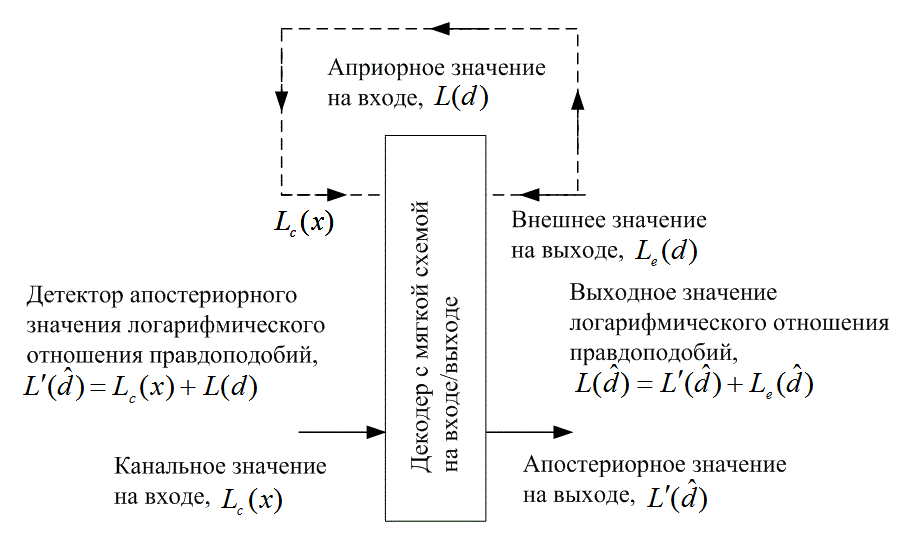
Рис. 8.21. Декодер с мягким входом и мягким выходом

8.4.2. Алгебра логарифма правдоподобия

Для более подробного объяснения итеративной обратной связи выходов мягких декодеров, вводится понятие алгебры логарифма правдоподобия [19]. Для статистически независимых данных d сумма двух логарифмических отношений правдоподобия (log-likelihood ratio — LLR) определяется следующим образом.

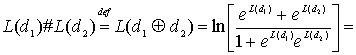(8.72)

(8.72)

Здесь использован натуральный логарифм, а функция возвращает знак своего аргумента. В уравнении (8.72) имеется три операции сложения. Знак "" применяется для обозначения суммы по модулю 2 данных, представленных двоичными цифрами. Знак # используется для обозначения суммы логарифмов правдоподобия или, что то же самое, математической операции, описываемой уравнением (8.72). Сумма двух LLR обозначается оператором, который определяется как LLR суммы по модулю 2 основных статистически независимых информационных битов. Вывод уравнения (8.72) показан в приложении 8А. Уравнение (8.73) является аппроксимацией уравнения (8.72), которая будет использована позднее в численном примере. Сложение LLR, определяемое уравнениями (8.72) и (8.73), дает один очень интересный результат в том случае, если один из LLR значительно превышает второй.

Следует сказать, что алгебра логарифма правдоподобия, описанная здесь, немного отличается от той, которая используется в [19], из-за различного выбора нулевого элемента. В данном случае нулевым элементом двоичного набора (1, 0) выбран 0.

8.4.3. Пример композиционного кода

Рассмотрим двухмерный код (композиционный код), изображенный на рис. 8.22. Его структуру можно описать как массив данных, состоящий из строк и столбцов. В строках содержатся кодовые слова, образованные битами данных и битами четности. Каждая из строк представляет собой кодовое слово кода . Аналогично столбцов содержат кодовые слова, образованные из бит данных и бит четности. Таким образом, каждый из столбцов представляет собой кодовые слова кода . Различные участки структуры обозначены следующим образом: d — для данных, — для горизонтальной четности (вдоль строк) и — для вертикальной четности (вдоль столбцов). Фактически каждый блок битов данных размером кодирован двумя кодами — горизонтальным и вертикальным.

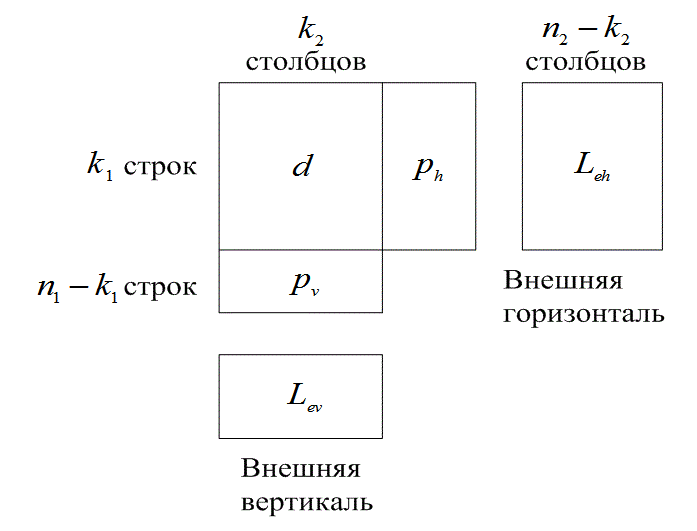
Рис. 8.22. Структура двухмерного композиционного кода

Еще на рис. 8.22 присутствуют блоки и , содержащие значения внешних LLR, полученные из горизонтального и вертикального кодов. Код с коррекцией ошибок дает некоторое улучшение достоверности передачи. Можно увидеть, что внешние LLR представляют собой меру этого улучшения. Заметьте, что такой композиционный код является простым примером каскадного кода. Его структура описывается двумя отдельными этапами кодирования — горизонтальным и вертикальным.

Напомним, что решение при финальном декодировании каждого бита и его надежности зависит от значения , как показывает уравнение (8.71). Опираясь на это уравнение, можно описать алгоритм, дающий внешние LLR (горизонтальное и вертикальное) и финальное . Для композиционного кода алгоритм такого итеративного декодирования будет иметь следующий вид.

1. Устанавливается априорное LLR (если априорные вероятности битов данных не равны).

2. Декодируется горизонтальный код и, основываясь на уравнении (8.71), вычисляется горизонтальное LLR.

3. .На этапе 4 вертикального декодирования устанавливается .

4. Декодируется вертикальный код и, основываясь на уравнении (8.71), вычисляется вертикальное LLR.

5. Для этапа 2 горизонтального декодирования устанавливается Затем повторяются этапы 2—5.

6. После достаточного для получения надежного решения количества итераций (т.е. повторения этапов 2-5) следует перейти к этапу 7.

7. Мягким решением на выходе будет

(8.74)

Далее следует пример, демонстрирующий применение этого алгоритма к очень простому композиционному коду.

8.4.3.1. Пример двухмерного кода с одним разрядом контроля четности

Пусть в кодере биты данных и биты контроля четности имеют значения, показанные на рис. 8.23, а. Связь между битами данных и битами контроля четности внутри конкретной строки (или столбца) выражается через двоичные цифры (1, 0) следующим образом.

Рис. 8.23. Пример композиционного кода

(8.75)

и

(8.76)

Здесь символ "" обозначает сумму по модулю 2. Переданные биты представлены последовательностью . На входе приемника искаженные помехами биты представляются последовательностью , . В данной ситуации для каждого принятого бита данных , для каждого принятого бита контроля четности , а n представляет собой распределение помех, которое статистически независимо от , и .Индексы i и j обозначают позицию в выходном массиве кодера, изображенном на рис. 8.23, а. Хотя зачастую удобнее использовать обозначение принятой последовательности в виде , где k является временным индексом. Оба типа обозначений будут рассматриваться далее; i и j используются для позиционных отношений внутри композиционного кода, a k — для более общих аспектов временной зависимости сигнала. Какое из обозначений должно быть заметно по контексту? Если основываться на отношениях, установленных в уравнениях (8.67)-(8.69), и считать модель каналом AWGN с помехами, LLR для канальных измерений сигнала принятого в момент k, будет иметь следующий вид.

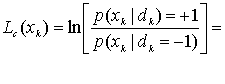(8.77,а)

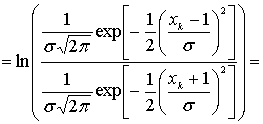(8.78,б)

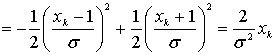(8.79,в)

Здесь применяется натуральный логарифм. Если сделать предварительное допущение, что помеха имеет дисперсию , равную 1, то получим следующее.

(8.78)

Рассмотрим пример, в котором информационная последовательность образована двоичными числами 1 0 0 1, как показано на рис. 8.23, а. Опираясь на уравнение (8.75), можно видеть, что контрольная последовательность должна быть равна 1 1 1 1. Следовательно, переданная последовательность будет иметь следующий вид.

(8.79)

Если информационные биты выражаются через значения биполярного э лектрического напряжения +1 и -1, соответствующие логическим двоичным уровням 1 и 0, то переданная последовательность будет следующей.

Допустим теперь, что помехи преобразуют эту последовательность информации и I контрольных данных в принятую последовательность

0,75, 0,05, 0,10, 0,15, 1,25, 1,0, 3,0, 0,5, (8.80)

где компоненты указывают переданную информацию и контрольные данные . Таким образом, следуя позиционному описанию, принятую последовательность можно записать следующим образом.

Из уравнения (8.78) предполагаемые канальные измерения дают следующие значения LLR.

1,5, 0,1, 0,20, 0,3, 2,5 ,2,0, 6,0, 1,0 (8.81)

Эти величины показаны на рис. 8.23, б как входные измерения декодера. Следует заметить, что (при равной априорной вероятности переданных данных) если принимаются жесткие решения на основе значений или описанных ранее, то такой процесс должен в результате давать две ошибки, поскольку и и могут быть неправильно трактованы как двоичная 1.

8.4.3.2. Внешние правдоподобия

В случае композиционного кода, изображенного на рис. 8.23, при выражении мягкого выхода для принятого сигнала, соответствующего данным , используется уравнение (8.71), так что

, (8.82)

где член представляют внешнее LLR, распределенное кодом (т.е. прием соответствующих данных и их априорной вероятности совместно с приемом соответствующей четности ). В общем случае мягким выходом для принятого сигнала, соответствующего данным будет

. (8.83)

где и — канальное измерение LLR приема соответствующих , и . , —LLR для априорных вероятностей и , — внешнее распределение LLR для кода. Уравнения (8.82) и (8.83) становятся понятнее при рассмотрении рис. 8.23, б. В данной ситуации, если считать, что происходит равновероятная передача сигнала, мягкий выход представляется измерением LLR детектора для приема, соответствующего данным , плюс внешнее LLR , получаемое в результате того, что данные и четность также дают сведения о данных , как это показывают уравнения (8.75) и (8.76).

8.4.3.3. Вычисление внешних правдоподобий

Для случая, показанного на рис. 8.23, горизонтальная часть расчетов для, получения Leh (d) и вертикальная часть расчетов для получения Lev (d) выглядят следующим образом.

(8.84,а)

(8.84,б)

(8.85,а)

(8.85,б)

(8.86,а)

(8.86,б)

(8.87,а)

(8.87,б)

Значения LLR, показанные на рис. 8.23, входят в выражение для в уравнениях (8.84)—(8.87). Подразумевая передачу сигналов равновероятной, а начальную установку значения равной нулю, получаем следующее.

- новое (8.88)

- новое (8.89)

- новое (8.90)

- новое (8.91)

где сложения логарифма правдоподобия производятся, исходя из приближения, показанного в уравнении (8.73). Далее, продолжая первое вертикальное вычисление, используются выражения для из уравнений (8.84)-(8.87). Теперь значение можно обновить, исходя из нового значения , полученного из первого вертикального вычисления, показанного в уравнениях (8.88)-(8.91).

- новое (8.92)

- новое (8.93)

- новое (8.94)

- новое (8.95)

Результаты первой полной итерации двух этапов декодирования (горизонтального и вертикального) будут следующими.

Исходные измерения

1,5

0,1

0,2

0,3

-0,1

-1,5

-0,3

-0,2

после первого вертикального декодирования

0

-1,6

-1,3

1,2

после первого вертикального декодирования

Каждый этап декодирования улучшает исходные LLR, которые основываются только на канальных измерениях. Это видно из расчетов выходного LLR декодера с помощью уравнения (8.74). Исходное LLR и внешние горизонтальные LLR вместе дают следующее улучшение (внешний вертикальный член еще не рассматривался).

Улучшение LLRиз-за

1,4

-1,4

-0,1

0,1

Исходное LLR совместно с горизонтальным и вертикальным внешним LLR дает следующее улучшение.

Улучшение LLR из-за

1,5

-1,5

-1,5

1,1

В данном случае можно видеть, что сведений, полученных лишь из горизонтального декодирования, достаточно для получения правильного жесткого решения вне декодера, но с низкой степенью доверия к битам данных d3 и d4. После включения внешних вертикальных LLR в декодер новые значения LLR появляются на более высоком уровне надежности и доверия. Пусть будет произведена еще одна вертикальная и одна горизонтальная итерация декодирования, чтобы определить наличие или отсутствие существенных изменений в результатах. Снова на помощь приходят отношения из уравнений (8.84)—(8.87), и далее следует горизонтальное вычисление для получения Leh(d) с новым L(d) из первого вертикального расчета, показанного в уравнениях (8.92)—(8.95), так что получаем следующее.

- новое (8.96)

- новое (8.97)

- новое (8.98)

- новое (8.99)

Затем необходимо выполнить второе вертикальное вычисление для получения с новым , полученным из второго горизонтального расчета, показанного в уравнения (8.96)-(8.99), что приводит к следующему.

- новое (8.100)

- новое (8.101)

- новое (8.102)

- ново е (8.103)

Вторая итерация вертикального и горизонтального декодирования, дающая упомянутые выше величины, отражается на мягких выходных LLR, которые снова рассчитываются из уравнения (8.74), переписанного сдедующим образом.

(8.104)

Горизонтальные и вертикальные LLR из уравнения (8.96)-(8.103) и итоговое LLR декодера показаны ниже. В данном примере вторые итерации, горизонтальная и вертикальная, что в целом дает всего четыре итерации, показывают скромный прирост, по сравнению с одной вертикальной и горизонтальной итерацией. Результаты показывают, что доверительные значения сохраняются для каждого из четырех данных.

Исходные измерения

1,5

0,1

0,2

0,3

0

-1,6

-1,3

-1,2

после первого вертикального декодирования

1,1

-1,0

-1,5

1,0

после первого вертикального декодирования

Мягкий выход равен , который после всех четырех итераций дает следующие значения .

2,6

-2,5

-2,6

2,5

В результате видно, что получены правильные решения по каждому биту данных и уровень доверия к этим решениям высок. Итеративное декодирование турбокодов напоминает процесс решения кроссвордов. Первый проход по кроссворду, вероятно, содержит несколько ошибок. Некоторые слова нуждаются в подгонке, но когда буквы в нужных строках и столбцах не подходят, нужно вернуться и исправить слова, вписанные после первого прохода.

8.4.4. Кодирование с помощью рекурсивного систематического кода

Ранее были описаны основные идеи сочетаний, итераций и мягкого декодирования на примере простого композиционного кода. Затем эти идеи применялись при реализации турбокодов, которые образуются в результате параллельных сочетаний сверточных кодов [17, 20].

Далее наступает очередь обзора простых двоичных сверточных кодеров со степенью кодирования 1/2, длиной кодового ограничения K и памятью порядка . На вход кодера в момент k, подается бит , и соответствующим кодовым словом будет битовая пара , где

по мудулю 2, (8.105)

и

по модулю 2, (8.106)

и — генераторы кода, a представлен как двоичная цифра. Этот кодер можно представить как линейную систему с дискретной конечной импульсной характеристикой (finite impulse response — FIR), порождающую хорошо знакомый несистематический сверточный (nonsystematic convolutional — NSC) код, разновидность которого показана на рис. 8.24. Соответствующую решетчатую структуру можно увидеть на рис. 7.7. В данном случае длина кодового ограничения равна К = 3 и используются два генератора кода — и . Хорошо известно, что при больших значениях достоверность передачи с кодом NSC выше, чем у систематического кода с той же памятью. При малых значениях существует обходной путь [17]. В качестве составляющих компонентов для турбокода был предложен класс сверточных кодов с бесконечной импульсной характеристикой [17]. Такие же компоненты используются в рекурсивных систематических сверточных (recursive systematic convolutional — RSC) кодах, поскольку в них предварительно кодированные биты данных постоянно должны подаваться обратно на вход кодера. При высоких степенях кодирования коды RSC дают значительно более высокие результаты, чем самые лучшие коды NSC, при любых значениях . Двоичный код RSC со степенью кодирования 1/2 получается из кода NSC с помощью контура обратной связи и установки одного из двух выходов (или ) равным . На рис. 8.25, а показан пример такого RSC-кода с К = 3, где получается из рекурсивной процедуры

по модулю 2, (8.107)

a равно если , и — если . На рис. 8.25, б изображена решетчатая структура RSC-кода, представленного на рис. 8.25, а.

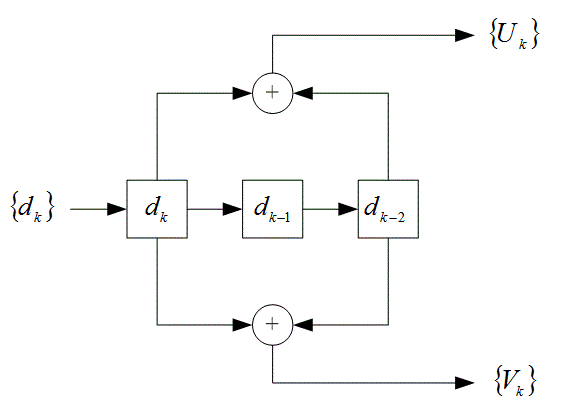
Рис. 8.24. Несистематический сверточный код(nonsystematic convolution - NSC)

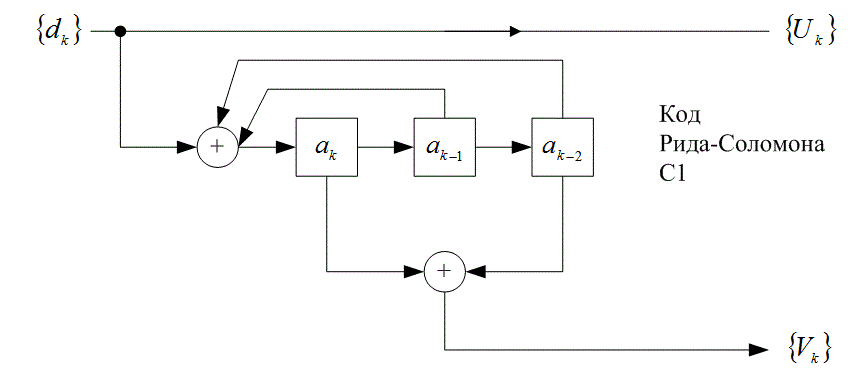
Рис. 8.25а. Рекурсивный систематический

сверточный код (recursive systematic convolution - RSC)

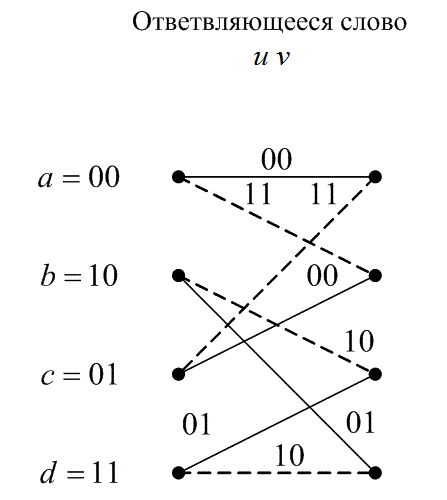
Рис. 8.25б. Решетчатая структура RSC-

кода, представленного на рис. 8.25, а

Считается, что входной бит с одинаковой вероятностью может принимать как значение 1, так и 0. Кроме того, показывает те же статистические вероятности, что [17]: Просвет одинаков у RSC-кода (рис. 8.25, а) и NSC-кода (рис. 8.24). Точно так же совпадает их решетчатая структура по отношению к переходам между состояниями и соответствующим входным битам. Впрочем, у RSC- и NSC-кодов две выходные последовательности и не соответствуют той же входной последовательности . Можно сказать, что при тех же генераторах кода распределение весовых коэффициентов кодовых слов RSC-кодера не изменяется, по сравнению с распределением весовых коэффициентов кодовых слов NSC-кодера. Единственное различие состоит в отображении между входной и выходной последовательностями данных.

Пример 8.5. Рекурсивные кодеры и их решетчатые диаграммы

а) Используя RSC-кодер (рис. 8.25, а), проверьте справедливость участка решетчатой структуры (диаграммы), изображенного на рис. 8.25, б.

б) Для кодера, указанного в п. а, начиная с последовательности данных = 1110, поэтапно покажите процедуру кодирования до нахождения выходного кодового слова.

Решение

а) Для кодеров NSC содержимое регистра и переходы между состояниями отслеживаются непосредственно. Но если кодер является рекурсивным, следует быть очень аккуратным. В табл. 8.5 содержится 8 строк, соответствующих 8 возможным переходам в данной системе, образованной из 4-х состояний. Первые четыре строки представляют переходы, когда входной информационный бит является двоичным нулем, а последние четыре — переходы, в которых является единицей. В данном случае процедуру кодирования с помощью табл. 8.5 и рис. 8.25 можно поэтапно описать следующим образом.

1. В момент введения произвольного входного бита, k, состояние перед переходом (начальное) определяется содержимым двух крайних разрядов регистра, а именно и .

2. В любой строке таблицы (переход на решетке) поиск содержимого разряда выполняется сложением (по модулю 2) битов , и в этой строке.

3. Выходная кодовая последовательность битов, , для каждого возможного начального состояния (т.е. а = 00, b = 10, с = 01 и d = 11) находится путем прибавления (по модулю 2) и к .

Таблица 8.5. Проверка участка решетки с рис. 8.25, б

Входной бит

Текущий бит

Начальное состояние

Кодовые биты

Конечное состояние

0

0

1

1

0

0 0

1 0

0 1

1 1

0 0

0 1

0 0

0 1

0 0

1 1

1 0

0 1

1

1

0

0

1

0 0

1 0

0 1

1 1

1 1

1 0

1 1

1 0

1 0

0 1

0 0

1 1

Нетрудно убедиться, что элементы табл. 8.5 соответствуют участку решетки, изображенному на рис. 8.25, б. При использовании для реализации составных кодов регистров сдвига у турбокодеров проявляется интересное свойство, которое заключается в том, что два перехода, входящие в состояние, не соответствуют одному и тому же входному битовому значению (т.е. в данное состояние не входят две сплошные или две пунктирные линии). Это свойство проявляется, если полиномиальное описание обратной связи регистра сдвига имеет все порядки или одна из линий обратной связи выходит из разряда более высокого порядка, в данном случае .

б) Существует два способа реализации кодирования входной информационной последовательности =1110. Первый состоит в применении решетчатой диаграммы, а другой — в использовании цепи кодера. Воспользовавшись участком решетки, изображенным на рис. 8.25, б, мы выбираем переход по пунктирной линии (представляющий двоичную единицу) из состояния а = 00 (естественный выбор начального состояния) в следующее состояние b = 10 (которое подходит в качестве стартового для следующего входного бита). Следует заметить, что биты показаны на этом переходе как выходная кодовая последовательность 11. Эта процедура повторяется для каждого входного бита. Другой способ предполагает построение таблицы, такой как табл. 8.6, на основе цепи кодера, изображенной на рис. 8.25, а. Здесь время k показано от начала до конца всей процедуры (5 моментов времени и 4 временных интервала). Табл. 8.6 записывается в следующем порядке.

1. В произвольный момент времени бит данных начинает преобразовываться в путем суммирования его (по модулю 2) с битами и в той же строке.

2. Например, в момент времени k = 2 бит данных преобразуется в путем суммирования его с битами и в той же строке k = 2.

3. Итоговый выход , определяемый логической схемой кодера, является кодовой битовой последовательностью, связанной со временем k = 2 (в действительности — интервалом между k = 2 и k = 3).

4. В момент k = 2 содержимое крайних правых разрядов представляет собой состояние системы в начале этого переходам.

5. Конечное состояние этого перехода представляется содержимым двух крайних левых регистров в той же строке (01). Поскольку сдвиг битов происходит слева направо, это конечное состояние перехода в момент k = 3 будет представлено как стартовое в следующей строке.

6. Каждая строка описывается аналогично. Таким образом, в последнем столбце табл. 8.6 можно будет увидеть кодированную последовательность 1 1 1 0 1 1 0 0.

Таблица 8.6. Кодирование битовой последовательности с помощью кодера, изображенного на рис. 8.25, а

Время Входной бит Первый разряд Состояние в момент k Кодовые биты
k
1 1 1 0 0 1 1
2 1 0 1 0 1 0
3 1 0 0 1 1 1
4 0 0 0 0 0 0
5 0 0

8.4.4.1. Конкатенация кодов RSC

Рассмотрим параллельную конкатенацию двух RSC-кодеров, подобных изображенному на рис. 8.25. Хороший турбокод строится из составных кодов с небольшой длиной кодового ограничения (К=3-5). В качестве примера такого турбокодера можно взять кодер, показанный на рис. 8.26, где переключатель делает степень кодирования всего кода равной 1/2. Без переключателя степень кодирования кода будет равна 1/3. Ограничений на количество соединяемых кодеров нет. Составные коды должны иметь одинаковую длину кодового ограничения и степень кодирования. Целью разработки турбохода является наилучший подбор составных кодов путем минимизации просвета кода [21]. При больших значениях это эквивалентно максимизации минимального весового коэффициента кодовых слов. Хотя при низких значениях (область, представляющая наибольший интерес) оптимизация распределения весовых коэффициентов кодовых слов является более важной, чем их максимизация или минимизация [20].

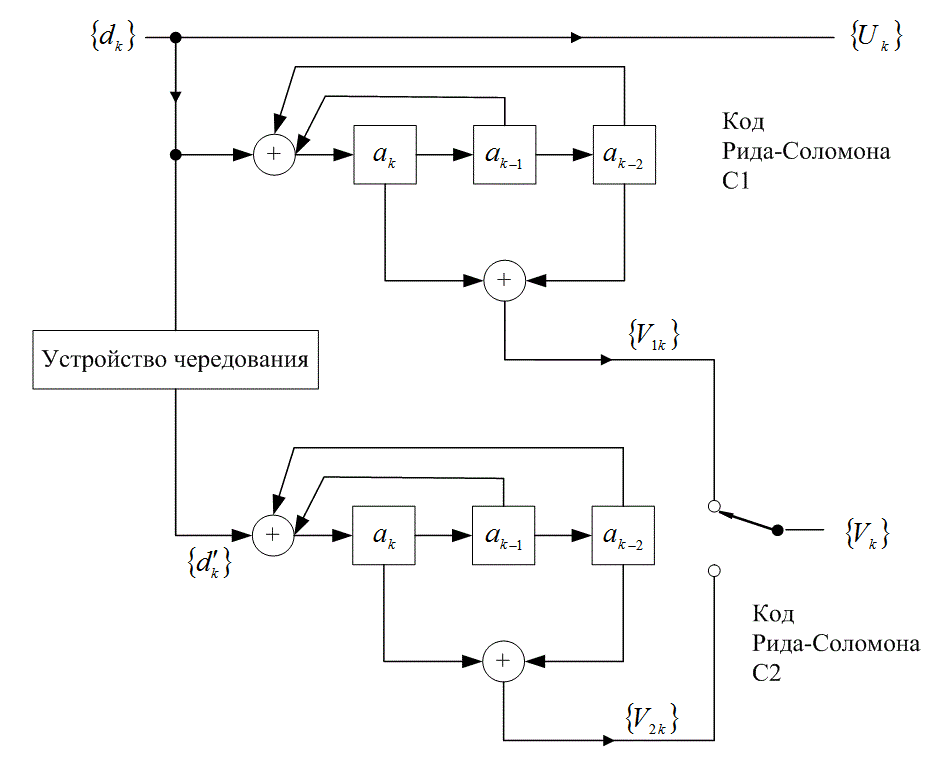
Рис. 8.26. Схема параллельного соединения двух RSC-кодеров

Турбокодер, изображенный на рис. 8.26, выдает кодовые слова из каждого из двух своих составных кодеров. Распределение весовых коэффициентов кодовых слов без такого параллельного соединения зависит от того, сколько кодовых слов из одного составного кодера комбинируется с кодовыми словами из другого составного кодера.

Интуитивно понятно, что следует избегать спаривания кодовых слов с малым весовым коэффициентом из одного кодера с кодовыми словами с малым весовым коэффициентом из другого кодера. Большого количества таких спариваний можно избежать, сконфигурировав надлежащим образом устройство чередования. Устройство, которое обрабатывает данные случайным образом, более эффективно, чем рассмотренное ранее блочное устройство чередования [22].

Если составной кодер не рекурсивный, входная последовательность с единичным весовым коэффициентом (0 0... 0 0 1 0 0 ... 0 0) всегда будет генерировать кодовое слово с малым весовым коэффициентом на входе второго кодера, при любой конструкции устройства чередования. Иначе говоря, устройство чередования не сможет повлиять на выходное распределение весовых коэффициентов кодовых слов, если составные коды не рекурсивные. Впрочем, если составные коды рекурсивные, входная последовательность с единичным весовым коэффициентом генерирует бесконечную импульсную характеристику (выход с бесконечным весовым коэффициентом). Следовательно, при рекурсивных кодах входная последовательность с единичным весовым коэффициентом не дает кодового слова с минимальным весовым коэффициентом вне кодера. Кодированный выходной весовой коэффициент сохраняется конечным только при погашении решетки, процессе, принуждающем кодированную последовательность к переходу в конечное состояние таким образом, что кодер возвращается к нулевому состоянию. Фактически сверточный код преобразуется в блочный.

Для кодера, изображенного на рис. 8.26, кодовое слово с минимальным весовым коэффициентом для каждого составного кодера порождается входной последовательностью с весовым коэффициентом 3 (0 0 ... 0 0 1 1 1 0 0 0 ... 0 0) и тремя последовательными единицами. Другая последовательность, порождающая кодовые слова с малым весом, представлена последовательностью с весом 2 (0 0 ... 0 0 1 0 0 1 0 0 ... 0 0). Однако после перестановок, внесенных устройством чередования, любая из этих опасных структур имеет слабую вероятность появления на входе второго кодера, что делает маловероятной возможность комбинирования одного кодового слова с малым весом с другим кодовым словом с малым весом.

Важным аспектом компоновки турбокодов является их рекурсивность (систематический аспект незначителен). Это бесконечная импульсная характеристика, присущая кодам RSC, которая является защитой от генерации кодовых слов с малым весом, не поддающихся исправлению в устройстве чередования. Можно обсудить то, что производительность турбокодера сильно поддается влиянию со стороны кодовых слов с малым весом, производимых входной последовательностью с весом 2. В защиту этого можно сказать, что входную последовательность с весом 1 можно проигнорировать, поскольку она дает кодовые слова с большим весом из-за бесконечной импульсной характеристики кодера. Для входной последовательности, имеющей вес 3 и более, правильно сконфигурированное устройство чередования делает вероятность появления кодовых слов с малым весом на выходе относительно низкой [21—25].

8.4.5. Декодер с обратной связью

Использование алгоритма Витерби является оптимальным методом декодирования для минимизации вероятности появления ошибочной последовательности. К сожалению, этот алгоритм (с жесткой схемой на выходе) не подходит для генерации апостериорной вероятности (a posteriori probability — АРР) или мягкой схемы на выходе для каждого декодированного бита. Подходящий для этой задачи алгоритм был предложен Балом и др. [26]. Алгоритм Бала был модифицирован Берру и др. [17] для использования в кодах RSC. Апостериорную вероятность того, что декодированный бит данных , можно вывести из совместной вероятности Х., определяемой как

(8.108)

где — состояние кодера в момент времени k, a — принятая двоичная последовательность за время от k = 1 в течение некоторого времени N.

Таком образом, апостериорная вероятность того, что декодированный информационный бит представляется как двоичная цифра, получается путем суммирования совокупных вероятностей по всем состояниям.

(8.109)

Далее логарифмическое отношение правдоподобий (log-likelihood ratio — LLR) переписывается как логарифм отношения апостериорных вероятностей.

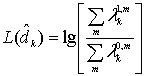(8.110)

Декодер осуществляет схему решений, известную как решающее правило максимума апостериорной вероятности (maximum a posteriori — MAP), путем сравнения с нулевым пороговым значением.

если

(8.111)

если

Для систематического кода LLR , связанное с каждым декодированным битом , можно описать как сумму LLR для dk вне демодулятора и других LLR, порождаемых декодером (внешние сведения), как показано уравнениями (8.72) и (8.73). Рассмотрим обнаружение последовательности данных с помехами, исходящей из кодера, изображенного на рис. 8.26, с помощью декодера, представленного на рис. 8.27. Предполагается, что используется двоичная модуляция и дискретный гауссов канал без памяти. Вход декодера формируется набором Rk из двух случайных переменных и . Для битов и , которые в момент времени k представляются двоичными числами (1, 0), переход к принятым биполярным импульсам (+1, -1) можно записать следующим образом.

(8.112)

и

(8.113)

Здесь и являются двумя случайными статистически независимыми переменными с одинаковой дисперсией , определяющей распределение помех. Избыточная информация yk разуплотняется и пересылается на декодер DEC1 как , если , и на декодер DEC2 как , если . Если избыточная информация начальным декодером не передается, то вход соответствующего декодера устанавливается на нуль. Следует отметить, что выход декодера DEC1 имеет структуру чередования, аналогичную структуре, использованной в передатчике между двумя составными кодерами. Это связано с тем, что информация, обрабатываемая декодером, DEC1, является неизмененным выходом кодера С1 (искаженной канальным шумом). И наоборот, информация, обрабатываемая декодером DEC2, является искаженным выходом кодер С2, вход которого составляют как раз те данные, что поступают в С1, но обработаны устройством чередования. Декодер DEC2 пользуется выходом декодера DEC1, обеспечивая такое же временное упорядочение этого выхода, как и входа С2 (т.е. две последовательности в декодере DEC2 должны придерживаться позиционной структуры сигналов в каждой последовательности).

8.4.5.1. Декодирование при наличии контура обратной связи

Уравнение (8.71) можно переписать для мягкого выхода в момент времени k с нулевой начальной установкой априорного LLR . Это делается на основе предположения о равной вероятности информационных битов. Следовательно,

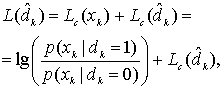(8.114)

где — мягкий выход декодера, а — LLR канального измерения, получаемый из отношения функций правдоподобия , связанных с моделью дискретного канала без памяти является функцией избыточной информации. Это внешние сведения, получаемые декодером и не зависящие от входных данных xk декодера. В идеале Lc(xk) и искажаются некоррелированным шумом, а следовательно, может использоваться как новое наблюдение другим декодером для образования итеративного процесса. Основным принципом передачи информации обратно на другой декодер является то, что декодер никогда не следует заполнять собственными данными (иначе искажения на входе и выходе будут сильно коррелировать).

Для гауссового канала в уравнении (8.114) при описании канального LLR Lc(xk) использовался натуральный логарифм, как и в уравнении (8.77). Уравнение (8.77,в) можно переписать следующим образом.

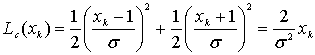(8.115)

Оба декодера, DEC1 и DEC2, используют модифицированный алгоритм Бала [26]. Если данные и подаваемые на вход декодера DEC2 (рис. 8.27), являются статистически независимыми, то LLR на выходе декодера DEC2 можно переписать как

(8.116)

при

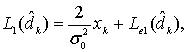(8.117)

где используется для выражения функциональной зависимости. Внешние сведения вне декодера DEC2 являются функцией последовательности Поскольку зависит от наблюдения , внешние сведения коррелируют с наблюдениями xk и Тем не менее, чем больше значение тем меньше коррелируют и наблюдения и . Вследствие чередования выходов декодеров DEC1 и DEC2, внешние сведения слабо коррелируют с наблюдениями и . Поэтому можно совместно использовать их для декодирбвания битов [17]. На рис. 8.27 показана процедура подачи параметра на декодер DEC1 как эффект разнесения в итеративном процессе. Вообще, имеет тот же знак, что и . Следовательно, может увеличить соответствующее LLR и, значит, повысить надежность каждого декодированного бита данных.

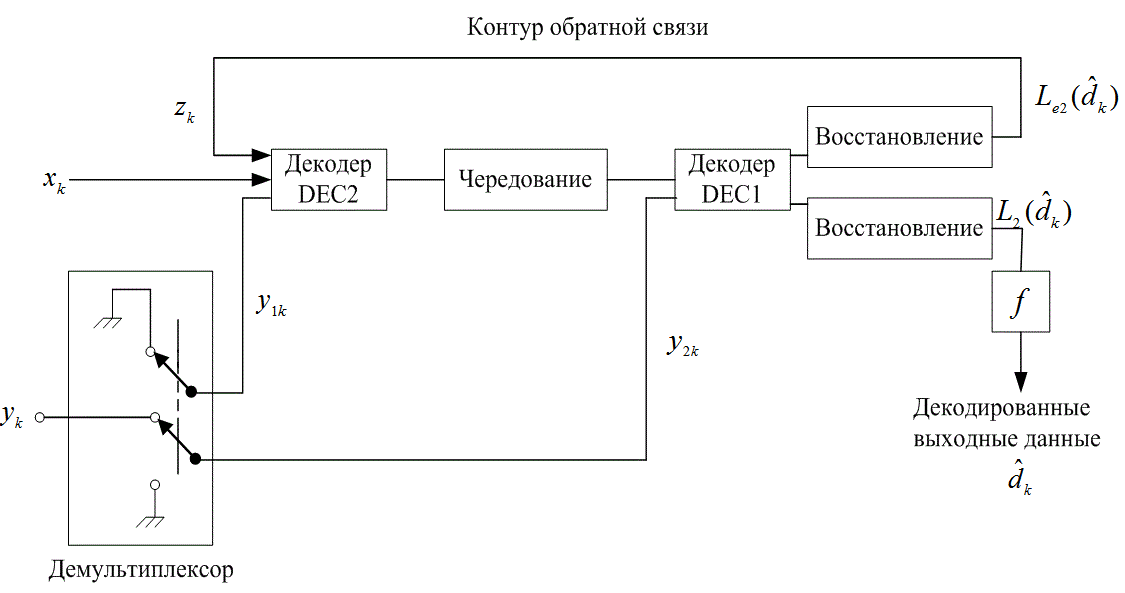
Рис. 8.27 Схема оекооера с ооратнои связью

Подробное описание алгоритма вычисления LLR апостериорной вероятности каждого бита данных было представлено несколькими авторами [17, 18, 30]. В работах [27—31] были высказаны предположения относительно снижения конструктивной сложности алгоритмов. Приемлемый подход к представлению процесса, дающего значения апостериорной вероятности для каждого информационного бита, состоит в реализации оценки максимально правдоподобной последовательности, или алгоритма Витерби, и вычислении ее по двум направлениям блоков кодовых битов. Если осуществлять такой двунаправленный алгоритм Витерби по схеме раздвижных окон — получатся метрики, связанные с предшествующими и последующими состояниями. В результате получим апостериорную вероятность для каждого бита данных, имеющегося в блоке. Итак, декодирование турбоходов можно оценить как в два раза более сложное, чем декодирование одного из составных кодов с помощью алгоритма Витерби.

8.4.5.2. Достоверность передачи при турбокодировании

В [17] приведены результаты моделирования методом Монте-Карло кодера со степенью кодирования 1/2, K = 5, построенного на генераторах = {1 1 1 1 1} и = {1 0 0 0 1}, при параллельном соединении и использовании устройства чередования с массивом . Был использован модифицированный алгоритм Бала и блок, длиной 65536 бит. После 18 итераций декодирования вероятность появления ошибки в бите была меньше при дБ. Характер снижения вероятности появления ошибки при увеличении числа итераций можно увидеть на рис. 8.28. Заметьте, что достигается предел Шеннона -1,6 дБ. Требуемая ширина полосы пропускания приближается к бесконечности, а емкость (степень кодирования кода) приближается к нулю. Поэтому предел Шеннона является интересной границей с теоретической точки зрения, но не является практической целью. Для двоичной модуляции несколько авторов использовали в качестве практического предела Шеннона значения и дБ для кода со степенью кодирования 1/2. Таким образом, при параллельном соединении сверточных кодов RSC и декодировании с обратной связью, достоверность передачи турбокода при находится в 0,5 дБ от (практического) предела Шеннона. Существует класс кодов, в которых, вместо параллельного, используется последовательное соединение чередуемых компонентов. Предполагается, что последовательное соединение кодов может дать характеристики [28], превышающие аналоги при параллельном соединении.

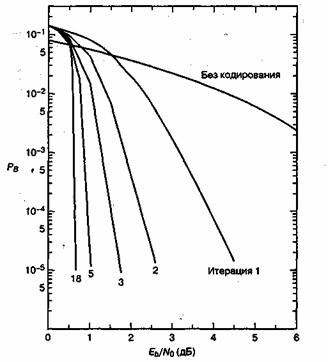
Рис. 8.28. Вероятность появления битовой ошибки как функция Eb/N0 и количества итераций. (Источник: Berrou С., Glavieux A. and Thitimajshima P. "Near Shannon Limit Error-Correcting Coding and Decoding: Turbo Codes". IEEE Proc. of Int'l Conf on Communications, Geneva, Switzerland, May, 1993 (ICC '93), pp. 1064-1070.)

8.4.6. Алгоритм MAP

Процесс декодирования турбокода начинается с формирования апостериорных вероятностей (a posteriori probability — АРР) для всех информационных битов, которые затем используются для изменения значений информационных битов в соответствии с принципом максимума апостериорной (maximum a posteriori— MAP) вероятности информационного бита. В ходе приема искаженной последовательности кодированных битов осуществляется схема принятия решений, основанная на значениях апостериорных вероятностей, и алгоритм MAP для определения наиболее вероятного информационного бита, который должен быть передан за время прохождения бита. Здесь имеется отличие от алгоритма Витерби, в котором апостериорная вероятность для каждого бита данных не существует. Вместо этого в алгоритме Витерби находится наиболее вероятная последовательность, которая могла быть передана. Но в реализации обоих алгоритмов, впрочем, имеется сходство (см. раздел 8.4.6.3). Если декодированное мало, существует незначительное различие в производительности между алгоритмами MAP и Витерби с мягкий выходом (soft-output Viterbi algorithm— SOVA). Более того, при высоких значениях и низких значениях алгоритм MAP превосходит алгоритм SOVA на 0,5 дБ и более [30, 31]. Это может оказаться очень важным для турбокодов, поскольку первая итерация декодирования может давать довольно высокую вероятность ошибки. Алгоритм MAP основывается на той же идее, что и алгоритм Витерби, — обработка блоков кодовых битов в двух направлениях. Как только такое двунаправленное вычисление даст состояние и метрики ветвей блока, можно начинать расчет апостериорной вероятности и MAP для каждого бита данных в блоке. Здесь предлагается алгоритм MAP декодирования для систематических сверточных кодов; полагается, что используется канал AWGN, как указано Питробоном [30]. Расчет начинается с отношения значений апостериорных вероятностей, известных как отношения правдоподобий , или их логарифмов, , называемых логарифмическими отношениями правдоподобий (log-likelihood ratio — LLR), как было показано в уравнении (8.110).

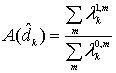(8.118,a)

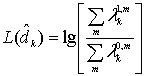(8.119,б)

Здесь (совокупная вероятность того, что и , при условии, что принята кодовая последовательность , получаемая с момента k = 1 в течение некоторого времени N) определяется уравнением (8.108) и повторно риводится ниже.

(8.119)

где представляет искаженную последовательность кодированных битов, передаваемую по каналу, демодулированную и поданную на декодер согласно мягкой схеме решений. В действительности, алгоритм MAP требует, чтобы последовательность на выходе демодулятора подавалась на декодер по одному блоку из N бит за такт. Пусть имеет следующий вид.

(8.120)

Чтобы упростить применение теоремы Байеса, уравнение (8.119) переписывается с использованием букв А, В, С и D. Таким образом, уравнение (8.119) примет следующий вид.

(8.121)

Вспомним, что теорема Байеса гласит следующее.

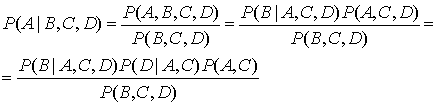(8.122)

Отсюда, в приложении теоремы к уравнению (8.121) получается следующее.

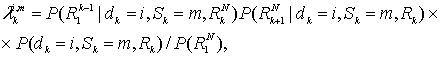(8.123)

причем . Уравнение (8.123) можно переписать, выделяя вероятностный член, вносящий вклад . В следующем разделе три множителя в правой части уравнения (8.123) будут определены и описаны как прямая метрика состояния, обратная метрика состояния и метрика ветви.

8.4.6.1. Метрики состояний и метрика ветви

Первый множитель в правой части уравнения (8.123) является прямой метрикой состояния для момента k и состояния т и обозначается . Таким образом, для i = 1,0

(8.124)

Следует отметить, что dk = i и обозначены как несущественные, поскольку предположение о том, что , подразумевает, что на события до момента k не влияют измерения после момента k. Другими словами, будущее не оказывает влияния на прошлое; таким образом, не зависит от того, что dk = i и последовательность равна . В то же время, поскольку кодер обладает памятью, состояние кодера основывается на прошлом, а значит, этот член является значимым и его следует оставить в выражении. Очевидно, что форма уравнения (8.124) является понятной, поскольку представляет прямую метрику состояния для момента k как вероятность того, что прошлая последовательность зависит только от теперешнего состояния, вызванного этой последовательностью и ничем более. В этом сверточком кодере нетрудно узнать уже упоминавшийся в главе 7 Марковский процесс.

Точно так же второй сомножитель в правой части уравнения (8.123) представляет собой обратную метрику состояния для момента времени k и состояния т, определяемую следующим выражением.

(8.125)

Здесь — это следующее состояние, определяемое входом i и состоянием т, - обратная метрика состояния в момент и состояние .Ясно, что уравнение (8.125) удовлетворяется, поскольку обратная метрика состояния (в будущий момент времени представлена как вероятность будущей последовательности, которая зависит от состояния (в будущий момент ), которое, в свою очередь, является функцией входного бита и состояния (в текущий момент k).Это уже знакомое основное определение конечного автомата (см. раздел 7.2.2).

Третий сомножитель в правой части уравнения (8.123) представляет собой метрику ветви (в состоянии т, в момент времени k), которая обозначается . Таким образом, можно записать следующее.

(8.126)

Подстановка уравнений (8.124)-(8.126) в уравнение (8.123) дает следующее, более компактное выражение для совокупной вероятности.

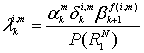(8.127)

Используя уравнение (8.127), формулу (8.118) можно представить следующим образом.

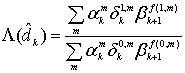(8.128,a)

и

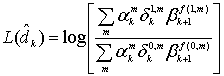(8.128,6)

Здесь — это отношение правдоподобий k-го бита данных; , логарифм , является логарифмическим отношением правдоподобий для k-го бита данных, где, в общем случае, логарифм берется по основанию е.

8.4.6.2. Расчет прямой метрики состояния

Исходя из уравнения (8.124), можно представить как сумму всех возможных переходов из момента .

(8.129)

можно переписать как и, согласно теореме Байеса,

(8.130,а)

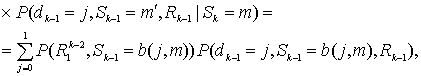(8.130,б)

где — это состояние по предыдущей ветви, соответствующей входу j, исходящее обратно по времени из состояния т. Уравнение (8.130,6) может заменить уравнение (8.130,а), поскольку сведения о состоянии и входе j в момент времени полностью определяют путь в состояние . Воспользовавшись уравнениями (8.124) и (8.126) для упрощения обозначений в уравнении (8.130), можно получить следующее.

(8.131)

Уравнение (8.131) означает, что новая прямая метрика состояния т в момент k получается из суммирования двух взвешенных метрик состояний в момент . Взвешивание включает метрики ветвей, связанные с переходами, соответствующими информационным битам 1 и 0. На рис. 8.29, а показано применение двух разных типов обозначений для параметра . Запись используется для обозначения прямой метрики состояния в момент времени , если имеется два возможных предыдущих состояния (зависящих от того, равно ли j единице или нулю). А запись применяется для обозначения прямой метрики состояния в момент k, если имеется два возможных перехода из предыдущего момента, которые оканчиваются в том же состоянии т в момент k.

Рис. 8.29. Графическое представление расчета и . (Источник: Pietrobon S. S. "Implementation and Performance of a Turbo/Map Decoder". Int'l. J. of Satellite Communications, vol. 16, Jan.-Feb., 1998, pp. 23-46.)

8.4.6.3. Расчет обратной метрики состояния

Возвращаясь к уравнению (8.125), где , имеем следующее.

(8.132)

можно представить как сумму вероятностей всех возможных переходов в момент .

(8.133)

Применяя теорему Байеса, получим следующее.

(8.134)

В первом члене правой части уравнения (8.134) и полностью определяют путь, ведущий в следующее состояние будет иметь вход j и состояние т. Таким образом, эти условия позволяют заменить на во втором члене уравнения (8.134), что дает следующее.

(8.135)

Уравнение (8.135) показывает, что новая обратная метрика состояния т в момент k, получается путем суммирования двух взвешенных метрик состояния в момент . Взвешивание включает метрики ветвей, связанные с переходами, соответствующими информационным битам 1 и 0. На рис. 8.29, б показано применение двух разных типов обозначений для параметра . Первый тип, запись , используется для обозначения обратной метрики состояния в момент времени , если имеется два возможных предыдущих состояния (зависящих от того, равно ли j единице или нулю). Второй тип, , применяется для обозначения обратной метрики состояния в момент k, если имеется два возможных перехода, поступающих в момент , которые выходят из того же состояния т в момент времени k На рис. 8.29 приведены пояснения к вычислениям прямой и обратной метрик.

Алгоритм декодирования MAP подобен алгоритму декодирования Витерби (см. разделЛ.З). В алгоритме Витерби метрика ветви прибавляется к метрике состояния. Затем сравнивается и выбирается минимальное расстояние (максимально правдоподобное) для получения следующей метрики состояния. Этот процесс называется сложение, сравнение и выбор (Add-Compare-Select — ACS). В алгоритме MAP выполняется умножение (в логарифмическом представлении — сложение) метрик состояния и метрик ветвей. Затем, вместо сравнения, осуществляется их суммирование для вычисления следующей прямой (обратной) метрики состояния, как это видно из рис; 8.29. Различия, воспринимаются на уровне интуиции. В алгоритме Витерби осуществляется поиск наиболее вероятной последовательности (пути); следовательно, выполняется постоянное сравнение и отбор, для того чтобы отыскать наилучший путь. В алгоритме MAP выполняется поиск правдоподобного или логарифмически правдоподобного числа (в мягкой схеме); следовательно, за период времени процесс использует все метрики из всех возможных переходов, чтобы получить полную статистическую картину информационных битов в данном периоде времени.

8.4.6.4. Расчет метрики ветви

Сначала обратимся к уравнению (8.126).

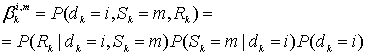(8.136)

Здесь Rk представляет собой последовательность , — это принятые биты данных с шумом, a — принятые контрольные биты с шумом. Поскольку помехи влияют на информационные биты и биты контроля четности независимо, текущее состояние не зависит от текущего входа и, следовательно, может быть одним из состояний, где — это число элементов памяти в сверточной кодовой системе. Иными словами, длина кодового ограничения этого кода, К, равняется . Значит,

и

, (8.137)

где обозначает , априорную вероятность dk.

Из уравнения (1.25,г) в главе 1, вероятность того, что случайная переменная Xk примет значение xk, связана с функцией плотности вероятности следующим образом.

(8.138)

Для упрощения обозначений случайная переменная , принимающая значение , часто будет называться “случайной переменной ”, которая будет представлять значения и в уравнении (8.137). Таким образом, для канала AWGN, в котором шум имеет нулевое среднее и дисперсию , при замене вероятностного члена в уравнении (8.137) его эквивалентом (функцией плотности вероятности) используется уравнение (8.138), что дает следующее.

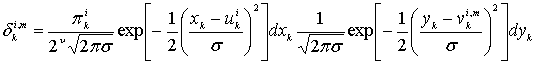(8.139)

Здесь и представляют переданные биты данных и биты контроля четности (в биполярной форме), a и являются дифференциалами xk и yk и далее будут включаться в постоянную Ak. Следует заметить, что параметр представляет данные, не зависящие от состояния т, поскольку код имеет память. Для того чтобы привести выражение к более простому виду, нужно исключить все члены в числителе и знаменателе и использовать сокращения; в результате получим следующее.

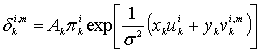(8.140)

Если подставить уравнение (8.140) в уравнение (8.128,а), получим следующее.

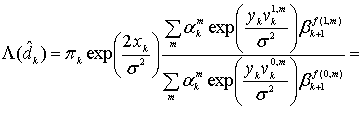(8.141,a)

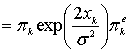(8.141,б)

и

(8.141,в)

Здесь является входным отношением априорных вероятностей (априорное правдоподобие), a — внешним выходным правдоподобием, каждое в момент времени k. В уравнении (8.141,б) член можно считать фактором коррекции (вследствие кодирования), который меняет входные априорные сведения о битах данных. В турбокоде такие корректировочные члены проходят из одного декодера в другой, чтобы улучшить отношение правдоподобий для каждого информационного бита и, таким образом, минимизировать вероятность появления ошибок декодирования. Следойательно, процесс декодирования влечет за собой использование уравнения (8.141,б) для получения за несколько итераций . Внешнее правдоподобие , получаемое из конкретной итерации, заменяет априорное правдоподобие на следующую итерацию. Взятие логарифма от в уравнении (8.141,б) дает уравнение (8.141,в), которое показывает те же результаты, что и уравнение (8.71). Они заключаются в том, что итоговые данные (согласно мягкой схеме принятия решений) образуются тремя членами LLR — априорным LLR, LLR канального измерения и внешним LLR.

Алгоритм MAP можно реализовать через отношение правдоподобий , как показывает уравнение (8.128,а) или (8.141,в); конструкция станет менее громоздкой за счет устранения операций умножения.

8.4.7. Пример декодирования по алгоритму MAP

На рис. 8.30 изображен пример декодирования по алгоритму MAP. На рис. 8.30, а представлен систематический сверточный кодер с длиной кодового ограничения и степенью кодирования 1/2. Входные данные - последовательность d = {1, 0, 0}, соответствующая временам k = 1,2,3. Выходная кодированная битовая последовательность образуется путем последовательного взятия одного бита из последовательности v = {1, 0, 0} вслед за битом контроля четности из последовательности v={ 1, 0, 1}. В каждом случае крайний слева бит является самым первым. Таким образом, выходной последовательностью будет 1 1 0 0 0 1 или ее биполярное представление — +1 +1 -1 -1 -1 +1. На рис. 8.30, б видны результаты искажения последовательностей u и v векторами помех и , так что теперь они обозначаются как , и . Как показано на рис. 8.30, б, входные данные демодулятора, поступающие на декодер в моменты k = 1, 2, 3, имеют значения 1,5; 0,8; 0,5; 0,2; -0,6; 1,2. Также показаны априорные вероятности того, что принятые биты данных будут равны 1 или 0, что обозначается как и . Предполагается, что эти вероятности будут одинаковы для всех k моментов времени. В этом примере уже имеется вся необходимая информация для расчета метрик ветвей и метрик состояний и ввода их значений в решетчатую диаграмму декодера, изображенную на рис. 8.30, в. На решетчатой диаграмме каждый переход, возникающий между временами k и , соответствует информационному биту dk, который появляется на входе кодера в момент начала перехода k. В момент времени k кодер находится в некотором состоянии т, а в момент он переходит в новое состояние (возможно, такое же). Если использовать такую решетчатую диаграмму для отображения последовательности кодовых битов (представляющих N бит данных), последовательность будет описываться N временами переходов и состояниями.

8.4.7.1. Расчет метрик ветвей

Начнем с уравнения (8.140) при (в данном примере информационные биты считаются равновероятными для любых времен). Для простоты предполагается, что для всех моментов и . Таким образом, примет следующий вид.

(8.142)

На что похожа основная функция приемника, определяемая уравнением (8.142)? Выражение напоминает корреляционный процесс. В декодере в каждый момент k принимается пара данных,( относящееся к битам данных, и , относящееся к контрольным битам). Метрика ветви рассчитывается путем умножения принятого на каждый первообразный сигнал uk и принятого yk на каждый первообразный сигнал . Для каждого перехода по решетке величина метрики ветви будет функцией того, насколько согласуются пара данных, принятых с помехами, и кодовые значения битов этого перехода по решетке. При для вычисления восьми метрик ветвей (переходов из состояний т для всех значений данных i) применяется уравнение (8.142). Для простоты, состояния на решетке обозначены следующим образом: а = 00, b = 10, с = 01, d = 11. Заметьте, что кодированные битовые значения, , , каждого перехода по решетке указаны над самими переходами, как можно видеть на рис. 8.30, в (только для ), и их можно получить обычным образом, используя структуру кодера (см. раздел 7.2.4.). Для переходов по решетке на рис. 8.30, в оговаривается, что пунктирные и сплошные линии обозначают информационные биты 1 и 0. Расчеты дают такие значения.

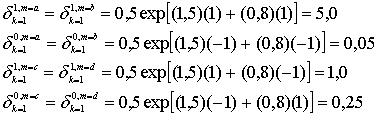
Затем эти расчеты повторяются, с помощью уравнения (8.142), для восьми метрик ветвей в момент k = 2.

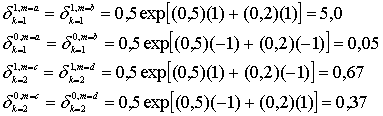
Снова расчеты повторяются для значений восьми метрик ветвей уже в момент k =3.

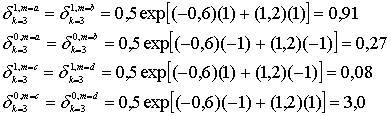
8.4.7.2. Расчет метрик состояний

Как только при всех k рассчитаны восемь значений , можно вычислить прямые метрики состояний , воспользовавшись рис. 8.29, 8.30, в и уравнением (8.131), которое повторно приводится ниже.

Допустим, что начальным состоянием кодера будет а = 00. Тогда,

и

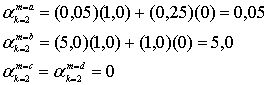и т.д.

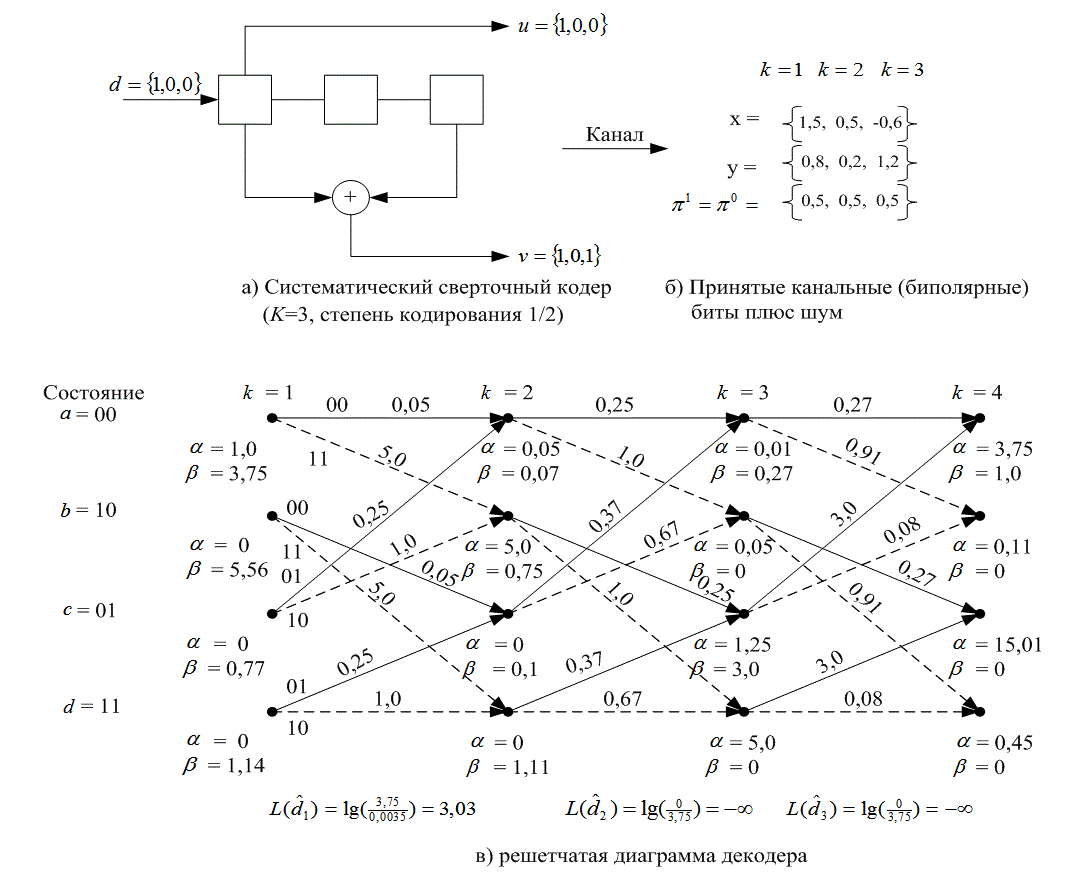
Рис. 8.30. Пример декодирования по алгоритму MAP (К = 3, степень кодирования 1/2, систематическое)

как показано с помощью решетчатой диаграммы на рис. 8.30, в. Аналогично можно вычислить обратные метрики состояний , воспользовавшись рис. 8.29, 8.30, в и уравнением (8.135), которое повторно приводится ниже.

Последовательность данных и код в этом примере умышленно были изменены так, что финальным состоянием решетки в момент времени k = 4 является а = 00. В противном случае нужно использовать остаточные биты для принудительного изменения конечного состояния системы в такое известное состояние. Таким образом, в этом примере, проиллюстрированном на рис. 8.30, исходя из того, что конечное состояние — а = 00, можно рассчитать обратные метрики состояний.

и

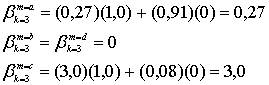
Все значения обратных метрик состояний показаны на решетке (рис. 8.30, в).

8.4.7.3. Расчет логарифмического отношения правдоподобий

Теперь у нас есть рассчитанные метрики , , и для кодированной битовой последовательности рассматриваемого примера. В процессе турбодекодирования для нахождения решения согласно мягкой схеме, или , для каждого бита данных можно воспользоваться уравнением (8.128) или (8.141). При использовании турбокодов этот процесс повторяется несколько раз, чтобы достичь необходимой надежности решений. В целом все заканчивается применением параметра внешнего правдоподобия из уравнения (8.141,б) для вычисления и повторного расчета в несколько итераций отношения правдоподобий . Внешнее правдоподобие последней итерации заменяет в следующей итерации априорное правдоподобие .

В нашем примере будут использованы метрики, рассчитанные ранее (с одним прохождением через декодер). Для вычисления LLR каждого информационного бита в последовательности берется уравнение (8.128,б). Затем, с помощью правила принятия решений из уравнения (8.111), итоговые данные, представленные согласно мягкой схеме решений, преобразуются в решения в жесткой схеме. Для , опуская некоторые нулевые слагаемые, получаем следующее.

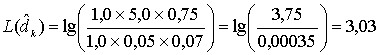
Для k = 2, опуская некоторые нулевые слагаемые, получаем следующее.

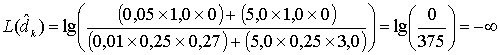
Для k = 3

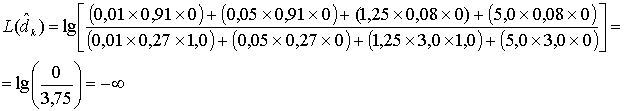
С помощью уравнения (8.111) для выражения финального решения относительно битов в моменты k = 1,2,3, последовательность декодируется как {1 0 0}. Итак, получен абсолютно точный результат, совпадающий с теми данными, которые были введены в декодер.

8.4.7.4. Реализация конечного автомата с помощью регистра сдвига

В этой книге используются регистры сдвига с прямой и обратной связью, представленные по большей части как разряды памяти и соединительные линии. Важно обратить внимание на то, что часто оказывается удобным представлять кодер (конкретнее, рекурсивный кодер) на регистрах сдвига несколько иным образом. Некоторые авторы для обозначения временных задержек (как правило, длиной в 1 бит) используют блоки, помеченные буквами D или Т. Соединения вне блоков, передающие напряжение или логические уровни, представляют память кодера между тактами. Два формата — блоки памяти и блоки задержек — никоим образом не меняют характеристик или функционирования описанного выше процесса. Для некоторых конечных автоматов с множеством рекурсивных соединений при отслеживании сигналов более удобным может оказаться применение формата блоков задержек. В задачах 8.23 и 8.24 используются кодеры, изображенные на рис. 38.2 и 38.3. При использовании формата разрядов памяти текущее состояние системы определяется содержимым крайних правых разрядов. Аналогично для формата блоков задержек текущее состояние определяется уровнями сигналов в крайних правых узлах (соединения вне блоков задержек). Для обоих форматов связь между памятью v и длиной кодового ограничения K одинакова, т.е. . Таким образом, на рис. 38.2 три блока задержек означают, что v = 3 и . Аналогично на рис. 38.3 два блока задержек означают, что , а .