В любой реализуемой системе, выполняющей неидеальную фильтрацию, будет межсимвольная интерференция (intersymbol interference, ISI) — хвост одного импульса распространяется на соседние символы и мешает процессу обнаружения. Найквист [2] показал, что теоретическая минимальная ширина полосы пропускания (ширина полосы частот по Найквисту), требуемая для немодулированной передачи R, символов за секунду без межсимвольной интерференции, составляет R/2 Гц. Это основное теоретическое ограничение, вынуждающее разработчика настолько аккуратно использовать полосу частот, насколько это возможно (см. раздел 3.3). На практике минимальная ширина полосы частот по Найквисту увеличивается на 10-40% вследствие ограничений реальных фильтров. Таким образом, реальная пропускная способность цифровых систем связи снижается с идеальных, 2 символа/с/Гц до 1,8-1,4 символа/с/Гц. Из набора М символов, система модуляции или кодирования присваивает каждому символу it-битовое значение, где . Таким образом, число битов на символ можно представить как , и, следовательно, скорость передачи данных, или скорость передачи битов R, должна быть в k раз больше скорости передачи символов , как видно из следующего основного соотношения.

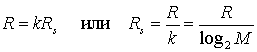(9.1)

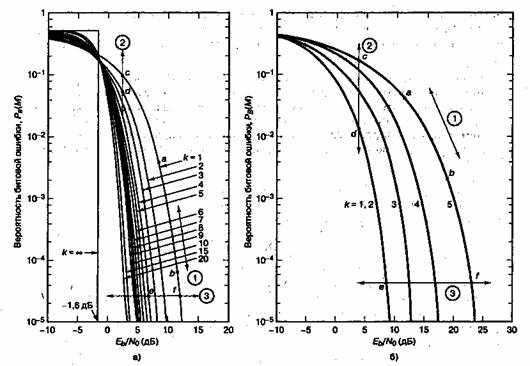
Рис. 9.1. Зависимость вероятности появления битовой ошибки от при когерентном обнаружении М-арных сигналов: а) ортогональные сигналу; б) многофазные сигналы

Для системы с фиксированной скоростью передачи символов из выражения (9.1) видно, что с ростом k увеличивается и скорость передачи битов R. При использовании схемы MPSK с увеличением k повышается эффективность использования полосы частот R/W, измеряемая в бит/с/Гц. Например, сдвиг вдоль линии 3, из точки е в точку f, как видно на рис. 9.1, б представляет собой повышение за счет снижения требований к полосе пропускания. Другими словами, при той же полосе пропускания сигналы, модулированные MPSK, можно передавать с повышенной скоростью передачи данных, а значит с увеличенным R/W.

Пример 9.1. Классификация схем цифровой модуляции

В некотором смысле все схемы цифровой модуляции относятся к одному из двух классов с противоположными характеристиками. Первый класс — это передача ортогональных сигналов; достоверность такой передачи описывается кривыми на рис. 9.1, а. Ко второму классу относится передача неортогональных сигналов (набор векторов сигналов можно отобразить на плоскости). На рис. 9.1, б представлен пример передачи неортогональных сигналов — модуляция MFSK. Вообще, любая фазовая/амплитудная модуляция (например, QAM) относится ко второму классу. Используя рис. 9.1, ответьте на следующие вопросы.

а) Как в случае М-арной передачи сигналов будет меняться достоверность передачи (увеличиваться или снижаться) при повышении M?

б) Возможности выбора в цифровой связи почти всегда сопряжены с компромиссами. Если достоверность передачи растет, то за счет чего?

в) Если растет вероятность появления ошибки, то какую выгоду можно получить из этого?

Решение

а) Из рис. 9.1 можно видеть, что повышение или снижение достоверности передачи зависит от рассматриваемого класса передачи сигналов. Рассмотрим передачу ортогональных сигналов (рис. 9.1, а), где достоверность передачи растет с увеличением k или М. Напомним, что существует лишь два способа сравнения подобных характеристик Достоверности передачи. Можно провести вертикальную линию при некотором фиксированном значении и увидеть, что при уменьшении k или М снижается. Или наоборот, можно провести горизонтальную линию, фиксирующую некоторое значение РВ, и с ростом k или М отметить снижение требований к . Точно так же на рис. 9.1, б можно видеть, что при неортогональной передаче, такой как модуляция MPSK, характеристики ведут себя абсолютно иначе. Достоверность передачи снижается при увеличении k или М.

б) Чем мы платим за передачу ортогональных (сигналов, при которой достоверность передачи повышается с ростом k или М? Наиболее распространенным вариантом передачи ортогональных сигналов является схема MFSK, где k = 1и М = 2, а набор тонов состоит из двух сигналов. Если k = 2 и М = 4, в наборе уже содержится четыре тона. При k = 3 и М = 8 будет уже восемь сигналов и т.д. При использовании схемы MFSK за время передачи символа отсылается только один тон, но доступная полоса пропускания — это весь набор тонов. Следовательно, при увеличении k или М за повышение достоверности передачи придется платить расширением требуемой полосы пропускания.

в) При передаче неортогональных сигналов (схема MPSK или QAM) с ростом k или М достоверность передачи падает. Логично предположить, что компромисс повлечет за собой снижение требований к полосе пропускания. Рассмотрим следующий пример. Пусть требуется Скорость передачи данных R = 9600 бит/с, а в качестве модуляции используется 8-уровневая схема PSK. Тогда с помощью уравнения (9.1) скорость передачи символов находится следующим образом.

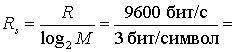3200 символов/с

Если для передачи воспользоваться 16-уровневой схемой PSK, то скорость передачи символов будет равна следующему.

2400 символов/с

Если применить 32-уровневую схему PSK, скорость передачи символов будет равна

1920 символов/с.

Что происходит, когда на рис. 9.1, б рабочая точка сдвигается вдоль горизонтальной линии с кривой с k = 3 на кривую с k = 4 и далее на кривую с k = 5? При данной скорости передачи данных и вероятности появления ошибки каждый такой сдвиг позволяет осуществлять передачу на все более низких скоростях. Всякий раз, когда говорится "более низкая скорость передачи сигнала", это эквивалентно сообщению, что имеется возможность уменьшить ширину полосы пропускания. Аналогично любое повышение скорости передачи сигналов соответствует увеличению ширины полосы пропускания.