4.8.1. Идеальная достоверность передачи
4.8.2. М-арная передача сигналов
4.8.3. Векторное представление сигналов MPSK
4.8.4. Схемы BPSK и QPSK имеют одинаковые вероятности ошибки
4.8.1. Идеальная достоверность передачи
На рис. 3.6 приводился характерный, "водопадоподобный" график зависимости вероятности ошибки от отношения 
. Как видно из рис.4.25, вероятность появления ошибочного бита (РB) для различных бинарных схем модуляции при наличии AWGN также имеет подобную форму. А на что будет похож график зависимости идеальной РB от ? Ответ, в виде предела Шеннона, приведен на ри.с. 4.27. Этот предел представляет порог , ниже которого поддержание достоверной связи невозможно. Подробно работа Шеннона рассмотрена в главе 9.
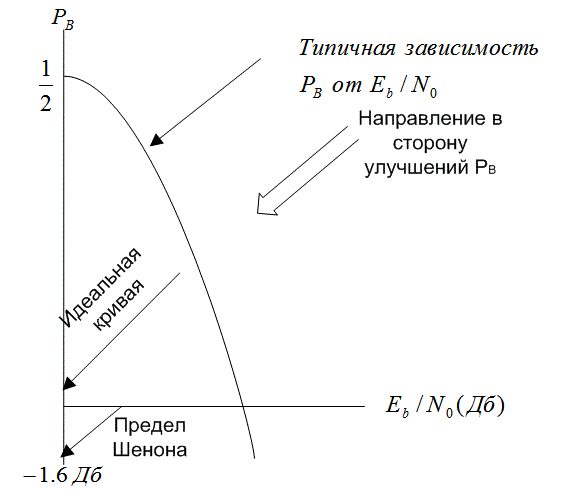
Рис. 4.27. Зависимость идеальной 
Идеальную кривую на рис. 4.27 можно описать следующим образом. Для всех значений 
, находящихся выше предела Шеннона (-1,6 дБ), РB равно нулю. Как только падает ниже предела Шеннона, РB в худшем случае возрастает до 1/2. (Отметим, что РB = 1 — это не самый неблагоприятный вариант для бинарной передачи сигналов, поскольку это значение аналогично РB = 0; если вероятность появления ошибочного бита равна 100%, то для восстановления точной информации поток битов просто можно инвертировать.) На рис. 4.27 большой стрелкой показано направление повышения достоверности передачи от типичной к идеальной вероятности РB.
4.8.2. М-арная передача сигналов
Рассмотрим M-арную передачу сигналов. В каждый момент времени процессор рассматривает k бит. Он указывает модулятору произвести один из М=2k сигналов; частным случаем k= 1 является бинарная передача сигналов. Как увеличение k влияет на достоверность передачи — снижает или повышает ее? (Не спешите отвечать — вопрос с подвохом.) На рис. 4.28 показана зависимость вероятности появления ошибочного бита 
для ортогональной M-уровневой передачи сигналов по каналу с гауссовым шумом при использовании когерентного обнаружения. На рис. 4.29 подобные графики приведены для многофазной передачи по каналу с гауссовым шумом при применении когерентного обнаружения. В каком направлении движется график при увеличении k (или М)? Из рис. 4.27 мы знаем, как изменяется кривая при увеличении и уменьшении вероятности ошибки. Поэтому можем сказать, что на рис. 4.28 по мере роста k график перемещается в направлении уменьшения вероятности ошибки. На рис. 4.29 рост k приводит к увеличению вероятности ошибки. Подобное передвижение свидетельствует, что М-арная передача сигналов уменьшает вероятность ошибки при ортогональной передаче сигналов и увеличивает — при многофазной передаче. Справедливо ли это? Почему вообще используют многофазную модуляцию PSK, если она приводит к высокой вероятности ошибки по сравнению с бинарной PSK? Сказанное действительно справедливо, и во многих системах действительно применяется многофазная передача сигналов. Подвох был в формулировке вопроса: там подразумевалось, что зависимость вероятности ошибки от Eb/N0 является единственным критерием качества. На самом деле существует множество других характеристик (например, ширина полосы, пропускная способность, сложность, стоимость), но на рис. 4.28 и 4.29 явно показана только вероятность ошибки.
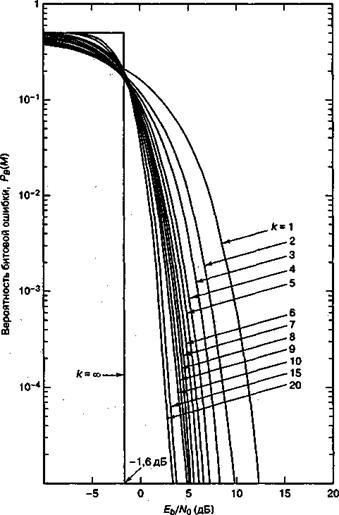
Рис. 4.28. Зависимость 
от для ортогональной М-арной передачи сигналов по каналу с гауссовым шумом при использовании когерентного обнаружения. (Перепечатано с разрешения авторов из работы W. C. Lindsey and M. K. Simon. Telecommunication System Engineering. Prentice Hall, Inc., Englewood Cliffs, N. J.)
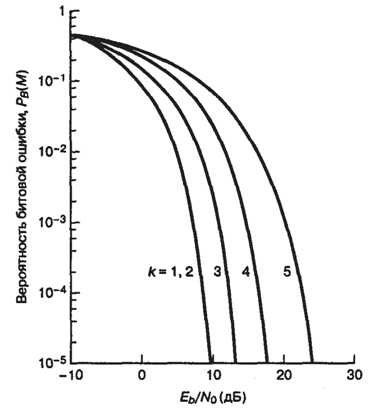
Рис. 4.29. Зависимость от для ортогональной многофазной передачи сигналов по каналу с гауссовым шумом при использовании когерентного обнаружения
Одной из рабочих характеристик, не представленных на рис. 4.28 и 4.29 явно, является необходимая ширина полосы. Для графиков на рис. 4.28 повышение значений k подразумевает увеличение требуемой ширины полосы. Для М-арных многофазных кривых, приведенных на рис. 4.29, рост величины k позволяет получать большую скорость передачи битов при той же ширине полосы. Другими словами, при фиксированной скорости передачи данных уменьшается необходимая полоса. Следовательно, графики вероятности ошибки и при ортогональной, и при многофазной передаче показывают, что М-арная передача сигналов представляет средство реализации компромиссов между параметрами системы. При ортогональной передаче сигналов повышение достоверности передачи может быть получено за счет расширения полосы. В случае многофазной передачи эффективность использования полосы может быть получена за счет вероятности ошибки.
4.8.3. Векторное представление сигналов MPSK
На рис. 4.30 показаны наборы сигналов MPSK для М - 2, 4, 8 и 16. На рис. 4.30, а видим бинарные (k=l, M = 2) антиподные векторы s, и s2, угол между которыми равен 180°. Граница областей решений разделяет сигнальное пространство на две области. На рисунке также показан вектор шума n, равный по амплитуде сигналу 
. При указанных направлении и амплитуде энергия вектора шума является минимальной, и детектор может допустить символьную ошибку.
На рис. 4.30, б видим 4-арные (k = 2, М = 4) векторы, расположенные друг к другу под углом 90°. Границы областей решений (на рисунке изображена только одна) делят сигнальное пространство на четыре области.
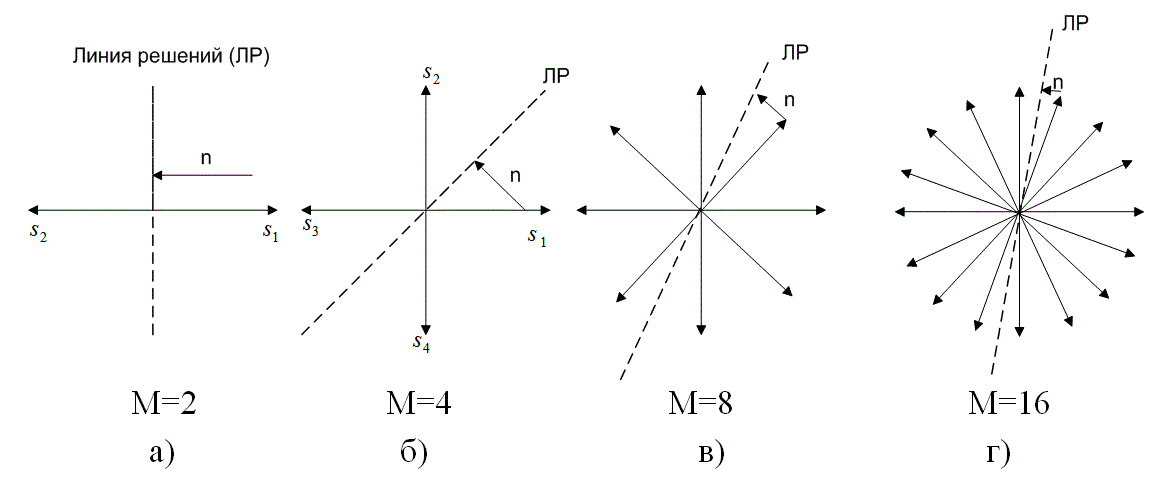
Рис. 4.30. Наборы сигналов MPSK для М = 2, 4, 8, 16
Здесь также изображен вектор шума n (начало — в вершине вектора сигнала, направление перпендикулярно ближайшей границе областей решений), являющийся вектором минимальной энергии, достаточной, чтобы детектор допустил символьную ошибку. Отметим, что вектор шума минимальной энергии на рис. 4.30, б меньше вектора шума на рис. 4.30, а, что свидетельствует о большей уязвимости 4-арной системы к шуму, по сравнению с бинарной (энергии сигналов в обоих случаях взяты равными). Изучая рис. 4.30, в, г, можно отметить следующую закономерность. При многофазной передаче сигналов по мере роста величины М на сигнальную плоскость помещается все больше сигнальных векторов. По мере того как векторы располагаются плотнее, для появления ошибки вследствие шума требуется все меньше энергии.
С помощью рис. 4.30 можно лучше понять поведение зависимости вероятности РВ от , изображенной на рис. 4.29, при росте k. Кроме того, рисунок позволяет взглянуть на природу компромиссов при многофазной передаче сигналов. Размещение большего числа векторов сигналов в сигнальном пространстве эквивалентно повышению скорости передачи данных без увеличения системной ширины полосы (все векторы ограничиваются одной и той же плоскостью). Другими словами, мы повысили использование полосы за счет вероятности ошибки. Рассмотрим рис. 4.30, г, где из приведенных вариантов вероятность ошибки является наивысшей. Чем мы может заплатить, чтобы "выкупить" возросшую вероятность ошибки? Иными словами, чем мы можем поступиться, чтобы расстояние между соседними векторами сигналов на рис. 4.30, д стало таким же, как на рис. 4.30, al Мы можем увеличивать интенсивность сигнала (сделать векторы сигналов длиннее), пока минимальное расстояние от вершины вектора сигнала до линии решений не станет равным размеру вектора шума на рис. 4.30, а. Таким образом, для многофазной системы по мере роста М мы можем увеличивать производительность полосы либо за счет повышения вероятности ошибки, либо за счет увеличения отношения .
Отметим, что на схемах, изображенных на рис. 4.30, а для различных значений М, все векторы имеют одинаковую амплитуду. Это равносильно утверждению, что сопоставление различных схем выполняется при фиксированном отношении 
, где 
— энергия символа. Сравнительные схемы можно сделать и при фиксированном отношении , в этом случае амплитуды векторов будут увеличиваться с ростом М. При М = 4, 8 и 16 амплитуды векторов будут, соответственно, в 
и 2 раза больше векторов для случая М = 2. Как и в предыдущем случае, с ростом М будет усиливаться восприимчивость к шуму, но она не будет такой явной, как на рис. 4.30.
4.8.4. Схемы BPSK и QPSK имеют одинаковые вероятности ошибки
В уравнении (3.30) было получено следующее соотношение между 
.
(4.101)
Здесь S — средняя мощность сигнала, a R — скорость передачи битов. Вероятность ошибки в сигнале BPSK с отношением , найденным из уравнения (4.101), определяется из кривой на рис. 4,29, соответствующей k = 1. Схему QPSK можно описать с помощью двух ортогональных каналов BPSK. Поток битов QPSK обычно разбивается на четный и нечетный (синфазный и квадратурный) потоки; каждый новый поток модулирует ортогональный компонент несущей со скоростью, вдвое меньшей скорости исходного потока. Синфазный поток модулирует член 
, а квадратурный — член 
. Если амплитуда исходного вектора QPSK была равна А, то амплитуды векторов синфазного и квадратурного компонентов равны, как показано на рис. 4.31, 
. Следовательно, на каждый квадратурный сигнал BPSK приходится половина средней мощности исходного сигнала QPSK. Значит, если исходный сигнал QPSK имел скорость R бит/с и среднюю мощность S Вт, квадратурное разбиение приводит к тому, что каждый сигнал BPSK имеет скорость передачи R/2 бит/с и среднюю мощность S/2 Вт.
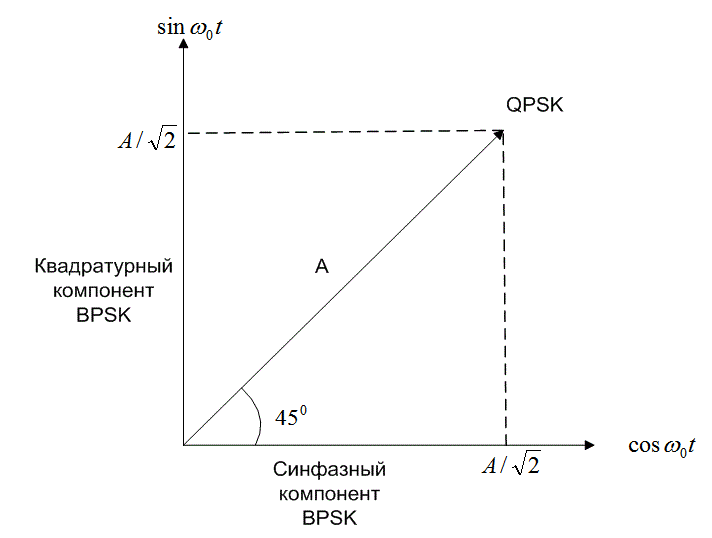
Рис. 4.31. Синфазный и квадратурный компоненты (модуляция BPSK) вектора QPSK
Следовательно, отношение , характеризующее оба ортогональных канала BPSK, создающих сигнал QPSK, эквивалентно отношению в уравнении (4.101), поскольку его можно записать точно так же.
(4.102)
Таким образом, каждый из ортогональных каналов BPSK, а следовательно, и составной сигнал QPSK характеризуются одним отношением , а значит — такой же вероятностью РВ, что и сигнал BPSK. Ортогональность (разность фаз 90°) соседних символов QPSK приводит к равным вероятностям появления ошибочного бита для схем BPSK и QPSK. Следует отметить, что вероятности появления ошибочного символа для этих схем не равны.
4.8.5. Векторное представление сигналов MFSK
В разделе 4.8.3 мы исследовали рис. 4.30, что позволило получить представление о причинах роста вероятности ошибки при увеличении числа k (или М) в схеме MPSK. Полезно будет рассмотреть подобную векторную иллюстрацию для схемы MFSK, которая позволит лучше понять графики на рис. 4.28. Поскольку сигнальное пространство MFSK описывается М взаимно перпендикулярными осями, мы без труда можем проиллюстрировать случаи М = 2 и М = 3. Итак, на рис. 4.32, а видим бинарные ортогональные векторы s1, и s2. Граница областей решений разбивает сигнальное пространство на две области. На рисунке также показан вектор шума n, представляющий минимальный вектор, который может привести к принятию неправильного решения.
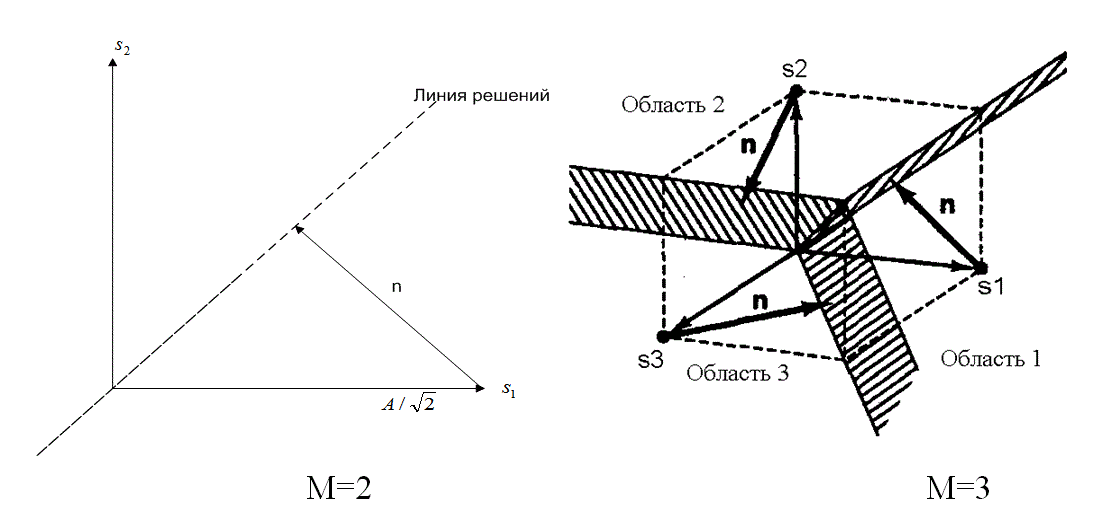
Рис. 4.32. Наборы сигналов MFSK для М = 2,3
На рис. 4.32, б показано трехмерное сигнальное пространство со взаимно перпендикулярными координатными осями. В этом случае плоскости решений разбивают пространство на три области. Показано, как к каждому сигнальному вектору 
прибавляется вектор шума n, представляющий минимальный вектор, который может привести к принятию неправильного решения. Векторы шума на рис. 4.32, б имеют тот же модуль, что и вектор шума, показанный на рис. 4.32, а. В разделе 4.4.4 мы утверждали, что при данном уровне принятой энергии расстояние между любыми двумя векторами сигналов-прототипов si и sj, М-мерного ортогонального пространства является константой. Отсюда следует, что минимальное расстояние между вектором сигнала-прототипа и любой границей решений не меняется с изменением М. В отличие от модуляции MPSK, когда добавление нового сигнала к сигнальному множеству делало сигналы более уязвимыми к меньшим векторам шума, при MFSK такого не происходит.
Дляиллюстрации этого момента можно было бы нарисовать ортогональные пространства высших размерностей, но, к сожалению, это затруднительно. Мы можем использовать только наш "мысленный взгляд", чтобы понять, что увеличение сигнального множества М — путем введения дополнительных осей, причем каждая новая ось перпендикулярна всем существующим — не приводит к его уплотнению. Следовательно, переданный сигнал, принадлежащий ортогональному набору, не становится более уязвимым к шуму при увеличении размерности. Фактически, как можно видеть из рис. 4.28, 4.28, при увеличении k вероятность появления ошибочного бита даже уменьшается.
Пониманию улучшения надежности при ортогональной передаче сигналов, показанного на рис. 4.28, способствует сравнение зависимости вероятности символьной ошибки (РЕ) от ненормированного отношения сигнал/шум (signal-to-noise ratio — SNR) с зависимостью РЕот еь/nq. На рис. 4.33 для когерентной передачи сигналов FSK представлено несколько зависимостей РЕот нормированного SNR. Видим, что ре падает с ростом М. Можем ли мы сказать, что сигнал из ортогонального набора не становится более уязвимым к данному шуму при увеличении размерности ортогонального набора? Для ортогональной передачи сигналов справедливо утверждение, что при данном SNR вектора шума фиксированного размера достаточно для перевода переданного сигнала в область ошибок; следовательно, сигналы не становятся более уязвимыми к меньшим векторам шума при увеличении М. В то же время при росте М вводится большее число окрестных областей решений; следовательно, увеличивается число возможностей для появления символьной ошибки, всего существует (М- 1) возможностей допустить ошибку. На рис. 4.33 отражено ухудшение РЕв зависимости от ненормированного SNR при увеличении М. Стоит отметить, что изучение зависимости достоверности передачи от М при фиксированном SNR не является лучшим направлением в цифровой связи. Фиксированное SNR означает фиксированный объем энергии на символ; следовательно, при увеличении М этот объем энергии необходимо распределять уже между большим числом битов, т.е. на каждый бит приходится меньше энергии. В этой связи наиболее удобным способом сравнения различных цифровых систем является использование в качестве критерия отношения сигнал/шум, нормированного на бит, или . Повышение достоверности передачи с увеличением М (см. рис. 4.28) проявляется только в том случае, если вероятность ошибки изображается как зависимость от . В этом случае при увеличении М отношение , требуемое для получения заданной вероятности ошибки, снижается при фиксированном SNR; следовательно, нам нужен новый график, подобный показанному на рис. 4.28, где ось абсцисс представляет не SNR, a . На рис. 4.34 показано, как зависимость от SNR отображается в зависимость от ; видно, как графики, демонстрирующие ухудшение РЕс увеличением М (подобно представленному на рис. 4.33), преобразуются в графики, показывающие улучшение РЕс увеличением М. Само преобразование выполняется согласно соотношению, приведенному в формуле (4.101).
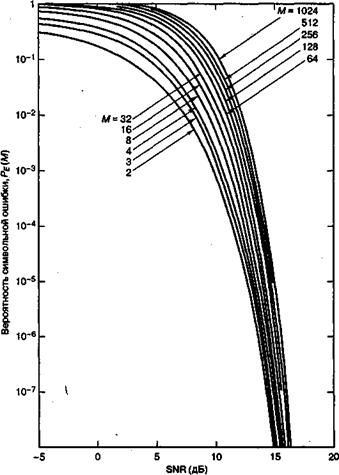
Рис. 4.33. Зависимость вероятности символьной ошибки от SNR для когерентной передани сигналов FSK. (Из документа Bureau of Standards. Technical Note 167, March, 1963; перепечатано с разрешения National Bureau of Standards из Central Radio Propagation Laboratory Technical Note 167, March, 25, 1963, Fig. 1, p. 2.)
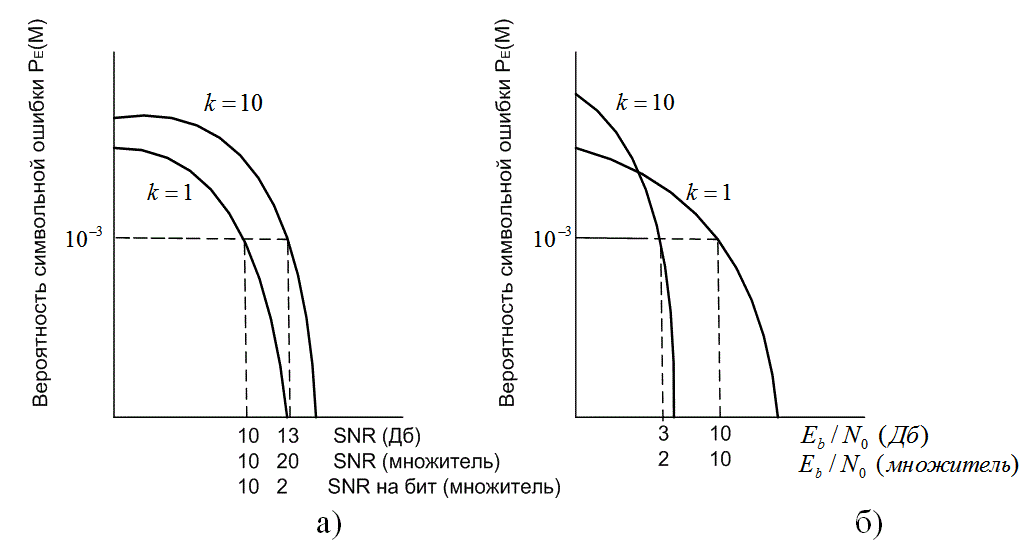
Рис. 4.34. Отображение зависимости PE от SNR в зависимость PE от для ортогональной передачи сигналов: а) ненормированная зависимость; б) нормированная зависимость
Здесь W – ширина полосы обнаружения. Поскольку
где Т – длительность символа, можем записать следующее.
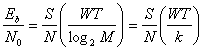(4.103)
При передаче сигналов FSK ширина полосы обнаружения W (в герцах) обычно равна скорости передачи символов 1/Т; другими словами, TW
1. Следовательно,
(4.104)
На рис. 4.34 представлено отображение зависимости РЕот SNR в зависимость РЕот для M-мерной ортогональной передачи сигналов с когерентным обнаружением; на осях показано сопоставление величин разных размерностей. На рис. 4.34, а выбрана рабочая точка, соответствующая отношению сигнал/шум = 10 дБ схемы с k= 1, при данной вероятности ошибки РЕ= 10-3. В той же системе координат приведен график схемы с k= 10; рабочая точка, соответствующая той же величине РЕ= 10-3, теперь соответствует отношению сигнал/шум, равному 13 дБ (приблизительное значение, полученное из рис. 4.33). Из приведенных графиков явно видно снижение достоверности при увеличении k. Чтобы понять, как улучшается производительность, преобразуем масштаб оси абсцисс из нелинейного (отношение сигнал/шум в децибелах) в линейный (SNR как коэффициент). На рис. 4.34, а показано, как соотносятся значения SNR в децибелах (10 и 13) со значениями, представленными как коэффициент (10 и 20), для случаев k = 1 и k = 10. Далее преобразуем масштаб оси абсцисс, чтобы единицами измерения служило отношение сигнал/шум, нормированное на бит (также выраженное как коэффициент). Этому случаю на рис. 4.34, а соответствуют величины 10 и 2 для k = 1 и k = 10. Вообще, удобно не различать 1024-ричный символ или сигнал (случай k= 10) и его 10-битовое значение. При таком подходе, если символ требует 20 единиц SNR, то 10 бит, кодирующих этот символ, требуют тех же 20 единиц; другими словами, каждый бит требует двух единиц отношения сигнал/шум.
Вместо подобного сравнения, можно просто отобразить рассматриваемые случаи k= 1 и k= 10 графиками, изображенными на рис. 4.34, б и представляющими зависимости РЕот . Случай k= 1 соответствует представленному на рис. 4.34, а. Но для случая k =10 наблюдаем разительные отличия. Видим, что при k=10 передача 10-битового символа требует всего 2 единиц (3 дБ) отношения по сравнению с 10 единицами (10 дБ) для бинарного символа. Действительно, из формулы (4.104) получаем значение отношения = 20 (1/10) = 2 (или 3 дБ), т.е. имеем повышение достоверности при увеличении k. В системах цифровой связи достоверность передачи (или вероятность ошибки) всегда выражается через , поскольку такой подход позволяет выполнять сравнение производительности различных систем. Графики, приведенные на рис. 4.33 и 4.34, а, на практике встречаются крайне редко.
Хотя изображенные на рис. 4.33 зависимости и не используются на практике часто, все же с помощью этого рисунка мы можем понять, почему ортогональная передача сигналов приводит к повышению достоверности при увеличении M или k. Рассмотрим аналогию — приобретение товара, скажем прессованного творога высшего качества. Выбор качества соответствует выбору точки на оси РЕрис. 4.33, скажем 10-3. Проведем из этой точки горизонтальную линию через все кривые (от M=2 до М = 1024). В бакалейно-гастрономическом отделе мы покупаем самую маленькую упаковку прессованного творога, которая содержит 2 унции и стоит $1. Обращаясь к рис.4.33, можем сказать, что такая покупка соответствует пересечению проведенной горизонтальной линии с графиком для М =2. Смотрим вниз на соответствующее значение параметра SNR и называем пересечение с этой осью ценой $1. При следующем походе за покупками мы решаем, что в прошлый раз стоимость творога была высокой — по 50 центов за унцию. Поэтому решаем купить большую упаковку (8 унций) за $2. Обращаемся к рис.4.33 и видим, что данная покупка соответствует пересечению горизонтальной линии с кривой М = 8. Смотрим вниз и называем соответствующее значение SNR ценой $2. Замечаем, что хотя мы и купили большую емкость, заплатив за нее большую цену, все же стоимость одной унции упала (и составляет теперь всего 25 центов). Эту аналогию можно продолжать; мы можем приобретать все большие и большие упаковки, при этом их цена (SNR) будет расти, а стоимость за унцию будет падать. Вообще, это известно давно и называется эффектом масштаба: приобретение за раз большого количества товара соответствует закупкам по оптовым ценам; при этом цена единицы товара падает. Подобным образом при использовании ортогональной передачи сигналов с символами, содержащими большее число бит, нам требуется большая мощность (большее отношение SNR), а требования относительно бита () при этом снижаются.