14.2. Секретность системы шифрования

Категория: 14. Шифрование и дешифрование

14.2.1. Совершенная секретность

14.2.2. Энтропия и неопределенность

14.2.3. Интенсивность и избыточность языка

14.2.4. Расстояние единственности и идеальная секретность

14.2.1. Совершенная секретность

Рассмотрим систему шифрования с конечной областью сообщений {М}= М0, М1 ..., MN-1 и конечной областью шифрованных текстов {С} = С0, С1 ..., CU-1,. Для любого Мi априорная вероятность передачи сообщения Мi, равна Р(Мi). Апостериорная вероятность принятия сообщения Cj при переданном сообщении М, равна P(Мi/Cj). Говорят, что система шифрования имеет совершенную секретность, если для любого сообщения Mi и любого шифрованного текста Cj апостериорная вероятность равна априорной.

(14.2)

Таким образом, для системы с совершенной секретностью характерно следующее: если криптоаналитик перехватил сообщение Cj, то дальнейшей информации, которая бы облегчила ему дешифровку сообщения, он не получит. Необходимое и достаточное условие совершенной секретности: для любого Mi и Cj,

(14.3)

На рис. 14.4 изображен пример схемы совершенной секретности. В этом примере {М}=М0, М1, М2, М3; {С} = С0, С1,С2, С3; {К} =K0, K1 K2,K3 ;N=U=4, Р(Мi)=Р(Сj) =1/4.

Преобразование сообщения в шифрованный текст выполняется следующим образом.

(14.4)

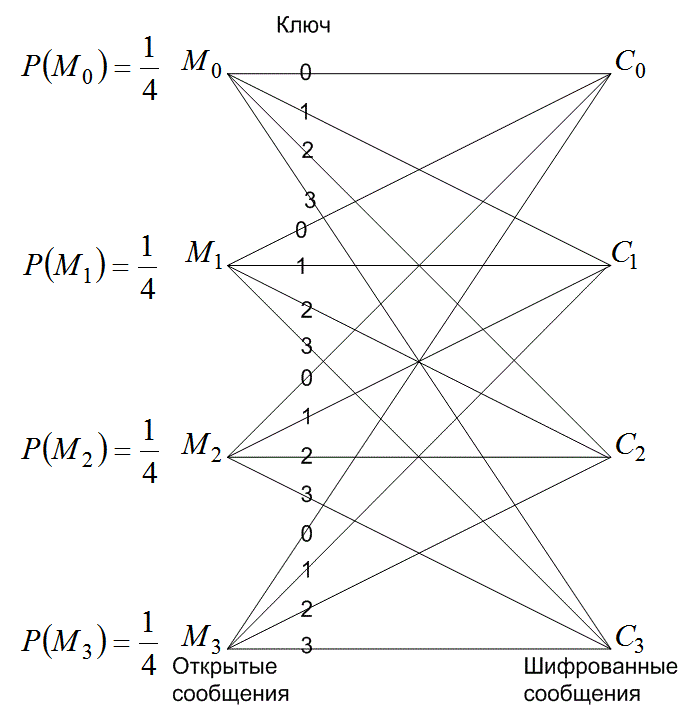
Рис.14.4. Совершенная секретность.

Здесь ТKj определяет преобразование с помощью ключа Kj, а «х по модулю y»— это остаток от деления х на y. Таким образом, s= 0, 1, 2, 3. Криптоаналитик, перехвативший одно из шифрованных сообщений Cs =С1, С1,С2или С3, не сможет определить, какой из четырех ключей использовался и, следовательно, какое из сообщений М0, М1, М2или М3является верным. Если в системе шифрования число сообщений, число ключей и число шифрованных сообщений равны между собой, то система имеет совершенную секретность тогда и только тогда, когда выполняются следующие два условия.

1. Существует только один ключ, преобразующий каждое сообщение в каждый шифрованный текст.

2. Все ключи равновероятны.

Если эти условия не выполняются, то будет существовать некоторое сообщение Мi , при котором для данного Сj, не существует ключа, который мог бы дешифровать Сj в Мi. Отсюда следует, что для некоторых i и j Р(Мi/Сj)=0. В этом случае криптоаналитик может исключить из рассмотрения определенные нешифрованные сообщения, упростив, таким образом, задачу. Вообще, совершенная секретность является очень желательным свойством, поскольку это означает, что система шифрования безусловно защищена. Должно быть очевидно, что в системах, передающих большое количество сообщений, для достижения совершенной секретности требуется распределить большое количество ключей, а это, в свою очередь, может привести к значительным практическим затруднениям, что делает такие системы нереализуемыми. В системе с совершенной секретностью число возможных ключей так же велико, как и число возможных сообщений, поэтому, если мы разрешим передавать сообщения неограниченной длины, совершенная секретность потребует бесконечного количества ключей.

Пример 14.1. Взлом системы шифрования, если область ключей меньше области сообщений

Рассмотрим шифрованный текст, состоящий из 29 символов.

G R O В О К В О D R O R O В Y O C Y P I O C D O B I O K B

Данный текст был получен с помощью шифра Цезаря (см. раздел 14.1.4); каждая буква получена сдвигом на K символов, где 1К25. Покажите, как криптоаналитик может взломать этот код.

Решение

Поскольку количество возможных ключей (их 25) меньше количества возможных осмысленных сообщений из 29 символов (их огромное множество), совершенная секретность не может быть достигнута. В исходном полиалфавитном шифре, показанном на рис. 14.3, символ открытого текста заменяется буквой некоторой строки, причем номер строки постоянно возрастает. Следовательно, в процессе анализа шифрованного текста мы обращаем процесс: теперь буквы шифрованного текста заменяются буквами строк, причем номер строки постоянно уменьшается. Путем перебора всех ключей от 1 до 25 (рис. 14.5) можно легко рассмотреть все возможности. В результате, этот процесс приводит к единственному ключу (K=10), дающему осмысленное сообщение (пробелы были добавлены вручную): WHERE ARE THE HEROES OF YESTERYEAR.

Пример 14.2. Совершенная секретность

Для создания шифра, имеющего совершенную секретность, можно несколько модифицировать область ключей, описанную в примере 14.1. В этой новой системе шифрования каждый символ сообщения шифруется с использованием случайно выбранного ключевого значения. Теперь ключ K задается последовательностью k1, k2, ..., k29, где каждое ki— это случайно выбранное целое число из интервала (1,25), определяющее сдвиг, используемый для i-го символа. Таким образом, всего существует (25)29 различных ключевых последовательностей. Значит, шифрованный текст из 29 символов, приведенный в примере 14.1, может соответствовать любому осмысленному сообщению из 29 символов. Например, шифрованный текст мог соответствовать следующему открытому тексту (пробелы были добавлены вручную).

ENGLISH AND FRENCH ARE SPOKEN HERE

Данный текст получен с помощью ключа 2, 4, 8, 16, 6, 18, 20, ... . Стоит отметить, что большинство возможных наборов из 29 символов можно исключить, поскольку они не являются осмысленными сообщениями. Совершенная секретность данного кода – результат того, что перехват шифрованного текста не дает никакой дополнительной информации об открытом сообщении.

Ключ Текст

0

G

R

O

B

O

K

B

O

D

R

O

R

O

B

Y

O

C

Y

P

I

O

C

D

O

B

I

O

K

B

1

F

Q

N

A

N

J

A

N

C

Q

N

Q

N

A

X

N

B

X

O

H

N

B

C

N

A

H

N

J

A

2

E

P

M

Z

M

I

Z

M

B

P

M

P

M

Z

W

M

A

W

N

G

M

A

B

M

Z

G

M

I

Z

3

D

O

L

Y

L

H

Y

L

O

A

L

O

L

Y

V

L

Z

V

M

F

L

Z

A

L

Y

F

L

H

Y

4

C

N

K

X

K

G

X

K

Z

N

K

N

K

X

U

K

Y

U

L

E

K

Y

Z

K

X

E

K

G

X

5

B

M

J

M

J

F

W

J

Y

M

J

M

J

W

T

J

X

T

K

D

J

X

Y

J

W

D

J

F

W

6

A

L

I

V

I

E

V

I

X

L

I

L

I

V

S

I

W

S

J

C

I

W

X

I

V

C

I

E

V

7

Z

K

H

U

H

D

U

H

W

K

H

K

H

U

R

H

V

R

I

B

H

V

W

H

U

B

H

D

U

8

Y

J

G

T

G

C

T

G

V

J

G

J

G

T

Q

G

U

Q

H

A

G

U

V

G

T

A

G

C

T

9

X

I

F

S

F

B

S

F

U

I

F

I

F

S

P

F

T

P

G

Z

F

T

U

F

S

Z

F

B

S

10

W

H

E

R

E

A

R

E

T

H

E

H

E

R

O

E

S

O

F

Y

E

S

T

E

R

Y

E

A

R

11

V

G

D

Q

D

Z

Q

D

S

G

D

G

D

Q

N

D

R

N

E

X

D

R

S

D

Q

X

D

Z

Q

12

U

F

C

P

C

Y

P

C

R

F

C

F

C

P

M

C

Q

M

D

W

C

Q

R

C

P

W

C

Y

P

13

T

E

B

O

B

X

O

B

Q

E

B

E

B

O

L

B

P

L

C

V

B

P

Q

B

O

V

B

X

O

14

S

D

A

N

A

W

N

A

P

D

A

D

A

N

K

A

O

K

B

U

A

O

P

A

N

U

A

W

N

15

R

C

Z

M

Z

V

M

Z

O

C

Z

C

Z

M

J

Z

N

J

A

T

Z

N

O

Z

M

T

Z

V

M

16

Q

B

Y

L

Y

U

L

Y

N

B

Y

B

Y

L

I

Y

M

I

Z

S

Y

M

N

Y

L

S

Y

U

L

17

P

A

X

K

X

T

K

X

M

A

X

A

X

K

H

X

L

H

Y

R

X

L

M

X

K

R

X

T

K

18

O

Z

W

J

W

S

J

W

L

Z

W

Z

W

J

G

W

K

G

X

Q

W

K

L

W

J

Q

W

S

J

19

N

Y

U

H

U

Q

H

U

J

X

U

X

U

H

E

U

I

E

V

O

U

I

J

U

H

O

U

Q

H

20

M

X

U

H

U

Q

H

U

J

X

U

X

U

H

E

U

I

E

V

O

U

I

J

U

H

O

U

Q

H

21

L

W

T

G

T

P

G

T

I

W

T

W

T

G

D

T

H

D

U

N

T

H

I

T

G

N

T

P

G

22

K

V

S

F

S

O

F

S

H

V

S

V

S

F

C

S

G

C

T

M

S

G

H

S

F

M

S

O

F

23

J

U

R

E

R

N

E

R

G

U

R

U

R

E

B

R

F

B

S

L

R

F

G

R

E

L

R

N

E

24

I

T

Q

D

Q

M

D

Q

F

T

Q

T

Q

D

A

Q

E

A

R

K

Q

E

F

Q

D

K

Q

M

D

25

H

S

P

C

P

L

C

P

E

S

P

S

P

C

Z

P

D

Z

Q

J

P

D

E

P

C

J

P

L

C

Рис. 14.5. Пример взлома системы шифрования, если область ключей меньше области сообщений

14.2.2. Энтропия и неопределенность

Объем информации в сообщении связан с вероятностью появления сообщения. Сообщения вероятности 0 либо 1 не содержат информации, поскольку можно с известной долей определенности предсказать их появление. Чем больше неопределенности существует в предсказании появления сообщения, тем больше оно содержит информации. Следовательно, если все сообщения множества равновероятны, мы не можем быть уверенными в возможности предсказания появления конкретного сообщения, и неопределенность информационного содержания сообщения является максимальной.

Энтропия Н(К) определяется как средний объем информации на сообщение. Она может рассматриваться как мера того, насколько в выбор сообщения X вовлечен случай. Она записывается как следующее суммирование по всем возможным сообщениям.

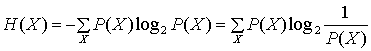(14.5)

Если, как выше, логарифм берется по основанию 2, Н(Х) представляет собой математическое ожидание числа битов в оптимально закодированном сообщении X. Это все еще не та мера, которую хотел бы иметь криптоаналитик. Им будут перехвачены некоторые шифрованные тексты, и он захочет узнать, насколько достоверно он может предсказать сообщение (или ключ) при условии, что был отправлен именно этот конкретный шифрованный текст. Неопределенность, определенная как условная энтропия X при данном Y, является для криптоаналитика более полезной мерой при попытке взлома шифра. Она задается с помощью следующей формулы.

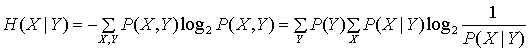(14.6)

Неопределенность может рассматриваться как неуверенность в том, что отправлено было сообщение X, при условии получения Y. Желательным для криптоаналитика является приближение H(X|Y) к нулю при увеличении объема перехваченного шифрованного текста Y.

Пример 14.3. Энтропия и неопределенность

Рассмотрим выборочное множество сообщений, состоящее из восьми равновероятных сообщений {X} = Х1, Х2, ... Х8.

а) Найдите энтропию, связанную с сообщением из множества {X}.

б) Дано другое множество равновероятных сообщений {Y}=Y1, Y2. Пусть появление каждого сообщения Y сужает возможный выбор X следующим образом.

При наличии Y1 возможны только Х1, Х2, Х3или Х4

При наличии У2 возможны только Х5, Х6, Х7 или Х8

Найдите неопределенность сообщения X, обусловленную сообщением Y.

Решение

а) Р(Х)=

Н(Х) = 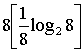= 3 бит/сообщение

б) Р(Y)=. Для каждого Y, P(X|Y)=для четырех сообщений из множества {X} и P(X|Y)=0 для оставшихся четырех. Используя уравнение (14.6), получим следующее.

H(X|Y)=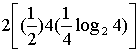= 2 бит/сообщение

Видно, что знание Y сводит неопределенность X с 3 бит/сообщение до 2 бит/сообщение.

14.2.3. Интенсивность и избыточность языка

Истинная интенсивность языка определяется как среднее число информационных битов, содержащихся в каждом символе, и для сообщения длиной N выражается следующим образом.

(14.7)

Здесь Н(Х) — энтропия сообщения, или число битов в оптимально закодированном сообщении. Для письменного английского языка при больших N оценки r дают значения между 1,0 и 1,5 бит/символ [4]. Абсолютная интенсивность или максимальная энтропия языка определяется как максимальное число информационных битов, содержащихся в каждом символе, в предположении, что все возможные последовательности символов одинаково вероятны. Абсолютная интенсивность задается следующим образом.

r' = log2L (14.8)

Здесь L - число знаков в языке. Для английского алфавита r'=log226 = =4,7 бит/символ. Истинная интенсивность английского языка, конечно, гораздо меньше его абсолютной интенсивности, поскольку, как и большинство языков, английский очень избыточен и структурирован.

Избыточность языка определяется через его истинную и абсолютную интенсивности.

D = r '- r (14.9)

Для английского языка, где r'=4,7 бит/символ и r=1,5 бит/символ, D= 3,2, а отношение D/r'= 0,68 - это мера избыточности языка.

14.2.4. Расстояние единственности и идеальная секретность

Ранее утверждалось, что если допускаются сообщения неограниченной длины, то совершенная секретность требует бесконечного количества ключей. При конечном размере ключа его неопределенность Н(К|С) обычно приближается к нулю, откуда следует, что ключ может быть определен единственным образом, а система шифрования может быть взломана. Расстояние единственности (unicity distance) определяется как наименьшая длина шифрованного текста N, при которой неопределенность ключа Н(К|С) близка к нулю. Следовательно, расстояние единственности — это количество шифрованного текста, необходимое для того, чтобы однозначно определить ключ и таким образом взломать систему шифрования. Шеннон (Shennon) [5] описал систему с идеальной секретностью как систему, в которой Н(К|С) не стремится к нулю, если количество шифрованного текста стремится к бесконечности. Иными словами, ключ не может быть определен, независимо от того, сколько шифрованного текста перехвачено. Термин «идеальная секретность» описывает систему, которая не достигает совершенной секретности, но, тем не менее, не поддается взлому (безусловно защищенная система), поскольку она не дает достаточно информации для определения ключа.

Большинство систем шифрования слишком сложны для определения вероятностей, необходимых для вычисления расстояния единственности. В то же время расстояние единственности иногда можно аппроксимировать, что было показано Шенноном [5] и Хэллманом (Hellman) [6]. Следуя Хэллману, предположим, что каждый открытый текст и шифрованное сообщение получены с помощью конечного алфавита из L символов. Таким образом, всего существует 2r’N возможных сообщений длиной N, где r’ — абсолютная интенсивность языка. Всю область сообщений можно разделить на два класса - осмысленные сообщения M1 и бессмысленные сообщения М2. Тогда имеем

число осмысленных сообщений 2r’N (14.10)

число бессмысленных сообщений 2r’N - 2rN, (14.11)

где r — истинная интенсивность языка, а априорные вероятности классов сообщений описываются следующими выражениями.

M1 – осмысленное (14.12)

Р(М2) = 0 М2 – бессмысленное (14.13)

Предположим, что существует 2H(K) возможных ключа (размер алфавита ключей), где H(К) — энтропия ключа (бит в ключе). Предположим, что все ключи равновероятны.

Р(К) == 2-Н(К) (14.14)

Определение расстояния единственности основано на модели случайного шифра, которая утверждает, что для каждого ключа К и шифрованного текста С операция дешифрования DK(С) дает независимую случайную переменную, распределенную по всем возможным 2r’N сообщениям (как осмысленным, так и бессмысленным). Следовательно, для данных К и С операция DK(С) может с равной вероятностью давать любое из открытых сообщений.

При данном шифровании, описываемом как Сi=EKi(Mi), неверное решение F возникает всегда, когда шифрование с помощью другого ключа Kj может давать Сi из того же сообщения Mi или из некоторого другого сообщения Мj.

Ci=EKi(Mi) = EKj(Mi) = EKj(Mj) (14.15)

Криптоаналитик, перехвативший Сi, не сможет выбрать верный ключ и, следовательно, не сможет взломать систему шифрования. Мы не рассматриваем операции дешифрования, которые дают бессмысленные сообщения, так как они могут легко отбрасываться.

Для каждого верного решения конкретного шифрованного текста существует 2H(K)-1 неверных ключа, каждый из которых имеет ту же вероятность P(F) получения неверного решения. Так как все осмысленные открытые сообщения предполагаются равновероятными, вероятность неверного решения равна вероятности получения осмысленного сообщения.

P(F)== 2(r-r’) = 2 -DN (14.16)

Здесь D =r’-r — избыточность языка. Тогда ожидаемое число неверных решений F равно следующему.

(14.17)

Поскольку F быстро убывает с увеличением N, то

log2 = H(K)-DN= 0 (14.18)

является точкой, где число неверных решений достаточно мало; так что шифр может быть взломан. Следовательно, получаемое расстояние единственности описывается следующим выражением.

N= (14.19)

Из уравнения (14.17) следует, что если Н(К) значительно больше DN, то будет множество осмысленных расшифровок, и, следовательно, существует малая вероятность выделения криптоаналитиком верного сообщения из возможных осмысленных. Приблизительно, DN — это число уравнений для ключа, а Н(К) — число неизвестных. Если число уравнений меньше числа неизвестных битов ключа, единственное решение невозможно; говорят, что система не поддается взлому. Если число уравнений больше числа неизвестных, возможно единственное решение, и система не может больше считаться не поддающейся взлому (хотя она все еще может относиться к защищенным по вычислениям).

Стоит отметить, что доминирование бессмысленных дешифровок позволяет взламывать криптограммы. Уравнение (14.19) показывает значение использования сжатия данных до шифрования. Сжатие данных устраняет избыточность языка, таким образом, увеличивая расстояние единственности. Совершенное сжатие данных даст D = 0 и N =для любого размера ключа.

Пример 14.4. Расстояние единственности

Вычислите расстояние единственности для системы шифрования, использующей письменный английский язык, ключ которой задается последовательностью k1, k2,..., k29, где каждое ki — случайное целое из интервала (1, 25), которое определяет номер сдвига (рис. 14.3) для i-го символа. Предположим, что все возможные ключевые последовательности равновероятны.

Решение

Существует (25)29 возможных равновероятных ключевых последовательностей. Следовательно, используя равенства (14.5), (14.8) и (14.19), получаем следующее.

Энтропия ключа: Н(К) = log2 (25)29 =135 бит

Абсолютная интенсивность английского языка: r’=log226= 4,7 бит/символ

Предполагаемая истинная интенсивность английского языка:

r=1,5 бит/символ

Избыточность: D = r’-r = 3,2 бит/символ

N =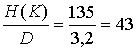 символа

В примере 14.2 совершенная секретность сообщения из 29 символов иллюстрировалась с использованием того же типа ключевой последовательности, что и в данном примере, где показано, что если имеющийся шифрованный текст состоит из 43 символов (откуда следует, что некоторая часть ключевой последовательности должна использоваться дважды), то возможно единственное решение. В то же время не определена вычислительная сложность отыскания решения. Даже если оценить теоретическое количество шифрованного текста, необходимое для взлома шифра, практически это может оказаться невозможным.