4.1. Кривые второго порядка. Окружность

4.2. Эллипс

4.3. Гипербола

4.4. Парабола

4.1. Кривые второго порядка

Геометрическое место точек называется алгебраической кривой, если левая часть его уравнения в декартовых координатах после упрощения и переноса всех членов в одну часть равенства будет многочленом относительно x и y. Степень этого многочлена, т. е. наибольшая из сумм показателей степеней x и y членов многочлена, называется порядком этой кривой. Можно доказать (это будет ниже доказано только для кривых второго порядка), что порядок алгебраической кривой не зависит от выбора осей координат на плоскости; иными словами, степень уравнения данной кривой остается одной и той же, к какой бы системе прямоугольных координат ее ни относить.

Всякое уравнение вида , т. е. уравнение первой степени относительно x и y, всегда определяет на плоскости некоторую прямую; таким образом, кривые первого порядка – это прямые линии.

К кривым второго порядка относятся эллипс, частным случаем которого является окружность, гипербола и парабола. Кроме того, в некоторых случаях уравнение второй степени относительно x и y может определять две прямые, точку или мнимое геометрическое место.

Кривые второго порядка – эллипс, гипербола и парабола – играют большую роль в прикладных вопросах. Напомним, что планеты солнечной системы в соответствии с первым законом Кеплера движутся вокруг Солнца по эллипсам; по эллипсам же движутся вокруг планет их спутники (в частности, искусственные спутники Земли); наконец, кометы, зашедшие в солнечную систему из мирового пространства, могут двигаться вокруг Солнца либо по эллипсам, либо по параболам, либо по гиперболам в зависимости от значения скорости, с которой комета приближается к Солнечной системе.

Кривые второго порядка начнем изучать с простейших из них – окружности.

Окружность

Как известно, уравнение окружности радиуса с центром в точке имеет вид:

(3.1).

Если в этом уравнении раскрыть скобки и перенести в левую часть равенства, то уравнение примет вид:

(3.1`).

Геометрический смысл уравнения не изменится, если все его члены умножить на один и тот же, отличный от нуля и не зависящий от и множитель ;
введем обозначения – ,
– , .

Уравнение (3.1') запишется тогда в виде:

(3.2).

Возникает вопрос: всякое ли уравнение вида (3.2) является уравнением некоторой окружности?

Чтобы ответить на этот вопрос, проделаем обратное преобразование уравнения (3.2) к виду (3.1), считая коэффициенты A, D, E и F произвольными (но ).

Разделим все члены уравнения (3.2) на А и введем обозначения: , , ; тогда уравнение (3.2) примет вид:

(3.2`).

Дополняя члены с x и y до полных квадратов и перенося член направо, придадим уравнению (3.2') вид:

(3.3).

Правая часть последнего уравнения может быть числом положительным, отрицательным или нулем.

1. Если , то положим .

Уравнение (3.3) запишется в виде:

(3.3`)

и является, как известно, уравнением окружности радиуса R с центром в точке .

2. Если , то уравнение (3.3) принимает вид:

(3.3``).

Ему удовлетворяют только значения , (сумма двух квадратов может быть равна нулю только тогда, когда одновременно равен нулю каждый из них); таким образом, уравнению (3.3'') удовлетворяет единственная точка плоскости .
Но, впрочем, можно говорить, что уравнение (3.3'') и в этом случае является уравнением окружности, но окружности, выродившейся в точку (окружности с нулевым радиусом).

3. Если , то полагая , приводим уравнение (3.3) к виду:

(3.3```).

Поскольку сумма квадратов двух вещественных чисел не может быть числом отрицательным, то на плоскости xOy не существует точек, которые удовлетворяли бы уравнению (3.3''').
Поэтому уравнение (3.3''') не определяет никакой кривой; иногда говорят, впрочем, что уравнение (3.3''') является уравнением мнимой окружности.

Только учитывая это последнее замечание, можно говорить, что уравнение (3.2) всегда определяет окружность (вещественную, выродившуюся в точку или мнимую).

Примеры.

1. Уравнение x² + y² – 4x + 6y – 12 = 0 приводится к виду (x – 2)² + (y + 3)² = 25 и определяет окружность радиуса R = 5 с центром в точке С(2;–3).

2. Уравнение x² + y² + 2x + 1 = 0 приводится к виду (x + 1)² + y² = 0 и определяет единственную точку С(–1;0).

3. Уравнение x² + y² + 4x + 2y + 7 = 0 приводится к виду (x + 2)² + (y + 1)² = – 2 и никакой вещественной кривой не определяет (мнимая окружность).

4.2. Эллипс

Эллипсом называется геометрическое место точек плоскости, сумма расстояний которых от двух данных точек этой же плоскости, называемых фокусами эллипса, постоянна.

Пусть фокусами эллипса являются точки F₁ и F₂, а М – некоторая точка, принадлежащая эллипсу. По определению эллипса для любой его точки М имеем:

(3.4)

где через обозначена упоминаемая в определении эллипса постоянная величина. Введем обозначение ; очевидно, что ( – сумма двух сторон треугольника , а – его третья сторона).

Для вывода простейшего уравнения эллипса выберем следующее расположение координатных осей. Начало координат О поместим в середину отрезка , а за ось примем прямую, проходящую через фокусы и , ось направим перпендикулярно к оси в точке .

При таком выборе осей координаты фокусов будут , ; произвольную точку эллипса обозначим через .

Имеем:

, (3.5),

а подставляя эти значения в уравнение (3.4), находим:

(3.6).

Получено уравнение эллипса. Для преобразования уравнения к более простому виду перенесем корень второй степени в правую часть равенства и возведем обе части равенства в квадрат (одновременно раскрыв скобки):

(3.7).

Перенося в этом уравнении радикал в левую часть, а все остальные члены – в правую часть равенства, после привидения подобных членов и сокращения на общий множитель найдем:

(3.8).

Снова возведем в квадрат обе части уравнения:

(3.9).

Перенесем теперь члены с текущими координатами в левую часть равенства, а постоянные члены – в правую:

(3.10).

Наконец, разделим левую и правую части на :

(3.11).

Так как , то можно положить ; тогда окончательно получим следующую простейшую (ее называют канонической) форму уравнения эллипса:

(3.12).

Можно доказать, что уравнение (3.12) равносильно исходному уравнению (3.6).

Исследуем форму эллипса по его уравнению. Прежде всего заметим, что каждое из двух слагаемых левой части уравнения (3.12) не превосходит единицы, поскольку их сумма (а они оба положительны) равна единице:

, ;

отсюда найдем, что для всех точек эллипса:

, , (3.13)

т. е. что эллипс целиком лежит внутри прямоугольника, определяемого неравенствами (3.13).

Далее заметим, что уравнение (3.12) сохраняет вид, если заменить на или на (поскольку x и y входят в уравнение лишь во второй степени). Из этого следует, что если на эллипсе лежит некоторая точка , то одновременно с нею на эллипсе лежат и три точки , и , симметричные с точкой М соответственно относительно оси Ox , оси Oy и начала координат. Это означает, что эллипс имеет оси координат своими осями симметрии и поэтому для его построения достаточно построить его дугу, лежащую, например, в I четверти.

Решим уравнение (3.12) относительно y:

(3.14).

Для построения дуги эллипса, лежащей в I четверти, надо в правой части (3.14) взять знак плюс и изменять x только от 0 до a:

, (3.14`)

Из этого уравнения следует:
1) при ;
2) при возрастании x от 0 до а y убывает от b до 0; 3) при .
Это позволяет нам построить дугу эллипса, лежащую в I четверти, и по соображениям симметрии весь эллипс.

Познакомимся с принятой в аналитической геометрии по отношению к эллипсу терминологией.

Отрезки и осей симметрии эллипса, принятых нами з оси координат, называют соответственно большой и малой осями эллипса; их длины равны соответственно 2a и 2b (, так как ); половину их длин – числа a и b – часто называют большой и малой полуосями эллипса. Точка О пересечения осей симметрии эллипса называется его центром. Концы большой и малой осей эллипса – точки , , , – называют его вершинами.

Форма эллипса зависит от величины соотношения длин его малой и большой полуосей: чем больше это соотношение, тем эллипс будет менее "сплющенным", менее сжатым; при эллипс, как легко установить по его уравнению (3.12), превращается в окружность; в самом деле, в этом случае уравнение (3.12) превращается в уравнение:

(3.15),

т. е. в уравнение окружности радиуса а с центром в начале координат.

В качестве характеристики формы эллипса в аналитической геометрии чаще пользуются не соотношением его полуосей , а другой величиной – отношением половины расстояния с между фокусами эллипса к его большой полуоси а, которое называют эксцентриситетом и обозначают греческой буквой "эпсилон" ():

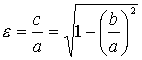(3.16).

Так как , то эксцентриситет для различных эллипсов может меняться в пределах от 0 до 1: ; чем больше эксцентриситет, тем больше расстояние от центра эллипса до его фокусов и тем более сплющен эллипс; чем ближе эксцентриситет к нулю, тем больше форма эллипса приближается к окружности. (Если положить , то эллипс превращается в окружность; если положить , эллипс превращается в свою собственную большую ось).

Если по уравнению эллипса (3.12) нужно построить не только сам эллипс, но и отметить на чертеже положение его фокусов и , то полезно запомнить. Что расстояния от фокусов эллипса до концов и его малой оси равны длине большой полуоси эллипса а:

.

Это сразу следует из основного соотношения, связывающего величины a, b и с:

(3.17).

Пример.

Найти простейшее уравнение и построить его, если его большая ось расположена на оси Ox симметрично относительно начала координат и имеет длину , а эксцентриситет эллипса .

Решение. Пользуясь формулой (3.16), находим с:

.

Затем по формуле (3.17) определяем .
Зная теперь a и b, получаем простейшее уравнение эллипса:

.

Построение этого эллипса по его уравнению рекомендуем читателю сделать самостоятельно.

Рассмотрим теперь уравнение

, в котором .

Очевидно, отнесенный к системе координат, в которой оси Ox и Oy поменялись ролями: большая ось и фокусы этого эллипса лежат на оси Oy, а малая ось – на оси Ox (рис. 3.3). Следует лишь помнить, что для такого эллипса и .
Координаты фокусов такого эллипса: и .

4.3. Гипербола

Гиперболой называется геометрическое место точек плоскости, разность расстояний которых от двух данных точек той же плоскости, называемых фокусами гиперболы, постоянна.

Для вывода простейшего уравнения гиперболы расположим оси координат по отношению к ее фокусам и так же, как мы это делали в предыдущем параграфе для эллипса. Сохраним для гиперболы те же обозначения: 2а для постоянной величины, упоминаемой в определении гиперболы, 2с для расстояния между фокусами и . Координаты фокусов те же, что и для эллипса в предыдущем параграфе: и .

Возьмем произвольную точку , лежащую на гиперболе. По определению гиперболы для точек кривой, лежащих в I и IV четвертях имеем:

(3.18),

а для точек, лежащих во II и III четвертях:

(3.18`).

Заметим, что для гиперболы в отличие от эллипса (2а есть разность двух сторон треугольника , а 2с – его третья сторона). Выражая через координаты точек , и длины отрезков и оба равенства (3.18) и (3.18') можно записать в виде:

(3.19).

Производя над этим уравнением те же преобразования, что и над уравнением (3.6) в случае эллипса (см. § 4.2), мы в конечном счете придем
к тому же самому уравнению (3.10):

,

в котором, однако, теперь .
(Рекомендуется читателю произвести это преобразование самостоятельно.)

Деля левую и правую части уравнения (3.10) на и учитывая, что теперь , запишем результат в виде:

(3.20).

Наконец, полагая , получим окончательно простейшее (каноническое) уравнение гиперболы:

(3.21).

Можно доказать, что равенство (3.21) равносильно объединенному равенству (3.19).

Для построению гиперболы по ее уравнению (3.21) заметим прежде всего, что первый член левой части этого уравнения не меньше его правой части, т. е. единицы (поскольку из вычитается неотрицательная величина ): .

Отсюда .
Таким образом, в вертикальной полосе между параллельными оси Oy прямыми и точек кривой нет.

Отмечаем далее, что, так же как и для эллипса, оси координат служат осями симметрии гиперболы, так как в уравнении (3.21) x и y входят лишь в четных степенях. Поэтому достаточно построить часть гиперболы, лежащую в I четверти.

Решим уравнение гиперболы (3.21) относительно y: ,
выберем в правой части знак плюс, поскольку в I четверти :

, (3.22).

При ; при возрастании x возрастает и y: ветвь гиперболы, подымаясь от оси Ox, уходит на плоскости все дальше и дальше, или, как говорят в геометрии, уходит "в бесконечность". Но при этом, как нетрудно показать, ветвь кривой все ближе и ближе подходит к прямой .
В самом деле, разность между ординатами точек этой прямой и гиперболы (обозначим ее через ), соответствующих одному и тому же значению абсциссы х, имеем следующее выражение:

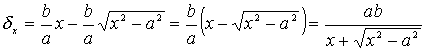(3.23)

Из последнего выражения видно, что когда х неограниченно возрастает, то , оставаясь положительным, стремится к нулю, что и подтверждает высказанную нами мысль: ветвь гиперболы, лежащая в I четверти неограниченно приближается (и притом снизу, так как ) к прямой , когда абсцисса х точки гиперболы неограниченно возрастает. Такие прямые, к которым неограниченно приближаются уходящие в бесконечность ветви кривых, называются асимптотами этих кривых.

Таким образом, прямая является асимптотой гиперболы. В силу симметрии гиперболы у нее есть и вторая асимптота: . Наличие асимптот и соображения симметрии позволяют нам построить всю гиперболу (рис. 5): кривая состоит из двух не смыкающихся ветвей, лежащих в углах между прямыми и и неограниченно приближаются к этим прямым.

В отношении гиперболы используется следующая терминология.

Отрезок называют вещественной, а – мнимой осью гиперболы; их длины равны соответственно 2а и 2b (а – вещественная полуось, b – мнимая полуось). Точки гиперболы и , лежащие на вещественной оси, – вершины гиперболы. Точка О – центр гиперболы. Изображенный на рис. 3.5 пунктиром прямоугольник с центром в точке О и сторонами , и , параллельными осями симметрии гиперболы, называют осевым прямоугольником гипербол; его построение облегчает построение гиперболы; сама гипербола касается вертикальных сторон этого прямоугольника в их серединах, являющихся вершинами гиперболы.

Для построения фокусов гиперболы и полезно знать, что основное соотношение между величинами , и у гиперболы можно записать в виде:

(3.24).

Поэтому расстояние от центра гиперболы до ее фокуса равно половине длинны диагонали осевого прямоугольника : в прямоугольном треугольнике катеты , , а следовательно, его гипотенуза .

Форма гиперболы зависит от угла наклона асимптоты к вещественной оси, т. е. от величины отношения : чем эта величина меньше, тем меньше угол между асимптотами, в котором заключена гипербола, и тем более сжата сама гипербола; чем больше величина , тем круче располагаются ветви гиперболы.

Но, так же как и для эллипса, в качестве характеристики формы гиперболы в аналитической геометрии пользуются не величиной отношения , а величиной , называемой эксцентриситетом гиперболы и обозначают той же буквой , как и для эллипса:

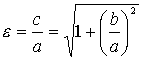(3.25).

Так как у гиперболы , то эксцентриситет гиперболы .
Из прямоугольного треугольника , в котором острый угол наклона асимптоты к вещественной оси обозначен через , находим:

и, следовательно:

(3.26),

т. е. эксцентриситет гиперболы равен секансу угла наклона асимптоты к вещественной оси.

Важным частным случаем гиперболы является равносторонняя (равноосная) гипербола – такая гипербола, у которой равны длины вещественной и мнимой полуосей: .

Уравнение этой гиперболы имеет вид:

(3.27).

У равносторонней гиперболы, как нетрудно показать, угол между асимптотами прямой, и .

Для гиперболы, у которых оси совпадают и равны, но вещественная ось одной служит мнимой осью другой и наоборот, называются сопряженными; асимптоты таких гипербол также совпадают (поскольку совпадают их осевые прямоугольники), но гиперболы располагаются в смежных углах между асимптотами.

Нетрудно видеть, что если уравнением одной из сопряженных гипербол является уравнение (3.21):

,

то уравнение второй будет иметь вид:

,
или (3.28),

поскольку меняются ролями оси Ox и Oy и полуоси гипербол а и b.

Отметим, что расстояние с от центра до фокусов у обеих сопряженных гипербол одно и то же, определяемое формулой (3.24), но эксцентриситеты различные: , ; (если только обе гиперболы не являются равносторонними).

4.4. Парабола

Параболой называется геометрическое место точек плоскости, расстояния которых от заданных на той же плоскости точки (фокуса параболы) и прямой (директрисы параболы) равны между собой.

Пусть точка F – фокус; прямая KL – директриса параболы; М – произвольная точка параболы.

По определению параболы:

(3.29),

где В – основание перпендикуляра, опущенного из точки М на директрису KL.

Введем обозначение , где – основание перпендикуляра, опущенного из фокуса на директрису; величину , расстояние от фокуса до директрисы, называют параметром параболы.

Для вывода простейшего уравнения параболы оси координат расположим следующим образом: начало координат поместим в точку О – середину отрезка ; за ось примем прямую, которой принадлежит отрезок , причем за положительное ее направление примем направление от точки О к фокусу F; ось направим перпендикулярно оси , т. е. параллельно директрисе.

При таком выборе осей координаты фокуса будут 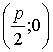, а уравнение директрисы .

Для точки , лежащей на параболе, имеем:

, ;

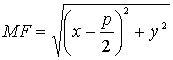подставляя эти значения в равенство (3.29), получаем:

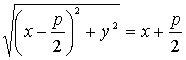(3.30).

Возведем обе части уравнения (3.30) в квадрат, одновременно раскрывая скобки:

.

Приводя подобные члены, получим простейшее (каноническое) уравнение параболы:

(3.31).

Построим параболу по этому уравнению.

Прежде всего отметим, что вся парабола расположена справа от оси ; в самом деле, в уравнении (3.31) левая часть неотрицательна (), в правой части ; следовательно, и второй множитель правой части неотрицателен: .

Поскольку в уравнение (3.31) текущая координата входит только во второй степени, заключаем, что ось является осью симметрии параболы. При и : парабола проходит через начало координат; эту точку называют вершиной параболы.

При возрастании одновременно возрастает и абсолютная величина , ибо .

При построении параболы полезно помнить, что ордината точки параболы, лежащей над ее фокусом, равна параметру параболы ; в самом деле, при из уравнения параболы (3.31) находим:

, откуда.

Таким образом, длина хорды параболы, проходящей через ее фокус перпендикулярно оси параболы, равна .

Если повернуть параболу относительно осей координат на угол против часовой стрелки, то в уравнении (3.31) координаты и поменяются местами и уравнение такой параболы запишется так:

(3.32)

Вершиной этой параболы по-прежнему является начало координат, но осью симметрии будет служить ось ; парабола лежит над осью .
Фокусом этой параболы будет точка 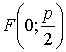; директрисой – прямая (рис. 3.8).

Нетрудно далее убедиться в том, что уравнения:

(3.33)

и

(3.34)

(в обоих случаях ) также определяют параболы, которые от парабол, определяемых уравнениями (3.31) и (3.32), отличаются только тем, что они направлены в сторону, противоположную направлению соответствующих координатных осей: первая – вдоль отрицательной оси , вторая – вдоль отрицательной оси .

Рекомендуем читателю самому найти координаты фокусов этих парабол и уравнения их директрис.

Уравнения парабол (3.31) и (3.33) можно записать в виде единого уравнения:

(3.31`),

а уравнения парабол (3.32) и (3.34) – в виде уравнения:

(3.32`),

если в уравнениях (3.31') и (3.32') рассматривать как коэффициент, принимающий и положительные, и отрицательные значения (параметр параболы будет равен ).

При парабола будет направлена в положительном направлении соответствующей оси координат, а при – в отрицательном.