В современных многоканальных системах с ЧД преобразователи частоты (индивидуальные и групповые) представляют собой нелинейные устройства, в которых в качестве нелинейных элементов используются полупроводниковые диоды или транзисторы. Поэтому преобразователи делятся на пассивные и активные.

Пассивные преобразователи частоты на диодах. В пассивных преобразователях частоты в качестве нелинейных элементов используются полупроводниковые диоды. Типичная амплитудная характеристика диода показана на рис. 1.8.

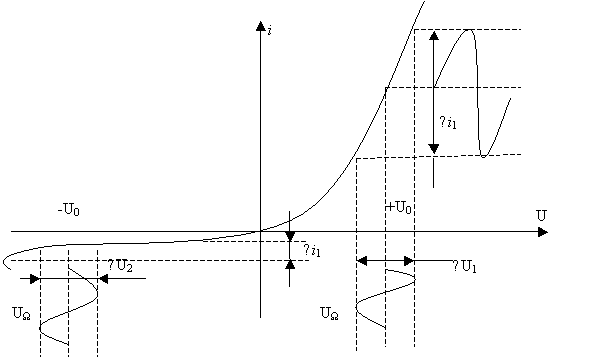
Рис. 1.8. Амплитудная характеристика диода

При весьма больших амплитудах напряжения, воздействующего на диод, его удобно рассматривать как параметрическое сопротивление, переходящее под влиянием приложенного управляющего напряжения из «открытого» состояния в «закрытое» и обратно. Если на диод подать большое постоянное отпирающее напряжение + U0 и наложить на него небольшое переменное напряжение с амплитудой 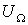<< 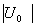, то сопротивление диода будет определяться постоянным смещением, т.е. он будет «открыт» (рис. 1.8.). В пределах небольшого используемого участка характеристику 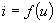можно считать линейной и определять сопротивление пропускания диода для переменного тока как 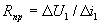. При подаче на диод постоянного напряжения противоположного знака –U0 («запирающего») нелинейный элемент будет «закрыт» и его сопротивление запирания можно определить как 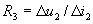. При идеализации диода полагают 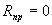и . 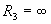У реальных диодов 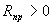и 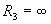, однако соотношение этих сопротивлений обычно весьма велико: .

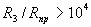Если включить нелинейный элемент в цепь переменного тока и подать на него управляющее переменное напряжение с большой амплитудой (рис. 1.9.а), то нелинейный элемент преобразуется в параметрическое активное сопротивление в цепи переменного тока и действие управляющего напряжения будет эквивалентно действию переключателя (рис. 1.9.б). Характеристику нелинейного элемента можно в этом случае аппроксимировать ломаной прямой линией (рис. 1.10)

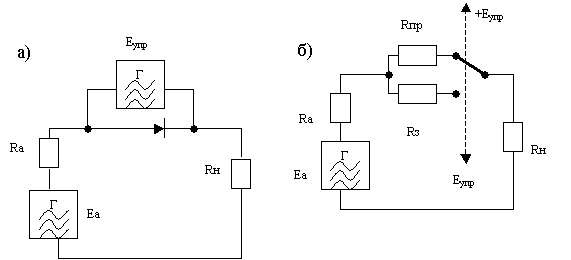
Рис.1.9. Схемы модулятора

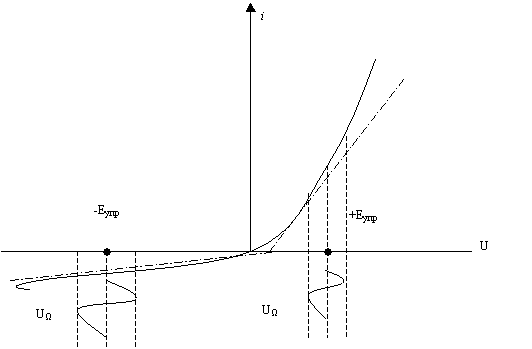
Рис. 1.10. характеристика нелинейного элемента

Если амплитуда несущего колебания 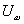во много раз превышает амплитуду модулирующего сигнала 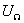, то напряжение несущей частоты является управляющим напряжением: сопротивление нелинейного элемента практически зависит только от знака напряжения несущей частоты и изменяется от 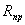при положительной полуволне несущего колебания до 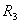при отрицательной полуволне. Строго говоря, это справедливо только при прямоугольной форме напряжения несущей, когда переход от амплитудного значения одного знака 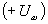к другому 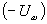происходит мгновенно. Однако при большой амплитуде напряжения несущей скорость его изменения при переходе через нуль достаточно велика и сделанное допущение не является слишком неточным.

При 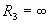можно считать, что ток в схеме преобразователя будет протекать только при положительных полуволнах несущей частоты, причем зависимость тока от напряжения на диоде будет линейной:

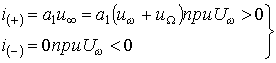(1.1)

где 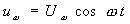- напряжение несущей частоты; 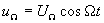- напряжение преобразуемого сигнала, который для упрощения может быть представлен в виде одночастотного гармонического колебания.

Амплитудная характеристика диода в таком режиме работы может быть представлена в виде линейно-ломаной характеристики. Такая аппроксимация характеристики диода будет тем точнее, чем меньше величина соотношения 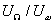. В многоканальных системах передачи такой режим работы называют режимом больших амплитуд (РБА). Форма огибающей тока в цепи однотактного преобразователя, работающего в режиме линейно-ломаной характеристики, соответствует форме преобразуемого сигнала.

Общее аналитическое выражение для тока в схеме преобразователя при любом знаке напряжения несущей частоты можно записать в виде [1].

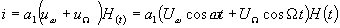(1.2.)

В этом выражении 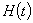- функция коммутации, или функция переключения, которая 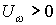при принимает значение +1, а при 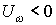- значение 0. График функции 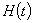показан на рис. 1.11.

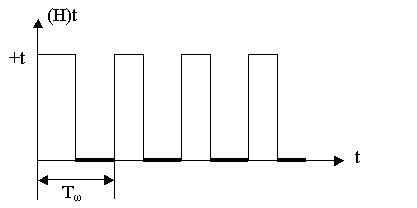
Рис.1.11. График функции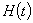

Разложение функции 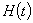в ряд Фурье имеет вид [1].

(1.3)

Подставив разложение (1.3.) в выражение для тока (1.2.) и произведя несложные тригонометрические преобразования, можно увидеть, что ток в схеме однотактного преобразователя, работающего в режиме линейно-ломаной характеристики, кроме колебаний полезных боковых частот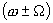 , будет содержать колебания с частотой сигнала , с частотой несущего колебания 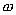и ее гармоник и колебания боковых частот около нечетных гармоник несущей частоты.

Предположим, что в однотактном преобразователе, содержащем идеальный нелинейный элемент, применены идеальные трансформаторы без потерь, согласующие сопротивление его выходной нагрузки 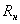с внутренним сопротивлением источника преобразуемого сигнала 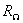, т.е. что 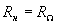. Предположим также, что внутреннее сопротивление источника несущего колебания пренебрежимо мало, т.е. . В этом случае однотактный преобразователь будет идеальным и эквивалентная схема его будет иметь вид, показанный на рис.1.12.

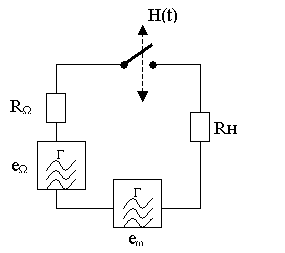
Рис. 1.12. Эквивалентная схема преобразователя

Ток в нагрузке идеального преобразователя будет определяться выражением 1.4.

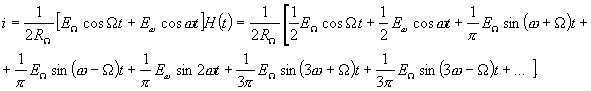(1.4.)

Одним из важнейших параметров пассивных преобразователей частоты является затухание, вносимое ими в тракт передачи. Рабочим затуханием преобразователя частоты называется величина 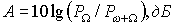(1.5.)

где - мощность, которую источник преобразуемого сигнала отдал бы в непосредственно подключенное к нему сопротивление нагрузки, равное его внутреннему сопротивлению; 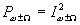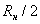- мощность полезной боковой частоты или , выделяющаяся на выходной нагрузке преобразователя; 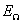- амплитуда ЭДС источника сигнала; 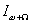-амплитуда тока боковой частоты, протекающего через сопротивление нагрузки. С учетом этих соотношений 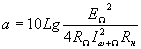(1.6.)

Для идеального однотактного преобразователя (см. рис. 1.12.) амплитуда тока полезной боковой частоты может быть определена из выражения (1.4.) :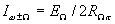 . Подставив это значение в выражение для рабочего затухания идеального однотактного преобразователя, получим при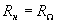

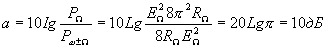(1.7.)

Однотактные преобразователи частоты не применяются в многоканальных системах, в которых при преобразовании частоты подавляется несущее колебание. В таких системах подавление несущей осуществляется в балансных или двойных балансных (кольцевых) схемах преобразователей.

Перейдем к рассмотрению балансных схем преобразователей и покажем, что, кроме подавления несущего колебания, эти схемы позволяют уменьшить число паразитных нелинейных продуктов в составе выходного тока по сравнению с однотактной схемой.

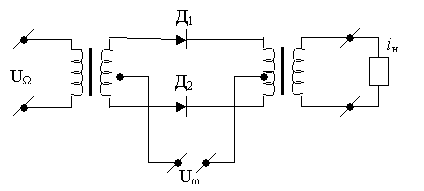
Балансная схема преобразователя частоты приведена на рис. 1.13

.

Рис. 1.13. Балансная схема преобразователя частоты

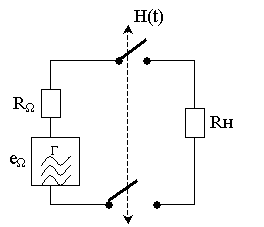
Рис. 1.14. Эквивалентная схема преобразователя частоты

Поскольку напряжение несущей частоты подается в средние точки трансформаторов на входе и выходе схемы, то можно сразу предположить, что в составе тока на выходе преобразователя ток несущей частоты будет отсутствовать. Если полагать, что сопротивления запирания обоих диодов, 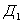и 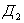, равны бесконечности, а сопротивления их пропускания – нулю, то схему балансного преобразователя можно заменить эквивалентной схемой (рис. 1.14.). В этой схеме 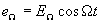и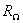 - электродвижущая сила источника преобразуемого сигнала, подаваемого на вход преобразователя, и его внутреннее сопротивление, пересчитанные во вторичную обмотку входного трансформатора; 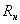- сопротивление нагрузки, пересчитанное в первичную обмотку выходного трансформатора. При одном полупериоде напряжения несущей частоты диоды находятся в режиме пропускания и, следовательно, цепь замыкается 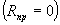и ток преобразуемой частоты проходит через сопротивление нагрузки; при другом полупериоде напряжения несущей частоты диоды переходят в режим запирания, следовательно, цепь разрывается и ток преобразуемой частоты через сопротивление нагрузки не проходит. Таким образом, преобразователь работает как ключ, замыкающий и размыкающий под действием напряжения несущей частоты цепь между входом преобразователя и сопротивлением нагрузки. Форма тока на выходе преобразователя приведена на рис. 1.15.

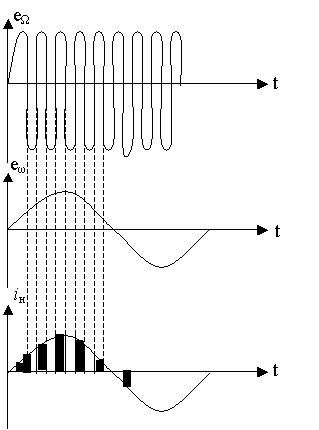
Рис. 1.15. Форма тока на выходе преобразователя

Из схемы рис. 1.13. видно, что ток на выходе преобразователя 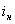будет определяться разностью токов, протекающих через оба диода, т.е. 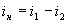. Для той же схемы можно написать выражения для напряжений, воздействующих на диоды: если в данный момент на первый диод 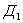воздействует напряжение 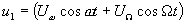, то на второй диод 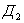воздействует напряжение 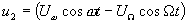,поскольку напряжение модулирующего сигнала подается на диоды в противоположных фазах. В соответствии с выражением (1.2.)

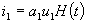и

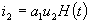
Следовательно, разностный ток определиться как

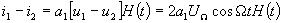
Предположим, что в схеме балансного преобразователя с идеальными нелинейными элементами используются идеальные трансформаторы без потерь, согласующие сопротивление нагрузки с сопротивлением источника преобразуемого сигнала так, что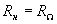 (также, как и при идеализации однотактного преобразователя). В этом случае для тока в нагрузке идеального балансного преобразователя (см. рис. 1.2.7.) получим выражение

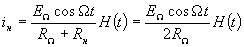
Подставив значение из (1.2.) и произведя тригонометрические преобразования, получим 1.8.

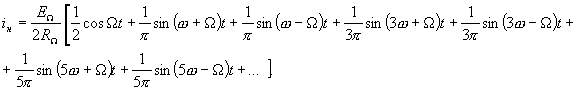(1.8.)

Из выражения (1.8.) видно, что на выходе балансного преобразователя имеется исходный преобразуемый сигнал с частотой 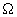, колебания полезных боковых частот 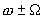, а также колебания боковых частот около нечетных гармоник несущей частоты: 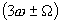, 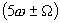и.т.д. Ток несущей частоты и его гармоники на выходе балансного преобразователя отсутствуют, что подтверждает сделанное ранее предположение.

Определим рабочее затухание идеального балансного преобразователя. Сравнивая выражения для амплитуды тока полезной боковой частоты в выражениях (1.4.) и (1.8.), можно увидеть, что при одинаковых значениях ЭДС преобразуемого сигнала и его внутреннего сопротивления эти амплитуды в однотактном и балансном преобразователях равны друг другу. Следовательно, и рабочее затухание идеального балансного преобразователя равно рабочему затуханию идеального однотактного, т.е. затухание балансного преобразователя равно

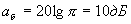(1.9.)

Кольцевая или двойная балансная схема преобразователя (рис. 1.16.)

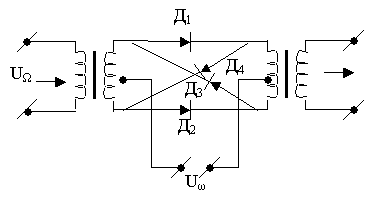
Рис. 1.16. Кольцевая или двойная балансная схема

При одинаковых характеристиках всех диодов падения напряжений модулирующего сигнала на диодах будут равны друг другу. И напряжение модулирующего сигнала в нагрузке будет равно нулю.

Если принять, как раньше, сопротивления пропускания диодов равными нулю, а сопротивления запирания равными бесконечности, то эквивалентную схему кольцевого преобразователя можно представить, как это показано на рис. 1.17.

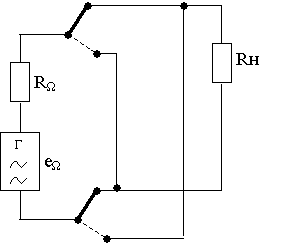
Рис. 1.17. Эквивалентная схема кольцевого преобразователя

Если принять, как и раньше, сопротивления пропускания диодов равными нулю, а сопротивления запирания равными бесконечности, то эквивалентную схему кольцевого преобразователя можно представить, как это показано на рис. 1.17. В этой схеме ток в нагрузке преобразователя протекает в течение обоих полупериодов напряжения несущей частоты, но направление этого тока во время положительного и отрицательного полупериодов различно. Таким образом, преобразователь работает как переключатель направления тока. Форма тока на выходе преобразователя показана на рис. 1.18.

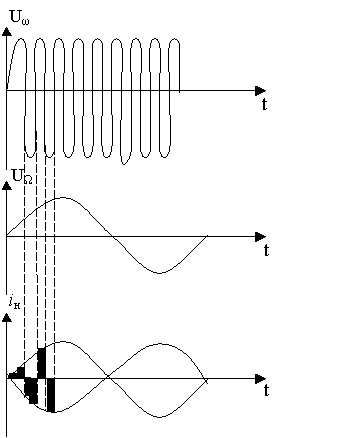
Рис. 1.18. Форма тока на выходе преобразователя

Из схемы рис. 1.16. видно, что ток в нагрузке преобразователя будет определяться алгебраической суммой токов, протекающих через все диоды, т.е. 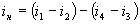. Для этой же схемы можно написать выражения для напряжений, воздействующих на диоды: если в данный момент на первый диод воздействует напряжение 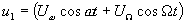, а на второй диод - напряжение 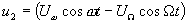(как в балансной схеме), то, поскольку на диоды напряжение несущей частоты подается в противофазе по сравнению с двумя первыми, на третий диод будет воздействовать напряжение 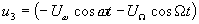, а на четвертый диод - напряжение 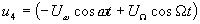. Изменение знака напряжения несущей частоты на диодах 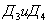по сравнению с диодами 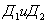соответствует сдвигу переключающей функции H(t) на полпериода несущей частоты Т/2. Ток на выходе преобразователя будет равен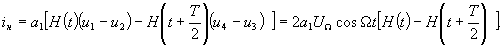

Разложение функции 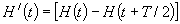(рис.1.2.12) в ряд Фурье будет иметь вид [1].

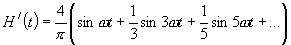(1.10)

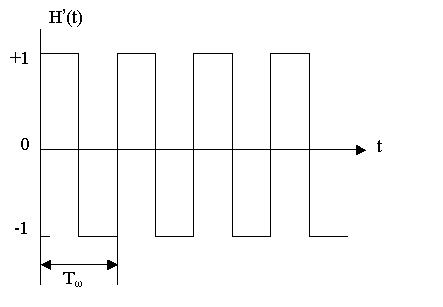
Рис.1.19. Ток на выходе кольцевого преобразователя

Учитывая сопротивления источника и нагрузок так же, как в случае балансной схемы, получим выражение для тока в нагрузке кольцевого преобразователя:

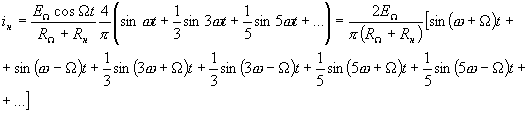(1.11.)

Из этого выражения видно, что ток на выходе кольцевого преобразователя содержит только составляющие полезных боковых частот и боковых частот около нечетных гармоник несущей частоты. На выходе преобразователя отсутствует ток с частотой исходного модулирующего сигнала, что является одним из достоинств кольцевой схемы. Общее выражение для частот составляющих выходного тока может быть представлено в ви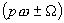де , где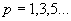

При неидеальной балансировке балансной и кольцевой схем преобразователей в спектре на их выходе появляются дополнительные паразитные продукты преобразования; так, на выходе кольцевой схемы может появиться ток с частотой модулирующего сигнала. Такое же влияние оказывает и то обстоятельство, что реальный режим работы нелинейных элементов отличается от идеального режима, в котором их характеристики аппроксимируются ломаной прямой.

Основными методами уменьшения числа и амплитуд паразитных нелинейных продуктов на выходе преобразователя являются: применение кольцевой схемы, вместо простой балансной, так как спектр на выходе кольцевой схемы всегда содержит меньшее число паразитных продуктов; особо тщательная балансировка схемы, что может контролироваться по уровню несущего тока, просачивающегося на ее выход; как можно большее приближение к идеализированному режиму «линейно-ломаной» характеристики, что достигается уменьшением соотношения .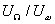

Затухание идеального кольцевого преобразователя можно определить, полагая также трансформаторы идеальными и сопротивления .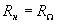

Амплитуда тока полезной боковой частоты 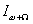или 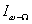определяется из выражения (1.11.):

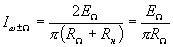
Подставив это значение в выражение (1.6), получим величину затухания кольцевого преобразователя:

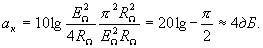(1.12)

Из сравнения выражений (1.9.) и (1.12) видно, что затухание кольцевого преобразователя меньше, чем затухание балансного преобразователя, на 6 дБ при тех же условиях. Это объясняется тем, что в кольцевой схеме источник преобразуемого сигнала отдает мощность в нагрузку в течение обоих полупериодов напряжений несущей частоты, а во всех балансных схемах – только в течение одного из полупериодов.

Все выводы при определении амплитуд составляющих тока в нагрузке преобразователей, а следовательно, и при определении затуханий преобразователей производилась для идеализированных нелинейных элементов, т.е. диодов с нулевым сопротивлением пропускания и бесконечно большим сопротивлением запирания. При учете реальных значений этих сопротивлений значения токов полезных боковых частот будут меньше, а затухание преобразователей больше. Однако во всех случаях затухание кольцевой схемы будет меньше затухания балансных схем.

Если учесть, что сопротивление диодов имеет и реактивную составляющую, получающуюся за счет межэлектродной емкости, шунтирующей их сопротивление и, следовательно, уменьшающей сопротивление запирания, то увеличение затухания схем преобразователей по отношению к рассмотренному идеализированному случаю будет еще больше. Кроме того, в реальных преобразователях необходимо учитывать потери, вносимые обмотками трансформаторов, которые составляют в каждом из них 0,45-0,6 дБ.

Для обеспечения заданных входных и выходных сопротивлений пассивных преобразователей на их входах и выходах обычно включаются удлинители. С учетом затуханий этих удлинителей величины затуханий преобразователей составляют 20-30 дБ для балансных и 15-25 дБ для кольцевых схем.

Применение активных преобразователей на транзисторах позволило одновременно с преобразованием сигнала осуществить его усиление.

Активные преобразователи частоты на транзисторах. Возможность использования транзисторов для целей преобразования частоты обусловливается нелинейностью их вольтамперных характеристик. На рис. 1.20а приведена типичная входная вольтамперная характеристика транзистора, включенного по схеме с общим эмиттером. Так как эта характеристика аналогична вольтамперной характеристике диода (см. рис.1.2.), ее также можно заменить линейно-ломаной характеристикой (показана пунктиром на рис. 1.20а). Таким образом, можно написать, что

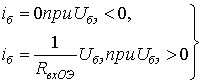(1.13)

где 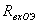- входное сопротивление транзисторного каскада с ОЭ. На рис.1.20б показана схема транзисторного преобразователя при включении источника сигнала и источника несущего колебания во входной цепи.

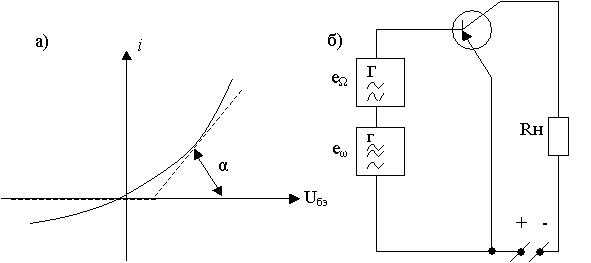
Рис.1.20

Для определения спектрального состава входного тока транзистора будем полагать, что напряжение несущей частоты значительно превышает напряжение преобразуемого сигнала, и полярность суммарного напряжения 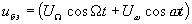определяется полярностью колебания несущей частоты. В этом случае по аналогии с диодным преобразователем для определения спектра входного тока можно ввести функцию коммутации H(t), период которой совпадает с периодом несущей частоты (см. рис. 1.20). Входной ток будет равен

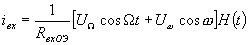(1.14)

Выражение (1.14) аналогично выражению (1.2.) для тока в цепи однотактного пассивного преобразователя. Подставляя вместо функции H(t) ее разложение в ряд (1.3.), получим спектр входного тока транзистора такой же, как спектр тока в цепи однотактного преобразователя. Кроме полезных составляющих с частотами 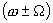, этот спектр будет содержать большое число паразитных составляющих: колебания с частотой сигнала 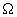, с частотой несущего колебания 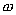и ее гармоник и колебания боковых частот около нечетных гармоник несущей. Таким образом, в первом приближении входную цепь транзисторного преобразователя можно рассматривать как однотактный пассивный преобразователь.

Для упрощения дальнейших рассуждений предположим, что в идеальном случае 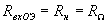,,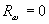 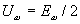и . Тогда

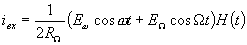
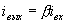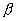Полагая преобразователь безынерционным, можно считать, что спектр тока на его входе и выходе будет одинаков. Для схемы с ОЭ , где - усиление по току, которое можно считать не зависящим от частоты. Поэтому ток на выходе преобразователя будет равен

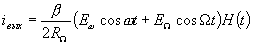(1.15)

Усиление транзисторного преобразователя можно определить как 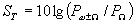, дБ,

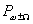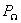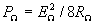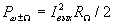где - мощность одной из боковых частот в нагрузке на выходе преобразователя; - мощность, отдаваемая источником преобразуемого сигнала в согласованную с ним нагрузку; и , где 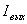- амплитуда тока полезной боковой частоты, протекающего через выходную нагрузку преобразователя.

Величину 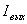можно определить, подставив в выражение (1.15) значение функции H(t) из (1.2.). Произведя соответствующие тригонометрические преобразования, получим 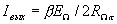. Усиление транзисторного преобразователя будет, следовательно, равно

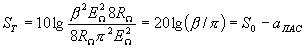(1.16)

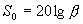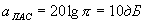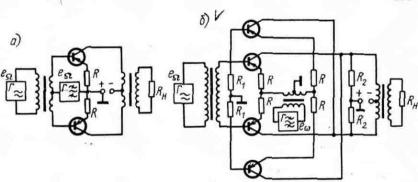
где - усиление каскада с ОЭ; - затухание идеального однотактного пассивного преобразователя (1.13). Таким образом, усиление транзисторного каскада 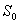должно компенсировать затухание пассивного однотактного преобразователя, которым является его входная цепь.

Однотактные транзисторные преобразователи имеют те же недостатки, что и однотактные диодные преобразователи: на их выходе получается большое количество паразитных нелинейных продуктов и они не подавляют несущее колебание и его гармоники. Поэтому на практике нашли применение более сложные схемы транзисторных преобразователей – балансные (рис. 1.21а) и кольцевые (рис. 1.21б).

а) Балансная схема преобразователя

б) Кольцевая схема преобразователя

Рис. 1.21

В любой из схем транзисторы могут быть включены по схеме с общим эмиттером или с общей базой, а источники сигнала и несущей – оба в цепь базы, в цепь эмиттера или смешанно – один в цепь базы, другой в цепь эмиттера.

Анализ различных вариантов схем преобразователей с транзисторными элементами достаточно сложен и трудоемок и поэтому, здесь его приводить не будем

Можно показать, что усиление балансного транзисторного преобразователя равно усилению однотактного преобразователя: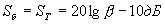 , а усиление кольцевого преобразователя равно 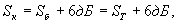т.е. соотношения между ними остаются такими же, как для пассивных преобразователей.

В активных преобразователях для стабилизации работы каскадов по постоянному и переменному токам и для уменьшения нелинейных искажений, как правило, применяется отрицательная обратная связь (ООС). Глубина ООС составляет обычно около 20 дБ. Таким образом, если транзисторный каскад в режиме класса А без ООС может давать усиление 25-35 дБ, то усиление этого каскада с ООС будет составлять всего 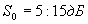. Результирующее усиление транзисторного преобразователя будет в этом случае равно для балансной схемы: 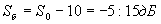и для кольцевой схемы: .

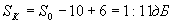Таким образом, транзисторные преобразователи обычно дают небольшое усиление, близкое к нулю. Однако в сравнении с большим затуханием, вносимым пассивными преобразователями, выигрыш в уровне сигнала получается значительным. Кроме того, при использовании глубокой ООС характеристики транзисторных преобразователей получаются весьма стабильными.

В некоторых случаях транзисторные преобразователи используются в ключевом режиме, не давая усиления. Представляет, в частности интерес схема пассивного преобразователя на одном полевом МОП-транзисторе, показанная на рис.1.22.

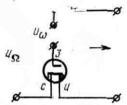
Рис.1.22. Пассивный преобразователь на МОП-транзисторе

Несущая частота с большой амплитудой подается в цепь затвора и управляет сопротивлением сток – исток, работающим как ключ в цепи передачи сигнала. Спектр на выходе такого преобразователя на одном транзисторе получается такой же, как и на выходе балансного преобразователя, т.е. он содержит теоретически только составляющие с частотой сигнала, полезные боковые частоты и боковые частоты около нечетных гармоник несущей. Практически из-за паразитной емкости полевого транзистора на выход преобразователя может просачиваться несущий ток с пониженным уровнем.