При наблюдении за течением случайного процесса мы можем определить лишь текущий спектр данной реализации x(t), т. е.
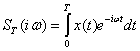 (2.80)
(2.80)
Эта функция является случайной. Поэтому удобно ввести понятие энергетического спектра, которое приводит к неслучайной функции частоты.
Энергетический спектр стационарного случайного процесса определяется как спектр его функции корреляции.
![]() (2.81)
(2.81)
Обратное преобразование Фурье дает
![]() (2.82)
(2.82)
Так как B(τ) и G(ω) — четные, функции своих аргументов, то ф-лы (2.81) и (2.82) можно записать в другом виде:
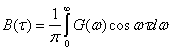 (2.83)
(2.83)
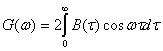 (2.84)
(2.84)
Физический смысл функции G(ω) легко выяснить на основании (2.82), если в последнем положить τ=0. При этом мы получаем
![]() (2.85)
(2.85)
где Р — полная мощность процесса.
Формула (2.85) показывает, что функция G(ω) выражает спектральную плотность мощности процесса. Мощность в полосе ![]() — можно определить интегрированием G(ω) в пределах от
— можно определить интегрированием G(ω) в пределах от ![]() до
до ![]() , т. е.
, т. е.
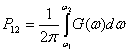
Энергетический спектр можно выразить и через текущий спектр реализации i(2.80). Согласно равенству Парсеваля энергия процесса x(t), выделяющаяся за время Т, равна:
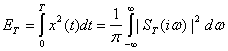 (2.86)
(2.86)
Средняя мощность процесса определится как предел ЕТ/Т при ![]() , т. е.
, т. е.
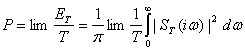 (2.87)
(2.87)
Сопоставляя (2.85) и (2.87), находим
![]() (2.88)
(2.88)
Это соотношение устанавливает связь между энергетическим спектром процесса и текущим спектром его реализации.
Энергетический спектр характеризует поведение реализаций процесса в среднем. Так, если спектр G(ω) сосредоточен в области низких частот, то процесс этот — медленно изменяющийся по сравнению с тем процессом, у которого спектр сосредоточен в области. более высоких частот. Для узкополосного процесса G(ω) заметно отличается от нуля только в полосе Δω вокруг средней частоты ![]() ) причем Δω<<
) причем Δω<<![]() . Такой процесс напоминает синусоиду с медленно меняющимися амплитудой и фазой.
. Такой процесс напоминает синусоиду с медленно меняющимися амплитудой и фазой.
Поскольку энергетический спектр и функция корреляции связаны между собой парой преобразований Фурье, то к ним можно применить известные теоремы спектрального анализа. Некоторые соотношения из этих теорем приведены в табл. 2.1. Здесь предполагается, что х=0, a ![]() и
и![]() — независимы.
— независимы.
Случайный процесс, у которого G(ω)=![]() — постоянная величина, называется белым шумом.
— постоянная величина, называется белым шумом.
Таблица 2.1

Корреляционная функция белого шума согласно (2.82) равна:
![]() (2.89)
(2.89)
Для случайных процессов имеет место связь общего характера между шириной спектра Δf, и интервалом корреляции Δτ:
![]() (2.90)
(2.90)
где μ — постоянная порядка единицы. Интервал корреляции вычисляется на основании выражения (2.24). Ширина энергетического спектра определяется аналогичным соотношением
![]() (2.91)
(2.91)
Пусть, например, задан процесс, функция корреляции которого определяется выражением ![]() . Энергетический спектр такого процесса согласно (2.84)
. Энергетический спектр такого процесса согласно (2.84)
![]()
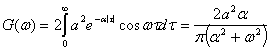
Далее, ![]() , а согласно (2.24)
, а согласно (2.24)![]() . Затем
. Затем ![]() отсюда
отсюда ![]() .
.

