1.1. Классификация и состав систем управления

1.2. Способы управления технологическими объектами

1.3. Методы выбора периода квантования

1.4. Типичные алгоритмы непосредственно цифрового управления

1.1. Классификация и состав систем управления

В общем случае любая система (техническая, биологическая, экономическая, социальная и т.д.) представляет собой множество взаимосвязанных элементов. В автоматике под системой подразумевают совокупность объектов управления и управляющего устройства, которые взаимодействуют между собой. В сфере промышленного производства сегодня практический интерес имеют системы управления трех категорий: локальные, централизованные и автоматизированные системы управления технологическими процессами. К первой категории систем автоматики относятся локальные (местные) средства контроля, регулирования и управления. Эти системы находят широкое применение на хорошо изученных «простых» объектах управления с числом измерительных величин, не превышающих десятка, например, для котельных установок малой мощности, кондиционеров, холодильных агрегатов и других объектов. Они эффективны при автоматизации технологически независимых объектов с компактным расположением основного оборудования и несложными целями управления (стабилизация, слежение, программное и логическое управление, контроль и измерение) при хорошо отработанной технологии и стационарных условиях эксплуатации.

Появление централизованных систем автоматики связано с ростом количества контролируемых параметров, с территориальным размещением объектов управления. Они разрешают реализовать новые функции по вычислению комплексных показателей эффективности работы отдельных агрегатов и технико-экономических показателей всего технологического процесса, вычислению на этой основе оптимальных управляющих действий и реализации этих действий или в виде вставок локальных регуляторов, или в виде непосредственного действия на исполнительное устройство.

Более высокие требования к качеству управления за счет повышения количества контролируемых параметров, осуществления более точного и комплексного контроля сырья и промежуточных продуктов, оптимального управления объектами на основе их математической модели создали предпосылки к использованию систем третьей категории - АСУТП. В этих системах объединяются решения задач контроля и регулирования технологических процессов, выбора оптимальных режимов и алгоритмов управления.

Несмотря на численное разнообразие систем управления, общим для них является наличие элементов: объекта управления, устройства управления, устройства связи с объектом, получение и использование информации (датчики).

Типичная структура системы управления приведена на рис. 1.1. Показанные на ней аппаратные средства, которые составляют систему, можно разделить на следующие основные части:

• устройство управления (УУ);
• устройство связи с объектом (УСО);
• периферийные устройства (датчики (Д));
• исполнительные устройства, органы (ИО).

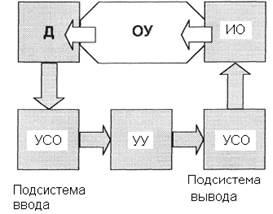
Рисунок 1.1. Структурная схема системы управления

Устройства, которые обеспечивают возможность подключения управляющего устройства к объекту управления (ОУ), выделяют в специальный класс периферийных устройств - устройства связи с объектом (УСО), которые включают в себя подсистемы аналогового и цифрового ввода, подсистемы аналогового и цифрового вывода.

Подсистема аналогового ввода преобразовывает аналоговые физические величины в форму, пригодную для использования в устройстве управления. С помощью соответствующих датчиков аналоговые величины разной физической природы превращаются в большинстве случаев в постоянный ток или напряжение.

Основные функции оборудования подсистемы:

• нормализация и усиление сигнала, фильтрация, ослабление сигнала, смещение уровня, преобразование и др.;
• коммутация сигналов;
• аналого-цифровое преобразование.

Разнообразные требования по стоимости и техническим характеристикам дают возможность вариации структуры подсистемы аналогового ввода на основе выбора метода обработки аналоговых сигналов.

На рис. 1.2 приведена структура, которая реализует принцип параллельной обработки аналоговых сигналов, поступающих от датчиков. Данная структура даёт возможность обеспечить максимальную производительность аппаратуры всех каналов подсистемы вследствие независимости обработки каждого сигнала и высокое качество преобразования сигналов вследствие возможности подсистемы обеспечить нужный уровень сигнала на входе аналого-цифрового преобразователя (АЦП) в каждом канале. Такой вариант построения подсистем имеет большое будущее, но на современном этапе развития микросхемотехники при его реализации имеет место высокая стоимость системы из-за сравнительно высокой стоимости интегральных схем АЦП.

Другие варианты (рис.1.3) построения структуры подсистем аналогового ввода базируются на принципе последовательной обработки аналоговых сигналов, применения мультиплексирования, а также аналоговых схем выборки-хранения для фиксации аналоговых сигналов на входе АЦП.

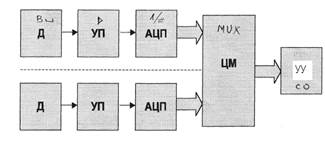
Рисунок 1.2. Структура подсистемы аналогового ввода с параллельными цифровыми вводами сигналов

Это дает возможность использовать только один АЦП независимо от количества аналоговых входов.

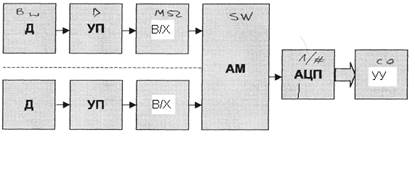
Рисунок 1.3. Структура подсистемы с параллельным аналоговым вводом и последовательным цифровым выводом сигналов

Хорошее качество преобразования обеспечено теми же функциональными блоками, которые входят в состав структуры (рис. 1.2). Производительность данной структуры находится в прямой зависимости от АЦП и ограничена его динамическими параметрами, поэтому в таких подсистемах необходимо использовать АЦП, имеющие высокое быстродействие. Использование дополнительных элементов для обработки аналоговых сигналов мультиплексоров, схем выборки-хранения ухудшает характеристики точности подсистемы в целом. Практически идентичными техническими характеристиками по сравнению со структурой (рис. 1.3), обладает подсистема (рис. 1.4).

Аппаратные затраты для реализации подсистемы на основе структуры (рис. 1.3) более высокие по сравнению с затратами для построения структуры с одной схемой выборки-хранения (рис.1.4). Эту конфигурацию структуры наиболее рационально использовать в однократных событиях.

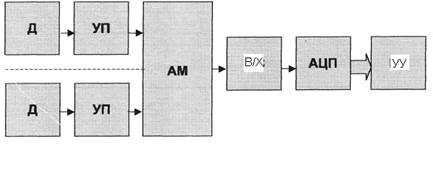
Рисунок 1.4. Структура подсистемы аналогового ввода с последовательным выводом сигналов

Простейшей, но обеспечивающей относительно низкое качество преобразования, является подсистема, построенная по структуре, приведенной на рис. 1.5.

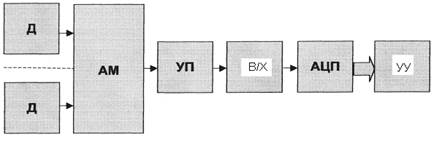
Рисунок 1.5. Рациональная структура подсистем аналогового ввода и аналогового вывода сигналов

Эта конфигурация структуры рациональная при условии существования сигналов высокого уровня, которые поступают с датчиков, и идентичности этих сигналов. В этом случае имеется возможность обеспечения необходимого качества преобразования при сохранении преимущества простоты реализации.

Из анализа возможных вариантов построения структур вытекает, что любой вариант реализуется на основе функциональных устройств: датчиков, устройств согласования, АЦП, цифровых мультиплексоров, аналоговых мультиплексоров, устройств выборки-хранения.

Подсистема аналогового вывода во многом напоминает подсистему аналогового ввода и используется для представления на объект контроля сигналов в виде напряжения или тока, которые изменяются во времени по заданному закону. При преобразовании цифровых данных в аналоговый сигнал с помощью ЦАП выделяют две конфигурации подсистем аналогового вывода:

• с цифро-аналоговым преобразователем в каждом канале;
• с одним ЦАП, который работает в режиме распределения времени.

Первая конфигурация применяется там, где есть потребность в высокой скорости и точности. Вторая конфигурация менее ценная, так как применяется только один ЦАП. В этом случае подсистема должна
вмещать ряд исходных схем аналоговой памяти.

Подсистема цифрового ввода-вывода. Для систем автоматики характерны не только аналоговые входные и выходные величины, но и цифровые. Они могут быть представлены двумя состояниями, например, "включено" или "выключено", "в пределах" или "за пределами", "низкий уровень" или "высокий уровень". Кроме цифровых параметров, которые характеризуют состояние объекта, существуют выходные цифровые параметры, которые задают желательное состояние объекта. Например, при контроле объекта часто возникает необходимость включения или отключение блоков и модулей, которые его составляют.

В этих подсистемах в качестве преобразующих схем входных сигналов используют резистивные делители напряжения, диодные ограничители, компараторы, триггеры Шмидта, согласователи уровней.

Основная функция подсистемы цифрового вывода – функция ключа. Выбор типа ключа определяется значением мощности, которая коммутируется, а также величиной скорости переключения. Электромеханические реле используют в основном для управления средней и большой мощностью при низких скоростях переключения. Они обеспечивают полную гальваническую развязку цепи.

Более надежными элементами являются полупроводниковые ключи (биполярные и полевые транзисторы).

Для коммутации цепей переменного тока средней и большой мощности часто используются кремниевые выпрямители, которыми можно управлять. Практически совершенными переключающими характеристиками обладают полевые транзисторы. Для гальванической развязки полупроводниковых ключей используют оптоэлектронные пары.

1.2. Способы управления технологическими объектами

Любое управление строится на основе информации о состоянии объекта управления и сопоставления информации с целью управления и формирования по результатам этого сопоставления соответствующего управляющего воздействия. Все эти задачи решаются управляющим устройством, в качестве которого в системах управления все чаще используются средства вычислительной техники (СВТ). К ним относятся микропроцессоры, микроконтроллеры и персональные компьютеры.

Использование средств вычислительной техники в управлении технологическими процессами дает возможность:

• компенсировать программным путем недостатки датчиков (нелинейность характеристики, наличие зоны нечувствительности и сдвига нуля);
• вычислять значение выходных управляющих параметров технологического процесса по математической модели при отсутствии необходимых датчиков;
• рассчитывать в автоматическом режиме оптимальную структуру и параметры отладки цифровых регуляторов при изменении динамических параметров объекта управления;
• реализовывать совершенные алгоритмы управления, которые могут перестраиваться программным путем при изменении динамики объекта, технологии производства, ситуации в ходе технологического процесса;
• учитывать при управлении не только текущее состояние объекта, но и его предысторию.

Управление технологическими объектами с использованием СВТ можно осуществлять тремя способами:

• управление в режиме советника;
• супервизорное управление;
• непосредственное цифровое управление.

На рис. 1.6 приведена схема системы управления с использованием СВТ в режиме советника.

Рисунок 1.6. Режим советника

Информация о состоянии объекта управления снимается с датчиков, обрабатывается и в удобной форме предоставляется оператору (О). Характерная особенность такого режима - формирование влияния на объект управления оператором через исполнительные органы системы.

В режиме супервизорного управления выполняется автоматическая коррекция установок локальных регуляторов с помощью постоянного подключения выводов управляющего устройства через устройство связи с объектом до установок локальных аналоговых регуляторов. В этом случае СВТ работают в замкнутом контуре второго уровня управления и используются для решения задач статической оптимизации технологических объектов управления.

При непосредственном цифровом управлении предполагается выполнение следующих операций:

• определение в СВТ ошибки несогласования между задающим воздействием и полученным значением;
• опрос датчиков в дискретные моменты времени, превращение информации в цифровой код и введение в запоминающее устройство средств вычислительной техники;
• формирование управляющего воздействия с помощью алгоритма управления;
• преобразование цифрового сигнала в аналоговый управляющий и выдача его на исполнительный механизм (орган).

Схема системы управления в режиме непосредственного цифрового управления (НЦУ) представлена на рис. 1.7.

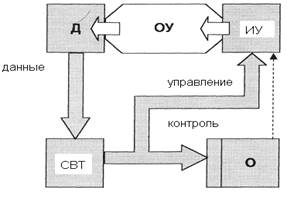
Рисунок 1.7. Режим НЦУ

Информационная связь между системой управления и ОУ осуществляется с помощью датчиков и исполнительных органов. Отличительной особенностью работы СВТ в режиме непосредственного цифрового управления является наличие предельно допустимой задержки между моментами введения информации, обработки и выдачи управляющего воздействия.

При реализации контуров НЦУ применяются синхронный и асинхронный принципы связи управляющих СВТ с объектом. При синхронном обмене процесс управления разбивается тактовыми импульсами на такты, за это время осуществляются снятие данных с ОУ, их обработка и выдача управляющего воздействия. При асинхронном обмене в СВТ поступают импульсы от датчиков прерывания, при этом на некоторое время прерывается выполнение основной программы, запоминается промежуточная информация и выполняется подпрограмма по сигналу прерывания. После этого осуществляется возвращение к прерванной программе.

Таким образом, необходимо решать такие задачи:

• Анализ ОУ и разработка математической модели.
• Определение структуры системы управления.
• Проектирование алгоритма управления.
• Выбор оптимального периода опроса датчиков и выдачи управляющего воздействия.
• Выбор типа СВТ и разработка системы для реализации заданных алгоритмов, включая выполнение требований к устройствам связи с объектом.
• Реализация программного обеспечения.

Структура типичного контура НЦУ, который реализуется на базе СВТ, представлена на рис. 1.8. СВТ выполняют функции задающего, сравнивающего и управляющего устройств.

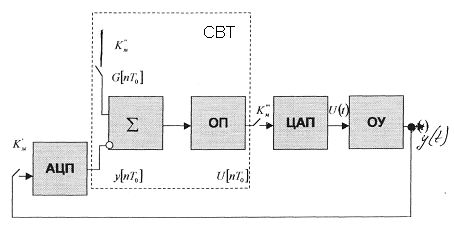
Рисунок 1.8. Структурная схема контура НЦУ

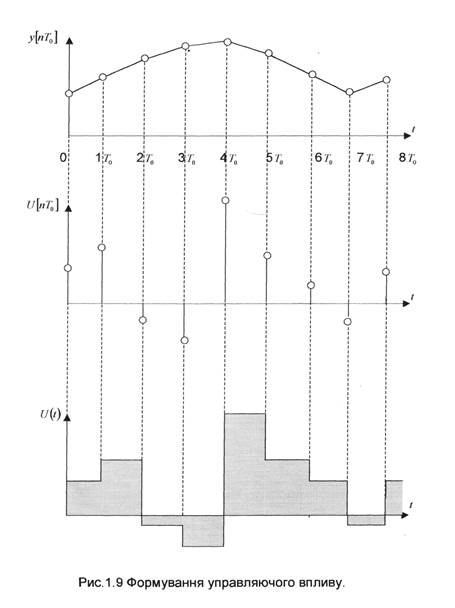
Рисунок 1.9. Формирование управляющего воздействия

Исходная регулируемая величина y(t) в дискретные моменты времени поступает через коммутатор на аналого-цифровой преобразователь. С помощью коммутатора аналоговых сигналов осуществляется квантование непрерывного сигнала с периодом квантования Т₀, в результате чего координата y(t) превращается в решетчатую функцию y[nТ₀]. На каждом периоде квантования в сравнивающем устройстве определяется ошибка регулирования:

e [n₀]=G[n₀]-y[n₀], (1.1)

где G[n₀] - влияние, которое задается цифровым регулятором.

Вычислительное устройство (ВУ) на основании алгоритма НЦУ формирует управляющее воздействие u[n₀] в виде цифрового кода, который через коммутатор в каждый период квантования подключается ко входу цифро-аналогового преобразователя. С помощью ЦАП осуществляется преобразование последовательности значений u[n₀] в непрерывный сигнал u(t), который остается постоянным на протяжении следующего периода квантования nT₀ до появления следующего члена последовательности u[(n+1)T₀] ( рис. 1.9).

СВТ в мультипрограммном режиме обслуживают поочередно каждый контур НЦУ, определяют управляющее воздействие U_i(n₀), где i = 1,2,…, Р - номер цифрового регулятора. С помощью регистров цифро-аналоговых преобразователей выполняется запоминание управляющего воздействия в каждом контуре НЦУ за весь период квантования T_0i. Вычислительное устройство, с помощью которого реализуется цифровой регулятор, работает в реальном масштабе времени. Коммутатор выполняет функции импульсного модулятора, прохождение сигнала через который связано с потерей части информации, которая находится в нем, так как в промежутках между импульсами U(n₀) характер изменения управляющего воздействия U остается неизвестным.

Задача оптимального выбора периода квантования относится к одной из основных проблем оптимального расходования машинного времени, затраченного на каждый контур НЦУ. При уменьшении Т₀ увеличиваются точность регулирования и загрузка СВТ, но неэкономно тратится машинное время. При большом Т₀ ухудшается качество регулирования системы, поэтому возникает проблема поиска компромиссного решения, которое удовлетворяет необходимым требованиям.

Таким образом, выбор Т₀ сводится к нахождению зависимости точности управления от величины периода квантования управляющего воздействия u[n₀] и управляющей переменной y[n₀].

1.3. Методы выбора периода квантования

В системах НЦУ ввод сигналов от датчиков и выдача управляющих воздействий на объект происходят в дискретные моменты времени, в паузах между которыми объект остается нерегулируемым и осуществляет принудительные движения под влиянием управляющих воздействий U[n₀] и возмущений. Выбор Т₀ в зависимости от спектра непрерывной функции выполняется на основе теоремы Котельникова, согласно которой функция y(t), не содержащая гармонических составляющих выше частоты , полностью определяется своими значениями в моменты времени nT_o, отстоящими друг от другого на периоды

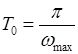(1.2),

т.е. частота квантования должна быть выбрана согласно

. (1.3)

В этом случае дискретная функция y[n₀] точно отобразит непрерывную y(t) и потерь информации при квантовании не будет. Для оценки периода квантования существует критерий Джури.

Критерий Джури расчёта периода квантования основан на оценке максимальной частоты в спектре исходного сигнала и определяется по амплитудно-частотной характеристике замкнутого контура НЦУ:

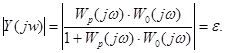(1.4)

Из формулы (1.4) определяется _о, причем величина погрешности минимальна, если рассогласование выбирается в пределах . Период квантования T₀ определяется согласно (1.2), и принимается ближайшее меньшее значение.

Рассмотрим пример.

Частотная передаточная функция объекта регулирования имеет вид

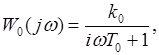
где k = 0.7038; Т₀ = 30с.

Определить оптимальный период квантования в системе с ПИ-регулятором НЦУ, параметры которого равны:

К_р = 1.22; Т_р = 30с.

При этом необходимо обеспечить точность регулирования в постоянном режиме = 0,03.

Согласно рассмотренному критерию Джури период квантования определяется таким образом. Определяем частотную передаточную функцию замкнутой системы

,

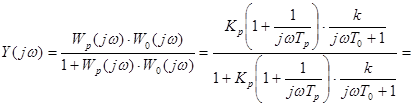
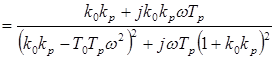откуда АЧХ определяется как

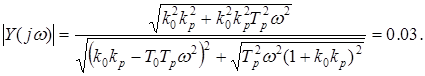
Решая полученное уравнение, находим частоту Оптимальный период квантования согласно критерию Джури равен

.

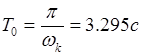Принимаем Т₀ = 3с.

Согласно критерию обеспечения необходимой точности управления период квантования определяется из соотношения

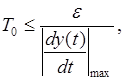(1.5)

где 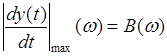- характеристика, т.е. для определения периода квантования необходимо иметь информацию о возможных изменениях скоростей входной управляющей координаты объекта.

Для типичных звеньев систем автоматического регулирования значения B() - характеристики приведены в табл. 1.1.

Таблица 1.1 – Значения В – характеристики для типичных звеньев систем

Рассмотрим следующий пример.

Определить оптимальный период квантования в системе НЦУ, если объект управления имеет передаточную функцию

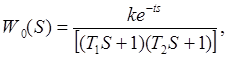
в которой k = 1.2; T₁ = 30с; T₂ = 10c; t = 5c.

Задана абсолютная погрешность исходного сигнала объекта, которая возникает от квантования по времени

= 0.155.

Согласно табл. 1.1 выбираем передаточную функцию объекта

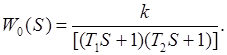
Так как на величину B -характеристики инерционность объекта не влияет, то максимальное её значение будет

.

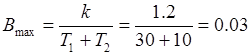Определим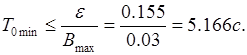

Принимаем T₀ = 5c.

Приведенные критерии выбора периода квантования не могут применяться для объектов управления, которые описываются дифференциальными уравнениями, с производными в правой части, или если в числителе передаточных функций имеется производная процесса. Рассмотрим критерий воспроизведения частотных составляющих в сигнале на выходе объекта, который имеет передаточную функцию

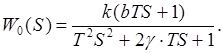
Передаточную функцию объекта путем подстановок приводят к виду

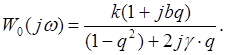
Приравнивая значение модуля к величине 1/ при , получим

.

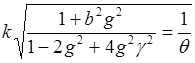Определяем из полученного выражения значение . Величина характеризует ослабление гармонической составляющей сигнала с частотой (на практике = 31). После решения уравнения находим

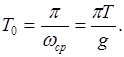
1.4. Типичные алгоритмы непосредственно цифрового управления (НЦУ)

На базе СВТ можно реализовывать сложные и эффективные законы управления и регулирования. При построении алгоритмов управления технологическими процессами на базе СВТ исходят из принципов действия хорошо исследованных регуляторов: пропорционального (П), интегрального (И), пропорционально-интегрального (ПИ) и пропорционально-интегрально-дифференциального (ПИД).

Закон управления аналогового ПИД-регулятора можно представить уравнением

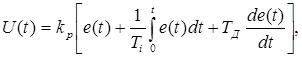(1.6)

где - управляющее воздействие;

e(t) - отклонение регулируемой величины от заданного значения;

К_р - коэффициент усиления;

Т_Д - постоянная времени дифференцирования;

Ті - постоянная времени интегрирования.

Заменим непрерывные функции e(t) решётчатыми функциями

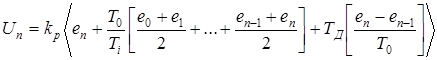. (1.7)

Для реализации дискретных ПИД-законов управления разработано ряд широко используемых алгоритмов.

Позиционный алгоритм основан на расчете полной величины управляющего воздействия

(1.8)

где .

Рассмотрим алгоритм работы цифрового ПИД-регулятора, проанализировав каждую его составляющую отдельно.

Пропорциональная составляющая на n-м периоде квантования может рассматриваться автономно в алгоритме позиционного управления

(1.9)

Интегральная составляющая в позиционном алгоритме, исходя из трапецеидального правила для числового интегрирования, имеет вид

(1.10)

Применяя другой способ представления интегральной составляющей, получим

(1.11)

Сигнал на выходе идеального дифференциального звена для позиционного алгоритма в дискретной форме имеет вид

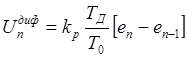. (1.12)

Согласно используемым формулам (1.9-1.12), управляющее воздействие при позиционном алгоритме принимает вид

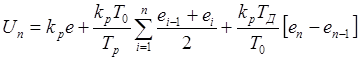. (1.13)

Вычтем с обеих частей уравнения (1.13.) величину Un-1, в результате чего получим

(1.14)

Это уравнение можно привести к виду

(1.15)

Введём обозначения:

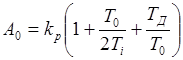, (1.16)

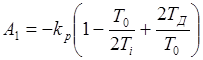, (1.17)

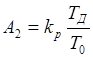. (1.18)

Основное уравнение позиционного алгоритма регулирования имеет вид

(1.19)

Уравнение приведено к форме, удобной для программирования. Оценка коэффициентов А₀, А₁, А₂ эквивалентна оценке величин k_p, T_i, T_Д при постоянном T₀.

На основании полученных выражений для конкретных условий работы рассчитывается полная величина управляющего воздействия на заданном T₀, она передается на ЦАП и на исполнительное устройство.

Скоростной алгоритм отличается тем, что исходный сигнал представляет собой производную, или скорость действия управляющеговоздействия, и является следствием дифференцирования позиционного алгоритма и реализуется с помощью общей работы цифрового регулятора и исполнительного механизма. Интегрирование осуществляется исполнительным механизмом (например, интегральным операционным усилителем с цифровым выходом).

При скоростном алгоритме на каждом периоде квантования определяется прирост управляющего воздействия

. (1.20)

Аналогично позиционному алгоритму пропорциональная составляющая управляющего воздействия при скоростном алгоритме имеет вид

(1.21)

На основе уравнения (1.11) находим выражение для прироста интегральной составляющей

(1.22)

Сигнал на выходе интегрально-дифференциального звена для скоростного алгоритма на основе выражения (1.13) можно записать в следующем виде

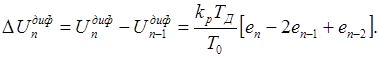(1.23)

Для цифровых систем характерно постоянное значение величины G=const регулятора на определенном промежутке времени. Принимая во внимание е_п =G_n -Y_n, представим скоростной алгоритм в следующем виде

(1.24) из которого видно, что задача влияния регулятора G присутствует только в приросте интегральной составляющей. Если интегральную составляющую исключить, то невозможно предотвратить дрейф регулятора.

В реальных условиях вследствие действия помех дифференциальная составляющая управляющего воздействия на выходе системы принимает большее значение за счет скачкообразных приростов погрешности несогласованности е_n = G_n -Y_n.

Для уменьшения влияния высокочастотных помех применяются разные способы фильтрации дифференциальной составляющей.

Первым способом фильтрации является применение реального дифференциального звена с постоянной времени T_ф = ( 10-100)T₀. Сигнал на выходе такого звена в аналоговой форме можно представить в виде

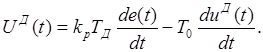(1.25)

В дискретной форме при позиционном алгоритме он примет вид

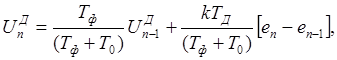(1.26)

а при скоростном алгоритме

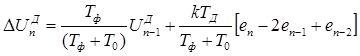. (1.27)

Кроме ввода постоянной времени фильтра , для уменьшения влияния помехи разработан другой способ дифференцирования в дискретной форме по четырем точкам. Пусть средняя величина исходной переменной, которая регулируется за четыре попытки опрашивания, равняется

(1.28)

Тогда

.(1.29)

Влияние помех снижается за счёт усреднения переменной, которая управляется. Вычисление дифференциальной составляющей в дискретной форме осуществляется на основе учета предыстории измерений у.

Принимая во внимание (1.29), скоростной алгоритм управления представим в виде

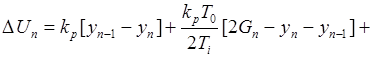
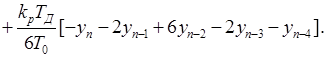(1.30)

Список литературы

1. Промышленные приборы и средства автоматизации: Справочник/Под ред. В.В.Черепковой - Л.: Машиностроение, 1987.

2. Строганов Р.П. Управляющие машины и их применение. - М., 1986.

3. Романенко В.Д., Игнатенко Б.В. Адаптивное управление технологическими процессами на базе микро-ЭВМ. - К.: Высшая школа, 1990.