В предыдущих главах мы подразумевали, что у канала отсутствует память, поскольку рассматривались коды, которые должны были противостоять случайным независимым ошибкам. Канал с памятью — это такой канал, в котором проявляется взаимная зависимость ухудшений передачи сигнала. Канал, в котором проявляется замирание вследствие многолучевого распространения, когда сигнал поступает на приемник по двум или более путям различной длины, есть примером канала с памятью. Следствием является различная фаза сигналов, и в итоге, суммарный сигнал оказывается искаженным. Таким эффектом обладают каналы мобильной беспроводной связи, так же как ионосферные и тропосферные каналы. (Более подробно о замирании см. главу 15.) В некоторых каналах также имеются коммутационные и другие импульсные помехи (например, телефонные каналы или каналы с создаваемыми импульсными помехами). Все эти ухудшения коррелируют во времени и, в результате, дают статистическую взаимную зависимость успешно переданных сигналов. Иными словами, искажения вызывают ошибки, имеющие вид пакетов, а не отдельных изолированных ошибок.
Если канал имеет память, то ошибки не являются независимыми, одиночными и случайно распределенными. Большинство блочных и сверточных кодов разрабатывается для борьбы с независимыми случайными ошибками. Влияние канала с памятью на кодированный таким образом сигнал приведет к ухудшению достоверности передачи. Существуют схемы кодирования для каналов с памятью, но наибольшую проблему в этом кодировании представляет расчет точных моделей сильно нестационарных статистик таких каналов. Один подход, при котором требуется знать только объем памяти канала, а не его точное статистическое описание, использует временное разнесение, или чередование битов.
Чередование битов кодированного сообщения перед передачей и обратная операция после приема приводят к рассеиванию пакета ошибок во времени: таким образом, они становятся для декодера случайно распределенными. Поскольку в реальной ситуации память канала уменьшается с временным разделением, идея, лежащая в основе метода чередования битов, заключается в разнесении символов кодовых слов во времени. Получаемые промежутки времени точно так же заполняются символами других кодовых слов. Разнесение символов во времени эффективно превращает канал с памятью в канал без памяти и, следовательно, позволяет использовать коды с коррекцией случайных ошибок в канале с импульсными помехами.
Устройство чередования смешивает кодовые символы в промежутке нескольких длин блоков (для блочных кодов) или нескольких длин кодового ограничения (для сверточных кодов). Требуемый промежуток определяется длительностью пакета., Подробности структуры битового перераспределения должны быть известны приемнику, чтобы иметь возможность выполнить восстановление порядка битов перед декодированием. На рис. 8.10 показан простой пример чередования. На рис. 8.10, а мы можем видеть кодовые слова, которые еще не подвергались описанной операции, от A до G. Каждое кодовое слово состоит из семи кодовых символов. Пусть наш код может исправлять однобитовые ошибки в любой 7-символьной последовательности. Если промежуток памяти канала равен длительности одного кодового слова, такой пакет, длительностью в семь символов, может уничтожить информацию в одном или двух кодовых словах. Тем не менее допустим, что после получения кодированных данных кодовые символы затем перемешиваются, как показано на рис. 8.10, б. Иными словами, каждый кодовый символ каждого кодового слова отделяется от своего соседа на расстояние из семи символьных периодов. Полученный поток затем преобразуется в модулированный сигнал и передается по каналу. Как можно видеть на рис. 8.10, 6, последовательные канальные пакеты шума попадают на семь символьных промежутков, влияя на один кодовый символ каждого из семи исходных кодовых слов. Во время приема в потоке вначале восстанавливается исходный порядок битов, так что он становится похож на исходную кодированную последовательность, изображенную на рис. 8.10, а. Затем поток декодируется. Поскольку в каждом кодовом слове возможно исправление одиночной ошибки, импульсная помеха не оказывает никакого влияния на конечную последовательность.
Идея чередования битов используется во всех блочных и сверточных кодах, рассмотренных здесь и ранее в предыдущих главах. Обычно применяются два типа устройств чередования — блочные и сверточные (оба рассматриваются далее).
8.2.1. Блочное чередование
Блочное устройство чередования принимает кодированные символы блоками от кодера, переставляет их, а затем передает измененные символы на модулятор. Как правило, перестановка блоков завершается заполнением столбцов матрицы М строками и N столбцами (
) кодированной последовательности. После того как матрица полностью заполнена, символы подаются на модулятор (по одной строке за раз), а затем передаются по каналу. В приемнике устройство восстановления выполняет обратные операции; оно принимает символы из демодулятора, восстанавливает исходный порядок битов и передает их на декодер. Символы поступают в массив устройства восстановления по строкам и заменяются столбцами. На рис. 8.11, а приведен пример устройства чередования с М = 4 строками и N = 6 столбцами. Записи в массиве отображают порядок, в котором 24 кодовых символа попадают в устройство чередования. Выходная последовательность, предназначенная для передатчика, состоит из кодовых символов, которые построчно удалены из массива, как показано на рисунке. Ниже перечисляются наиболее важные характеристики такого блочного устройства.
1. Пакет, который содержит меньше N последовательных канальных символов, дает на выходе устройства восстановления исходного порядка символов ошибки, разнесенные между собой, по крайней мере, на М символов.
2. Пакет из bN ошибок, где 
, дает на выходе устройства восстановления пакет, который содержит не меньше [b] символьных ошибок. Каждый из пакетов ошибок отделен от другого не меньше, чем на 
символов. Запись [x] означает наименьшее целое число, не меньшее х, а запись [x] — наибольшее целое число, не превышающее х.
3. Периодическая последовательность одиночных ошибок, разделенных N символами, дает на выходе устройства восстановления одиночные пакеты ошибок длиной М.
4. Прямая задержка между устройствами чередования и восстановления равна приблизительно длительности 2MN символов. Если быть точным, перед тем как начать передачу, нужно заполнить лишь 
ячеек памяти (как только будет внесен первый символ последнего столбца массива ). Соответствующее время нужно приемнику, чтобы начать декодирование. Значит, минимальная прямая задержка будет составлять длительность 
символов, не учитывая задержку на передачу по каналу.
5. Необходимая память составляет MN символов для каждого объекта (устройств чередования и восстановления исходного порядка). Однако массив нужно заполнить (по большей части) до того, как он будет считан. Для каждого объекта нужно предусмотреть память для 2MN символов, чтобы опорожнить массив , пока другой будет наполняться, и наоборот.
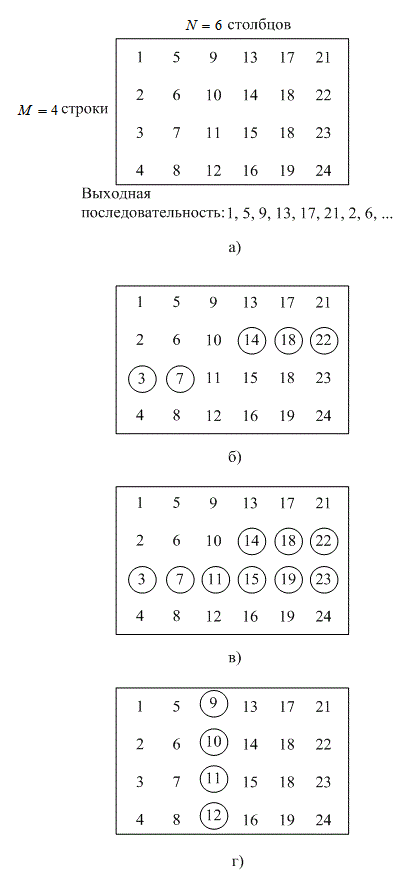
Пример 8.4. Характеристики устройств чередования
Используя структуру устройства чередования с M = 4, N = 6, изображенную на рисунке 8.11, a, проверьте описанные выше характеристики.
Решение
1.Пусть имеется пакет шума длительностью в пять символьных интервалов; так, что символы, выделенные на рис. 8.11,б, подвергнуться искажению во время передачи. После восстановления исходного порядка битов в приемнике, последовательность принимает следующий вид.
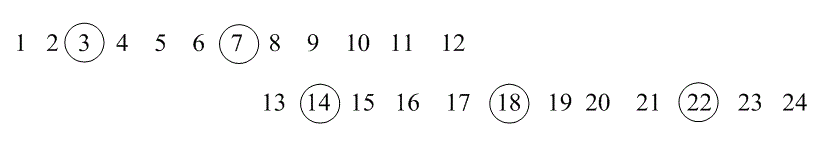
Здесь выделенные символы являются ошибочными. Можно видеть, что, минимальное расстояние, разделяющее символы с ошибками, равно M = 4.
2.Пусть b = 1,5, так что bN = 9. Пример девятисимвольного пакета ошибок можно видеть на рис. 8.11, в. После того как в приемнике проведена процедура восстановления исходного порядка, последовательность примет следующий виц.
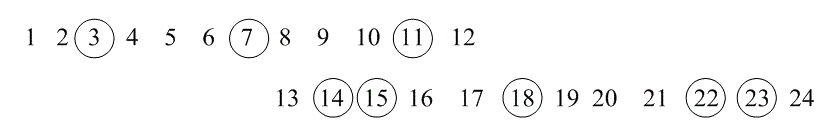
Снова выделенные символы являются ошибочными. Здесь можно видеть, что пакеты содержат не больше [1,5] = 2 символов подряд и разнесены, по крайней мере, на [1,5] = 4 – 1 = 3 символа.
3.На рис. 8.11, г показана последовательность одиночных ошибок, разделенных (каждый по отдельности) N = 6 символами. После восстановления исходного порядка в приемнике, последовательность принимает следующий вид.
Можно видеть, что после этого последовательность содержит пакет одиночных ошибок длиной M = 4 символа.
4. Прямая задержка: минимальная прямая задержка, вызванная обоими устройствами, составляет 
символьных периода.
5. Требуемый объем памяти: размерность массивов устройств чередования и восстановления составляет . Значит, требуется объем памяти для хранения MN = 24 символов на обоих концах канала. Как упоминалось ранее, в общем случае память реализуется для хранения 2MN = 48 символов.
Как правило, параметры устройства чередования, используемого совместно с кодом с коррекцией одиночных ошибок, выбираются таким образом, чтобы число столбцов N превышало ожидаемую длину пакета. Выбираемое число строк зависит от того, какая схема кодирования будет использована. Для блочных кодов М должно быть больше длины кодового блока; для сверточных кодов М должно превышать длину кодового ограничения. Поэтому пакет длиной N может вызвать в блоке кода (самое большее) одиночную ошибку; аналогично в случае сверточных кодов в пределах одной длины кодового ограничения будет не более одной ошибки. Для кодов с коррекцией ошибок кратности t, выбираемое N должно лишь превышать ожидаемую длину пакета, деленную на t.
8.2.2. Сверточное чередование
Сверточные устройства чередования были предложены Рамси (Ramsey) [7] и Форни (Forney) [8]. Схема, предложенная Форни, показана на рис. 8.12. Кодовые символы послдовательно подаются в блок из N регистров; каждый последующий регистр может хранить на J символов больше, чем предыдущий. Нулевой регистр не предназначен для хранения (символ сразу же передается). С каждым новым кодовым символом коммутатор переключается на новый регистр, и кодовый символ подается на него до тех пор, пока наиболее старый кодовый символ в регистре не будет передан на модулятор/передатчик. После 
-го регистра коммутатор возвращается к нулевому регистру и повторяет все снова. После приема операции повторяются в обратном порядке. И вход, и выход устройств чередования и восстановления должны быть синхронизированы.
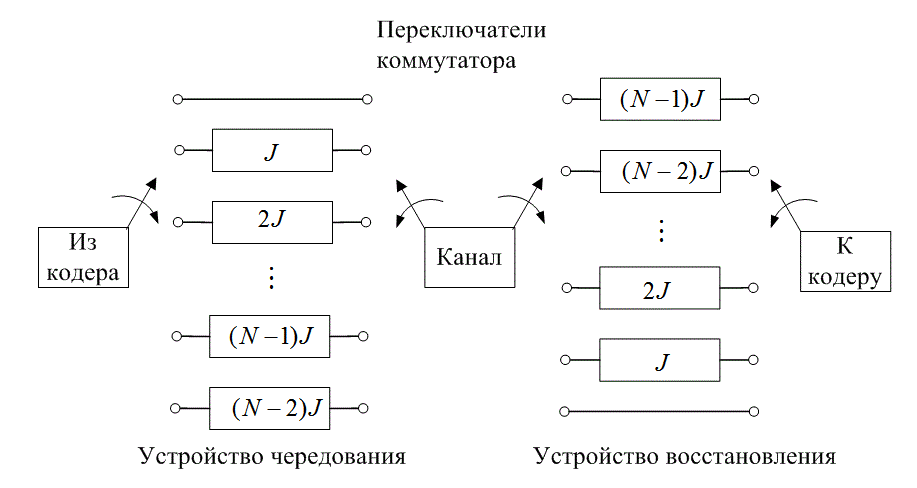
Рис. 8. 12. Реализация регистра сдвига для сверточного устройства чередования/восстановления
На рис. 8.13 показан пример простого сверточного четырехрегистрового (У= 1) устройства чередования, загруженного последовательностью кодовых символов. Одновременно представлено синхронизированное устройство восстановления, которое передает обработанные символы на декодер. На рис. 8.13, а показана загрузка символов 1-4; знак "х" означает неизвестное состояние. На рис. 8.13, б представлены первые четыре символа, подаваемые в регистры, и показана передача символов 5—8 на выход устройства чередования. На рис. 8.13, в показаны поступающие в устройство символы 9—12. Теперь устройство восстановления заполнено символами сообщения, но еще не способно ничего передавать на декодер. И наконец, на рис. 8.13, г показаны символы 13-16, поступившие в устройство чередования, и символы 1—4, переданные на декодер. Процесс продолжается таким образом до тех пор, пока полная последовательность кодового слова не будет передана на декодер в своей исходной форме.
Рабочие характеристики сверточного устройства чередования сходны с параметрами блочного устройства. Важным преимуществом сверточного устройства перед блочным является то, что при сверточном чередовании прямая задержка составляет M(N-l) символов при M = NJ, а требуемые объемы памяти— 
на обоих концах канала. Очевидно, что требования к памяти и время задержки снижаются вдвое, по сравнению с блочным чередованием [9].
8.2.3. Каскадные коды
Каскадными называются коды, в которых кодирование осуществляется в два уровня; имеется внутренний и внешний коды, с помощью которых и достигается желаемая надежность передачи сообщений. На рис. 8.14 изображен порядок кодирования и декодирования. Внутренний код связан с модулятором. Демядулятор, как правило, настраивается для исправления большинства канальных ошибок. Внешний код, чаще всего высокоскоростной (с низкой избыточностью), снижает вероятность появления ошибок до заданного значения. Основной причиной использования каскадного кода является низкая степень кодирования и общая сложность реализации, меньшая той, которая потребовалась бы для осуществления отдельной процедуры кодирования. На рис. 8.14 между двумя этапами кодирования располагается устройство чередования. Обычно это делается для того, чтобы разнести пакетные ошибки, которые могли бы появиться в результате внутреннего кодирования.
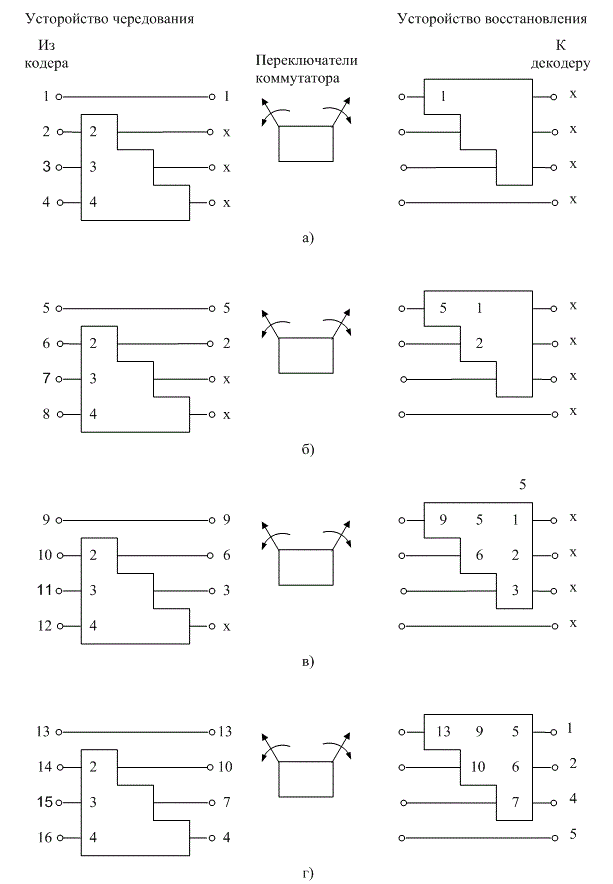
Рис. 8.13. Пример сверточного чередования/восстановления
В одной из наиболее популярных систем каскадного кодирования для внутреннего кода применяется сверточное кодирование по алгоритму Витерби, а для внешнего — код Рида-Соломона с чередованием между двумя этапами кодирования [2]. Функционирование таких систем при 
, находящемся в пределах от 0,2 до 2,5 дБ, для достижения 
реально достижимо в прикладных задачах [9]. В этой системе демодулятор выдает мягко квантованные кодовые символы на внутренний свёрточный декодер, который, в свою очередь, выдает жестко квантованные кодовые символы с пакетными ошибками на декодер Рида-Соломина.
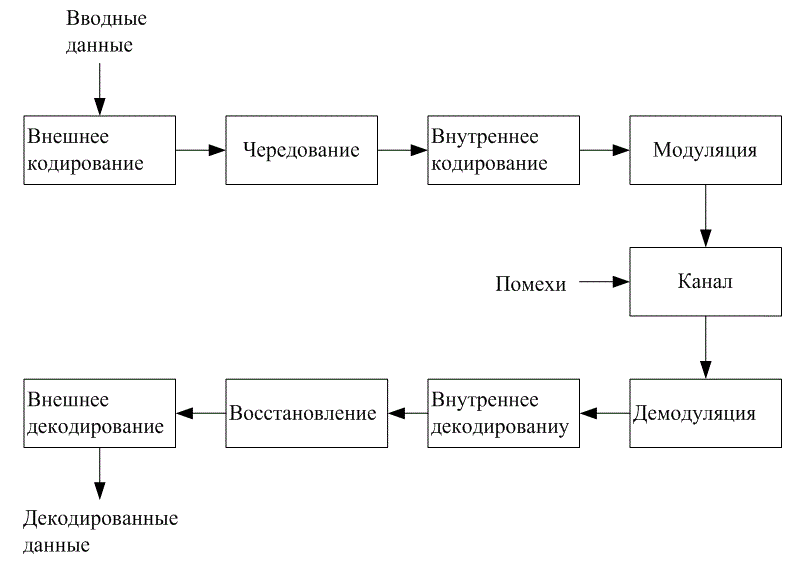
Рис. 8.14. Блочная диаграмма каскадной системы кодирования
(В системе декодирования по алгоритму Витерби выходные ошибки имеют тенденцию к появлению пакетами.) Внешний код Рида-Соломона образуется из m-битовых сегментов двоичного потока данных. Производительность такого (недвоичного) кода Рида-Соломона зависит только от числа символьных ошибок в блоке. Код не искажается пакетами ошибок внутри m-битового символа. Иными словами, для данной символьной ошибки производительность кода Рида-Соломона такова, как если бы символьная ошибка была вызвана одним битом или т бит. Тем не менее производительность каскадных систем несколько ухудшается за счет коррелирующих ошибок в последовательных символах. Поэтому чередование между кодированиями нужно выполнять на уровне символов (а не битов). Работа [10] представляет собой обзор каскадных кодов, которые были разработаны для дальней космической связи.