3.3.1. Формирование импульсов с целью снижения ISI

3.3.1.1. Цели и компромиссы

3.3.1.2. Фильтр с характеристикой типа приподнятого косинуса

3.3.2. Факторы роста вероятности ошибки

3.3.3. Демодуляция/обнаружение сформированных импульсов

3.3.3.1. Согласованные и обычные фильтры

3.3.3.2. Импульсы Найквиста

На рис. 3.15, а представлены фильтрующие элементы типичной системы цифровой связи. В системе - передатчике, приемнике и канале - используется множество разнообразных фильтров (и реактивных элементов, таких как емкость и индуктивность). В передатчике информационные символы, описываемые как импульсы или уровни напряжения, модулируют импульсы, которые затем фильтруются для согласования с определенными ограничениями полосы. В узкополосных системах канал (кабель) имеет распределенное реактивное сопротивление, искажающее импульсы. Некоторые полосовые системы, такие как беспроводные, являются, по сути, каналами с замираниями (см. главу 15), которые проявляют себя как нежелательные фильтры, также искажающие сигнал. Если принимающий фильтр настраивается на компенсацию искажения, вызванного как передатчиком, так и каналом, он зачастую называется выравнивающим (equalizing filter) или принимающим/выравнивающим (receiving/equalizing). На рис. 3.15, б приведена удобная модель системы, объединяющая все следствия фильтрации в одну общесистемную передаточную функцию.

(3.77)

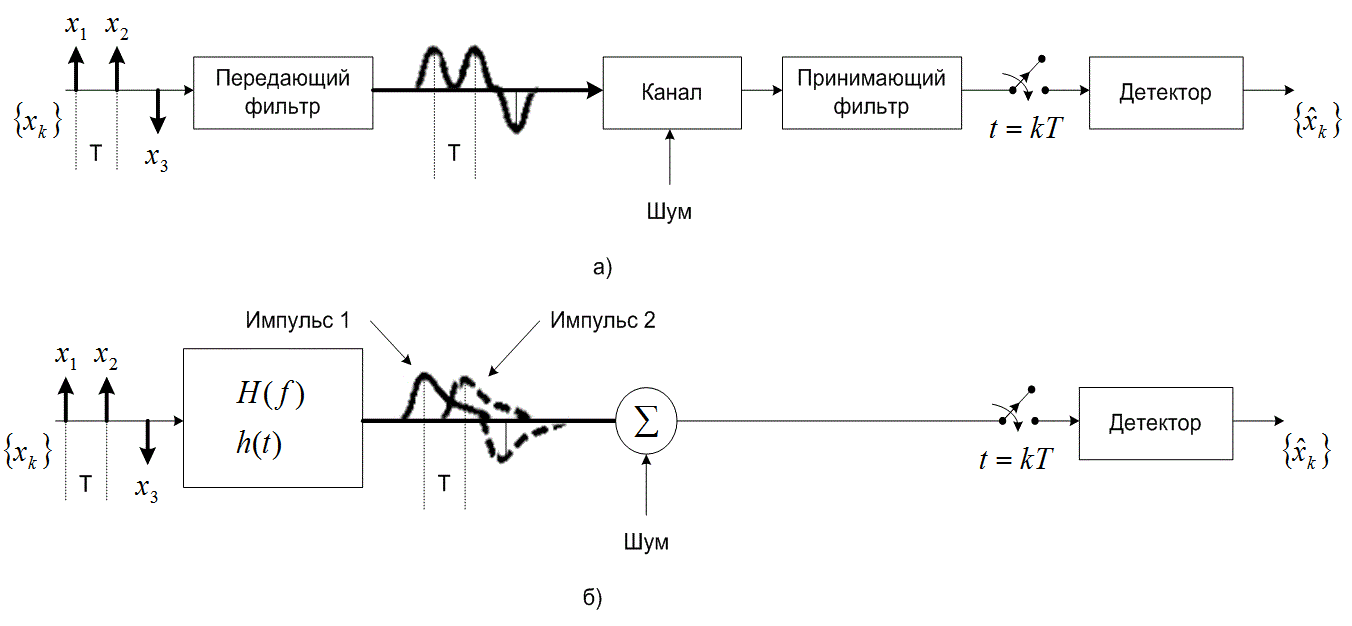
Рис.3.15. Межсимвольная интерференция в процессе обнаружения:

а) типичная узкополосная цифровая система; б) эквивалентная модель

Здесь характеризует передающий фильтр, - фильтрацию в канале, а - принимающий/выравнивающий фильтр. Таким образом, характеристика представляет передаточную функцию всей системы, отвечающую за все этапы фильтрации в различных местах цепочки передатчик-канал-приемник. В бинарной системе, использующей какую-нибудь распространенную кодировку РСМ, например NRZ-L, детектор принимает решение относительно значения символа путем сравнения выборки принятого импульса с порогом. Например, детектор, изображенный на рис. 3.15, решает, что была послана двоичная единица, если принятый импульс положителен, или двоичный нуль - в противном случае. Вследствие системной фильтрации принятые импульсы могут перекрываться, как показано на рис. 3.15, б. Хвост импульса может «размываться» на соседний интервал передачи символа, таким образом мешая процессу обнаружения и повышая вероятность появления ошибки; подобный процесс получил название межсимвольной интерференции (intersymbol interference - ISI). Даже при отсутствии шумов воздействие фильтрации и искажение, вызванное каналом, приводят к возникновению ISI. Иногда функция задается, и задача состоит в определении и , минимизирующих ISI на выходе .

Исследованием проблемы задания формы принятого импульса с тем, чтобы предотвратить появление ISI на детекторе, долгое время занимался Найквист [6]. Он показал, что минимальная теоретическая ширина полосы системы, требуемая для определения символов/секунду без ISI, равна Гц. Это возможно, если передаточная функция системы имеет прямоугольную форму, как показано на рис. 3.16, а. Для узкополосных систем с такой , что односторонняя ширина полосы фильтра равна 1/2T (идеальный фильтр Найквиста), импульсная характеристика функции , вычисляемая с помощью обратного преобразования Фурье (см. табл. А.1), имеет вид ; она показана на рис. 3.16, б. Импульс, описываемый функцией , называется идеальным импульсом Найквиста; он имеет бесконечную длительность и состоит из множественных лепестков: главного и боковых, именуемых хвостами. Найквист установил, что если каждый импульс принятой последовательности имеет вид , импульсы могут обнаруживаться без межсимвольной интерференции. На рис. 3.16, б показано, как удается обойти ISI. Итак, имеем два последовательных импульса, и . Несмотря на то что хвосты функции имеют бесконечную длительность, из рисунка видно, что в момент взятия выборки функции хвост функции проходит через точку нулевой амплитуды, и подобным образом он будет иметь нулевую амплитуду в моменты взятия выборок всех остальных импульсов последовательности , . Следовательно, предполагая идеальную синхронизацию процесса взятия выборок, получаем, что межсимвольная интерференция не будет влиять на процесс обнаружения. Чтобы узкополосная система могла обнаруживать 1/Т таких импульсов (символов) в секунду, ширина ее полосы должна быть равна 1/2T; другими словами, система с шириной полосы Гц может поддерживать максимальную скорость передачи символов/с (ограничение полосы по Найквисту) без ISI. Следовательно, при идеальной фильтрации Найквиста (и нулевой межсимвольной интерференции) максимальная возможная скорость передачи символов на герц полосы, называемая уплотнением скорости передачи символов (symbol-rate packing), равна 2 символа/с/Гц. Вследствие прямоугольной формы передаточной функции идеального фильтра Найквиста и бесконечной длины соответствующего импульса, подобные идеальные фильтры нереализуемы; реализовать их можно только приближенно.

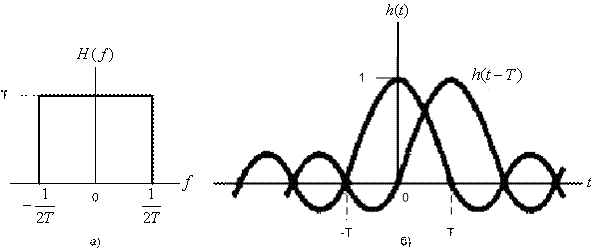
Рис. 3.16. Каналы Найквиста для нулевой межсимвольной интерференции:

а) прямоугольная передаточная функция системы ;

б) принятый импульс

Стоит отметить, что названия «фильтр Найквиста» и «импульс Найквиста» часто используются для описания обширного класса фильтраций и формообразований, удовлетворяющих условию нулевой межсимвольной интерференции в точках взятия выборок. Фильтр Найквиста - это фильтр, передаточная функция которого может быть представлена прямоугольной функцией, свернутой с любой четно-симметричной частотной функцией. Импульс Найквиста - это импульс, форма которого может быть описана функцией , умноженной на другую временную функцию. Следовательно, существует бесконечное множество фильтров Найквиста и соответствующих импульсов. В классе фильтров Найквиста наиболее популярными являются фильтры с характеристикой типа приподнятого косинуса или корня из приподнятого косинуса. Несколько позже эти фильтры будут рассмотрены подробно.

Основным параметром систем связи является эффективность использования полосы, , измеряемая в бит/с/Гц. Как можно понять из единиц измерения, представляет меру скорости переноса данных на единицу ширины полосы, а значит, показывает, насколько эффективно любой метод передачи сигналов использует ресурс полосы. Поскольку ограничение ширины полосы по Найквисту устанавливает теоретическое максимальное уплотнение скорости передачи символов без межсимвольной интерференции, равное 2 символа/с/Гц, может возникнуть вопрос, можно ли что-то сказать об ограничении величин, измеряемых в бит/с/Гц. О последних ничего нельзя сказать прямо; ограничение связано только с импульсами или символами и возможностью обнаружения их амплитудных значений без искажения со стороны других импульсов. При нахождении для любой схемы передачи сигналов необходимо знать, сколько битов представляет каждый символ, что само по себе является темой отдельного рассмотрения. Допустим, сигналы кодируются с использованием М-уровневой кодировки РАМ. Каждый символ (включающий бит) представляется одной из М импульсных амплитуд. Для бит на символ размер набора символов составляет амплитуды. Таким образом, при 64-уровневой кодировке РАМ теоретическая максимальная эффективность использования полосы, не допускающая межсимвольной интерференции, равна 12 бит/с/Гц. (Подробнее об эффективности использования полосы в главе 9.)

3.3.1. Формирование импульсов с целью снижения ISI

3.3.1.1. Цели и компромиссы

Чем компактнее спектр передачи сигналов, тем выше разрешенная скорость передачи данных или больше число пользователей, которые могут обслуживаться одновременно. Это имеет большое значение для поставщиков услуг связи, поскольку более эффективное использование доступной ширины полосы приносит больший доход. Для большинства систем связи (за исключением систем расширенного спектра, рассмотренных в главе 12) нашей задачей является максимальное сужение требуемой полосы системы. Найквист определил основное ограничение для такого сужения полосы. Но что произойдет, если заставить систему работать с меньшей полосой, чем определяется ограничением? Импульсы станут протяженнее по времени, что, вследствие увеличения межсимвольной интерференции, отрицательно скажется на достоверности передачи. Более разумным было бы сжатие полосы информационных импульсов до некоторого разумного значения, которое больше минимума, определенного Найквистом. Это выполняется путем формирования импульсов с помощью фильтра Найквиста. Если край полосы пропускания фильтра крутой, приблизительно соответствующий прямоугольной форме (рис. 3.16, а), то спектр сигнала можно сделать более компактным. В то же время использование подобного фильтра приводит к тому, что длительность импульсного отклика становится приблизительно равна бесконечности, как показано на рис. 3.16, б. Каждый импульс накладывается на все импульсы последовательности. Длительные отклики дают хвосты больших амплитуд около главного лепестка каждого импульса. Подобные хвосты нежелательны, поскольку, как видно из рис. 3.16, б, они вносят нулевую межсимвольную интерференцию только в том случае, если выборка производится точно в соответствующий момент времени; при больших хвостах даже небольшие ошибки синхронизации приведут к межсимвольной интерференции. Следовательно, хотя компактный спектр и позволяет оптимальным образом использовать полосу, он оказывается очень чувствительным к ошибкам синхронизации, приводящим к увеличению межсимвольной интерференции.

3.3.1.2. Фильтр с характеристикой типа приподнятого косинуса

Ранее говорилось, что принимающий фильтр часто называется выравнивающим, если он настраивается на компенсацию искажений, вносимых передатчиком и каналом. Другими словами, конфигурация этого фильтра выбрана так, чтобы оптимизировать общесистемную частотную передаточную функцию , описанную формулой (3.77). Одна из часто используемых передаточных функций принадлежит к классу функций Найквиста (нулевая ISI в моменты взятия выборок) и называется приподнятым косинусом (raised-cosine). Описывается эта функция следующим выражением.

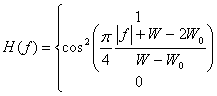
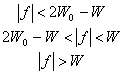(3.78)

Здесь W - максимальная ширина полосы, a - минимальная ширина полосы по Найквисту для прямоугольного спектра и ширина полосы по уровню -6 дБ (или точка половинной амплитуды) для косинусоидального спектра. Разность называется «избытком полосы» (excess bandwidth); она означает дополнительную ширину полосы по сравнению с минимумом Найквиста (например, для прямоугольного спектра ). Коэффициент сглаживания (roll-off factor) определяется как , где . Коэффициент сглаживания - это избыток полосы, деленный на ширину полосы по уровню -6 дБ (т.е. относительный избыток полосы). Для данного выравнивание задает требуемый избыток относительно и характеризует крутизну фронта характеристики фильтра. На рис. 3.17, а для нескольких значений коэффициента сглаживания (, и ) показана характеристика типа приподнятого косинуса. Случай соответствует минимальной ширине полосы по Найквисту. Отметим, что при требуемый избыток полосы равен 100% и хвосты характеристики достаточно малы. Система с подобной спектральной характеристикой может поддерживать скорость передачи символов символов/с при использовании полосы в , Гц (удвоенная минимальная полоса по Найквисту), что дает уплотнение скорости передачи, равное 1 символ/с/Гц. Импульсный отклик, соответствующий функции и определяемый выражением (3.78), равен следующему.

(3.79)

Этот импульсный отклик изображен на рис. 3.17, б для , и . Хвост имеет нулевые значения в каждый момент взятия выборки, вне зависимости от значения коэффициента сглаживания.

Фильтр, описанный уравнением (3.78), и импульс, представленный уравнением (3.79), можно реализовать только приблизительно, поскольку, строго говоря, спектр типа приподнятого косинуса физически не может быть реализован (причина та же, что и при реализации идеального фильтра Найквиста). Реализуемый фильтр должен иметь импульсный отклик конечной длительности и давать нулевой выход до момента включения импульса (см. раздел 1.7.2), что невозможно для семейства характеристик типа приподнятого косинуса. Эти нереализуемые фильтры являются непричинными (импульсный отклик фильтра имеет бесконечную продолжительность и фильтрованный импульс начинается в момент ). На практике фильтр формирования импульсов должен удовлетворять двум требованиям. Он должен обеспечивать желаемое сглаживание и должен быть реализуем (импульсный отклик должен усекаться до конечного размера).

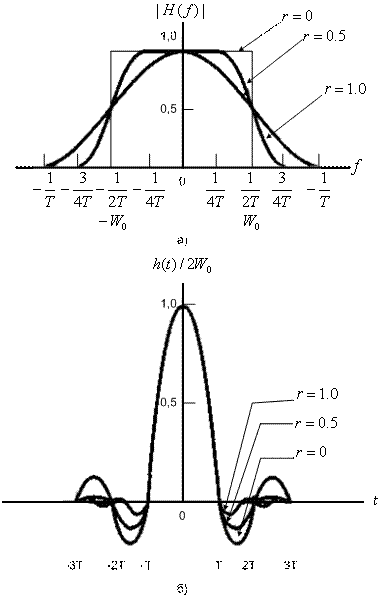
Рис. 3.17. Характеристики фильтров типа приподнятого косинуса:

а) передаточная функция системы; б) импульсный отклик системы

Используя ограничение ширины полосы по Найквисту (минимальная ширина полосы W, требуемая для поддержания скорости символов/с без межсимвольной интерференции, равна Гц), можно вывести более общее соотношение между требуемой полосой и скоростью передачи символов, включающее коэффициент сглаживания .

(3.80)

Таким образом, при формула (3.80) описывает минимальную требуемую полосу для обеспечения идеальной фильтрации по Найквисту. При ширина полосы превышает минимум Найквиста; следовательно, для этого случая меньше удвоенной ширины полосы. Если демодулятор подает на выход одну выборку на символ, теорема о дискретном представлении Найквиста нарушается, поскольку у нас остается слишком мало выборок для однозначного восстановления аналогового сигнала (присутствует наложение). Впрочем, в системах цифровой связи нас и не интересует восстановление аналоговых сигналов. Кроме того, поскольку семейство фильтров с характеристикой типа приподнятого косинуса характеризуется нулевой межсимвольной Интерференцией в каждый момент произведения выборки из символа, мы по-прежнему можем добиться однозначного обнаружения.

Сигналы с полосовой модуляцией (см. главу 4), такие как сигналы с амплитудной (amplitude-shift keying - ASK) и фазовой манипуляцией (phase-shift keying - PSK), требуют вдвое большей полосы передачи, чем эквивалентные узкополосные сигналы (см. раздел 1.7.1). Такие смещенные по частоте сигналы занимают полосу, вдвое большую по ширине соответствующей узкополосной; зачастую их называют двухполосными (double-sideband - DSB). Следовательно, для сигналов в кодировках ASK и PSK соотношение между требуемой шириной полосы и скоростью передачи символов принимает следующий вид.

(3.81)

Напомним, что передаточная функция, имеющая вид приподнятого косинуса, - это общесистемная функция , описывающая «полный проход» сообщения, отправленного передатчиком (в виде импульса), через канал и принимающий фильтр. Фильтрация в приемнике описывается частью общей передаточной функции, тогда как подавление межсимвольной интерференции обеспечивает передаточная функция, имеющая вид приподнятого косинуса. Как следствие сказанного, принимающий и передающий фильтры часто выбираются (согласовываются) так, чтобы передаточная функция каждого имела вид квадратного корня из приподнятого косинуса. Подавление любой межсимвольной интерференции, внесенной каналом, обеспечивает произведение этих двух функций, которое дает общую передаточную функцию системы, имеющую вид приподнятого косинуса. Если же для уменьшения последствий привнесенной каналом межсимвольной интерференции вводится отдельный выравнивающий фильтр, принимающий и выравнивающий фильтры могут совместно настраиваться так, чтобы компенсировать искажение, вызванное как передатчиком, так и каналом; при этом общая передаточная функция системы характеризуется нулевой межсимвольной интерференцией.

Рассмотрим компромиссы, с которыми приходится сталкиваться при выборе фильтров формирования импульсов. Чем больше сглаживание фильтра, тем короче будут хвосты импульсов (из этого следует, что амплитуды хвостов также будут меньше). Меньшие хвосты менее чувствительны к ошибкам синхронизации, а значит, подвержены меньшему искажению вследствие межсимвольной интерференции. Отметим, что на рис. 3.17, б даже для ошибка синхронизации по-прежнему приводит к некоторому увеличению межсимвольной интерференции. Но в то же время в этом случае проблема менее серьезна, чем при , поскольку при хвосты сигнала больше, чем при . Увеличение хвостов - это плата за повышение избытка полосы. С другой стороны, чем меньше сглаживание фильтра, тем меньше избыток полосы, а это позволяет повысить скорость передачи сигналов или число пользователей, которые могут одновременно использовать систему. Э этом случае мы платим более длительными хвостами импульсов, большими их амплитудами, а следовательно, большей восприимчивостью к ошибкам синхронизации.

3.3.2. Факторы роста вероятности ошибки

Факторы повышения вероятности возникновения ошибки в цифровой связи могут быть следующими. Во-первых, это связано с простым падением мощности принятого сигнала или с повышением мощности шума или интерференции, что в любом случае приводит к уменьшению отношения сигнал/шум, или . Во-вторых, это искажение сигнала, вызванное, например, межсимвольной интерференцией (intersymbol interference - ISI). Ниже показывается, чем отличаются эти факторы.

Предположим, нам нужна система связи с такой зависимостью вероятности появления ошибочного бита от отношения , какая изображена сплошной линией на рис. 3.18, а. Предположим, что после настройки системы и проведения измерений оказывается, к нашему разочарованию, что вероятность соответствует не теоретической кривой, а кривой, показанной на рис. 3.18, а пунктиром. Причина снижения отношения - потеря сигналом мощности или повышение шума или интерференции. Желаемой вероятности ошибочного бита в соответствует теоретическая величина =10 дБ. Поскольку производительность реальной системы не соответствует теоретическим расчетам, нам следует использовать пунктирный график и добиться отношения , равного 12 дБ (для получения той же вероятности ). Если причины проблемы устранить нельзя, то насколько большее отношение требуется теперь для получения необходимой вероятности ошибочного бита? Ответ, разумеется, - 2 дБ. Вообще, это может оказаться серьезной проблемой, особенно если система располагает ограниченной мощностью и получить дополнительные 2 дБ весьма сложно. Но все же уменьшение отношения не смертельно, по сравнению с ухудшением качества, вызванным искажением.

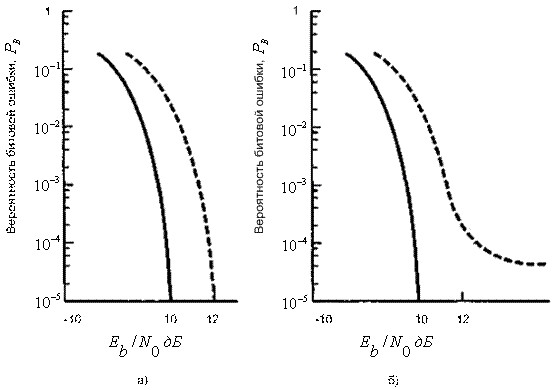
Рис. 3.18. Факторы роста вероятности ошибки: а) снижение ;

б) непреодолимое ухудшение, вызванное искажением

Обратимся к рис 3.18, б и представим, что мы снова не получили желаемой вероятности, описываемой сплошной кривой. Но в этот раз причиной стало не уменьшение отношения сигнал/шум, а искажение, вызванное межсимвольной интерференцией (реальная кривая показана пунктиром). Если причину проблемы устранить нельзя, то насколько большее отношение требуется теперь для получения необходимой вероятности ошибочного бита? В этом случае потребуется бесконечное увеличение. Другими словами, не существует такого , которое позволило бы устранить проблему. Если непреодолимое ухудшение описывается такой кривой, как показана на рис. 3.18, б, то никакое увеличение не может дать желаемого результата (предполагается, что нижняя точка пунктирной кривой находится выше требуемой вероятности ). Безусловно, каждая кривая зависимости от имеет где-то нижнюю точку, но если эта точка находится далеко за областью, представляющей практический интерес, то она уже не имеет значения.

Итак, увеличение отношения не всегда помогает решить проблему межсимвольной интерференции (особенно если кривая зависимости от выходит за область практического интереса). Это можно понять, взглянув на перекрывающиеся импульсы на рис. 3.15, б - увеличение отношения никак не влияет на длительность области перекрытия, и степень искажения импульсов не изменится. Так что же обычно противопоставляют искажающему эффекту межсимвольной интерференции? В данной ситуации наиболее приемлемым является метод, именуемый выравниванием (см. раздел 3.4). Поскольку причиной межсимвольной интерференции является искажение вследствие фильтрации в передатчике и канале, выравнивание можно рассматривать как процесс, компенсирующий подобные неоптимальные эффекты фильтрации.

Пример 3.3. Требования к ширине полосы

а) Найдите минимальную ширину полосы, требуемую для узкополосной передачи последовательности четырехуровневых импульсов в кодировке РАМ со скоростью R=2400 бит/с, если передаточная характеристика системы имеет вид приподнятого косинуса со 100%-ным избытком полосы ().

б) Та же последовательность модулируется несущей, так что теперь узкополосный спектр смещен и центрирован на частоте . Определите минимальную двустороннюю полосу, требуемую для передачи модулированной последовательности РАМ. Передаточная характеристика считается такой же, как и в п. а.

Решение

а) , поскольку М=4 уровня, k=2.

Скорость передачи символов или импульсов символов /с;

минимальная ширина полосы Гц .

На рис. 3.19, а во временной области показан принятый узкополосный импульс в кодировке РАМ; из выражения (3.79) получим функцию . На рис. 3.19, б показан Фурье-образ функции - функция типа приподнятого косинуса. Отметим, что требуемая ширина полосы, W, находится в диапазоне от до ; она вдвое превышает теоретическую минимальную полосу по Найквисту.

б) Здесь, как и в п. а,

символов/с;

Гц.

На рис. 3.20, а показан модулированный принятый импульс. Этот сигнал в кодировке РАМ можно рассматривать как произведение высокочастотной синусоидальной несущей и сигнала с формой импульса, показанной на рис. 3.19, а. Односторонний спектральный график на рис. 3.20, б показывает модулированный сигнал, полоса которого выражается следующей формулой.

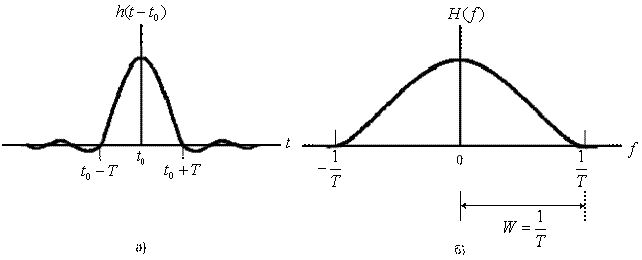
Рис. 3.19. Сформированный импульс и узкополосный спектр типа приподнятого косинуса

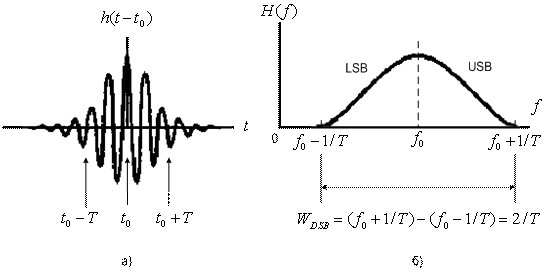
Рис.3.20. Модулированный сформулированный импульс и двухполосный модулированный спектр типа приподнятого косинуса

При смещении вверх по частоте спектра, показанного на рис. 3.19, а, смещаются отрицательная и положительная половины узкополосного спектра, таким образом требуемая полоса передачи дублируется. Как указывает название, двусторонний сигнал имеет две боковые полосы: верхнюю боковую полосу (upper sideband - USB), получаемую из положительной половины узкополосного сигнала, и нижнюю боковую полосу (lower sideband - LSB), получаемую из отрицательной половины.

Пример 3.4. Цифровые телефонные каналы

Сравните требования к ширине полосы системы для наземного аналогового телефонного канала передачи в речевом диапазоне (3 кГц) и цифрового канала. Для цифрового канала речь форматируется как поток битов в кодировке РСМ с частотой дискретизации аналогового сигнала 8000 выборок/с. Каждая речевая выборка квантуется на один из 256 уровней. Затем поток битов передается с использованием сигналов РСМ и принимается с нулевой межсимвольной интерференцией.

Решение

Процесс дискретизации и квантования дает слова РСМ, каждое из которых представляет одну выборку и относится к одному из L=256 различных уровней. Если каждая выборка передается как 256-уровневый импульс (символ) в кодировке РАМ, то из формулы (3.82) получим ширину полосы (без межсимвольной интерференции), требуемую для передачи символов/с.

Гц

Здесь равенство достигается только при использовании идеальной фильтрации Найквиста. Поскольку цифровая телефонная система использует (двоичные) сигналы РСМ, каждое слово РСМ преобразовывается в бит. Следовательно, полоса, необходимая для передачи речи с использованием РСМ, равна следующему выражению.

Описанный аналоговый канал передачи речи (3 кГц) обычно требует полосы порядка 4 кГц, включая некоторые разделительные полосы между каналами, называемые защитными (guard band). Следовательно, при использовании формата РСМ, 8-битового квантования и двоичной передачи с сигналами РСМ требуется примерно в 8 раз большая полоса, чем при использовании аналогового канала.

3.3.3. Демодуляция/обнаружение сформированных импульсов

3.3.3.1. Согласованные и обычные фильтры

Обычные фильтры отсекают нежелательные спектральные компоненты принятого сигнала при поддержании некоторой точности воспроизведения сигналов в выбранной области спектра, называемой полосой пропускания (pass-band). В общем случае эти фильтры разрабатываются для обеспечения приблизительно одинакового усиления, их характеристика дает линейное увеличение фазы в зависимости от частоты в пределах полосы пропускания и минимальное поглощение в остальной части спектра, именуемой полосой заграждения (stop-band). Согласованный фильтр имеет несколько иные «проектные приоритеты», направленные на максимизацию отношения SNR известного сигнала при шуме AWGN. В обычных фильтрах используются случайные сигналы, и результат фильтрации определяется только полосами сигналов, тогда как согласованные фильтры применяются с известными сигналами, имеющими произвольные параметры (такие, как амплитуда и время). Согласованный фильтр можно рассматривать как шаблон, который согласовывает обрабатываемый сигнал с известной формой. Обычный фильтр сохраняет временного или спектральную структуру сигнала. Согласованный фильтр, наоборот, в значительной степени модифицирует временную структуру путем сбора энергии сигнала, которая согласовывается с его шаблоном, и в завершение каждого интервала передачи символа представляет результат фильтрации в виде значения максимальной амплитуды. Вообще, в цифровой связи приемник обрабатывает поступающие сигналы с помощью фильтров обоих типов. Задачей обычного фильтра является изоляция и извлечение высокоточной аппроксимации сигнала с последующей передачей результата согласованному фильтру. Согласованный фильтр накапливает энергию принятого сигнала, и в момент взятия выборки на выход фильтра подается напряжение, пропорциональное этой энергии, после чего следует обнаружение и дальнейшая обработка сигнала.

3.3.3.2. Импульсы Найквиста

Рассмотрим последовательность информационных импульсов на входе передатчика и последовательность импульсов, получаемую на выходе согласованного фильтра с характеристикой типа приподнятого косинуса (перед дискретизацией). На рис. 3.21 переданные данные представлены импульсными сигналами, которые появляются в моменты времени . Фильтрование приводит к расширению входящих сигналов, а следовательно, к запаздыванию их во времени. Время поступления импульсов обозначим . Импульс, переданный в момент времени . поступает в приемник в момент времени . Хвост, предшествующий основному лепестку демодулированного импульса, называется его предтечей (precursor). Для реальной системы с заданным системным эталонным временем принцип причинности дает условие , а разность времен выражает задержку распространения в системе. В данном примере интервал времени от начала предтечи демодулированного импульса и до появления его главного лепестку или максимальной амплитуды равен 3T (утроенное время передачи импульса). Каждый выходящий импульс последовательности накладывается на другие импульсы; каждый импульс воздействует на основные лепестки трех предшествующих и трех последующих импульсов. В подобном случае, когда импульс фильтруется (формируется) так, что занимает более одного интервала передачи символа, определяется параметр, называемый временем поддержки (support time) импульса. Время поддержки - это количество интервалов передачи символа в течение длительности импульса. На рис. 3.21 время поддержки импульса равно 6 интервалам передачи символа (7 информационных точек с 6 интервалами между ними).

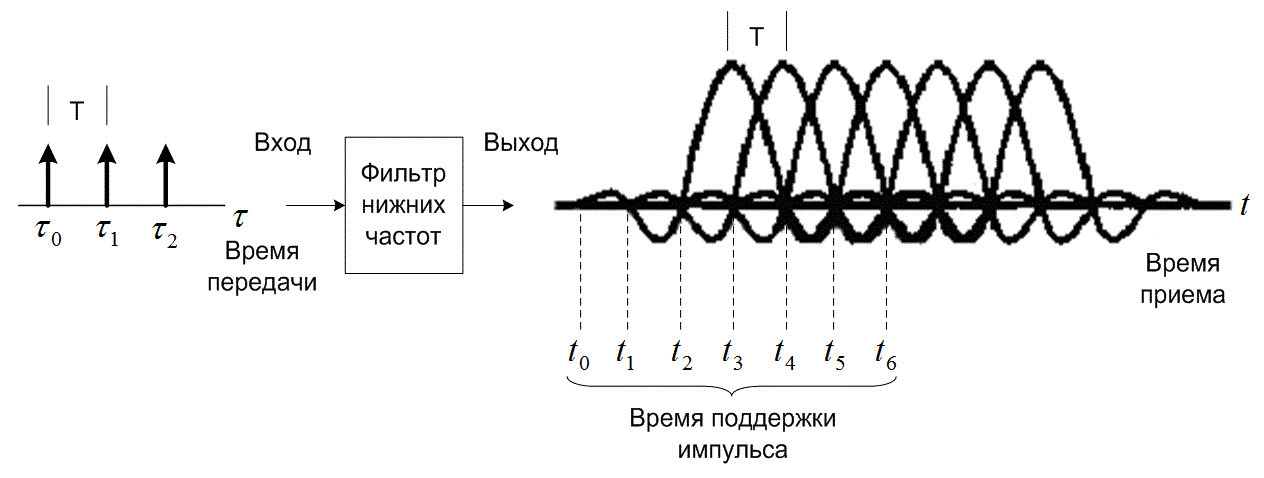
Рис. 3.21. Фильтрованная последовательность импульсов: выход и вход

На рис. 3.22, а показан импульсный отклик фильтра с характеристикой типа корня из приподнятого косинуса (максимальное значение нормированного фильтра равно единице, сглаживание фильтра ), а на рис. 3.22, б изображен импульсный отклик фильтра с характеристикой типа приподнятого косинуса, называемый импульсом Найквиста (нормирование и значение коэффициента сглаживания такие же, как и на рис. 3.22, а). Изучая эти два импульса, можно заметить, что они очень похожи. Однако первый имеет несколько более быстрые переходы, а значит, его спектр (корень квадратный из приподнятого косинуса) не так быстро затухает, как спектр (приподнятый косинус) импульса Найквиста. Еще одним малозаметным, но важным отличием является то, что импульс Найквиста с характеристикой типа корня из приподнятого косинуса не дает нулевой межсимвольной интерференции (можно проверить, что хвосты импульса на рис. 3.22, а не проходят через точку нулевой амплитуды в моменты взятия выборок). В то же время, если фильтр с характеристикой типа корня из приподнятого косинуса используется и в передатчике, и в приемнике, произведение передаточных функций двух фильтров дает характеристику типа приподнятого косинуса, что означает нулевую межсимвольную интерференцию на выходе.

Было бы неплохо рассмотреть, как импульсы Найквиста с характеристикой типа корня из приподнятого косинуса выглядят на выходе передатчика и какую форму они имеют после демодуляции на согласованном фильтре, характеристика которого также представляет собой корень из приподнятого косинуса.

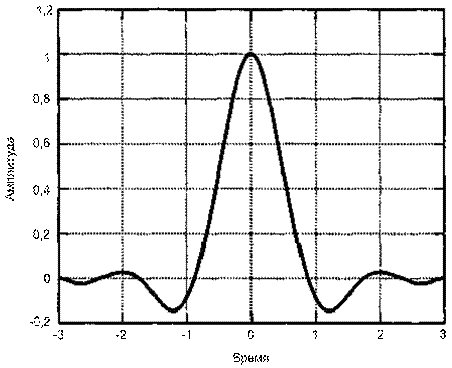
Рис. 3.22, а. Импульс Найквиста с характеристикой типа корня

из приподнятого косинуса

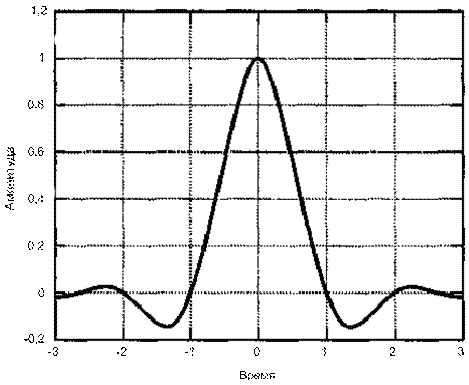
Рис. 3.22, б. Импульс Найквиста с характеристикой типа

приподнятого косинуса

На рис. 3.23, а в качестве примера передачи приведена последовательность символов сообщения из четверичного набора символов, где алфавит состоит из символов . Будем считать, что импульсы модулируются с помощью четверичной кодировки РАМ, а их форма определяется фильтром с характеристикой типа корня из приподнятого косинуса с коэффициентом сглаживания . Аналоговый сигнал на рис. 3.23, а описывает выход передатчика. Сигнал на выходе (последовательность импульсов Найквиста, форма которых получена с выхода фильтра с характеристикой типа корня из приподнятого косинуса) запаздывает относительно сигнала на входе (показанного в виде импульсов), но для удобства визуального представления, чтобы читатель мог сравнить выход фильтра с его входом, оба сигнала изображены как одновременные. В действительности передается (или модулируется) только аналоговый сигнал.

На рис. 3.23, б показаны те же задержанные символы сообщения, а также сигнал с выхода согласованного фильтра с характеристикой типа корня из приподнятого косинуса, что для всей системы в сумме дает передаточную функцию типа приподнятого косинуса.

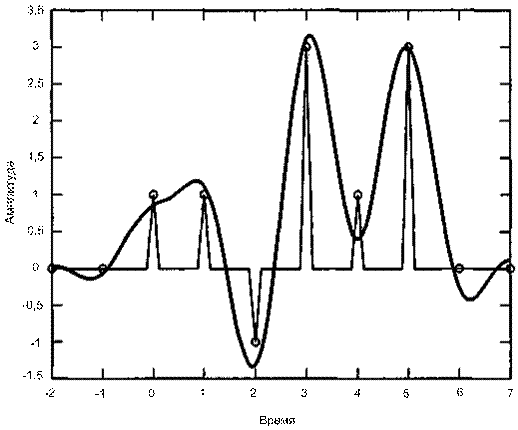
Рис. 3.23, а. М-уровневый сигнал Найквиста, пропущенный через фильтр с характеристикой типа корня из приподнятого косинуса, и входные дискретные значения, задержанные на некоторое время

Существует простой тест, позволяющий проверить, содержит ли фильтрованный сигнал с выхода межсимвольную интерференцию (предполагается отсутствие шума). Для этого требуется всего лишь произвести выборку фильтрованного сигнала в моменты времени, соответствующие исходным входящим выборкам; если полученные сигналы в результате выборки не отличаются от выборок исходного сообщения, то сигналы с выхода фильтра имеют нулевую межсимвольную интерференцию (в моменты взятия выборок). При сравнении рис. 3.23, а и 3.23, б на предмет межсимвольной интерференции видно, что дискретизация сигнала Найквиста на рис. 3.23, а (выход передатчика) не дает точных исходных выборок; в то же время дискретизация сигнала Найквиста на рис. 3.23, б (выход согласованного фильтра) дает точные исходные выборки. Это еще раз подтверждает, что фильтр Найквиста дает нулевую межсимвольную интерференцию в моменты взятия выборок, тогда как другие фильтры не имеют такой особенности.