Одной из мер качества аппроксимации является взвешенная среднеквадратическая ошибка.
![]() (13.76)
(13.76)
где В(Х) — это весовая матрица, а ХT— транспонированный вектор X. Минимизация может быть вычислительно проще, если весовая матрица является диагональной. Диагональная весовая матрица дает координатное множество с нарушенной связью (некоррелированное), так что ошибка минимизации вследствие квантования может находиться независимо по каждой координате.
Таким образом, преобразующее кодирование включает следующую последовательность операций, которые изображены на рис. 13.32.
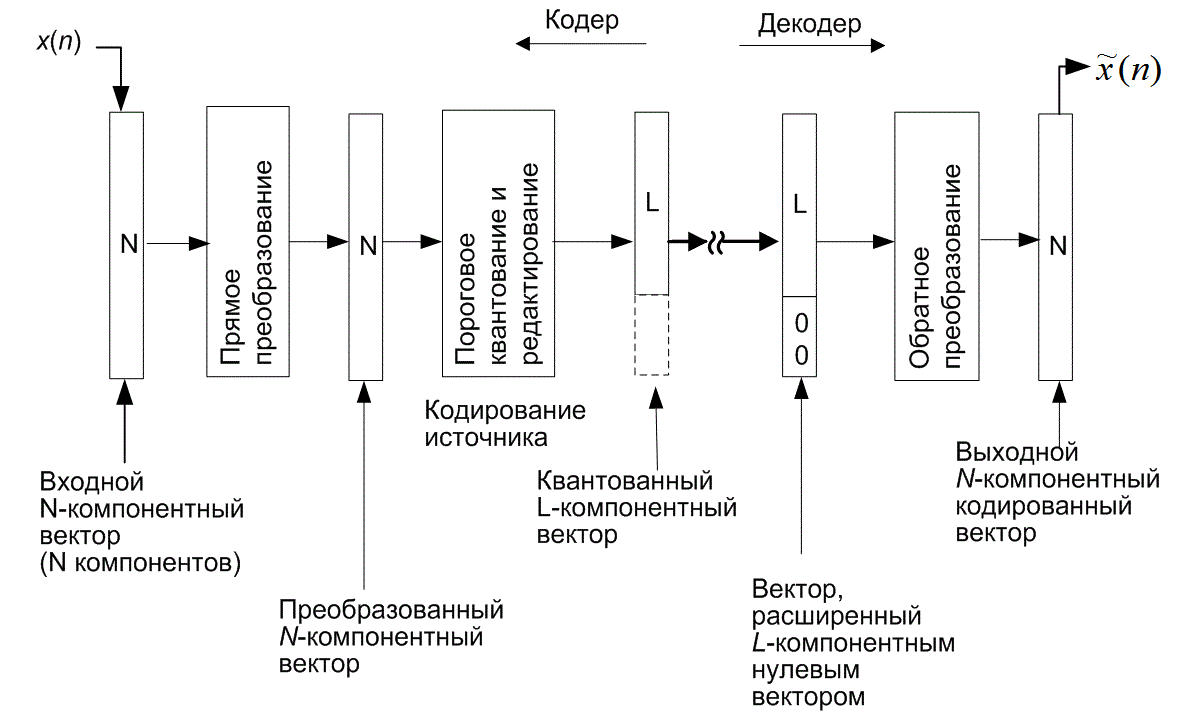
Рис. 13.32. Блочная диаграмма: преобразующее кодирование
1. К входному вектору применяется обратимое преобразование.
2. Коэффициенты преобразования квантуются.
3. Квантованные коэффициенты передаются и получаются.
4. Преобразование обращается с использованием квантованных коэффициентов.
Отметим, что при преобразовании не выполняется никакого кодирования источника; просто допускается более удобное описание вектора сигнала, которое позволяет легче использовать кодирование источника. Задача преобразования состоит в отображении коррелированной входной последовательности в другую систему координат, в которой координаты имеют меньшую корреляцию. Напомним, что это в точности представляет собой задачу, выполняемую кодером с предсказанием. Кодирование источника происходит посредством присвоения битового значения различным коэффициентам преобразования. Как часть этого присвоения, коэффициенты могут быть разделены на подмножества, которые квантуются с помощью различного числа бит, но не с помощью различных размеров шага квантования. Это присвоение отражает динамическую область (дисперсию) каждого коэффициента и может быть взвешено мерой, отражающей важность (относительно человеческого восприятия) элемента, переносимого каждым коэффициентом [17]. Например, подмножество коэффициентов может быть сведено к нулевой амплитуде или может быть квантовано с помощью 1 или 2 бит.
Преобразование может быть независимым от вектора данных. Примерами таких преобразований являются дискретное преобразование Фурье (discrete Fourier transform — DFT, ДПФ), дискретное преобразование Уолша-Адамара (discrete Walsh-Hadamar transform — DWHT), дискретное косинус-преобразование (discrete cosine transform — DCT, ДКП) и дискретное наклонное преобразование (discrete slant transform — DST). Преобразование может быть также получено из вектора данных, как это делается в дискретном преобразовании Карунена-Лоэва (discrete Karhunen-Loeve transform — DKLT), иногда называемом преобразованием основного компонента (principal component transform — РСТ) [18]. Независимые от данных преобразования являются самыми простыми в реализации, но они не так хороши, как информационно-зависимые. Зачастую вычислительная простота является достаточным оправданием для использования независящих от данных преобразований. При хорошем субоптимальном преобразовании потери эффективности кодирования незначительны (как правило, меньше 2 дБ), и обычно при демонстрации рабочих характеристик упоминается ухудшение качества.
13.6.1. Квантование для преобразующего кодирования
Преобразующие кодеры обычно называются спектральными, поскольку сигнал описывается через свое спектральное разложение (в выбранном базисном множестве). Спектральные члены вычисляются для неперекрывающихся последовательных блоков входных данных. Таким образом, выход преобразующего кодера может рассматриваться как множество временных рядов, один ряд для каждого спектрального члена. Дисперсия каждого ряда может быть определена, и каждый ряд может быть квантован с использованием разного числа бит. Допуская независимое квантование каждого коэффициента преобразования, имеем возможность распределения фиксированного числа бит среди коэффициентов преобразования для получения минимальной ошибки квантования.
13.6.2. Многополосное кодирование
Преобразующие кодеры в разделе 13.6 были описаны как выполняющие деление входного сигнала на множество медленно изменяющихся временных рядов, каждый из которых связан с определенным базисным вектором преобразования. Спектральные члены (скалярные произведения данных с базисными векторами) вычисляются с помощью множества скалярных произведений. Множество скалярных произведений может быть вычислено с помощью множества фильтров с конечной импульсной характеристикой [19]. С этой целью преобразующий кодер может рассматриваться как выполняющий разделение полосы частот входных данных на отдельные каналы. Обобщая, получим, что многополосный кодер, который выполняет спектральное разделение полосы частот на отдельные каналы с помощью набора непрерывных узкополосных фильтров, может рассматриваться в качестве частного случая преобразующего кодера. (Типичный многополосный кодер изображен на рис. 13.33.)
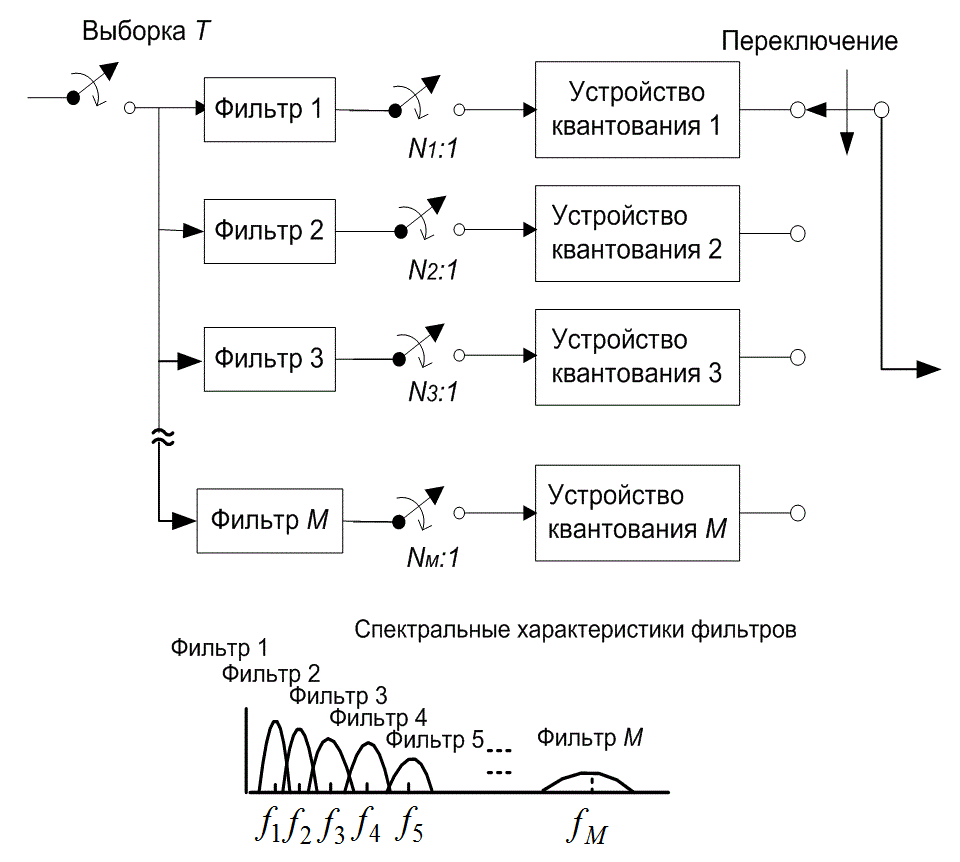
Рис. 13.33. Многополосное кодирование
Спектральное разложение данных (как и фильтрование) допускает различное формирование класса специальных базисных множеств (т.е. спектральных фильтров), в частности базисных множеств, которые отражают приемлемые предпочтения пользователя и модели источника. Например, шум квантования, сгенерированный в полосе частот с большой дисперсией, будет ограничен этой полосой частот; он не будет проникать в соседнюю полосу частот, имеющую низкую дисперсию и, следовательно, уязвимую для низкоуровневых сигналов, которые замаскированы шумом. Имеем также выбор формирующих фильтров с равными или неравными полосами частот (рис. 13.33). Таким образом, можно независимо каждой подполосе приписать выборочную частоту, соответствующую ее ширине полосы частот, и число бит квантования, соответствующее ее дисперсии. Для сравнения, в общепринятом преобразующем кодировании амплитуда каждого базисного вектора выбирается с одинаковой частотой.
Многополосный кодер может быть создан как трансмультиплексор (преобразователь вида уплотнения). Здесь входной сигнал рассматривается в виде составленного из множества базисных функций, моделированных как независимые подканалы узкой полосы частот. Кодер разделяет входной сигнал на множество каналов с низкой скоростью передачи данных, уплотненных с временным разделением (time-division multiplexing — TDM). После квантования и передачи декодер обращает процесс фильтрации и повторной выборки, преобразуя каналы TDM обратно в исходный сигнал. При классическом подходе к этому процессу можно использовать множество узкополосных фильтров с этапами смешивания, фильтрации нижних частот и дискретизации на пониженной частоте (часто называемой децимацией, или прореживанием). Эта операция фильтрации сокращает входную полосу частот до выбранной полосы частот канала и повторно выбирает сигнал до самой низкой частоты, что позволяет избежать наложения разделенных полос частот данных. В приемнике производится обратный процесс. Разделенные на полосы данные для увеличения их частоты до желаемой частоты дискретизации проходят через интерполирующие фильтры и смешиваются обратно до их соответствующего спектрального положения. Чтобы создать исходный смешанный сигнал, они объединяются. Для кодирования речи или, в более общем смысле, для сигналов, которые связаны с механическим резонансом, желательны группы фильтров с неравными центральными частотами и неравными полосами частот. Такие фильтры называются пропорциональными наборами фильтров. Эти фильтры имеют логарифмически расположенные центральные частоты и полосы частот, пропорциональные центральным частотам. При рассмотрении на логарифмической шкале такое пропорциональное размещение выглядит как равномерное расположение полос частот и отражает спектральные свойства многих физических акустических источников.

