3.1.1. Рост вероятности ошибки в системах связи
3.1.2. Демодуляция и обнаружение
3.1.3. Векторное представление сигналов и шума
3.1.3.2. Обобщенное преобразование Фурье
3.1.3.3. Представление белого шума через ортогональные сигналы
3.1.4. Важнейший параметр систем цифровой связи - отношение сигнал/шум
3.1.5. Почему отношение
- это естественный критерий качества
3.2. Обнаружение двоичных сигналов в гауссовом шуме
3.2.1. Критерий максимального правдоподобия приема сигналов
3.2.3. Реализация корреляции в согласованном фильтре
3.2.3.1. Сравнение свертки и корреляции
3.2.3.2. Дилемма в представлении упорядоченных во времени событий
3.2.4. Оптимизация вероятности ошибки
3.2.5. Вероятность возникновения ошибки при двоичной передаче сигналов
3.2.5.1. Униполярная передача сигналов
3.2.5.2. Биполярная передача сигналов
3.2.5.3. Использование базисных функций для описания передачи сигналов
3.3. Межсимвольная интерференция
3.3.1. Формирование импульсов с целью снижения ISI
3.3.1.2. Фильтр с характеристикой типа приподнятого косинуса
3.3.2. Факторы роста вероятности ошибки
3.3.3. Демодуляция/обнаружение сформированных импульсов
3.1. Сигналы и шум
3.1.1. Рост вероятности ошибки в системах связи
Задача детектора - максимально безошибочно угадать принятый сигнал, насколько это возможно при данном ухудшении качества сигнала в процессе передачи. Существует две причины роста вероятности ошибки. Первая - это последствия фильтрации в передатчике, канале и приемнике, рассмотренные в разделе 3.3. В этом разделе показано, что неидеальная передаточная функция системы приводит к «размыванию» символов, или межсимвольной интерференции (intersymbol interference - ISI).
Вторая причина роста вероятности ошибки - электрические помехи, порождаемые различными источниками, такими как галактика и атмосфера, импульсные помехи, комбинационные помехи, а также интерференция с сигналами от других источников. (Этот вопрос подробно рассмотрен в главе 5.) При надлежащих мерах предосторожности можно устранить большую часть помех и уменьшить последствия интерференции.
В то же время существуют помехи, устранить которые нельзя; это - помехи, вызываемые тепловым движением электронов в любой проводящей среде. Это движение порождает в усилителях и каналах связи тепловой шум, который аддитивно накладывается на сигнал. Использование квантовой механики позволило разработать хорошо известную статистику теплового шума [1].
Основная статистическая характеристика теплового шума заключается в том, что его амплитуды распределены по нормальному или гауссову закону распределения, рассмотренному в разделе 1.5.5 (рис. 1.7). На этом рисунке показано, что наиболее вероятные амплитуды шума - амплитуды с небольшими положительными или отрицательными значениями. Теоретически шум может быть бесконечно большим, но на практике очень большие амплитуды шума крайне редки. Основная спектральная характеристика теплового шума в системе связи заключается в том, что его двусторонняя спектральная плотность мощности ![]() является плоской для всех частот, представляющих практический интерес. Другими словами, в тепловом шуме в среднем на низкочастотные флуктуации приходится столько же мощности на герц, сколько и на высокочастотные флуктуации - вплоть до частоты порядка
является плоской для всех частот, представляющих практический интерес. Другими словами, в тепловом шуме в среднем на низкочастотные флуктуации приходится столько же мощности на герц, сколько и на высокочастотные флуктуации - вплоть до частоты порядка ![]() герц. Если мощность шума характеризуется постоянной спектральной плотностью мощности, шум называется белым. Поскольку тепловой шум присутствует во всех системах связи и для многих систем является доминирующим источником помех, характеристики теплового шума часто используются для моделирования шума при обнаружении и проектировании приемников. Всякий раз, когда канал связи определен как канал AWGN (при отсутствии указаний на другие параметры, ухудшающие качество передачи), мы, по сути, говорим, что ухудшение качества сигнала связано исключительно с неустранимым тепловым шумом.
герц. Если мощность шума характеризуется постоянной спектральной плотностью мощности, шум называется белым. Поскольку тепловой шум присутствует во всех системах связи и для многих систем является доминирующим источником помех, характеристики теплового шума часто используются для моделирования шума при обнаружении и проектировании приемников. Всякий раз, когда канал связи определен как канал AWGN (при отсутствии указаний на другие параметры, ухудшающие качество передачи), мы, по сути, говорим, что ухудшение качества сигнала связано исключительно с неустранимым тепловым шумом.
3.1.2. Демодуляция и обнаружение
В течение данного интервала передачи сигнала, Т, бинарная узкополосная система передает один из двух возможных сигналов, обозначаемых как ![]() и
и ![]() . Подобным образом бинарная полосовая система передает один из двух возможных сигналов, обозначаемых как
. Подобным образом бинарная полосовая система передает один из двух возможных сигналов, обозначаемых как ![]() и
и ![]() . Поскольку общая трактовка демодуляции и обнаружения, по сути, совпадает для узкополосных и полосовых систем, будем использовать запись
. Поскольку общая трактовка демодуляции и обнаружения, по сути, совпадает для узкополосных и полосовых систем, будем использовать запись ![]() для обозначения передаваемого сигнала, вне зависимости от того, является система узкополосной или полосовой. Это позволяет совместить многие аспекты демодуляции/обнаружения в узкополосных системах, рассмотренные в данной главе, с соответствующими описаниями для полосовых систем, рассмотренных в главе 4. Итак, для любого канала двоичный сигнал, переданный в течение интервала
для обозначения передаваемого сигнала, вне зависимости от того, является система узкополосной или полосовой. Это позволяет совместить многие аспекты демодуляции/обнаружения в узкополосных системах, рассмотренные в данной главе, с соответствующими описаниями для полосовых систем, рассмотренных в главе 4. Итак, для любого канала двоичный сигнал, переданный в течение интервала ![]() , представляется следующим образом.
, представляется следующим образом.
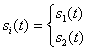
![]()
![]()
![]()
![]()
Принятый сигнал ![]() искажается вследствие воздействия шума
искажается вследствие воздействия шума ![]() и, возможно, неидеальной импульсной характеристики канала
и, возможно, неидеальной импульсной характеристики канала ![]() и описывается следующей формулой (1.1).
и описывается следующей формулой (1.1).
![]() (3.1)
(3.1)
В нашем случае ![]() предполагается процессом AWGN с нулевым средним, а знак «*» обозначает операцию свертки. Для бинарной передачи по идеальному, свободному от искажений каналу, где свертка с функцией
предполагается процессом AWGN с нулевым средним, а знак «*» обозначает операцию свертки. Для бинарной передачи по идеальному, свободному от искажений каналу, где свертка с функцией ![]() не ухудшает качество сигнала (поскольку для идеального случая
не ухудшает качество сигнала (поскольку для идеального случая ![]() - импульсная функция), вид
- импульсная функция), вид ![]() можно упростить.
можно упростить.
![]()
![]()
![]() (3.2)
(3.2)
Типичные функции демодуляции и обнаружения цифрового приемника показаны на рис. 3.1. Некоторые авторы используют термины «демодуляция» и «обнаружение» как синонимы. Демодуляцию (demodulation) мы определим как восстановление сигнала (в неискаженный узкополосный импульс), а обнаружение (detection) - как процесс принятия решения относительно цифрового значения этого сигнала. При отсутствии кодов коррекции ошибок на выход детектора поступают аппроксимации символов (или битов) сообщений ![]() (также называемые жестким решением). При использовании кодов коррекции ошибок на выход детектора поступают аппроксимации канальных символов (или кодированных битов) и
(также называемые жестким решением). При использовании кодов коррекции ошибок на выход детектора поступают аппроксимации канальных символов (или кодированных битов) и ![]() имеющие вид жесткого или мягкого решения (см. раздел 7.3.2). Для краткости термин «обнаружение» иногда применяется для обозначения совокупности всех этапов обработки сигнала, выполняемых в приемнике, вплоть до этапа принятия решения. Блок преобразования с понижением частоты, показанный на рис. 3.1 в разделе демодуляции, отвечает за трансляцию полосовых сигналов, работающих на определенных радиочастотах. Эта функция может реализовываться различными способами. Она может выполняться на входе приемника, в демодуляторе, распределяться между этими двумя устройствами или вообще не реализовываться.
имеющие вид жесткого или мягкого решения (см. раздел 7.3.2). Для краткости термин «обнаружение» иногда применяется для обозначения совокупности всех этапов обработки сигнала, выполняемых в приемнике, вплоть до этапа принятия решения. Блок преобразования с понижением частоты, показанный на рис. 3.1 в разделе демодуляции, отвечает за трансляцию полосовых сигналов, работающих на определенных радиочастотах. Эта функция может реализовываться различными способами. Она может выполняться на входе приемника, в демодуляторе, распределяться между этими двумя устройствами или вообще не реализовываться.
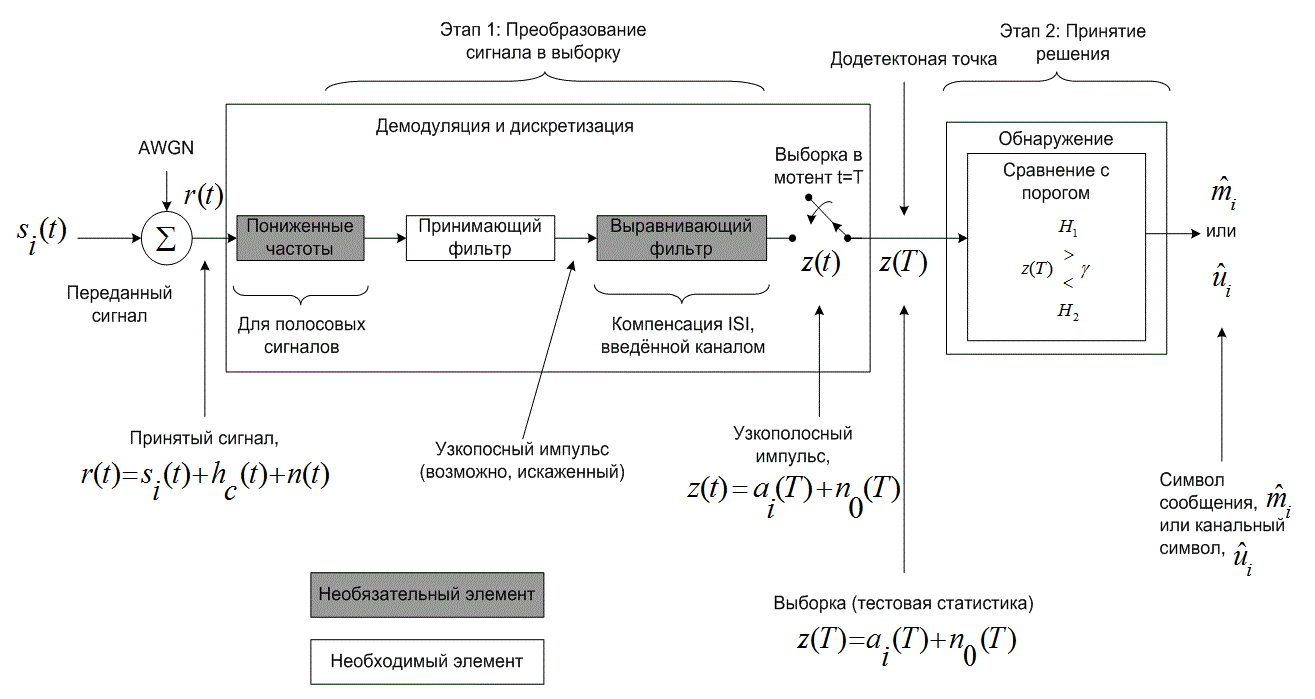
Рис.3.1. Два основных этапа в процессе демодуляции/ обнаружения цифровых сигналов
В блоке демодуляции и дискретизации (рис. 3.1) изображен принимающий фильтр (по сути, демодулятор), выполняющий восстановление сигнала в качестве подготовки к следующему необходимому этапу - обнаружению. Фильтрация в передатчике и канале обычно приводит к искажению принятой последовательности импульсов, вызванному межсимвольной интерференцией, а значит, эти импульсы не совсем готовы к дискретизации и обнаружению. Задачей принимающего фильтра является восстановление узкополосного импульса с максимально возможным отношением сигнал/шум (signal-to-noise ratio - SNR) и без межсимвольной интерференции. Оптимальный принимающий фильтр, выполняющий такую задачу, называется согласованным (matched), или коррелятором (correlator) и описывается в разделах 3.2.2 и 3.2.3. За принимающим фильтром может находиться выравнивающий фильтр (equalizing filter), или эквалайзер (equalizer); он необходим только в тех системах, в которых сигнал может искажаться вследствие межсимвольной интерференции, введенной каналом. Принимающий и выравнивающий фильтры показаны как два отдельных блока, что подчеркивает различие их функций. Впрочем, в большинстве случаев при использовании эквалайзера для выполнения обеих функций (а следовательно, и для компенсации искажения, внесенного передатчиком и каналом) может разрабатываться единый фильтр. Такой составной фильтр иногда называется просто выравнивающим или принимающим и выравнивающим.
На рис. 3.1 выделены два этапа процесса демодуляции/обнаружения. Этап 1, преобразование сигнала в выборку, выполняется демодулятором и следующим за ним устройством дискретизации. В конце каждого интервала передачи символа Т на выход устройства дискретизации, додетекторную точку, поступает выборка ![]() , иногда называемая тестовой статистикой. Значение напряжения выборки
, иногда называемая тестовой статистикой. Значение напряжения выборки ![]() прямо пропорционально энергии принятого символа и обратно пропорционально шуму. На этапе 2 принимается решение относительно цифрового значения выборки (выполняется обнаружение). Предполагается, что шум является случайным гауссовым процессом, а принимающий фильтр демодулятора - линейным. Линейная операция со случайным гауссовым процессом дает другой случайный гауссов процесс [2]. Следовательно, на выходе фильтра шум также является гауссовым. Значит, выход этапа 1 можно описать выражением
прямо пропорционально энергии принятого символа и обратно пропорционально шуму. На этапе 2 принимается решение относительно цифрового значения выборки (выполняется обнаружение). Предполагается, что шум является случайным гауссовым процессом, а принимающий фильтр демодулятора - линейным. Линейная операция со случайным гауссовым процессом дает другой случайный гауссов процесс [2]. Следовательно, на выходе фильтра шум также является гауссовым. Значит, выход этапа 1 можно описать выражением
![]()
![]() (3.3)
(3.3)
где ![]() - желаемый компонент сигнала, а
- желаемый компонент сигнала, а ![]() - шум. Для упрощения записи выражение (3.3) будем иногда представлять в виде
- шум. Для упрощения записи выражение (3.3) будем иногда представлять в виде ![]() . Шумовой компонент
. Шумовой компонент ![]() - это случайная гауссова переменная с нулевым средним, поэтому
- это случайная гауссова переменная с нулевым средним, поэтому ![]() - случайная гауссова переменная со средним
- случайная гауссова переменная со средним ![]() или
или ![]() , в зависимости от того, передавался двоичный нуль или двоичная единица. Как описывалось в разделе 1.5.5, плотность вероятности случайного гауссового шума
, в зависимости от того, передавался двоичный нуль или двоичная единица. Как описывалось в разделе 1.5.5, плотность вероятности случайного гауссового шума ![]() можно выразить как
можно выразить как
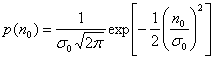 , (3.4)
, (3.4)
где ![]() - дисперсия шума. Используя выражения (3.3) и (3.4), можно выразить плотности условных вероятностей
- дисперсия шума. Используя выражения (3.3) и (3.4), можно выразить плотности условных вероятностей ![]() и
и ![]() .
.
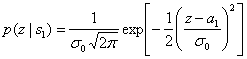 (3.5)
(3.5)
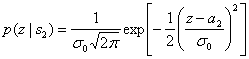 (3.6)
(3.6)
Эти плотности условных вероятностей показаны на рис. 3.2. Плотность ![]() , изображенная справа, называется правдоподобием
, изображенная справа, называется правдоподобием ![]() и показывает плотность вероятности случайной переменной
и показывает плотность вероятности случайной переменной ![]() при условии передачи символа
при условии передачи символа ![]() . Подобным образом функция
. Подобным образом функция ![]() (слева) является правдоподобием
(слева) является правдоподобием ![]() и показывает плотность вероятности
и показывает плотность вероятности ![]() при условии передачи символа
при условии передачи символа ![]() . Ось абсцисс,
. Ось абсцисс, ![]() , представляет полный диапазон возможных значений выборки, взятой в течение этапа 1, изображенного на рис. 3.1.
, представляет полный диапазон возможных значений выборки, взятой в течение этапа 1, изображенного на рис. 3.1.
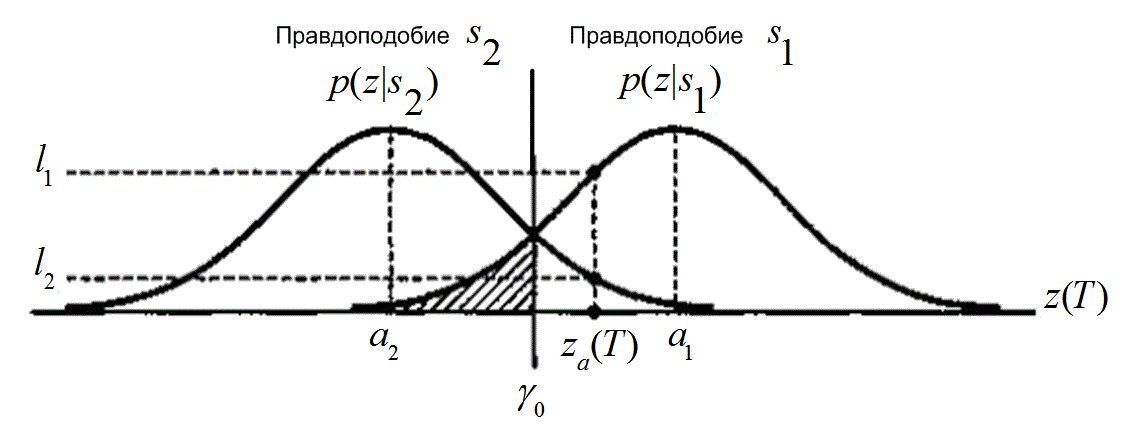
Рис.3.2. Плотности условных вероятностей: ![]() и
и ![]()
После того как принятый сигнал преобразован в выборку, действительная форма сигнала уже не имеет значения; сигналы всех типов, преобразованные в одинаковое значение ![]() , идентичны для схемы обнаружения. Далее будет показано, что оптимальный принимающий фильтр (согласованный фильтр) на этапе 1 (рис. 3.1) отображает все сигналы с равными энергиями в одну и ту же точку
, идентичны для схемы обнаружения. Далее будет показано, что оптимальный принимающий фильтр (согласованный фильтр) на этапе 1 (рис. 3.1) отображает все сигналы с равными энергиями в одну и ту же точку ![]() . Следовательно, важным параметром процесса обнаружения является энергия (а не форма) принятого сигнала, именно поэтому анализ обнаружения для узкополосных сигналов не отличается от анализа для полосовых сигналов. Поскольку
. Следовательно, важным параметром процесса обнаружения является энергия (а не форма) принятого сигнала, именно поэтому анализ обнаружения для узкополосных сигналов не отличается от анализа для полосовых сигналов. Поскольку ![]() является сигналом напряжения, пропорциональным энергии принятого символа, то чем больше амплитуда
является сигналом напряжения, пропорциональным энергии принятого символа, то чем больше амплитуда ![]() , тем более достоверным будет процесс принятия решения относительно цифрового значения сигнала. На этапе 2 обнаружение выполняется посредством выбора гипотезы, являющейся следствием порогового измерения
, тем более достоверным будет процесс принятия решения относительно цифрового значения сигнала. На этапе 2 обнаружение выполняется посредством выбора гипотезы, являющейся следствием порогового измерения
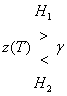 , (3.7)
, (3.7)
где ![]() и
и ![]() - две возможные (бинарные) гипотезы. Приведенная запись указывает, что гипотеза
- две возможные (бинарные) гипотезы. Приведенная запись указывает, что гипотеза ![]() выбирается при
выбирается при ![]() , а
, а ![]() - при
- при ![]() . Если
. Если ![]() , решение может быть любым. Выбор
, решение может быть любым. Выбор ![]() , равносилен тому, что передан был сигнал
, равносилен тому, что передан был сигнал ![]() , а значит, результатом обнаружения является двоичная единица. Подобным образом выбор
, а значит, результатом обнаружения является двоичная единица. Подобным образом выбор ![]() равносилен передаче сигнала
равносилен передаче сигнала ![]() , а значит, результатом обнаружения является двоичный нуль.
, а значит, результатом обнаружения является двоичный нуль.
3.1.3. Векторное представление сигналов и шума
Рассмотрим геометрическое или векторное представление, приемлемое как для узкополосных, так и полосовых сигналов. Определим N-мерное ортогональное пространство как пространство, определяемое набором N линейно независимых функций ![]() , именуемых базисными. Любая функция этого пространства может выражаться через линейную комбинацию базисных функций, которые должны удовлетворять условию
, именуемых базисными. Любая функция этого пространства может выражаться через линейную комбинацию базисных функций, которые должны удовлетворять условию
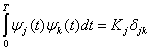
![]()
![]() (3.8, а)
(3.8, а)
где оператор
![]()
![]()
![]() (3.8, б)
(3.8, б)
называется дельта-функцией Кронекера и определяется формулой (3.8,б). При ненулевых константах ![]() пространство именуется ортогональным. Если базисные функции нормированы так, что все
пространство именуется ортогональным. Если базисные функции нормированы так, что все ![]() , пространство называется ортонормированным. Основное условие ортогональности можно сформулировать следующим образом: каждая функция
, пространство называется ортонормированным. Основное условие ортогональности можно сформулировать следующим образом: каждая функция ![]() набора базисных функций должна быть независимой от остальных функций набора. Каждая функция
набора базисных функций должна быть независимой от остальных функций набора. Каждая функция ![]() не должна интерферировать с другими функциями в процессе обнаружения. С геометрической точки зрения все функции
не должна интерферировать с другими функциями в процессе обнаружения. С геометрической точки зрения все функции ![]() взаимно перпендикулярны. Пример подобного пространства с N=3 показан на рис. 3.3, где взаимно перпендикулярные оси обозначены
взаимно перпендикулярны. Пример подобного пространства с N=3 показан на рис. 3.3, где взаимно перпендикулярные оси обозначены ![]() ,
, ![]() и
и ![]() . Если
. Если ![]() соответствует действительному компоненту напряжения или тока сигнала, нормированному на сопротивление 1 Ом, то, используя формулы (1.5) и (3.8), получаем следующее выражение для нормированной энергии в джоулях,
соответствует действительному компоненту напряжения или тока сигнала, нормированному на сопротивление 1 Ом, то, используя формулы (1.5) и (3.8), получаем следующее выражение для нормированной энергии в джоулях,
переносимой сигналом ![]() за Т секунд.
за Т секунд.
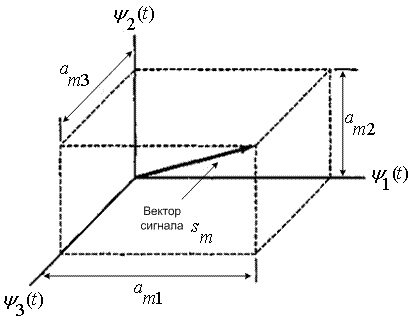
Рис. 3.3. Векторное представление сигнала ![]()
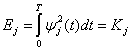 (3.9)
(3.9)
Одной из причин нашего внимания к ортогональному сигнальному пространству является то, что в нем проще всего определяется Евклидова мера расстояния, используемая в процессе обнаружения. Стоит отметить, что даже если волны, переносящие сигналы, не формируют подобного пространства, они могут преобразовываться в линейную комбинацию ортогональных сигналов. Можно показать [3], что произвольный конечный набор сигналов ![]()
![]() , где каждый элемент множества физически реализуем и имеет длительность Т, можно выразить как линейную комбинацию N ортогональных сигналов
, где каждый элемент множества физически реализуем и имеет длительность Т, можно выразить как линейную комбинацию N ортогональных сигналов ![]() ,
, ![]() ,...,
,..., ![]() , где
, где ![]() , так, что
, так, что
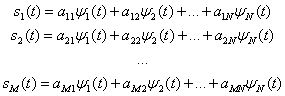
Эти соотношения можно записать в более компактной форме.
![]()
![]() (3.10)
(3.10)
![]() ,
,
где
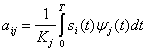
![]()
![]()
![]() (3.11)
(3.11)
![]() - это коэффициент при
- это коэффициент при ![]() разложения сигнала
разложения сигнала ![]() по базисным функциям. Вид базиса
по базисным функциям. Вид базиса ![]() не задается; эти сигналы выбираются с точки зрения удобства и зависят от формы волн передачи сигналов. Набор таких волн
не задается; эти сигналы выбираются с точки зрения удобства и зависят от формы волн передачи сигналов. Набор таких волн ![]() можно рассматривать как набор векторов
можно рассматривать как набор векторов ![]() . Если, например, N=3, то сигналу
. Если, например, N=3, то сигналу
![]() ,
,
соответствует вектор ![]() , который можно изобразить как точку в трехмерном Евклидовом пространстве с координатами
, который можно изобразить как точку в трехмерном Евклидовом пространстве с координатами ![]() , как показано на рис. 3.3. Взаимная ориентация векторов сигналов описывает связь между сигналами (относительно их фаз или частот), а амплитуда каждого вектора набора
, как показано на рис. 3.3. Взаимная ориентация векторов сигналов описывает связь между сигналами (относительно их фаз или частот), а амплитуда каждого вектора набора ![]() является мерой энергии сигнала, перенесенной в течение времени передачи символа. Вообще, после выбора набора из N ортогональных функций, каждый из переданных сигналов
является мерой энергии сигнала, перенесенной в течение времени передачи символа. Вообще, после выбора набора из N ортогональных функций, каждый из переданных сигналов ![]() полностью определяется вектором его коэффициентов.
полностью определяется вектором его коэффициентов.
![]()
![]() (3.12)
(3.12)
В дальнейшем для отображения сигналов в векторной форме будем использовать запись ![]() или
или ![]() . На рис. 3.4 в векторной форме (которая в данном случае является очень удобной) показан процесс обнаружения. Векторы
. На рис. 3.4 в векторной форме (которая в данном случае является очень удобной) показан процесс обнаружения. Векторы ![]() и
и ![]() представляют сигналы-прототипы, или опорные сигналы, принадлежащие набору из М сигналов,
представляют сигналы-прототипы, или опорные сигналы, принадлежащие набору из М сигналов, ![]() . Приемник априори знает местонахождение в пространстве сигналов всех векторов-прототипов, принадлежащих М-мерному множеству. В процессе передачи каждый сигнал подвергается воздействию шумов, так что в действительности принимается искаженная версия исходного сигнала (например,
. Приемник априори знает местонахождение в пространстве сигналов всех векторов-прототипов, принадлежащих М-мерному множеству. В процессе передачи каждый сигнал подвергается воздействию шумов, так что в действительности принимается искаженная версия исходного сигнала (например, ![]() или
или ![]() ), где
), где ![]() - вектор помех. Будем считать, что помехи являются аддитивными и имеют гауссово распределение; следовательно, результирующее распределение возможных принимаемых сигналов - это кластер или облако точек вокруг
- вектор помех. Будем считать, что помехи являются аддитивными и имеют гауссово распределение; следовательно, результирующее распределение возможных принимаемых сигналов - это кластер или облако точек вокруг ![]() и
и ![]() . Кластер сгущается к центру и разрежается с увеличением расстояния от прототипа. Стрелочка с пометкой «
. Кластер сгущается к центру и разрежается с увеличением расстояния от прототипа. Стрелочка с пометкой «![]() » представляет вектор сигнала, который поступает в приемник в течение определенного интервала передачи символа. Задача приемника - определить, на какой из прототипов М-мерного множества сигнал «похож» больше. Мерой «сходства» может быть расстояние. Приемник или детектор должен решить, какой из прототипов сигнального пространства ближе к принятому вектору
» представляет вектор сигнала, который поступает в приемник в течение определенного интервала передачи символа. Задача приемника - определить, на какой из прототипов М-мерного множества сигнал «похож» больше. Мерой «сходства» может быть расстояние. Приемник или детектор должен решить, какой из прототипов сигнального пространства ближе к принятому вектору ![]() . Анализ всех схем демодуляции или обнаружения включает использование понятия расстояние между принятым сигналом и набором возможных переданных сигналов. Детектор должен следовать одному простому правилу: определять
. Анализ всех схем демодуляции или обнаружения включает использование понятия расстояние между принятым сигналом и набором возможных переданных сигналов. Детектор должен следовать одному простому правилу: определять ![]() к тому же классу, к которому принадлежит его ближайший сосед (ближайший вектор-прототип).
к тому же классу, к которому принадлежит его ближайший сосед (ближайший вектор-прототип).
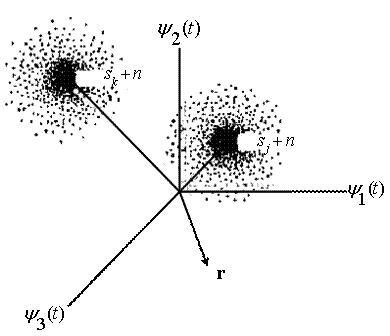
Рис.3.4. Сигналы и шум в трехмерном векторном пространстве
3.1.3.1. Энергия сигнала
С помощью формул (1.5), (3.10) и (3.8) нормированную энергию ![]() , связанную с сигналом
, связанную с сигналом ![]() в течение периода передачи символа Т, можно выразить через ортогональные компоненты
в течение периода передачи символа Т, можно выразить через ортогональные компоненты ![]() .
.
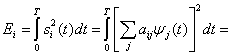 (3.13)
(3.13)
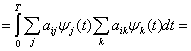 (3.14)
(3.14)
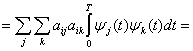 (3.15)
(3.15)
![]() (3.16)
(3.16)
![]()
![]() (3.17)
(3.17)
Уравнение (3.17) - это частный случай теоремы Парсеваля, связывающей интеграл от квадрата сигнала ![]() с суммой квадратов коэффициентов ортогонального разложения
с суммой квадратов коэффициентов ортогонального разложения ![]() . При использовании ортонормированных функций (т.е. при
. При использовании ортонормированных функций (т.е. при ![]() ) нормированная энергия за промежуток времени Т дается следующим выражением.
) нормированная энергия за промежуток времени Т дается следующим выражением.
![]() (3.18)
(3.18)
Если все сигналы ![]() имеют одинаковую энергию, формулу (3.18) можно записать следующим образом.
имеют одинаковую энергию, формулу (3.18) можно записать следующим образом.
3.1.3.2. Обобщенное преобразование Фурье
Преобразование, описанное формулами (3.8), (3.10) и (3.11), называется обобщенным преобразованием Фурье. При обычном преобразовании Фурье множество ![]() включает синусоиды и косинусоиды, а в случае обобщенного преобразования оно не ограничено какой-либо конкретной формой; это множество должно лишь удовлетворять условию ортогональности, записанному в форме уравнения (3.8). Обобщенное преобразование Фурье позволяет представить любой произвольный интегрируемый набор сигналов (или шумов) в виде линейной комбинации ортогональных сигналов [3]. Следовательно, в подобном ортогональном пространстве в качестве критерия принятия решения для обнаружения любого набора сигналов при шуме AWGN вполне оправдано использование расстояния (Евклидового расстояния). Вообще, важнейшее применение этого ортогонального преобразования связано с действительной передачей и приемом сигналов. Передача неортогонального набора сигналов в общем случае осуществляется посредством подходящего взвешивания ортогональных компонентов несущих.
включает синусоиды и косинусоиды, а в случае обобщенного преобразования оно не ограничено какой-либо конкретной формой; это множество должно лишь удовлетворять условию ортогональности, записанному в форме уравнения (3.8). Обобщенное преобразование Фурье позволяет представить любой произвольный интегрируемый набор сигналов (или шумов) в виде линейной комбинации ортогональных сигналов [3]. Следовательно, в подобном ортогональном пространстве в качестве критерия принятия решения для обнаружения любого набора сигналов при шуме AWGN вполне оправдано использование расстояния (Евклидового расстояния). Вообще, важнейшее применение этого ортогонального преобразования связано с действительной передачей и приемом сигналов. Передача неортогонального набора сигналов в общем случае осуществляется посредством подходящего взвешивания ортогональных компонентов несущих.
Пример 3.1. Ортогональное представление сигналов
На рис. 3.5 иллюстрируется утверждение, что любой произвольный интегрируемый набор сигналов может представляться как линейная комбинация ортогональных сигналов. На рис. 3.5, а показан набор из трех сигналов, ![]() ,
, ![]() и
и ![]() .
.
а) Покажите, что данные сигналы не взаимно ортогональны.
б) На рис. 3.5, б показаны два сигнала ![]() и
и ![]() . Докажите, что эти сигналы ортогональны.
. Докажите, что эти сигналы ортогональны.
в) Покажите, как неортогональные сигналы из п. а можно выразить как линейную комбинацию ортогональных сигналов из п. б.
г) На рис. 3.5, в показаны другие два сигнала ![]() и
и ![]() . Покажите, как неортогональные сигналы, показанные на рис. 3.5, а, выражаются через линейную комбинацию сигналов, изображенных на рис. 3.5, в.
. Покажите, как неортогональные сигналы, показанные на рис. 3.5, а, выражаются через линейную комбинацию сигналов, изображенных на рис. 3.5, в.
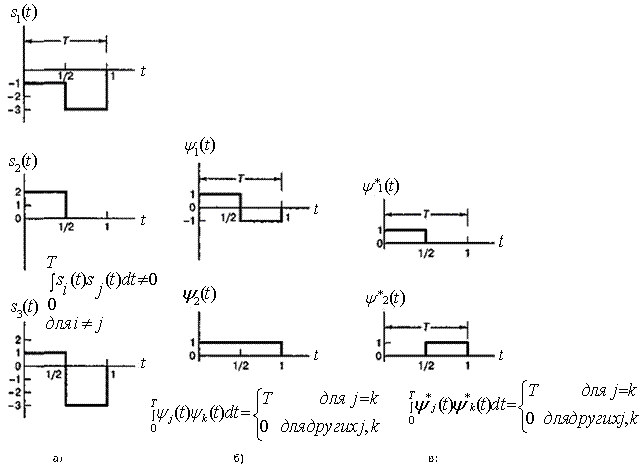
Рис. 3.5. Пример выражения произвольного набора сигналов через ортогональный набор: а) произвольный набор сигналов;
б) набор ортогональных базисных функций;
в) другой набор ортогональных базисных функций
Решение
а) Сигналы ![]() ,
, ![]() и
и ![]() , очевидно, не являются взаимно ортогональными, поскольку не удовлетворяют требованиям, указанным в формуле (3.8), т.е. интегрирование по времени (по периоду передачи символа) скалярного произведения любых двух из трех сигналов не равно нулю. Покажем это для сигналов
, очевидно, не являются взаимно ортогональными, поскольку не удовлетворяют требованиям, указанным в формуле (3.8), т.е. интегрирование по времени (по периоду передачи символа) скалярного произведения любых двух из трех сигналов не равно нулю. Покажем это для сигналов ![]() и
и ![]() .
.
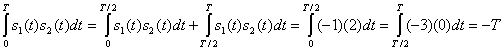
Подобным образом интегрирование по интервалу времени Т каждого из скалярных произведений ![]()
![]() и
и ![]()
![]() дает ненулевой результат. Следовательно, множество сигналов
дает ненулевой результат. Следовательно, множество сигналов ![]()
![]() на рис. 3.5, а не является ортогональным
на рис. 3.5, а не является ортогональным
б) Используя формулу (3.8), докажем, что ![]() и
и ![]() ортогональны.
ортогональны.
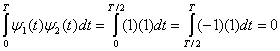
в) С использованием формулы (3.11) при ![]() , неортогональное множество сигналов
, неортогональное множество сигналов ![]()
![]() можно выразить через линейную комбинацию ортогональных базисных сигналов
можно выразить через линейную комбинацию ортогональных базисных сигналов ![]()
![]() .
.
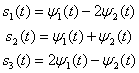
г) Подобно тому, как было сделано в п. в, неортогональное множество ![]()
![]() можно выразить через ортогональный набор базисных функций
можно выразить через ортогональный набор базисных функций ![]()
![]() , изображенный на рис. 3.5, в.
, изображенный на рис. 3.5, в.
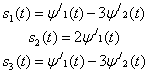
Эти соотношения показывают, как произвольный набор сигналов ![]() выражается через линейную комбинацию сигналов ортогонального набора
выражается через линейную комбинацию сигналов ортогонального набора ![]() , что описывается формулами (3.10) и (3.11). Какое практическое значение имеет возможность представления сигналов
, что описывается формулами (3.10) и (3.11). Какое практическое значение имеет возможность представления сигналов ![]()
![]() и
и ![]() через сигналы
через сигналы ![]() ,
, ![]() и соответствующие коэффициенты? Если мы хотим, чтобы система передавала сигналы
и соответствующие коэффициенты? Если мы хотим, чтобы система передавала сигналы ![]() ,
, ![]() и
и ![]() , достаточно, чтобы передатчик и приемник реализовывались только с использованием двух базисных функций
, достаточно, чтобы передатчик и приемник реализовывались только с использованием двух базисных функций ![]() и
и ![]() , а не трех исходных сигналов. Получить ортогональный набор базисных функций
, а не трех исходных сигналов. Получить ортогональный набор базисных функций ![]() из любого данного набора сигналов
из любого данного набора сигналов ![]() позволяет процесс ортогонализации Грамма-Шмидта. (Подробно этот процесс описан в приложении 4А работы [4].) .
позволяет процесс ортогонализации Грамма-Шмидта. (Подробно этот процесс описан в приложении 4А работы [4].) .
3.1.3.3. Представление белого шума через ортогональные сигналы
Аддитивный белый гауссов шум (additive white Gaussian noise - AWGN), как и любой другой сигнал, можно выразить как линейную комбинацию ортогональных сигналов. Для последующего рассмотрения процесса обнаружения сигналов шум удобно разделить на два компонента:
![]() , (3.20)
, (3.20)
где
![]() (3.21)
(3.21)
является шумом в пространстве сигналов или проекцией компонентов шума на координаты сигнала ![]() , a
, a
![]() (3.22)
(3.22)
есть шумом вне пространства сигналов. Другими словами, ![]() можно рассматривать как шум, эффективно отсеиваемый детектором, a
можно рассматривать как шум, эффективно отсеиваемый детектором, a ![]() - как шум, который будет «вмешиваться» в процесс обнаружения. Итак, сигнал шума
- как шум, который будет «вмешиваться» в процесс обнаружения. Итак, сигнал шума ![]() можно выразить следующим образом.
можно выразить следующим образом.
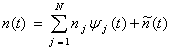 (3.23)
(3.23)
где
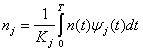 для всех
для всех ![]() (3.24)
(3.24)
и
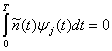 для всех
для всех ![]() (3.25)
(3.25)
Компонент ![]() шума, выраженный в формуле (3.21), следовательно, можно считать просто равным
шума, выраженный в формуле (3.21), следовательно, можно считать просто равным ![]() . Выразить шум
. Выразить шум ![]() можно через вектор его коэффициентов, подобно тому, как это делалось для сигналов в формуле (3.12). Имеем
можно через вектор его коэффициентов, подобно тому, как это делалось для сигналов в формуле (3.12). Имеем
![]() , (3.26)
, (3.26)
где ![]() - случайный вектор с нулевым средним и гауссовым распределением, а компоненты шума
- случайный вектор с нулевым средним и гауссовым распределением, а компоненты шума ![]() ,
, ![]() являются независимыми.
являются независимыми.
3.1.3.4. Дисперсия белого шума
Белый шум - это идеализированный процесс с двусторонней спектральной плотностью мощности, равной постоянной величине ![]() для всех частот от
для всех частот от ![]() до
до ![]() . Следовательно, дисперсия шума (средняя мощность шума, поскольку шум имеет нулевое среднее) равна следующему.
. Следовательно, дисперсия шума (средняя мощность шума, поскольку шум имеет нулевое среднее) равна следующему.
![]() (3.27)
(3.27)
Хотя дисперсия AWGN равна бесконечности, дисперсия фильтрованного шума AWGN конечна. Например, если AWGN коррелирует с одной из набора ортонормированных функций ![]() , дисперсия на выходе коррелятора описывается следующим выражением.
, дисперсия на выходе коррелятора описывается следующим выражением.
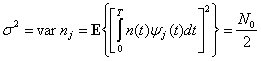 (3.28)
(3.28)
Доказательство формулы (3.28) приводится в приложении В. С этого момента будем считать, что интересующий нас шум процесса обнаружения является шумом на выходе коррелятора или согласованного фильтра с дисперсией ![]() , как указано в формуле (3.28).
, как указано в формуле (3.28).
3.1.4. Важнейший параметр систем цифровой связи - отношение сигнал/шум
Любой, кто изучал аналоговую связь, знаком с критерием качества, именуемым отношением средней мощности сигнала к средней мощности шума (S/N или SNR). В цифровой связи в качестве критерия качества чаще используется нормированная версия SNR, ![]() .
. ![]() - это энергия бита, и ее можно описать как мощность сигнала S, умноженную на время передачи бита
- это энергия бита, и ее можно описать как мощность сигнала S, умноженную на время передачи бита ![]() .
. ![]() - это спектральная плотность мощности шума, и ее можно выразить как мощность шума N, деленную на ширину полосы W. Поскольку время передачи бита и скорость передачи битов
- это спектральная плотность мощности шума, и ее можно выразить как мощность шума N, деленную на ширину полосы W. Поскольку время передачи бита и скорость передачи битов ![]() , взаимно обратны,
, взаимно обратны, ![]() можно заменить на
можно заменить на ![]() .
.
![]() (3.29)
(3.29)
Еще одним параметром, часто используемым в цифровой связи, является скорость передачи данных в битах в секунду. В целях упрощения выражений, встречающихся в книге, для представления скорости передачи битов вместо записи ![]() будем писать просто R. С учетом сказанного перепишем, выражение (3,29) так, чтобы было явно видно, что отношение
будем писать просто R. С учетом сказанного перепишем, выражение (3,29) так, чтобы было явно видно, что отношение ![]() представляет собой отношение S/N, нормированное на ширину полосы и скорость передачи битов.
представляет собой отношение S/N, нормированное на ширину полосы и скорость передачи битов.
![]() (3.30)
(3.30)
Одной из важнейших метрик производительности в системах цифровой связи является график зависимости вероятности появления ошибочного бита ![]() от
от ![]() . На рис. 3.6 показан «водопадоподобный» вид большинства подобных кривых. При
. На рис. 3.6 показан «водопадоподобный» вид большинства подобных кривых. При ![]() ,
, ![]() . Безразмерное отношение
. Безразмерное отношение ![]() - это стандартная качественная мера производительности систем цифровой связи. Следовательно, необходимое отношение
- это стандартная качественная мера производительности систем цифровой связи. Следовательно, необходимое отношение ![]() можно рассматривать как метрику, позволяющую сравнивать производительность различных систем; чем меньше требуемое отношение
можно рассматривать как метрику, позволяющую сравнивать производительность различных систем; чем меньше требуемое отношение ![]() , тем эффективнее процесс обнаружения при данной вероятности ошибки.
, тем эффективнее процесс обнаружения при данной вероятности ошибки.
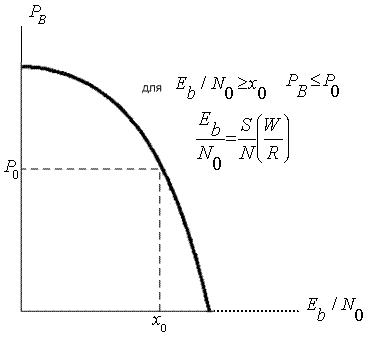
Рис. 3.6. Общий вид зависимости ![]() от
от ![]() .
.
3.1.5. Почему отношение 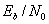 - это естественный критерий качества
- это естественный критерий качества
У неспециалистов в области цифровой связи может возникнуть вопрос о полезности параметра ![]() . Отношение S/N - это удобный критерий качества для аналоговых систем связи: числитель представляет меру мощности сигнала, которую желательно сохранить, а знаменатель - ухудшение вследствие электрических помех. Более того, отношение S/N интуитивно воспринимается как мера качества. Итак, почему в цифровых системах связи мы не можем продолжать использовать отношение S/N как критерий качества? Зачем для цифровых систем нужна другая метрика - отношение энергии бита к спектральной плотности мощности шума? Объяснению этого вопроса и посвящен данный раздел.
. Отношение S/N - это удобный критерий качества для аналоговых систем связи: числитель представляет меру мощности сигнала, которую желательно сохранить, а знаменатель - ухудшение вследствие электрических помех. Более того, отношение S/N интуитивно воспринимается как мера качества. Итак, почему в цифровых системах связи мы не можем продолжать использовать отношение S/N как критерий качества? Зачем для цифровых систем нужна другая метрика - отношение энергии бита к спектральной плотности мощности шума? Объяснению этого вопроса и посвящен данный раздел.
В разделе 1.2.4 сигнал в представлении через мощность определялся как сигнал с конечной средней мощностью и бесконечной энергией. Энергетический сигнал определялся как сигнал с нулевой средней мощностью и конечной энергией. Подобная классификация полезна при сравнении аналоговых и цифровых сигналов. Аналоговый сигнал мы относим к сигналам, представляемым через мощность. Почему это имеет смысл? Об аналоговом сигнале можно думать как о сигнале, имеющем бесконечную длительность, который не требуется разграничивать во времени. Неограниченно длительный аналоговый сигнал содержит бесконечную энергию; следовательно, использование энергии - это не самый удобный способ описания характеристик такого сигнала. Значительно более удобным параметром для аналоговых волн является мощность (или скорость доставки энергии).
В то же время в системах цифровой связи мы передаем (и принимаем) символы путем передачи некоторого сигнала в течение конечного промежутка времени, времени передачи символа ![]() . Сконцентрировав внимание на одном символе, видим, что мощность (усредненная по времени) стремится к нулю. Значит, для описания характеристик цифрового сигнала мощность не подходит. Для подобного сигнала нам нужна метрика, «достаточно хорошая» в пределах конечного промежутка времени. Другими словами, энергия символа (мощность, проинтегрированная по
. Сконцентрировав внимание на одном символе, видим, что мощность (усредненная по времени) стремится к нулю. Значит, для описания характеристик цифрового сигнала мощность не подходит. Для подобного сигнала нам нужна метрика, «достаточно хорошая» в пределах конечного промежутка времени. Другими словами, энергия символа (мощность, проинтегрированная по ![]() ) - это гораздо более удобный параметр описания цифровых сигналов.
) - это гораздо более удобный параметр описания цифровых сигналов.
То, что цифровой сигнал лучше всего характеризует полученная им энергия, еще не дает ответа на вопрос, почему ![]() - это естественная метрика для цифровых систем, так что продолжим. Цифровой сигнал - это транспортное средство, представляющее цифровое сообщение. Сообщение может содержать один бит (двоичное сообщение), два (четверичное),..., 10 бит (1024-ричное). В аналоговых системах нет ничего подобного такой дискретной структуре сообщения. Аналоговый информационный источник - это бесконечно квантованная непрерывная волна. Для цифровых систем критерий качества должен позволять сравнивать одну систему с другой на битовом уровне. Следовательно, описывать цифровые сигналы в терминах S/N практически бесполезно, поскольку сигнал может иметь однобитовое, 2-битовое или 10-битовое значение. Предположим, что для данной вероятности возникновения ошибки в цифровом двоичном сигнале требуемое отношение S/N равно 20. Будем считать, что понятия сигнала и его значения взаимозаменяемы. Поскольку двоичный сигнал имеет однобитовое значение, требуемое отношение S/N на бит равно 20 единицам. Предположим, что наш сигнал является 1024-ричным, с теми же 20 единицами требуемого отношения S/N. Теперь, поскольку сигнал имеет 10-битовое значение, требуемое отношение S/N на один бит равно всего 2. Возникает вопрос: почему мы должны выполнять такую цепочку вычислений, чтобы найти метрику, представляющую критерий качества? Почему бы сразу не выразить метрику через то, что нам действительно надо, - параметр, связанный с энергией на битовом уровне,
- это естественная метрика для цифровых систем, так что продолжим. Цифровой сигнал - это транспортное средство, представляющее цифровое сообщение. Сообщение может содержать один бит (двоичное сообщение), два (четверичное),..., 10 бит (1024-ричное). В аналоговых системах нет ничего подобного такой дискретной структуре сообщения. Аналоговый информационный источник - это бесконечно квантованная непрерывная волна. Для цифровых систем критерий качества должен позволять сравнивать одну систему с другой на битовом уровне. Следовательно, описывать цифровые сигналы в терминах S/N практически бесполезно, поскольку сигнал может иметь однобитовое, 2-битовое или 10-битовое значение. Предположим, что для данной вероятности возникновения ошибки в цифровом двоичном сигнале требуемое отношение S/N равно 20. Будем считать, что понятия сигнала и его значения взаимозаменяемы. Поскольку двоичный сигнал имеет однобитовое значение, требуемое отношение S/N на бит равно 20 единицам. Предположим, что наш сигнал является 1024-ричным, с теми же 20 единицами требуемого отношения S/N. Теперь, поскольку сигнал имеет 10-битовое значение, требуемое отношение S/N на один бит равно всего 2. Возникает вопрос: почему мы должны выполнять такую цепочку вычислений, чтобы найти метрику, представляющую критерий качества? Почему бы сразу не выразить метрику через то, что нам действительно надо, - параметр, связанный с энергией на битовом уровне, ![]() ? В заключение отметим, что поскольку отношение S/N является безразмерным, таким же есть и отношение
? В заключение отметим, что поскольку отношение S/N является безразмерным, таким же есть и отношение ![]() . Для проверки можно вычислить единицы измерения.
. Для проверки можно вычислить единицы измерения.
![]()
3.2. Обнаружение двоичных сигналов в гауссовом шуме
3.2.1. Критерий максимального правдоподобия приема сигналов
Критерий принятия решения, используемый в этапе 2 (рис. 3.1), описывался формулой (3.7) следующим образом.
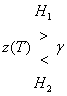
Популярный критерий выбора порога ![]() для принятия двоичного решения в выражении (3.7) основан на минимизации вероятности ошибки. Вычисление этого минимального значения ошибки
для принятия двоичного решения в выражении (3.7) основан на минимизации вероятности ошибки. Вычисление этого минимального значения ошибки ![]() начинается с записи связи отношения плотностей условных вероятностей и отношения априорных вероятностей появления сигнала. Поскольку плотность условной вероятности
начинается с записи связи отношения плотностей условных вероятностей и отношения априорных вероятностей появления сигнала. Поскольку плотность условной вероятности ![]() также называется правдоподобием
также называется правдоподобием ![]() , формулировка
, формулировка
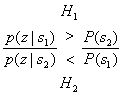 (3.31)
(3.31)
есть критерием отношения правдоподобий (см. приложение Б). В этом неравенстве ![]() и
и ![]() являются априорными вероятностями передачи сигналов
являются априорными вероятностями передачи сигналов ![]() и
и ![]() , a
, a ![]() и
и ![]() - две возможные гипотезы. Правило минимизации вероятности ошибки (формула (3.31)) гласит, что если отношение правдоподобий больше отношения априорных вероятностей, то следует выбирать гипотезу
- две возможные гипотезы. Правило минимизации вероятности ошибки (формула (3.31)) гласит, что если отношение правдоподобий больше отношения априорных вероятностей, то следует выбирать гипотезу ![]() .
.
В разделе Б.3.1 показано, что при ![]() и симметричных
и симметричных ![]()
![]() правдоподобиях подстановка формул (3.5) и (3.6) в формулу (3.31) дает
правдоподобиях подстановка формул (3.5) и (3.6) в формулу (3.31) дает
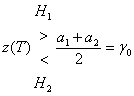 , (3.32)
, (3.32)
где ![]() - сигнальный компонент
- сигнальный компонент ![]() при передаче
при передаче ![]() , a
, a ![]() - сигнальный компонент при передаче
- сигнальный компонент при передаче ![]() . Порог
. Порог ![]() , представленный выражением
, представленный выражением ![]() , - это оптимальный порог для минимизации вероятности принятия неверного решения в этом важном частном случае. Описанный подход называется критерием минимальной ошибки.
, - это оптимальный порог для минимизации вероятности принятия неверного решения в этом важном частном случае. Описанный подход называется критерием минимальной ошибки.
Для равновероятных сигналов оптимальный порог ![]() , как показано на рис. 3.2, проходит через пересечение функций правдоподобия. Следовательно, используя формулу (3.32), видим, что этап принятия решения заключается в эффективном выборе гипотезы, соответствующей сигналу с максимальным правдоподобием. Пусть, например, значение выборки принятого сигнала равно
, как показано на рис. 3.2, проходит через пересечение функций правдоподобия. Следовательно, используя формулу (3.32), видим, что этап принятия решения заключается в эффективном выборе гипотезы, соответствующей сигналу с максимальным правдоподобием. Пусть, например, значение выборки принятого сигнала равно ![]() , а правдоподобия того, что
, а правдоподобия того, что ![]() принадлежит к одному из двух классов
принадлежит к одному из двух классов ![]() или
или ![]() , отличны от нуля. В этом случае критерий принятия решения можно рассматривать как сравнение правдоподобий
, отличны от нуля. В этом случае критерий принятия решения можно рассматривать как сравнение правдоподобий ![]() и
и ![]() . Более вероятное значение переданного сигнала соответствует наибольшей плотности вероятности. Другими словами, детектор выбирает
. Более вероятное значение переданного сигнала соответствует наибольшей плотности вероятности. Другими словами, детектор выбирает ![]() , если
, если
![]() (3.33)
(3.33)
В противном случае детектор выбирает ![]() . Детектор, минимизирующий вероятность ошибки (для классов равновероятных сигналов), называется детектором максимального правдоподобия.
. Детектор, минимизирующий вероятность ошибки (для классов равновероятных сигналов), называется детектором максимального правдоподобия.
Из рис. 3.2 можно видеть, что выражение (3.32) - это «метод здравого смысла» принятия решения при наличии статистических знаний о классах. Имея на выходе детектора значение ![]() , видим (рис. 3.2), что
, видим (рис. 3.2), что ![]() пересекается с графиком правдоподобия
пересекается с графиком правдоподобия ![]() в точке
в точке ![]() и с графиком правдоподобия
и с графиком правдоподобия ![]() в точке
в точке ![]() . Какое наиболее разумное решение должен принять детектор? В описанном случае наиболее здравым является выбор класса
. Какое наиболее разумное решение должен принять детектор? В описанном случае наиболее здравым является выбор класса ![]() , имеющего большее правдоподобие. Если бы пример был М-мерным, а не бинарным, всего существовало бы М функций правдоподобия, представляющих М классов сигналов, к которым может принадлежать принятый сигнал. Решение по принципу максимального правдоподобия в этом случае представляло бы выбор класса, имеющего самое большое правдоподобие из М возможных. (Основы теории принятия решений даются в приложении Б.)
, имеющего большее правдоподобие. Если бы пример был М-мерным, а не бинарным, всего существовало бы М функций правдоподобия, представляющих М классов сигналов, к которым может принадлежать принятый сигнал. Решение по принципу максимального правдоподобия в этом случае представляло бы выбор класса, имеющего самое большое правдоподобие из М возможных. (Основы теории принятия решений даются в приложении Б.)
3.2.1.1. Вероятность ошибки
В процессе принятия бинарного решения, показанном на рис. 3.2, существует две возможности возникновения ошибки. Ошибка ![]() появится при передаче
появится при передаче ![]() , если вследствие шума канала уровень переданного сигнала
, если вследствие шума канала уровень переданного сигнала ![]() упадет ниже
упадет ниже ![]() . Вероятность этого равна следующему.
. Вероятность этого равна следующему.
![]() (3.34)
(3.34)
Эта возможность показана заштрихованной областью слева от ![]() (рис. 3.2). Подобным образом ошибка появляется при передаче
(рис. 3.2). Подобным образом ошибка появляется при передаче ![]() , если вследствие шума канала уровень переданного сигнала
, если вследствие шума канала уровень переданного сигнала ![]() поднимется выше
поднимется выше ![]() . Вероятность этого равна следующему.
. Вероятность этого равна следующему.
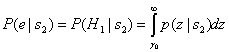 (3.35)
(3.35)
Суммарная вероятность ошибки равна сумме вероятностей всех возможностей ее появления. Для бинарного случая вероятность возникновения ошибочного бита можно выразить следующим образом.
![]() (3.36)
(3.36)
Объединяя формулы (3.34)-(3.36), получаем
![]() (3.37,а)
(3.37,а)
или, что равносильно,
![]() (3.37,б)
(3.37,б)
Иными словами, при передаче сигнала ![]() ошибка происходит при выборе гипотезы
ошибка происходит при выборе гипотезы ![]() ; или при передаче сигнала
; или при передаче сигнала ![]() ошибка происходит при выборе гипотезы
ошибка происходит при выборе гипотезы ![]() . Для равных априорных вероятностей (т.е.
. Для равных априорных вероятностей (т.е. ![]() ) имеем следующее.
) имеем следующее.
![]() (3.38)
(3.38)
Используя симметричность плотностей вероятности, получаем следующее.
![]() (3.39)
(3.39)
Вероятность появления ошибочного бита, ![]() , численно равна площади под «хвостом» любой функции правдоподобия,
, численно равна площади под «хвостом» любой функции правдоподобия, ![]() или
или ![]() , «заползающим» на «неправильную» сторону порога. Таким образом, для вычисления
, «заползающим» на «неправильную» сторону порога. Таким образом, для вычисления ![]() мы можем проинтегрировать
мы можем проинтегрировать
![]() от
от ![]() до
до ![]() или
или ![]() - от
- от ![]() до
до ![]() .
.
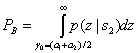 (3.40)
(3.40)
Здесь ![]() - оптимальный порог из уравнения (3.32). Заменяя правдоподобие
- оптимальный порог из уравнения (3.32). Заменяя правдоподобие ![]() его гауссовым эквивалентом из формулы (3.6), имеем
его гауссовым эквивалентом из формулы (3.6), имеем
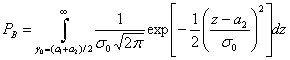 (3.41)
(3.41)
где ![]() - дисперсия шума вне коррелятора.
- дисперсия шума вне коррелятора.
Сделаем замену ![]() . Тогда
. Тогда ![]() и
и
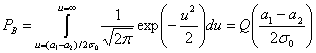 (3.42)
(3.42)
Здесь ![]() называется гауссовым интегралом ошибок и часто используется при описании вероятности с гауссовой плотностью распределения. Определяется эта функция следующим образом.
называется гауссовым интегралом ошибок и часто используется при описании вероятности с гауссовой плотностью распределения. Определяется эта функция следующим образом.
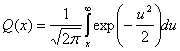 (3.43)
(3.43)
Отметим, что гауссов интеграл ошибок может определяться несколькими способами (см. приложение Б); впрочем, все определения одинаково пригодны для описания вероятности ошибки при гауссовом шуме. ![]() нельзя вычислить в аналитическом виде. В табл. Б.1 она представлена в форме таблицы. Хорошие аппроксимации функции
нельзя вычислить в аналитическом виде. В табл. Б.1 она представлена в форме таблицы. Хорошие аппроксимации функции ![]() через более простые функции можно найти в работе [5]. Вот одна из таких аппроксимаций, справедливая для
через более простые функции можно найти в работе [5]. Вот одна из таких аппроксимаций, справедливая для ![]() .
.
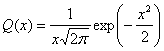 (3.44)
(3.44)
Итак, мы оптимизировали (в смысле минимизации ![]() ) порог
) порог ![]() , но не оптимизировали принимающий фильтр в блоке 1 (рис. 3.1). Далее нашей целью является оптимизация этого фильтра путем максимизации аргумента
, но не оптимизировали принимающий фильтр в блоке 1 (рис. 3.1). Далее нашей целью является оптимизация этого фильтра путем максимизации аргумента ![]() в формуле (3.42).
в формуле (3.42).
3.2.2. Согласованный фильтр
Согласованный фильтр (matched filter) - это линейное устройство, спроектированное, чтобы давать на выходе максимально возможное для данного передаваемого сигнала отношение сигнал/шум. Предположим, что на вход линейного, инвариантного относительно времени (принимающего) фильтра, за которым следует устройство дискретизации (рис. 3.1), подается известный сигнал ![]() плюс шум AWGN
плюс шум AWGN ![]() . В момент времени
. В момент времени ![]() сигнал на выходе устройства дискретизации
сигнал на выходе устройства дискретизации ![]() состоит из компонента сигнала
состоит из компонента сигнала ![]() , и компонента шума
, и компонента шума ![]() . Дисперсия шума на выходе (средняя мощность шума) записывается как
. Дисперсия шума на выходе (средняя мощность шума) записывается как ![]() , так что отношение мгновенной мощности шума к средней мощности шума,
, так что отношение мгновенной мощности шума к средней мощности шума, ![]() , в момент
, в момент ![]() вне устройства дискретизации на этапе 1 равно следующему.
вне устройства дискретизации на этапе 1 равно следующему.
![]() (3.45)
(3.45)
Нам нужно найти передаточную функцию фильтра ![]() с максимальным отношением
с максимальным отношением ![]() . Сигнал
. Сигнал ![]() на выходе фильтра можно выразить через передаточную функцию фильтра
на выходе фильтра можно выразить через передаточную функцию фильтра ![]() (до оптимизации) и Фурье-образ сигнала на входе
(до оптимизации) и Фурье-образ сигнала на входе
![]() , (3.46)
, (3.46)
где ![]() - Фурье-образ сигнала на входе,
- Фурье-образ сигнала на входе, ![]() . Если двусторонняя спектральная плотность мощности шума на входе равна
. Если двусторонняя спектральная плотность мощности шума на входе равна ![]() Вт/Гц, то с помощью формул (1.19) и (1.53) мощность шума на выходе можно записать следующим образом.
Вт/Гц, то с помощью формул (1.19) и (1.53) мощность шума на выходе можно записать следующим образом.
![]() (3.47)
(3.47)
Объединяя формулы (3.45) и (3.47), получаем выражение для ![]() .
.
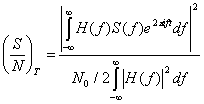 (3.48)
(3.48)
Найдем теперь значение ![]() , при котором
, при котором ![]() достигает максимума. Для этого нам понадобится неравенство Шварца, одна из форм записи которого представлена ниже.
достигает максимума. Для этого нам понадобится неравенство Шварца, одна из форм записи которого представлена ниже.
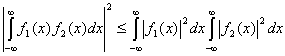 (3.49)
(3.49)
Равенство достигается при ![]() , где
, где ![]() - произвольная константа, а знак «*» обозначает комплексно сопряженное значение. Если отождествить
- произвольная константа, а знак «*» обозначает комплексно сопряженное значение. Если отождествить ![]() с
с ![]() и
и ![]() с
с ![]() , можем записать следующее.
, можем записать следующее.
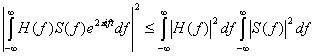 (3.50)
(3.50)
Подстановка в выражение (3.48) дает
![]() (3.51)
(3.51)
или
![]() , (3.52)
, (3.52)
где энергия Е входящего сигнала ![]() равна следующему.
равна следующему.
![]() (3.53)
(3.53)
Следовательно, максимальный выход ![]() зависит от энергии входящего сигнала и спектральной плотности мощности шума, но не от конкретной формы сигнала.
зависит от энергии входящего сигнала и спектральной плотности мощности шума, но не от конкретной формы сигнала.
Равенство в выражении (3.52) получается только при использовании оптимальной передаточной функции фильтра ![]() .
.
![]() (3.54)
(3.54)
или
![]() (3.55)
(3.55)
Поскольку ![]() - вещественный сигнал, с помощью формул (А.29) и (А.31) можно записать следующее.
- вещественный сигнал, с помощью формул (А.29) и (А.31) можно записать следующее.
![]()
![]()
![]()
![]() (3.56)
(3.56)
Итак, импульсная характеристика фильтра, дающего максимальное отношение сигнал/шум на выходе, является зеркальным отображением сигнала сообщения ![]() , запаздывающим на время передачи символа Т. Отметим, что задержка в Т секунд делает уравнение (3.56) причинным, т.е. запаздывание на Т секунд делает
, запаздывающим на время передачи символа Т. Отметим, что задержка в Т секунд делает уравнение (3.56) причинным, т.е. запаздывание на Т секунд делает ![]() функцией положительного времени в промежутке
функцией положительного времени в промежутке ![]() , Без задержки в Т секунд отклик
, Без задержки в Т секунд отклик ![]() нереализуем, поскольку в этом случае он является функцией отрицательного времени.
нереализуем, поскольку в этом случае он является функцией отрицательного времени.
3.2.3. Реализация корреляции в согласованном фильтре
В формуле (3.56) и на рис. 3.7, а отражено основное свойство согласованного фильтра: импульсная характеристика такого фильтра - это зеркальное отображение сигнала с некоторой задержкой (относительно оси ![]() ). Следовательно, если сигнал равен
). Следовательно, если сигнал равен ![]() , его зеркальное отображение равно
, его зеркальное отображение равно ![]() , а зеркальное отображение, запаздывающее на Т секунд, - это
, а зеркальное отображение, запаздывающее на Т секунд, - это ![]() . Выход
. Выход ![]() причинного фильтра во временной области можно описать как свертку принятого входного сигнала
причинного фильтра во временной области можно описать как свертку принятого входного сигнала ![]() с импульсной характеристикой фильтра (см. раздел А.5).
с импульсной характеристикой фильтра (см. раздел А.5).
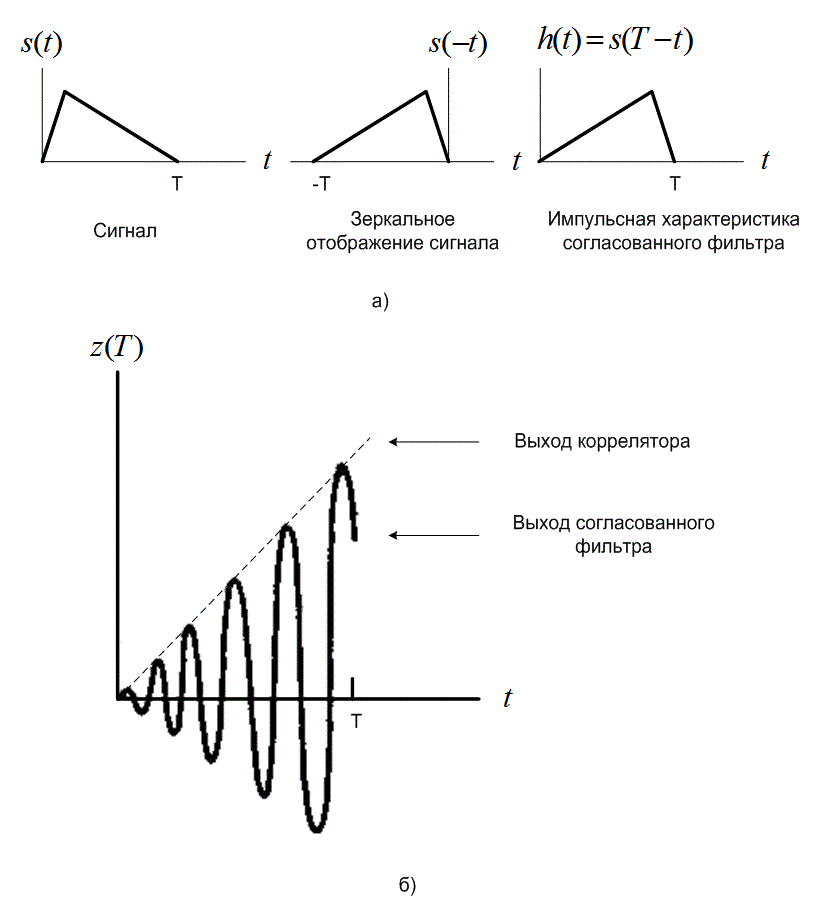
Рис.3.7. Коррелятор и согласованный фильтр: а) характеристика согласованного фильтра; б) сравнение выходов коррелятора и согласованного фильтра
Подставляя ![]() из формулы (3.56) в
из формулы (3.56) в ![]() в формуле (3.57) и выбирая произвольную константу
в формуле (3.57) и выбирая произвольную константу ![]() равной единице, получаем следующее.
равной единице, получаем следующее.
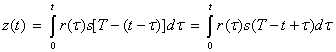 (3.58)
(3.58)
Для момента времени ![]() формулу (3.58) можно переписать следующим образом.
формулу (3.58) можно переписать следующим образом.
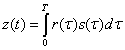 (3.59)
(3.59)
Из последнего выражения видно, что интеграл от произведения принятого сигнала ![]() на копию переданного сигнала
на копию переданного сигнала ![]() на интервале передачи символа представляет собой корреляцию
на интервале передачи символа представляет собой корреляцию ![]() с
с ![]() . Предположим, что принятый сигнал
. Предположим, что принятый сигнал ![]() коррелирует со всеми Сигналами-прототипами
коррелирует со всеми Сигналами-прототипами ![]()
![]() и для этого используется набор из М корреляторов. Сигнал
и для этого используется набор из М корреляторов. Сигнал ![]() , корреляция которого (или интеграл от произведения) с
, корреляция которого (или интеграл от произведения) с ![]() дает максимальное значение
дает максимальное значение ![]() , - и есть сигнал, который согласуется с
, - и есть сигнал, который согласуется с ![]() лучше остальных. Далее это свойство корреляции мы будем использовать для оптимального обнаружения сигналов.
лучше остальных. Далее это свойство корреляции мы будем использовать для оптимального обнаружения сигналов.
3.2.3.1. Сравнение свертки и корреляции
Работа согласованного фильтра описывается математической операцией свертки; сигнал сворачивается с импульсной характеристикой фильтра. Работа коррелятора описывается математической операцией корреляции; сигнал коррелирует с копией самого себя. Довольно часто термин «согласованный фильтр» используется как синоним термина «коррелятор». Как такое возможно, если математические операции различны? Напомним, что процесс свертки двух сигналов использует один из сигналов, обращенный во времени. Кроме того, импульсная характеристика согласованного фильтра определяется именно через сигнал, обращенный во времени. Следовательно, свертка в согласованном фильтре с обращенной во времени функцией дает еще одно обращение во времени, подавая на выход (в конце интервала передачи символа) то, что является корреляцией сигнала с собственной копией. Значит, принимающий фильтр, изображенный на рис. 3.1, можно реализовать либо как согласованный фильтр, либо как коррелятор. Важно отметить, что выходы коррелятора и согласованного фильтра одинаковы только в момент времени ![]() . Для синусоидального входа выход коррелятора,
. Для синусоидального входа выход коррелятора, ![]() , на промежутке
, на промежутке ![]() приблизительно описывается линейной функцией. В то же время выход согласованного фильтра приблизительно описывается синусоидой, амплитуда которой в том же промежутке времени модулирована линейной функцией (см. рис. 3.7, б). Поскольку при соизмеримых входах выходы согласованного фильтра и коррелятора идентичны в момент взятия выборки
приблизительно описывается линейной функцией. В то же время выход согласованного фильтра приблизительно описывается синусоидой, амплитуда которой в том же промежутке времени модулирована линейной функцией (см. рис. 3.7, б). Поскольку при соизмеримых входах выходы согласованного фильтра и коррелятора идентичны в момент взятия выборки ![]() , функции согласованного фильтра и коррелятора, изображенные на рис. 3.8, часто используются как взаимозаменяемые.
, функции согласованного фильтра и коррелятора, изображенные на рис. 3.8, часто используются как взаимозаменяемые.
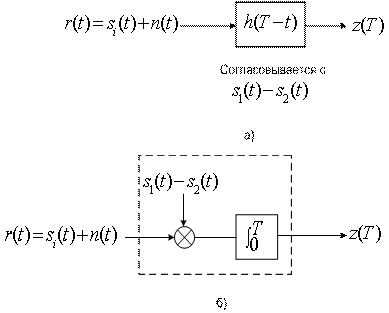
Рис.3.8. Эквивалентность согласованного фильтра и коррелятора:
а) согласованный фильтр; б) коррелятор
3.2.3.2. Дилемма в представлении упорядоченных во времени событий
При представлении упорядоченных во времени событий существует серьезная проблема. Возникает частая ошибка в области электротехники - путаница между самым старшим битом и самым младшим. На рис. 3.9, а показано, как обычно изображается функция времени; самое раннее событие представлено слева, а наиболее позднее - справа. Людям, привыкшим читать слева направо, такое изображение кажется единственно правильным. Рассмотрим рис. 3.9, б, где показано, как импульсы поступают в сеть (или канал) и покидают ее. Здесь самое раннее событие изображено справа, а наиболее позднее - слева. Изучение этого рисунка позволяет понять, что при записи упорядоченных событий возможна путаница между двумя возможными форматами записи. Чтобы избежать затруднений, зачастую необходимо дать некоторые пояснения (например, указать, что крайний справа бит - это первый бит).
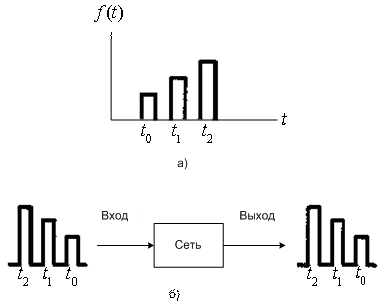
Рис.3.9. Дилемма в представлении упорядоченных во времени событий
Математические соотношения часто имеют «врожденные» особенности, гарантирующие соответствующее упорядочение событий. Например, в разделе 3.2.3 согласованный фильтр определялся как имеющий импульсную характеристику ![]() - запаздывающую версию обращенной во времени копии сигнала. Иными словами,
- запаздывающую версию обращенной во времени копии сигнала. Иными словами, ![]() . Запаздывание на один интервал передачи символа Т необходимо для того, чтобы фильтр был причинным (выход должен быть функцией положительного времени). Обращение во времени можно рассматривать как «предварительную коррекцию», где крайняя правая часть временного графика теперь соответствует наиболее раннему событию. Поскольку свертка навязывает другое обращение во времени, поступающий сигнал и импульсный отклик фильтра будут «идти в ногу» (ранний с ранним, поздний с поздним).
. Запаздывание на один интервал передачи символа Т необходимо для того, чтобы фильтр был причинным (выход должен быть функцией положительного времени). Обращение во времени можно рассматривать как «предварительную коррекцию», где крайняя правая часть временного графика теперь соответствует наиболее раннему событию. Поскольку свертка навязывает другое обращение во времени, поступающий сигнал и импульсный отклик фильтра будут «идти в ногу» (ранний с ранним, поздний с поздним).
3.2.4. Оптимизация вероятности ошибки
Для оптимизации (минимизации) ![]() в среде канала и приемника с шумом AWGN, показанных на рис. 3.1, нужно выбрать оптимальный принимающий фильтр на этапе 1 и оптимальный порог принятия решения на этапе 2. Для двоичного случая оптимальный порог принятия решения уже выбран и дается формулой (3.32), а в формуле (3.42) показано, что вероятность ошибки при таком пороге равна
в среде канала и приемника с шумом AWGN, показанных на рис. 3.1, нужно выбрать оптимальный принимающий фильтр на этапе 1 и оптимальный порог принятия решения на этапе 2. Для двоичного случая оптимальный порог принятия решения уже выбран и дается формулой (3.32), а в формуле (3.42) показано, что вероятность ошибки при таком пороге равна ![]() . Для минимального
. Для минимального ![]() в общем случае необходимо выбрать фильтр (согласованный) с максимальным аргументом функции
в общем случае необходимо выбрать фильтр (согласованный) с максимальным аргументом функции ![]() . Следовательно, нужно определить максимальное
. Следовательно, нужно определить максимальное ![]() , что равносильно максимальному
, что равносильно максимальному
![]() , (3.60)
, (3.60)
где ![]() - разность желательных компонентов сигнала на выходе фильтра в момент
- разность желательных компонентов сигнала на выходе фильтра в момент ![]() , а квадрат этого разностного сигнала представляет его мгновенную мощность. В разделе 3.2.2 описывался согласованный фильтр с максимальным отношением сигнал/шум (signal-to-noise ratio - SNR) для данного известного сигнала. Здесь мы решаем вопрос двоичной передачи сигналов и ищем оптимальный фильтр с максимальной разностью двух возможных выходных сигналов. В выводе, приведенном в уравнениях (3.45)-(3.52), было показано, что согласованный фильтр дает на выходе максимально возможное отношение SNR, равное
, а квадрат этого разностного сигнала представляет его мгновенную мощность. В разделе 3.2.2 описывался согласованный фильтр с максимальным отношением сигнал/шум (signal-to-noise ratio - SNR) для данного известного сигнала. Здесь мы решаем вопрос двоичной передачи сигналов и ищем оптимальный фильтр с максимальной разностью двух возможных выходных сигналов. В выводе, приведенном в уравнениях (3.45)-(3.52), было показано, что согласованный фильтр дает на выходе максимально возможное отношение SNR, равное ![]() . Допустим, что фильтр согласовывает входящий разностный сигнал
. Допустим, что фильтр согласовывает входящий разностный сигнал ![]() . Следовательно, в момент
. Следовательно, в момент ![]() можем записать отношение SNR на выходе.
можем записать отношение SNR на выходе.
![]() , (3.61)
, (3.61)
где ![]() - двусторонняя спектральная плотность мощности шума на входе фильтра и
- двусторонняя спектральная плотность мощности шума на входе фильтра и
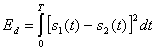 (3.62)
(3.62)
является энергией разностного сигнала на входе фильтра. Отметим, что уравнение (3.61) не представляет отношения SNR для какой-то отдельной передачи, ![]() или
или ![]() . Это отношение дает метрику разности сигналов на выходе фильтра. Максимизируя выходное отношение SNR, как показано в уравнении (3.61), согласованный фильтр обеспечивает максимальное расстояние (нормированное на шум) между двумя возможными выходами – сигналами
. Это отношение дает метрику разности сигналов на выходе фильтра. Максимизируя выходное отношение SNR, как показано в уравнении (3.61), согласованный фильтр обеспечивает максимальное расстояние (нормированное на шум) между двумя возможными выходами – сигналами ![]() и
и ![]() .
.
Далее, объединяя уравнения (3.42) и (3.61), получаем следующее.
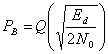 (3.63)
(3.63)
Для согласованного фильтра уравнение (3.63) является важным промежуточным результатом, включающим энергию разностного сигнала на входе фильтра. Из этого уравнения можно вывести более общее соотношение для энергии принятого бита. Для начала определим временной коэффициент взаимной корреляции ![]() , который будем использовать в качестве меры подобия двух сигналов
, который будем использовать в качестве меры подобия двух сигналов ![]() и
и ![]() . Имеем
. Имеем
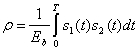 (3.64,а)
(3.64,а)
и
![]() (3.64,б)
(3.64,б)
где ![]() . Формула (3.64,а) - это классический математический способ выражения корреляции. Впрочем, если рассматривать
. Формула (3.64,а) - это классический математический способ выражения корреляции. Впрочем, если рассматривать ![]() и
и ![]() как векторы сигналов
как векторы сигналов ![]() и
и ![]() , то более удобным представлением
, то более удобным представлением ![]() является формула (3.64,6). Векторное представление позволяет получать удобные графические изображения. Векторы
является формула (3.64,6). Векторное представление позволяет получать удобные графические изображения. Векторы ![]() и
и ![]() разделены углом
разделены углом ![]() ; при малом угле векторы достаточно подобны (сильно коррелируют), а при больших углах они отличаются. Косинус угла
; при малом угле векторы достаточно подобны (сильно коррелируют), а при больших углах они отличаются. Косинус угла ![]() дает ту же нормированную метрику корреляции, что и формула (3.64,а).
дает ту же нормированную метрику корреляции, что и формула (3.64,а).
Расписывая выражение (3.62), получаем следующее.
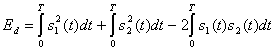 (3.65)
(3.65)
Напомним, что два первых члена формулы (3.65) представляют энергию, связанную с битом, ![]() .
.
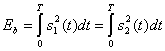 (3.66)
(3.66)
Подставляя уравнения (3.64,а) и (3.66) в формулу (3.65), получаем следующее.
![]() (3.67)
(3.67)
Подставляя уравнение (3.67) в (3.63), получаем следующее.
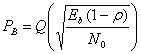 (3.68)
(3.68)
Рассмотрим случай ![]() , соответствующий наилучшей корреляции сигналов
, соответствующий наилучшей корреляции сигналов ![]() и
и ![]() в течение времени передачи символа (если сигналы изобразить как векторы, угол между ними будет равен нулю). Возможно ли, чтобы подобные сигналы использовались кем-то в реальной системе? Разумеется, нет, поскольку сигналы связи (элементы алфавита) должны быль максимально несопоставимы, чтобы их можно было легко различать (обнаруживать). В данный момент мы просто рассматриваем возможные значения
в течение времени передачи символа (если сигналы изобразить как векторы, угол между ними будет равен нулю). Возможно ли, чтобы подобные сигналы использовались кем-то в реальной системе? Разумеется, нет, поскольку сигналы связи (элементы алфавита) должны быль максимально несопоставимы, чтобы их можно было легко различать (обнаруживать). В данный момент мы просто рассматриваем возможные значения ![]() . Следующий частный случай
. Следующий частный случай ![]() соответствует «антикорреляции»
соответствует «антикорреляции» ![]() и
и ![]() в течение времени передачи символа. Другими словами, угол между векторами сигналов составляет 180°. В этом случае, когда векторы являются зеркальными отображениями друг друга, как показано на рис. 3.10, а, сигналы называются антиподными. Рассмотрим также случай
в течение времени передачи символа. Другими словами, угол между векторами сигналов составляет 180°. В этом случае, когда векторы являются зеркальными отображениями друг друга, как показано на рис. 3.10, а, сигналы называются антиподными. Рассмотрим также случай ![]() , соответствующий нулевой корреляции между
, соответствующий нулевой корреляции между ![]() и
и ![]() (угол между векторами равен 90°). Такие сигналы, показанные на рис. 3.10, б, именуются ортогональными. Чтобы два сигнала были ортогональными, они не должны коррелировать в течение времени передачи символа, т.е. должно выполняться следующее условие.
(угол между векторами равен 90°). Такие сигналы, показанные на рис. 3.10, б, именуются ортогональными. Чтобы два сигнала были ортогональными, они не должны коррелировать в течение времени передачи символа, т.е. должно выполняться следующее условие.
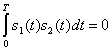 (3.69)
(3.69)
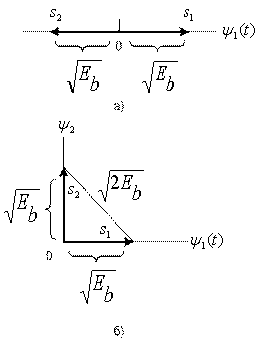
Рис. 3.10. Векторы двоичных сигналов: а) антиподные; б) ортогональные
Вопрос ортогональности рассматривался ранее, в разделе 3.1.3. При обнаружении антиподных сигналов (т.е. при ![]() ) с помощью согласованного фильтра, уравнение (3.68) можно записать следующим образом.
) с помощью согласованного фильтра, уравнение (3.68) можно записать следующим образом.
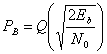 (3.70)
(3.70)
Точно так же при обнаружении ортогональных сигналов (т.е. при ![]() ) с помощью согласованного фильтра, формулу (3.68) можно записать следующим образом.
) с помощью согласованного фильтра, формулу (3.68) можно записать следующим образом.
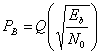 (3.71)
(3.71)
На рис. 3.10, где амплитуды сигналов выбраны равными ![]() , показано, что вероятность ошибки, описываемая уравнениями (3.70) и (3.71), является функцией расстояния между
, показано, что вероятность ошибки, описываемая уравнениями (3.70) и (3.71), является функцией расстояния между ![]() и
и ![]() (чем больше расстояние, тем меньше
(чем больше расстояние, тем меньше ![]() ). Если взять антиподные сигналы (рис. 3.10, а), расстояние между ними будет равно
). Если взять антиподные сигналы (рис. 3.10, а), расстояние между ними будет равно ![]() , а энергия
, а энергия ![]() , связанная с расстоянием, будет выражаться как квадрат расстояния, или
, связанная с расстоянием, будет выражаться как квадрат расстояния, или ![]() . При подстановке
. При подстановке ![]() в уравнение (3.63) получаем уравнение (3.70). Если взять ортогональные сигналы (рис. 3.10, б), расстояние между ними будет равно
в уравнение (3.63) получаем уравнение (3.70). Если взять ортогональные сигналы (рис. 3.10, б), расстояние между ними будет равно ![]() ; следовательно,
; следовательно, ![]() . При подстановке
. При подстановке ![]() в уравнение (3.63) получим уравнение (3.71).
в уравнение (3.63) получим уравнение (3.71).
Пример 3.2. Обнаружение антиподных сигналов с помощью согласованного фильтра
Рассмотрим бинарную систему связи, принимающую равновероятные сигналы ![]() и
и ![]() плюс шум AWGN (рис. 3.11). Предположим, что в качестве принимающего фильтра используется согласованный фильтр и спектральная плотность мощности шума
плюс шум AWGN (рис. 3.11). Предположим, что в качестве принимающего фильтра используется согласованный фильтр и спектральная плотность мощности шума ![]() равна
равна ![]() Вт/Гц. С помощью значения напряжения и времени принятого сигнала, показанных на рис. 3.11, вычислите вероятность появления ошибочного бита.
Вт/Гц. С помощью значения напряжения и времени принятого сигнала, показанных на рис. 3.11, вычислите вероятность появления ошибочного бита.
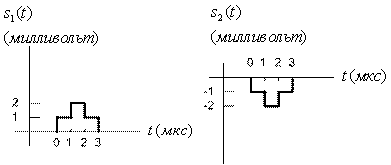
Рис.3.11. Узкополосные аналоговые сигналы
Решение
Мы можем графически определить отношение принятой энергии на бит сигнала, используя для этого один из двух графиков, либо ![]() , либо
, либо ![]() , представленных на рис. 3.11. Энергия - это площадь под графиком импульса, которая находится путем интегрирования.
, представленных на рис. 3.11. Энергия - это площадь под графиком импульса, которая находится путем интегрирования.
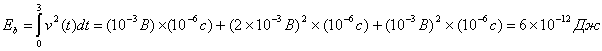
Поскольку сигналы, изображенные на рис. 3.11, являются антиподными и обнаруживаются с помощью согласованного фильтра, используем формулу (3.70) для вычисления вероятности появления ошибочного бита.
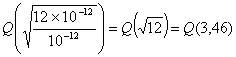
Из табл. Б.1 находим, что ![]() . Кроме того, поскольку аргумент
. Кроме того, поскольку аргумент ![]() больше 3, можно также использовать приближенное соотношение, приведенное в формуле (3.44), которое дает вероятность
больше 3, можно также использовать приближенное соотношение, приведенное в формуле (3.44), которое дает вероятность ![]() . Поскольку принятые сигналы являются антиподными и принимаются согласованным фильтром, весьма вероятно, что формула (3.70) дает верное выражение для нахождения вероятности возникновения ошибочного бита. Сигналы
. Поскольку принятые сигналы являются антиподными и принимаются согласованным фильтром, весьма вероятно, что формула (3.70) дает верное выражение для нахождения вероятности возникновения ошибочного бита. Сигналы ![]() и
и ![]() могут выглядеть гораздо более странно, но до тех пор, пока они являются антиподными и обнаруживаются с помощью согласованного фильтра, их внешний вид не влияет на вычисление
могут выглядеть гораздо более странно, но до тех пор, пока они являются антиподными и обнаруживаются с помощью согласованного фильтра, их внешний вид не влияет на вычисление ![]() . Формы сигналов, разумеется, имеют значение, но только когда дело доходит до определения импульсного отклика согласованного фильтра, необходимого для обнаружения этих сигналов.
. Формы сигналов, разумеется, имеют значение, но только когда дело доходит до определения импульсного отклика согласованного фильтра, необходимого для обнаружения этих сигналов.
3.2.5. Вероятность возникновения ошибки при двоичной передаче сигналов
3.2.5.1. Униполярная передача сигналов
На рис. 3.12, а приведен пример узкополосной ортогональной передачи сигналов, называемой униполярной.
![]()
![]()
![]()
![]()
![]() (3.72)
(3.72)
Здесь ![]() - амплитуда сигнала
- амплитуда сигнала ![]() . Определение ортогональной передачи сигналов дается выражением (3.69), требующим, чтобы
. Определение ортогональной передачи сигналов дается выражением (3.69), требующим, чтобы ![]() и
и ![]() имели нулевую корреляцию в течение периода передачи символа.
имели нулевую корреляцию в течение периода передачи символа.
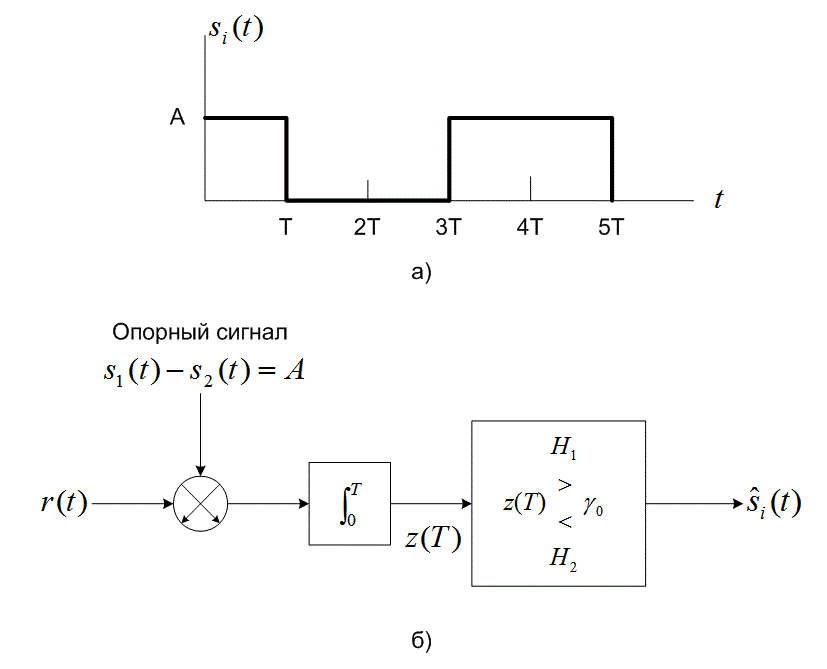
Рис.3.12. Обнаружение при униполярной узкополосной передаче сигналов:
а) пример униполярной передачи сигналов; б) обнаружение с помощью коррелятора
Поскольку в формуле (3.72) ![]() равно нулю в течение периода передачи символа, множество униполярных импульсов полностью удовлетворяет условию, приведенному в уравнении (3.69), а следовательно, они формируют ортогональное множество сигналов. Рассмотрим униполярную передачу сигналов (рис. 3.12, а) и коррелятор (рис. 3.12, б), который может использоваться для обнаружения подобных импульсов. Коррелятор перемножает входящий сигнал
равно нулю в течение периода передачи символа, множество униполярных импульсов полностью удовлетворяет условию, приведенному в уравнении (3.69), а следовательно, они формируют ортогональное множество сигналов. Рассмотрим униполярную передачу сигналов (рис. 3.12, а) и коррелятор (рис. 3.12, б), который может использоваться для обнаружения подобных импульсов. Коррелятор перемножает входящий сигнал ![]() и разность сигналов-прототипов,
и разность сигналов-прототипов, ![]() , после чего результат интегрируется. По окончании периода передачи символа Т устройство дискретизации (включающееся в момент, определенный как верхний предел интегрирования) дает тестовую статистику
, после чего результат интегрируется. По окончании периода передачи символа Т устройство дискретизации (включающееся в момент, определенный как верхний предел интегрирования) дает тестовую статистику ![]() , которая затем сравнивается с порогом
, которая затем сравнивается с порогом ![]() . В случае приема
. В случае приема ![]() и шума AWGN (т.е. когда
и шума AWGN (т.е. когда ![]() ) сигнальный компонент
) сигнальный компонент ![]() находится с помощью уравнения (3.69).
находится с помощью уравнения (3.69).
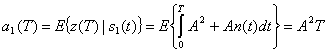
Здесь ![]() - математическое ожидание того, что при принятой выборке
- математическое ожидание того, что при принятой выборке ![]() был передан сигнал
был передан сигнал ![]() . Далее использовано равенство
. Далее использовано равенство ![]() . Подобным образом при
. Подобным образом при ![]() ,
, ![]() . Таким образом, в рассматриваемом случае оптимальный порог принятия решения (см. уравнение (3.32)) равен
. Таким образом, в рассматриваемом случае оптимальный порог принятия решения (см. уравнение (3.32)) равен ![]() . Если тестовая статистика
. Если тестовая статистика ![]() больше
больше ![]() , сигнал считается равным
, сигнал считается равным ![]() ; в противном случае принимается решение, что был передан сигнал
; в противном случае принимается решение, что был передан сигнал ![]() .
.
Из уравнения (3.62) получаем, что энергетический разностный сигнал равен ![]() . Тогда из формулы (3.63) получаем вероятность появления на выходе ошибочного бита.
. Тогда из формулы (3.63) получаем вероятность появления на выходе ошибочного бита.
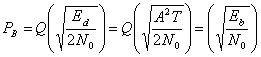 , (3.73)
, (3.73)
где при равновероятной передаче сигналов средняя энергия на бит равна ![]() . Уравнение (3.73) совпадает с уравнением (3.71), полученным с помощью общих рассуждений для ортогональной передачи сигналов.
. Уравнение (3.73) совпадает с уравнением (3.71), полученным с помощью общих рассуждений для ортогональной передачи сигналов.
Отметим, что вне блока перемножения, подобного показанному на рис. 3.12, б, единицей измерения сигнала является вольт. Следовательно, для сигналов напряжения на каждом из двух входов передаточная функция блока перемножения должна иметь размерность 1/вольт, а функция ![]() вне блока перемножения - вольт/вольт в квадрате. Подобным образом вне блока интегрирования также используется единица измерения вольт. Следовательно, для сигнала напряжения в блоке интегрирования передаточная функция интегратора должна иметь размерность 1/секунду, а значит, общая передаточная функция блока перемножения-интегрирования должна иметь размерность 1/вольт-секунда. Итак, для сигнала, поступающего на интегратор и имеющего размерность энергии (вольт в квадрате-секунда), получаем с выхода сигнал, пропорциональный энергии принятого сигнала (вольт/джоуль).
вне блока перемножения - вольт/вольт в квадрате. Подобным образом вне блока интегрирования также используется единица измерения вольт. Следовательно, для сигнала напряжения в блоке интегрирования передаточная функция интегратора должна иметь размерность 1/секунду, а значит, общая передаточная функция блока перемножения-интегрирования должна иметь размерность 1/вольт-секунда. Итак, для сигнала, поступающего на интегратор и имеющего размерность энергии (вольт в квадрате-секунда), получаем с выхода сигнал, пропорциональный энергии принятого сигнала (вольт/джоуль).
3.2.5.2. Биполярная передача сигналов
На рис. 3.13, а приведен пример узкополосной антиподной передачи сигналов, называемой биполярной, где
![]()
![]()
![]()
![]()
![]() (3.74)
(3.74)
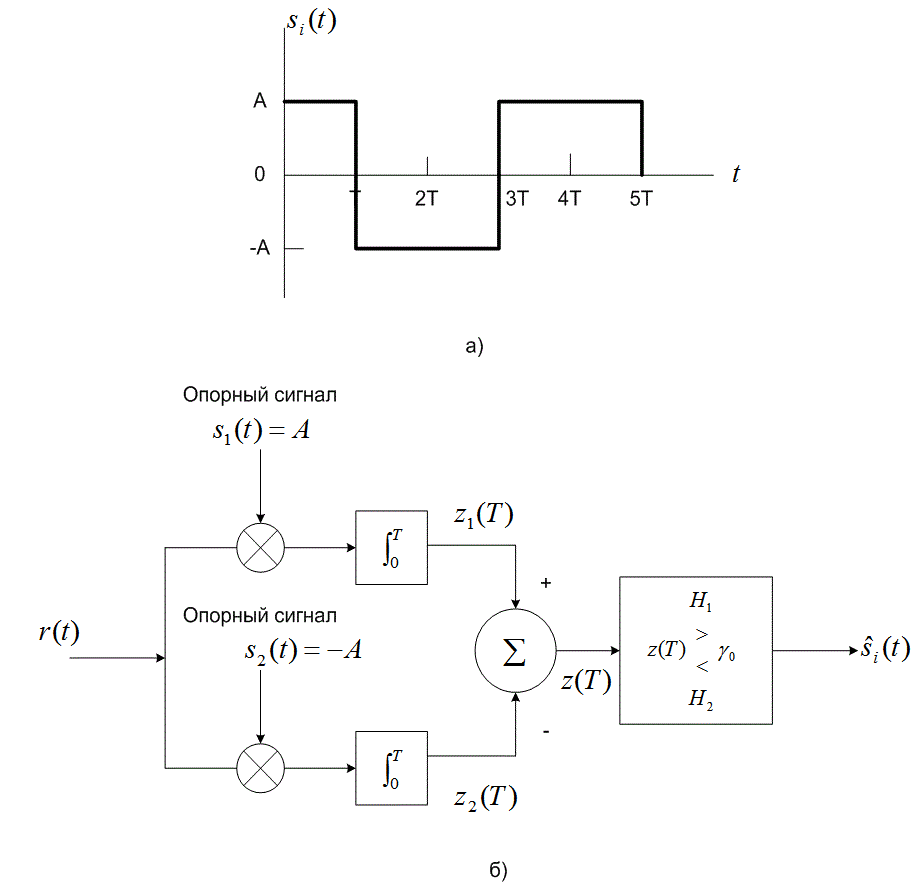
Рис.3.13. Обнаружение при биполярной узкополосной передаче сигналов: а) пример биполярной передачи сигналов; б) обнаружение с помощью коррелятора
Как определялось ранее, термин «антиподный» относится к двоичным сигналам, которые являются зеркальными отображениями друг друга, т.е. ![]() . Приемник-коррелятор таких антиподных сигналов может иметь схему, подобную представленной на рис. 3.13, б. Один коррелятор перемножает входящий сигнал
. Приемник-коррелятор таких антиподных сигналов может иметь схему, подобную представленной на рис. 3.13, б. Один коррелятор перемножает входящий сигнал ![]() и сигнал-прототип
и сигнал-прототип ![]() , после чего интегрирует результат; второй выполняет те же действия с сигналом
, после чего интегрирует результат; второй выполняет те же действия с сигналом ![]() .
.
На рис. 3.13, б изображена сама суть основной функции цифрового приемника. Иными словами, в течение периода передачи символа входящий зашумленный сигнал пускается по множественным различным «проходам» для проверки его корреляции со всеми возможными прототипами. После этого приемник определяет наибольшее выходное напряжение (наилучшее соответствие) и принимает соответствующее, решение относительно значения переданного символа. В бинарном случае имеем два возможных прототипа. В квадратичном случае могут существовать 4 возможности и т.д. На рис. 3.13, б выходы коррелятора обозначены как ![]()
![]() . Тестовая статистика, сформированная из разности выходов коррелятора, выглядит следующим образом.
. Тестовая статистика, сформированная из разности выходов коррелятора, выглядит следующим образом.
![]() (3.75)
(3.75)
Решение принимается с использованием порога, указанного в формуле (3.32). Для антиподных сигналов ![]() ; следовательно,
; следовательно, ![]() . Значит, если тестовая статистика
. Значит, если тестовая статистика ![]() положительна, считается, что передан сигнал
положительна, считается, что передан сигнал ![]() ; если же тестовая статистика отрицательна, считается, что передан сигнал
; если же тестовая статистика отрицательна, считается, что передан сигнал ![]() .
.
Из уравнения (3.62) энергетический разностный сигнал равен ![]() . Следовательно, можем использовать уравнение (3.63) для вычисления вероятности появления ошибочного бита.
. Следовательно, можем использовать уравнение (3.63) для вычисления вероятности появления ошибочного бита.
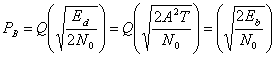 (3.76)
(3.76)
Здесь средняя энергия на бит равна ![]() . Уравнение (3.76) совпадает с уравнением (3.70), полученным с помощью общих рассуждений для ортогональной передачи сигналов.
. Уравнение (3.76) совпадает с уравнением (3.70), полученным с помощью общих рассуждений для ортогональной передачи сигналов.
3.2.5.3. Использование базисных функций для описания передачи сигналов
В корреляторе, приведенном на рис. 3.13, б, в качестве опорных могут использоваться не только сигналы ![]() ; с этой же целью могут применяться базисные функции, описанные в разделе 3.1.3. Проиллюстрируем этот подход на бинарной передаче сигналов с помощью униполярных или биполярных импульсов, поскольку в этом случае все сигнальное пространство можно охарактеризовать одной базисной функцией. Если нормировать пространство, т.е. в уравнении (3.76) положить
; с этой же целью могут применяться базисные функции, описанные в разделе 3.1.3. Проиллюстрируем этот подход на бинарной передаче сигналов с помощью униполярных или биполярных импульсов, поскольку в этом случае все сигнальное пространство можно охарактеризовать одной базисной функцией. Если нормировать пространство, т.е. в уравнении (3.76) положить ![]() , то базисная функция
, то базисная функция ![]() будет равна
будет равна ![]() .
.
Для униполярной передачи импульсов можем записать следующее.
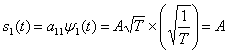
и
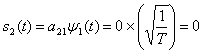
Здесь коэффициенты ![]() , и
, и ![]() равны, соответственно,
равны, соответственно, ![]() и
и ![]() .
.
Для биполярной передачи импульсов можем записать
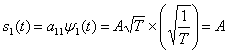
и
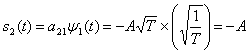
где коэффициенты ![]() и
и ![]() равны, Соответственно,
равны, Соответственно, ![]() и
и ![]() . При использовании антиподных импульсов можно считать, что приемник-коррелятор имеет вид, показанный на рис. 3.12, б, с опорным сигналом, равным
. При использовании антиподных импульсов можно считать, что приемник-коррелятор имеет вид, показанный на рис. 3.12, б, с опорным сигналом, равным ![]() . Итак, при передаче
. Итак, при передаче ![]() , можем записать следующее.
, можем записать следующее.
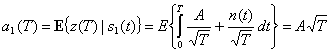
Поскольку ![]() , а значит для антиподной передачи сигналов
, а значит для антиподной передачи сигналов ![]() , то
, то ![]() . Аналогично при приеме сигнала
. Аналогично при приеме сигнала ![]() получаем
получаем ![]() . Если опорные сигналы рассматривать именно таким образом, то математическое ожидание
. Если опорные сигналы рассматривать именно таким образом, то математическое ожидание ![]() равно
равно ![]() (измеряется в нормированных вольтах, пропорциональных принятой энергии). Приведенный подход к описанию коррелятора дает удобное выражение
(измеряется в нормированных вольтах, пропорциональных принятой энергии). Приведенный подход к описанию коррелятора дает удобное выражение ![]() , имеющее те же единицы измерения (вольт), что используются вне блоков перемножения и интегрирования. Еще раз повторим важный момент: на выходе устройства дискретизации (в додетекторной точке) тестовая статистика
, имеющее те же единицы измерения (вольт), что используются вне блоков перемножения и интегрирования. Еще раз повторим важный момент: на выходе устройства дискретизации (в додетекторной точке) тестовая статистика ![]() - это сигнал напряжения, пропорциональный энергии принятого сигнала.
- это сигнал напряжения, пропорциональный энергии принятого сигнала.
На рис. 3.14 показана зависимость ![]() от
от ![]() для биполярной и униполярной передачи сигналов. Существует только два точных способа сравнения этих кривых. Проведем вертикальную линию при некотором данном отношении
для биполярной и униполярной передачи сигналов. Существует только два точных способа сравнения этих кривых. Проведем вертикальную линию при некотором данном отношении ![]() , скажем 10 дБ. Видим, что униполярная передача сигналов дает вероятность
, скажем 10 дБ. Видим, что униполярная передача сигналов дает вероятность ![]() порядка
порядка ![]() , а биполярная – порядка
, а биполярная – порядка ![]() . Нижняя кривая соответствует лучшей достоверности передачи. Можно также провести горизонтальную линию при некотором требуемом уровне
. Нижняя кривая соответствует лучшей достоверности передачи. Можно также провести горизонтальную линию при некотором требуемом уровне ![]() , скажем
, скажем ![]() . Видим, что при униполярной передаче сигналов каждый принятый бит потребует отношения
. Видим, что при униполярной передаче сигналов каждый принятый бит потребует отношения ![]() порядка 12,5 дБ, а при биполярной передаче - не более 9,5 дБ. Разумеется, более низкие требования лучше (требуется меньшая мощность, меньшая полоса). Вообще, более достоверным схемам соответствуют кривые, расположенные ближе к левой и нижней осям. Изучая кривые на рис. 3.14, видим, что биполярная схема имеет выигрыш в 3 дБ по сравнению с униполярной. Это Отличие могло быть предсказано ранее, поскольку отношение
порядка 12,5 дБ, а при биполярной передаче - не более 9,5 дБ. Разумеется, более низкие требования лучше (требуется меньшая мощность, меньшая полоса). Вообще, более достоверным схемам соответствуют кривые, расположенные ближе к левой и нижней осям. Изучая кривые на рис. 3.14, видим, что биполярная схема имеет выигрыш в 3 дБ по сравнению с униполярной. Это Отличие могло быть предсказано ранее, поскольку отношение ![]() в формулах (3.70) и (3.71) отличалось в 2 раза. В главе 4 будет показано, что при обнаружении с использованием согласованного фильтра полосовая антиподная передача сигналов (например, двоичная фазовая манипуляция) дает такое же значение
в формулах (3.70) и (3.71) отличалось в 2 раза. В главе 4 будет показано, что при обнаружении с использованием согласованного фильтра полосовая антиподная передача сигналов (например, двоичная фазовая манипуляция) дает такое же значение ![]() , как и узкополосная антиподная передача сигналов (например, с помощью биполярных импульсов). Также будет показано, что при обнаружении с помощью согласованного фильтра полосовая ортогональная передача сигналов (например, ортогональная частотная манипуляция) дает такое же значение
, как и узкополосная антиподная передача сигналов (например, с помощью биполярных импульсов). Также будет показано, что при обнаружении с помощью согласованного фильтра полосовая ортогональная передача сигналов (например, ортогональная частотная манипуляция) дает такое же значение ![]() , как и узкополосная ортогональная передача сигналов (например, с использованием униполярных импульсов).
, как и узкополосная ортогональная передача сигналов (например, с использованием униполярных импульсов).
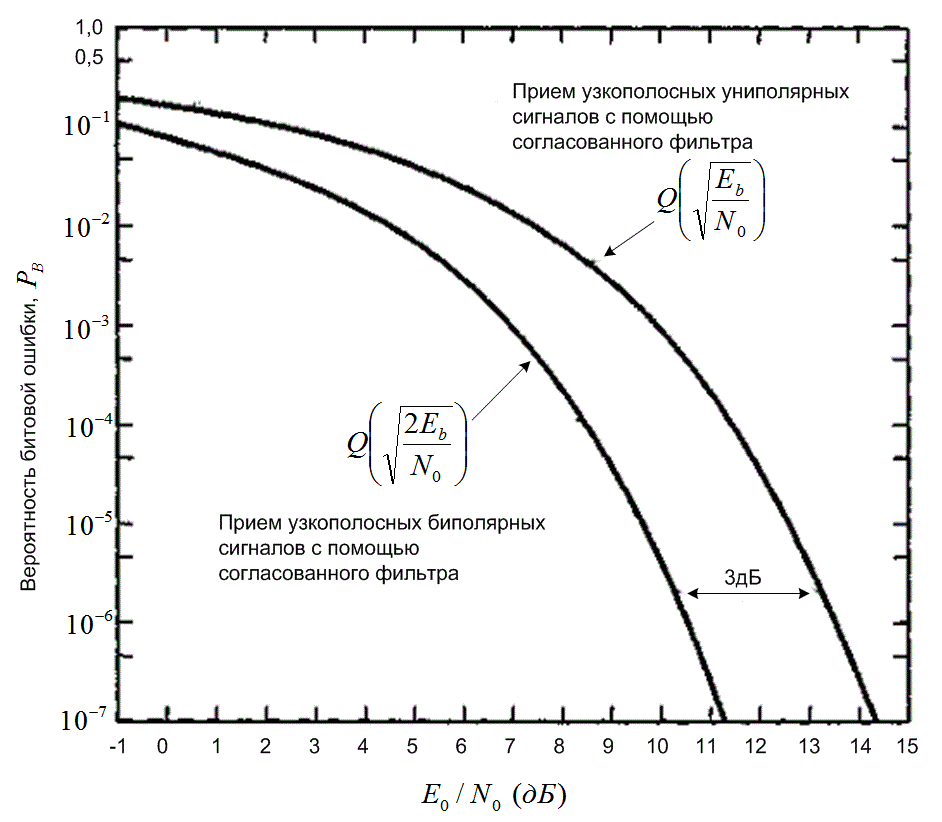
Рис.3.14. Вероятность появления ошибочного бита при униполярной и биполярной передаче сигналов
3.3. Межсимвольная интерференция
На рис. 3.15, а представлены фильтрующие элементы типичной системы цифровой связи. В системе - передатчике, приемнике и канале - используется множество разнообразных фильтров (и реактивных элементов, таких как емкость и индуктивность). В передатчике информационные символы, описываемые как импульсы или уровни напряжения, модулируют импульсы, которые затем фильтруются для согласования с определенными ограничениями полосы. В узкополосных системах канал (кабель) имеет распределенное реактивное сопротивление, искажающее импульсы. Некоторые полосовые системы, такие как беспроводные, являются, по сути, каналами с замираниями (см. главу 15), которые проявляют себя как нежелательные фильтры, также искажающие сигнал. Если принимающий фильтр настраивается на компенсацию искажения, вызванного как передатчиком, так и каналом, он зачастую называется выравнивающим (equalizing filter) или принимающим/выравнивающим (receiving/equalizing). На рис. 3.15, б приведена удобная модель системы, объединяющая все следствия фильтрации в одну общесистемную передаточную функцию.
![]() (3.77)
(3.77)
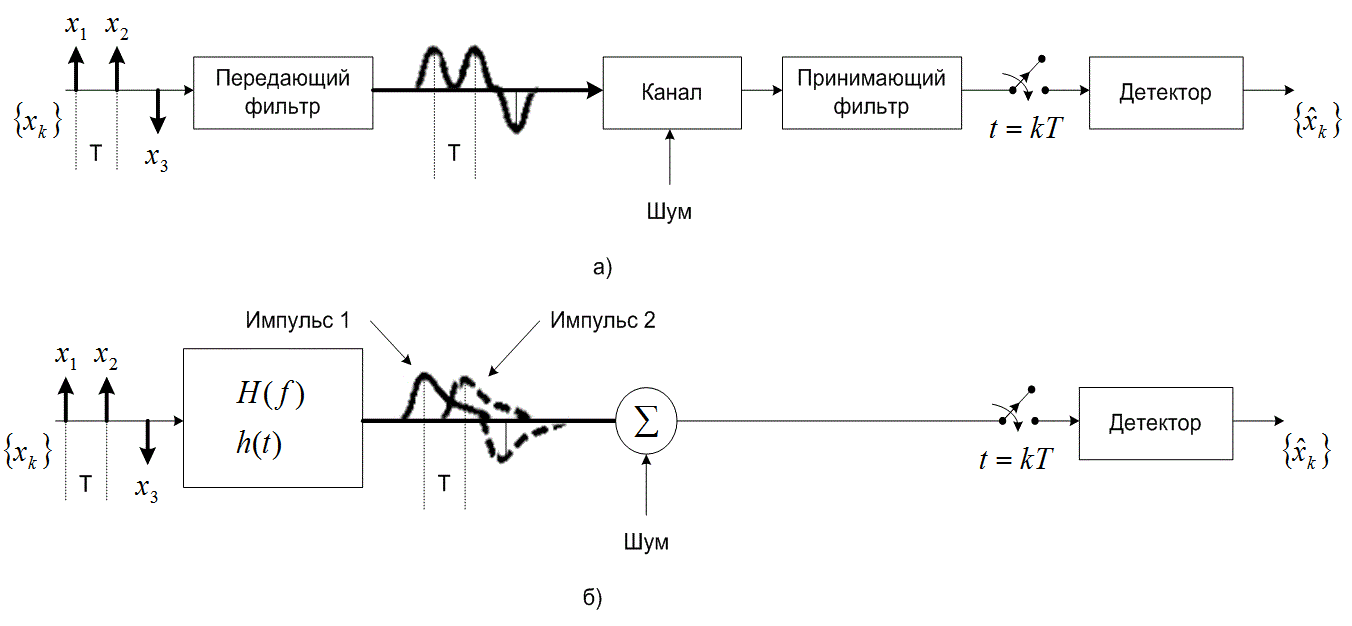
Рис.3.15. Межсимвольная интерференция в процессе обнаружения:
а) типичная узкополосная цифровая система; б) эквивалентная модель
Здесь ![]() характеризует передающий фильтр,
характеризует передающий фильтр, ![]() - фильтрацию в канале, а
- фильтрацию в канале, а ![]() - принимающий/выравнивающий фильтр. Таким образом, характеристика
- принимающий/выравнивающий фильтр. Таким образом, характеристика ![]() представляет передаточную функцию всей системы, отвечающую за все этапы фильтрации в различных местах цепочки передатчик-канал-приемник. В бинарной системе, использующей какую-нибудь распространенную кодировку РСМ, например NRZ-L, детектор принимает решение относительно значения символа путем сравнения выборки принятого импульса с порогом. Например, детектор, изображенный на рис. 3.15, решает, что была послана двоичная единица, если принятый импульс положителен, или двоичный нуль - в противном случае. Вследствие системной фильтрации принятые импульсы могут перекрываться, как показано на рис. 3.15, б. Хвост импульса может «размываться» на соседний интервал передачи символа, таким образом мешая процессу обнаружения и повышая вероятность появления ошибки; подобный процесс получил название межсимвольной интерференции (intersymbol interference - ISI). Даже при отсутствии шумов воздействие фильтрации и искажение, вызванное каналом, приводят к возникновению ISI. Иногда функция
представляет передаточную функцию всей системы, отвечающую за все этапы фильтрации в различных местах цепочки передатчик-канал-приемник. В бинарной системе, использующей какую-нибудь распространенную кодировку РСМ, например NRZ-L, детектор принимает решение относительно значения символа путем сравнения выборки принятого импульса с порогом. Например, детектор, изображенный на рис. 3.15, решает, что была послана двоичная единица, если принятый импульс положителен, или двоичный нуль - в противном случае. Вследствие системной фильтрации принятые импульсы могут перекрываться, как показано на рис. 3.15, б. Хвост импульса может «размываться» на соседний интервал передачи символа, таким образом мешая процессу обнаружения и повышая вероятность появления ошибки; подобный процесс получил название межсимвольной интерференции (intersymbol interference - ISI). Даже при отсутствии шумов воздействие фильтрации и искажение, вызванное каналом, приводят к возникновению ISI. Иногда функция ![]() задается, и задача состоит в определении
задается, и задача состоит в определении ![]() и
и ![]() , минимизирующих ISI на выходе
, минимизирующих ISI на выходе ![]() .
.
Исследованием проблемы задания формы принятого импульса с тем, чтобы предотвратить появление ISI на детекторе, долгое время занимался Найквист [6]. Он показал, что минимальная теоретическая ширина полосы системы, требуемая для определения ![]() символов/секунду без ISI, равна
символов/секунду без ISI, равна ![]() Гц. Это возможно, если передаточная функция системы
Гц. Это возможно, если передаточная функция системы ![]() имеет прямоугольную форму, как показано на рис. 3.16, а. Для узкополосных систем с такой
имеет прямоугольную форму, как показано на рис. 3.16, а. Для узкополосных систем с такой ![]() , что односторонняя ширина полосы фильтра равна 1/2T (идеальный фильтр Найквиста), импульсная характеристика функции
, что односторонняя ширина полосы фильтра равна 1/2T (идеальный фильтр Найквиста), импульсная характеристика функции ![]() , вычисляемая с помощью обратного преобразования Фурье (см. табл. А.1), имеет вид
, вычисляемая с помощью обратного преобразования Фурье (см. табл. А.1), имеет вид ![]() ; она показана на рис. 3.16, б. Импульс, описываемый функцией
; она показана на рис. 3.16, б. Импульс, описываемый функцией ![]() , называется идеальным импульсом Найквиста; он имеет бесконечную длительность и состоит из множественных лепестков: главного и боковых, именуемых хвостами. Найквист установил, что если каждый импульс принятой последовательности имеет вид
, называется идеальным импульсом Найквиста; он имеет бесконечную длительность и состоит из множественных лепестков: главного и боковых, именуемых хвостами. Найквист установил, что если каждый импульс принятой последовательности имеет вид ![]() , импульсы могут обнаруживаться без межсимвольной интерференции. На рис. 3.16, б показано, как удается обойти ISI. Итак, имеем два последовательных импульса,
, импульсы могут обнаруживаться без межсимвольной интерференции. На рис. 3.16, б показано, как удается обойти ISI. Итак, имеем два последовательных импульса, ![]() и
и ![]() . Несмотря на то что хвосты функции
. Несмотря на то что хвосты функции ![]() имеют бесконечную длительность, из рисунка видно, что в момент
имеют бесконечную длительность, из рисунка видно, что в момент ![]() взятия выборки функции
взятия выборки функции ![]() хвост функции
хвост функции ![]() проходит через точку нулевой амплитуды, и подобным образом он будет иметь нулевую амплитуду в моменты взятия выборок всех остальных импульсов последовательности
проходит через точку нулевой амплитуды, и подобным образом он будет иметь нулевую амплитуду в моменты взятия выборок всех остальных импульсов последовательности ![]() ,
, ![]() . Следовательно, предполагая идеальную синхронизацию процесса взятия выборок, получаем, что межсимвольная интерференция не будет влиять на процесс обнаружения. Чтобы узкополосная система могла обнаруживать 1/Т таких импульсов (символов) в секунду, ширина ее полосы должна быть равна 1/2T; другими словами, система с шириной полосы
. Следовательно, предполагая идеальную синхронизацию процесса взятия выборок, получаем, что межсимвольная интерференция не будет влиять на процесс обнаружения. Чтобы узкополосная система могла обнаруживать 1/Т таких импульсов (символов) в секунду, ширина ее полосы должна быть равна 1/2T; другими словами, система с шириной полосы ![]() Гц может поддерживать максимальную скорость передачи
Гц может поддерживать максимальную скорость передачи ![]() символов/с (ограничение полосы по Найквисту) без ISI. Следовательно, при идеальной фильтрации Найквиста (и нулевой межсимвольной интерференции) максимальная возможная скорость передачи символов на герц полосы, называемая уплотнением скорости передачи символов (symbol-rate packing), равна 2 символа/с/Гц. Вследствие прямоугольной формы передаточной функции идеального фильтра Найквиста и бесконечной длины соответствующего импульса, подобные идеальные фильтры нереализуемы; реализовать их можно только приближенно.
символов/с (ограничение полосы по Найквисту) без ISI. Следовательно, при идеальной фильтрации Найквиста (и нулевой межсимвольной интерференции) максимальная возможная скорость передачи символов на герц полосы, называемая уплотнением скорости передачи символов (symbol-rate packing), равна 2 символа/с/Гц. Вследствие прямоугольной формы передаточной функции идеального фильтра Найквиста и бесконечной длины соответствующего импульса, подобные идеальные фильтры нереализуемы; реализовать их можно только приближенно.
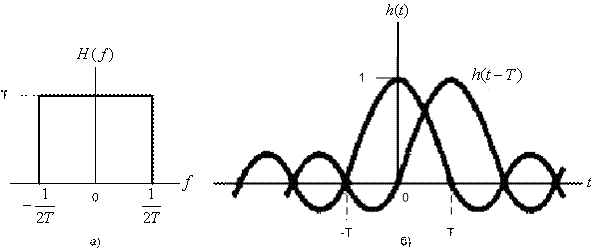
Рис. 3.16. Каналы Найквиста для нулевой межсимвольной интерференции:
а) прямоугольная передаточная функция системы ![]() ;
;
б) принятый импульс ![]()
Стоит отметить, что названия «фильтр Найквиста» и «импульс Найквиста» часто используются для описания обширного класса фильтраций и формообразований, удовлетворяющих условию нулевой межсимвольной интерференции в точках взятия выборок. Фильтр Найквиста - это фильтр, передаточная функция которого может быть представлена прямоугольной функцией, свернутой с любой четно-симметричной частотной функцией. Импульс Найквиста - это импульс, форма которого может быть описана функцией ![]() , умноженной на другую временную функцию. Следовательно, существует бесконечное множество фильтров Найквиста и соответствующих импульсов. В классе фильтров Найквиста наиболее популярными являются фильтры с характеристикой типа приподнятого косинуса или корня из приподнятого косинуса. Несколько позже эти фильтры будут рассмотрены подробно.
, умноженной на другую временную функцию. Следовательно, существует бесконечное множество фильтров Найквиста и соответствующих импульсов. В классе фильтров Найквиста наиболее популярными являются фильтры с характеристикой типа приподнятого косинуса или корня из приподнятого косинуса. Несколько позже эти фильтры будут рассмотрены подробно.
Основным параметром систем связи является эффективность использования полосы, ![]() , измеряемая в бит/с/Гц. Как можно понять из единиц измерения,
, измеряемая в бит/с/Гц. Как можно понять из единиц измерения, ![]() представляет меру скорости переноса данных на единицу ширины полосы, а значит, показывает, насколько эффективно любой метод передачи сигналов использует ресурс полосы. Поскольку ограничение ширины полосы по Найквисту устанавливает теоретическое максимальное уплотнение скорости передачи символов без межсимвольной интерференции, равное 2 символа/с/Гц, может возникнуть вопрос, можно ли что-то сказать об ограничении величин, измеряемых в бит/с/Гц. О последних ничего нельзя сказать прямо; ограничение связано только с импульсами или символами и возможностью обнаружения их амплитудных значений без искажения со стороны других импульсов. При нахождении
представляет меру скорости переноса данных на единицу ширины полосы, а значит, показывает, насколько эффективно любой метод передачи сигналов использует ресурс полосы. Поскольку ограничение ширины полосы по Найквисту устанавливает теоретическое максимальное уплотнение скорости передачи символов без межсимвольной интерференции, равное 2 символа/с/Гц, может возникнуть вопрос, можно ли что-то сказать об ограничении величин, измеряемых в бит/с/Гц. О последних ничего нельзя сказать прямо; ограничение связано только с импульсами или символами и возможностью обнаружения их амплитудных значений без искажения со стороны других импульсов. При нахождении ![]() для любой схемы передачи сигналов необходимо знать, сколько битов представляет каждый символ, что само по себе является темой отдельного рассмотрения. Допустим, сигналы кодируются с использованием М-уровневой кодировки РАМ. Каждый символ (включающий
для любой схемы передачи сигналов необходимо знать, сколько битов представляет каждый символ, что само по себе является темой отдельного рассмотрения. Допустим, сигналы кодируются с использованием М-уровневой кодировки РАМ. Каждый символ (включающий ![]() бит) представляется одной из М импульсных амплитуд. Для
бит) представляется одной из М импульсных амплитуд. Для ![]() бит на символ размер набора символов составляет
бит на символ размер набора символов составляет ![]() амплитуды. Таким образом, при 64-уровневой кодировке РАМ теоретическая максимальная эффективность использования полосы, не допускающая межсимвольной интерференции, равна 12 бит/с/Гц. (Подробнее об эффективности использования полосы в главе 9.)
амплитуды. Таким образом, при 64-уровневой кодировке РАМ теоретическая максимальная эффективность использования полосы, не допускающая межсимвольной интерференции, равна 12 бит/с/Гц. (Подробнее об эффективности использования полосы в главе 9.)
3.3.1. Формирование импульсов с целью снижения ISI
3.3.1.1. Цели и компромиссы
Чем компактнее спектр передачи сигналов, тем выше разрешенная скорость передачи данных или больше число пользователей, которые могут обслуживаться одновременно. Это имеет большое значение для поставщиков услуг связи, поскольку более эффективное использование доступной ширины полосы приносит больший доход. Для большинства систем связи (за исключением систем расширенного спектра, рассмотренных в главе 12) нашей задачей является максимальное сужение требуемой полосы системы. Найквист определил основное ограничение для такого сужения полосы. Но что произойдет, если заставить систему работать с меньшей полосой, чем определяется ограничением? Импульсы станут протяженнее по времени, что, вследствие увеличения межсимвольной интерференции, отрицательно скажется на достоверности передачи. Более разумным было бы сжатие полосы информационных импульсов до некоторого разумного значения, которое больше минимума, определенного Найквистом. Это выполняется путем формирования импульсов с помощью фильтра Найквиста. Если край полосы пропускания фильтра крутой, приблизительно соответствующий прямоугольной форме (рис. 3.16, а), то спектр сигнала можно сделать более компактным. В то же время использование подобного фильтра приводит к тому, что длительность импульсного отклика становится приблизительно равна бесконечности, как показано на рис. 3.16, б. Каждый импульс накладывается на все импульсы последовательности. Длительные отклики дают хвосты больших амплитуд около главного лепестка каждого импульса. Подобные хвосты нежелательны, поскольку, как видно из рис. 3.16, б, они вносят нулевую межсимвольную интерференцию только в том случае, если выборка производится точно в соответствующий момент времени; при больших хвостах даже небольшие ошибки синхронизации приведут к межсимвольной интерференции. Следовательно, хотя компактный спектр и позволяет оптимальным образом использовать полосу, он оказывается очень чувствительным к ошибкам синхронизации, приводящим к увеличению межсимвольной интерференции.
3.3.1.2. Фильтр с характеристикой типа приподнятого косинуса
Ранее говорилось, что принимающий фильтр часто называется выравнивающим, если он настраивается на компенсацию искажений, вносимых передатчиком и каналом. Другими словами, конфигурация этого фильтра выбрана так, чтобы оптимизировать общесистемную частотную передаточную функцию ![]() , описанную формулой (3.77). Одна из часто используемых передаточных функций
, описанную формулой (3.77). Одна из часто используемых передаточных функций ![]() принадлежит к классу функций Найквиста (нулевая ISI в моменты взятия выборок) и называется приподнятым косинусом (raised-cosine). Описывается эта функция следующим выражением.
принадлежит к классу функций Найквиста (нулевая ISI в моменты взятия выборок) и называется приподнятым косинусом (raised-cosine). Описывается эта функция следующим выражением.
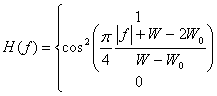
![]()
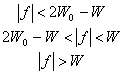 (3.78)
(3.78)
Здесь W - максимальная ширина полосы, a ![]() - минимальная ширина полосы по Найквисту для прямоугольного спектра и ширина полосы по уровню -6 дБ (или точка половинной амплитуды) для косинусоидального спектра. Разность
- минимальная ширина полосы по Найквисту для прямоугольного спектра и ширина полосы по уровню -6 дБ (или точка половинной амплитуды) для косинусоидального спектра. Разность ![]() называется «избытком полосы» (excess bandwidth); она означает дополнительную ширину полосы по сравнению с минимумом Найквиста (например, для прямоугольного спектра
называется «избытком полосы» (excess bandwidth); она означает дополнительную ширину полосы по сравнению с минимумом Найквиста (например, для прямоугольного спектра ![]() ). Коэффициент сглаживания (roll-off factor) определяется как
). Коэффициент сглаживания (roll-off factor) определяется как ![]() , где
, где ![]() . Коэффициент сглаживания - это избыток полосы, деленный на ширину полосы по уровню -6 дБ (т.е. относительный избыток полосы). Для данного
. Коэффициент сглаживания - это избыток полосы, деленный на ширину полосы по уровню -6 дБ (т.е. относительный избыток полосы). Для данного ![]() выравнивание
выравнивание ![]() задает требуемый избыток относительно
задает требуемый избыток относительно ![]() и характеризует крутизну фронта характеристики фильтра. На рис. 3.17, а для нескольких значений коэффициента сглаживания
и характеризует крутизну фронта характеристики фильтра. На рис. 3.17, а для нескольких значений коэффициента сглаживания ![]() (
(![]() ,
, ![]() и
и ![]() ) показана характеристика типа приподнятого косинуса. Случай
) показана характеристика типа приподнятого косинуса. Случай ![]() соответствует минимальной ширине полосы по Найквисту. Отметим, что при
соответствует минимальной ширине полосы по Найквисту. Отметим, что при ![]() требуемый избыток полосы равен 100% и хвосты характеристики достаточно малы. Система с подобной спектральной характеристикой может поддерживать скорость передачи символов
требуемый избыток полосы равен 100% и хвосты характеристики достаточно малы. Система с подобной спектральной характеристикой может поддерживать скорость передачи символов ![]() символов/с при использовании полосы в
символов/с при использовании полосы в ![]() , Гц (удвоенная минимальная полоса по Найквисту), что дает уплотнение скорости передачи, равное 1 символ/с/Гц. Импульсный отклик, соответствующий функции
, Гц (удвоенная минимальная полоса по Найквисту), что дает уплотнение скорости передачи, равное 1 символ/с/Гц. Импульсный отклик, соответствующий функции ![]() и определяемый выражением (3.78), равен следующему.
и определяемый выражением (3.78), равен следующему.
![]() (3.79)
(3.79)
Этот импульсный отклик изображен на рис. 3.17, б для ![]() ,
, ![]() и
и ![]() . Хвост имеет нулевые значения в каждый момент взятия выборки, вне зависимости от значения коэффициента сглаживания.
. Хвост имеет нулевые значения в каждый момент взятия выборки, вне зависимости от значения коэффициента сглаживания.
Фильтр, описанный уравнением (3.78), и импульс, представленный уравнением (3.79), можно реализовать только приблизительно, поскольку, строго говоря, спектр типа приподнятого косинуса физически не может быть реализован (причина та же, что и при реализации идеального фильтра Найквиста). Реализуемый фильтр должен иметь импульсный отклик конечной длительности и давать нулевой выход до момента включения импульса (см. раздел 1.7.2), что невозможно для семейства характеристик типа приподнятого косинуса. Эти нереализуемые фильтры являются непричинными (импульсный отклик фильтра имеет бесконечную продолжительность и фильтрованный импульс начинается в момент ![]() ). На практике фильтр формирования импульсов должен удовлетворять двум требованиям. Он должен обеспечивать желаемое сглаживание и должен быть реализуем (импульсный отклик должен усекаться до конечного размера).
). На практике фильтр формирования импульсов должен удовлетворять двум требованиям. Он должен обеспечивать желаемое сглаживание и должен быть реализуем (импульсный отклик должен усекаться до конечного размера).
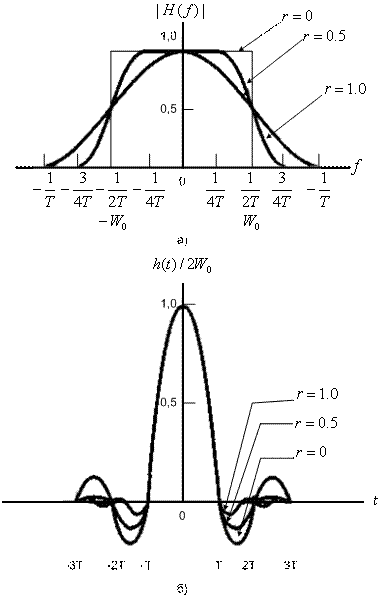
Рис. 3.17. Характеристики фильтров типа приподнятого косинуса:
а) передаточная функция системы; б) импульсный отклик системы
Используя ограничение ширины полосы по Найквисту (минимальная ширина полосы W, требуемая для поддержания скорости ![]() символов/с без межсимвольной интерференции, равна
символов/с без межсимвольной интерференции, равна ![]() Гц), можно вывести более общее соотношение между требуемой полосой и скоростью передачи символов, включающее коэффициент сглаживания
Гц), можно вывести более общее соотношение между требуемой полосой и скоростью передачи символов, включающее коэффициент сглаживания ![]() .
.
![]() (3.80)
(3.80)
Таким образом, при ![]() формула (3.80) описывает минимальную требуемую полосу для обеспечения идеальной фильтрации по Найквисту. При
формула (3.80) описывает минимальную требуемую полосу для обеспечения идеальной фильтрации по Найквисту. При ![]() ширина полосы превышает минимум Найквиста; следовательно, для этого случая
ширина полосы превышает минимум Найквиста; следовательно, для этого случая ![]() меньше удвоенной ширины полосы. Если демодулятор подает на выход одну выборку на символ, теорема о дискретном представлении Найквиста нарушается, поскольку у нас остается слишком мало выборок для однозначного восстановления аналогового сигнала (присутствует наложение). Впрочем, в системах цифровой связи нас и не интересует восстановление аналоговых сигналов. Кроме того, поскольку семейство фильтров с характеристикой типа приподнятого косинуса характеризуется нулевой межсимвольной Интерференцией в каждый момент произведения выборки из символа, мы по-прежнему можем добиться однозначного обнаружения.
меньше удвоенной ширины полосы. Если демодулятор подает на выход одну выборку на символ, теорема о дискретном представлении Найквиста нарушается, поскольку у нас остается слишком мало выборок для однозначного восстановления аналогового сигнала (присутствует наложение). Впрочем, в системах цифровой связи нас и не интересует восстановление аналоговых сигналов. Кроме того, поскольку семейство фильтров с характеристикой типа приподнятого косинуса характеризуется нулевой межсимвольной Интерференцией в каждый момент произведения выборки из символа, мы по-прежнему можем добиться однозначного обнаружения.
Сигналы с полосовой модуляцией (см. главу 4), такие как сигналы с амплитудной (amplitude-shift keying - ASK) и фазовой манипуляцией (phase-shift keying - PSK), требуют вдвое большей полосы передачи, чем эквивалентные узкополосные сигналы (см. раздел 1.7.1). Такие смещенные по частоте сигналы занимают полосу, вдвое большую по ширине соответствующей узкополосной; зачастую их называют двухполосными (double-sideband - DSB). Следовательно, для сигналов в кодировках ASK и PSK соотношение между требуемой шириной полосы ![]() и скоростью передачи символов
и скоростью передачи символов ![]() принимает следующий вид.
принимает следующий вид.
![]() (3.81)
(3.81)
Напомним, что передаточная функция, имеющая вид приподнятого косинуса, - это общесистемная функция ![]() , описывающая «полный проход» сообщения, отправленного передатчиком (в виде импульса), через канал и принимающий фильтр. Фильтрация в приемнике описывается частью общей передаточной функции, тогда как подавление межсимвольной интерференции обеспечивает передаточная функция, имеющая вид приподнятого косинуса. Как следствие сказанного, принимающий и передающий фильтры часто выбираются (согласовываются) так, чтобы передаточная функция каждого имела вид квадратного корня из приподнятого косинуса. Подавление любой межсимвольной интерференции, внесенной каналом, обеспечивает произведение этих двух функций, которое дает общую передаточную функцию системы, имеющую вид приподнятого косинуса. Если же для уменьшения последствий привнесенной каналом межсимвольной интерференции вводится отдельный выравнивающий фильтр, принимающий и выравнивающий фильтры могут совместно настраиваться так, чтобы компенсировать искажение, вызванное как передатчиком, так и каналом; при этом общая передаточная функция системы характеризуется нулевой межсимвольной интерференцией.
, описывающая «полный проход» сообщения, отправленного передатчиком (в виде импульса), через канал и принимающий фильтр. Фильтрация в приемнике описывается частью общей передаточной функции, тогда как подавление межсимвольной интерференции обеспечивает передаточная функция, имеющая вид приподнятого косинуса. Как следствие сказанного, принимающий и передающий фильтры часто выбираются (согласовываются) так, чтобы передаточная функция каждого имела вид квадратного корня из приподнятого косинуса. Подавление любой межсимвольной интерференции, внесенной каналом, обеспечивает произведение этих двух функций, которое дает общую передаточную функцию системы, имеющую вид приподнятого косинуса. Если же для уменьшения последствий привнесенной каналом межсимвольной интерференции вводится отдельный выравнивающий фильтр, принимающий и выравнивающий фильтры могут совместно настраиваться так, чтобы компенсировать искажение, вызванное как передатчиком, так и каналом; при этом общая передаточная функция системы характеризуется нулевой межсимвольной интерференцией.
Рассмотрим компромиссы, с которыми приходится сталкиваться при выборе фильтров формирования импульсов. Чем больше сглаживание фильтра, тем короче будут хвосты импульсов (из этого следует, что амплитуды хвостов также будут меньше). Меньшие хвосты менее чувствительны к ошибкам синхронизации, а значит, подвержены меньшему искажению вследствие межсимвольной интерференции. Отметим, что на рис. 3.17, б даже для ![]() ошибка синхронизации по-прежнему приводит к некоторому увеличению межсимвольной интерференции. Но в то же время в этом случае проблема менее серьезна, чем при
ошибка синхронизации по-прежнему приводит к некоторому увеличению межсимвольной интерференции. Но в то же время в этом случае проблема менее серьезна, чем при ![]() , поскольку при
, поскольку при ![]() хвосты сигнала
хвосты сигнала ![]() больше, чем при
больше, чем при ![]() . Увеличение хвостов - это плата за повышение избытка полосы. С другой стороны, чем меньше сглаживание фильтра, тем меньше избыток полосы, а это позволяет повысить скорость передачи сигналов или число пользователей, которые могут одновременно использовать систему. Э этом случае мы платим более длительными хвостами импульсов, большими их амплитудами, а следовательно, большей восприимчивостью к ошибкам синхронизации.
. Увеличение хвостов - это плата за повышение избытка полосы. С другой стороны, чем меньше сглаживание фильтра, тем меньше избыток полосы, а это позволяет повысить скорость передачи сигналов или число пользователей, которые могут одновременно использовать систему. Э этом случае мы платим более длительными хвостами импульсов, большими их амплитудами, а следовательно, большей восприимчивостью к ошибкам синхронизации.
3.3.2. Факторы роста вероятности ошибки
Факторы повышения вероятности возникновения ошибки в цифровой связи могут быть следующими. Во-первых, это связано с простым падением мощности принятого сигнала или с повышением мощности шума или интерференции, что в любом случае приводит к уменьшению отношения сигнал/шум, или ![]() . Во-вторых, это искажение сигнала, вызванное, например, межсимвольной интерференцией (intersymbol interference - ISI). Ниже показывается, чем отличаются эти факторы.
. Во-вторых, это искажение сигнала, вызванное, например, межсимвольной интерференцией (intersymbol interference - ISI). Ниже показывается, чем отличаются эти факторы.
Предположим, нам нужна система связи с такой зависимостью вероятности появления ошибочного бита ![]() от отношения
от отношения ![]() , какая изображена сплошной линией на рис. 3.18, а. Предположим, что после настройки системы и проведения измерений оказывается, к нашему разочарованию, что вероятность
, какая изображена сплошной линией на рис. 3.18, а. Предположим, что после настройки системы и проведения измерений оказывается, к нашему разочарованию, что вероятность ![]() соответствует не теоретической кривой, а кривой, показанной на рис. 3.18, а пунктиром. Причина снижения отношения
соответствует не теоретической кривой, а кривой, показанной на рис. 3.18, а пунктиром. Причина снижения отношения ![]() - потеря сигналом мощности или повышение шума или интерференции. Желаемой вероятности ошибочного бита в
- потеря сигналом мощности или повышение шума или интерференции. Желаемой вероятности ошибочного бита в ![]() соответствует теоретическая величина
соответствует теоретическая величина ![]() =10 дБ. Поскольку производительность реальной системы не соответствует теоретическим расчетам, нам следует использовать пунктирный график и добиться отношения
=10 дБ. Поскольку производительность реальной системы не соответствует теоретическим расчетам, нам следует использовать пунктирный график и добиться отношения ![]() , равного 12 дБ (для получения той же вероятности
, равного 12 дБ (для получения той же вероятности ![]() ). Если причины проблемы устранить нельзя, то насколько большее отношение
). Если причины проблемы устранить нельзя, то насколько большее отношение ![]() требуется теперь для получения необходимой вероятности ошибочного бита? Ответ, разумеется, - 2 дБ. Вообще, это может оказаться серьезной проблемой, особенно если система располагает ограниченной мощностью и получить дополнительные 2 дБ весьма сложно. Но все же уменьшение отношения
требуется теперь для получения необходимой вероятности ошибочного бита? Ответ, разумеется, - 2 дБ. Вообще, это может оказаться серьезной проблемой, особенно если система располагает ограниченной мощностью и получить дополнительные 2 дБ весьма сложно. Но все же уменьшение отношения ![]() не смертельно, по сравнению с ухудшением качества, вызванным искажением.
не смертельно, по сравнению с ухудшением качества, вызванным искажением.
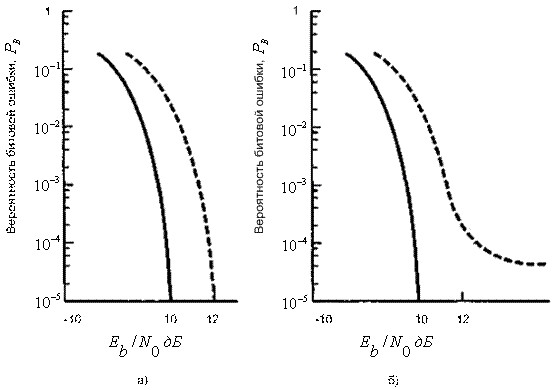
Рис. 3.18. Факторы роста вероятности ошибки: а) снижение ![]() ;
;
б) непреодолимое ухудшение, вызванное искажением
Обратимся к рис 3.18, б и представим, что мы снова не получили желаемой вероятности, описываемой сплошной кривой. Но в этот раз причиной стало не уменьшение отношения сигнал/шум, а искажение, вызванное межсимвольной интерференцией (реальная кривая показана пунктиром). Если причину проблемы устранить нельзя, то насколько большее отношение ![]() требуется теперь для получения необходимой вероятности ошибочного бита? В этом случае потребуется бесконечное увеличение. Другими словами, не существует такого
требуется теперь для получения необходимой вероятности ошибочного бита? В этом случае потребуется бесконечное увеличение. Другими словами, не существует такого ![]() , которое позволило бы устранить проблему. Если непреодолимое ухудшение описывается такой кривой, как показана на рис. 3.18, б, то никакое увеличение
, которое позволило бы устранить проблему. Если непреодолимое ухудшение описывается такой кривой, как показана на рис. 3.18, б, то никакое увеличение ![]() не может дать желаемого результата (предполагается, что нижняя точка пунктирной кривой находится выше требуемой вероятности
не может дать желаемого результата (предполагается, что нижняя точка пунктирной кривой находится выше требуемой вероятности ![]() ). Безусловно, каждая кривая зависимости
). Безусловно, каждая кривая зависимости ![]() от
от ![]() имеет где-то нижнюю точку, но если эта точка находится далеко за областью, представляющей практический интерес, то она уже не имеет значения.
имеет где-то нижнюю точку, но если эта точка находится далеко за областью, представляющей практический интерес, то она уже не имеет значения.
Итак, увеличение отношения ![]() не всегда помогает решить проблему межсимвольной интерференции (особенно если кривая зависимости
не всегда помогает решить проблему межсимвольной интерференции (особенно если кривая зависимости ![]() от
от ![]() выходит за область практического интереса). Это можно понять, взглянув на перекрывающиеся импульсы на рис. 3.15, б - увеличение отношения
выходит за область практического интереса). Это можно понять, взглянув на перекрывающиеся импульсы на рис. 3.15, б - увеличение отношения ![]() никак не влияет на длительность области перекрытия, и степень искажения импульсов не изменится. Так что же обычно противопоставляют искажающему эффекту межсимвольной интерференции? В данной ситуации наиболее приемлемым является метод, именуемый выравниванием (см. раздел 3.4). Поскольку причиной межсимвольной интерференции является искажение вследствие фильтрации в передатчике и канале, выравнивание можно рассматривать как процесс, компенсирующий подобные неоптимальные эффекты фильтрации.
никак не влияет на длительность области перекрытия, и степень искажения импульсов не изменится. Так что же обычно противопоставляют искажающему эффекту межсимвольной интерференции? В данной ситуации наиболее приемлемым является метод, именуемый выравниванием (см. раздел 3.4). Поскольку причиной межсимвольной интерференции является искажение вследствие фильтрации в передатчике и канале, выравнивание можно рассматривать как процесс, компенсирующий подобные неоптимальные эффекты фильтрации.
Пример 3.3. Требования к ширине полосы
а) Найдите минимальную ширину полосы, требуемую для узкополосной передачи последовательности четырехуровневых импульсов в кодировке РАМ со скоростью R=2400 бит/с, если передаточная характеристика системы имеет вид приподнятого косинуса со 100%-ным избытком полосы (![]() ).
).
б) Та же последовательность модулируется несущей, так что теперь узкополосный спектр смещен и центрирован на частоте ![]() . Определите минимальную двустороннюю полосу, требуемую для передачи модулированной последовательности РАМ. Передаточная характеристика считается такой же, как и в п. а.
. Определите минимальную двустороннюю полосу, требуемую для передачи модулированной последовательности РАМ. Передаточная характеристика считается такой же, как и в п. а.
Решение
а) ![]() , поскольку М=4 уровня, k=2.
, поскольку М=4 уровня, k=2.
Скорость передачи символов или импульсов ![]() символов /с;
символов /с;
минимальная ширина полосы ![]() Гц .
Гц .
На рис. 3.19, а во временной области показан принятый узкополосный импульс в кодировке РАМ; из выражения (3.79) получим функцию ![]() . На рис. 3.19, б показан Фурье-образ функции
. На рис. 3.19, б показан Фурье-образ функции ![]() - функция типа приподнятого косинуса. Отметим, что требуемая ширина полосы, W, находится в диапазоне от
- функция типа приподнятого косинуса. Отметим, что требуемая ширина полосы, W, находится в диапазоне от ![]() до
до ![]() ; она вдвое превышает теоретическую минимальную полосу по Найквисту.
; она вдвое превышает теоретическую минимальную полосу по Найквисту.
б) Здесь, как и в п. а,
![]() символов/с;
символов/с;
![]() Гц.
Гц.
На рис. 3.20, а показан модулированный принятый импульс. Этот сигнал в кодировке РАМ можно рассматривать как произведение высокочастотной синусоидальной несущей и сигнала с формой импульса, показанной на рис. 3.19, а. Односторонний спектральный график на рис. 3.20, б показывает модулированный сигнал, полоса которого выражается следующей формулой.
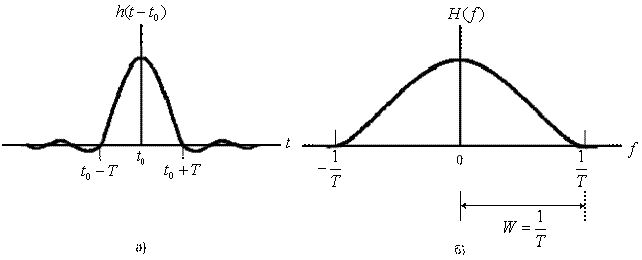
Рис. 3.19. Сформированный импульс и узкополосный спектр типа приподнятого косинуса
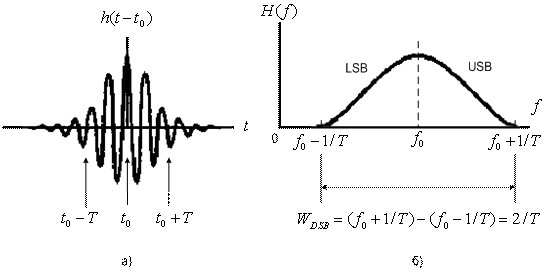
Рис.3.20. Модулированный сформулированный импульс и двухполосный модулированный спектр типа приподнятого косинуса
При смещении вверх по частоте спектра, показанного на рис. 3.19, а, смещаются отрицательная и положительная половины узкополосного спектра, таким образом требуемая полоса передачи дублируется. Как указывает название, двусторонний сигнал имеет две боковые полосы: верхнюю боковую полосу (upper sideband - USB), получаемую из положительной половины узкополосного сигнала, и нижнюю боковую полосу (lower sideband - LSB), получаемую из отрицательной половины.
Пример 3.4. Цифровые телефонные каналы
Сравните требования к ширине полосы системы для наземного аналогового телефонного канала передачи в речевом диапазоне (3 кГц) и цифрового канала. Для цифрового канала речь форматируется как поток битов в кодировке РСМ с частотой дискретизации аналогового сигнала 8000 выборок/с. Каждая речевая выборка квантуется на один из 256 уровней. Затем поток битов передается с использованием сигналов РСМ и принимается с нулевой межсимвольной интерференцией.
Решение
Процесс дискретизации и квантования дает слова РСМ, каждое из которых представляет одну выборку и относится к одному из L=256 различных уровней. Если каждая выборка передается как 256-уровневый импульс (символ) в кодировке РАМ, то из формулы (3.82) получим ширину полосы (без межсимвольной интерференции), требуемую для передачи ![]() символов/с.
символов/с.
![]() Гц
Гц
Здесь равенство достигается только при использовании идеальной фильтрации Найквиста. Поскольку цифровая телефонная система использует (двоичные) сигналы РСМ, каждое слово РСМ преобразовывается в ![]() бит. Следовательно, полоса, необходимая для передачи речи с использованием РСМ, равна следующему выражению.
бит. Следовательно, полоса, необходимая для передачи речи с использованием РСМ, равна следующему выражению.
![]()
Описанный аналоговый канал передачи речи (3 кГц) обычно требует полосы порядка 4 кГц, включая некоторые разделительные полосы между каналами, называемые защитными (guard band). Следовательно, при использовании формата РСМ, 8-битового квантования и двоичной передачи с сигналами РСМ требуется примерно в 8 раз большая полоса, чем при использовании аналогового канала.
3.3.3. Демодуляция/обнаружение сформированных импульсов
3.3.3.1. Согласованные и обычные фильтры
Обычные фильтры отсекают нежелательные спектральные компоненты принятого сигнала при поддержании некоторой точности воспроизведения сигналов в выбранной области спектра, называемой полосой пропускания (pass-band). В общем случае эти фильтры разрабатываются для обеспечения приблизительно одинакового усиления, их характеристика дает линейное увеличение фазы в зависимости от частоты в пределах полосы пропускания и минимальное поглощение в остальной части спектра, именуемой полосой заграждения (stop-band). Согласованный фильтр имеет несколько иные «проектные приоритеты», направленные на максимизацию отношения SNR известного сигнала при шуме AWGN. В обычных фильтрах используются случайные сигналы, и результат фильтрации определяется только полосами сигналов, тогда как согласованные фильтры применяются с известными сигналами, имеющими произвольные параметры (такие, как амплитуда и время). Согласованный фильтр можно рассматривать как шаблон, который согласовывает обрабатываемый сигнал с известной формой. Обычный фильтр сохраняет временного или спектральную структуру сигнала. Согласованный фильтр, наоборот, в значительной степени модифицирует временную структуру путем сбора энергии сигнала, которая согласовывается с его шаблоном, и в завершение каждого интервала передачи символа представляет результат фильтрации в виде значения максимальной амплитуды. Вообще, в цифровой связи приемник обрабатывает поступающие сигналы с помощью фильтров обоих типов. Задачей обычного фильтра является изоляция и извлечение высокоточной аппроксимации сигнала с последующей передачей результата согласованному фильтру. Согласованный фильтр накапливает энергию принятого сигнала, и в момент взятия выборки ![]() на выход фильтра подается напряжение, пропорциональное этой энергии, после чего следует обнаружение и дальнейшая обработка сигнала.
на выход фильтра подается напряжение, пропорциональное этой энергии, после чего следует обнаружение и дальнейшая обработка сигнала.
3.3.3.2. Импульсы Найквиста
Рассмотрим последовательность информационных импульсов на входе передатчика и последовательность импульсов, получаемую на выходе согласованного фильтра с характеристикой типа приподнятого косинуса (перед дискретизацией). На рис. 3.21 переданные данные представлены импульсными сигналами, которые появляются в моменты времени ![]() . Фильтрование приводит к расширению входящих сигналов, а следовательно, к запаздыванию их во времени. Время поступления импульсов обозначим
. Фильтрование приводит к расширению входящих сигналов, а следовательно, к запаздыванию их во времени. Время поступления импульсов обозначим ![]() . Импульс, переданный в момент времени
. Импульс, переданный в момент времени ![]() . поступает в приемник в момент времени
. поступает в приемник в момент времени ![]() . Хвост, предшествующий основному лепестку демодулированного импульса, называется его предтечей (precursor). Для реальной системы с заданным системным эталонным временем принцип причинности дает условие
. Хвост, предшествующий основному лепестку демодулированного импульса, называется его предтечей (precursor). Для реальной системы с заданным системным эталонным временем принцип причинности дает условие ![]() , а разность времен
, а разность времен ![]() выражает задержку распространения в системе. В данном примере интервал времени от начала предтечи демодулированного импульса и до появления его главного лепестку или максимальной амплитуды равен 3T (утроенное время передачи импульса). Каждый выходящий импульс последовательности накладывается на другие импульсы; каждый импульс воздействует на основные лепестки трех предшествующих и трех последующих импульсов. В подобном случае, когда импульс фильтруется (формируется) так, что занимает более одного интервала передачи символа, определяется параметр, называемый временем поддержки (support time) импульса. Время поддержки - это количество интервалов передачи символа в течение длительности импульса. На рис. 3.21 время поддержки импульса равно 6 интервалам передачи символа (7 информационных точек с 6 интервалами между ними).
выражает задержку распространения в системе. В данном примере интервал времени от начала предтечи демодулированного импульса и до появления его главного лепестку или максимальной амплитуды равен 3T (утроенное время передачи импульса). Каждый выходящий импульс последовательности накладывается на другие импульсы; каждый импульс воздействует на основные лепестки трех предшествующих и трех последующих импульсов. В подобном случае, когда импульс фильтруется (формируется) так, что занимает более одного интервала передачи символа, определяется параметр, называемый временем поддержки (support time) импульса. Время поддержки - это количество интервалов передачи символа в течение длительности импульса. На рис. 3.21 время поддержки импульса равно 6 интервалам передачи символа (7 информационных точек с 6 интервалами между ними).
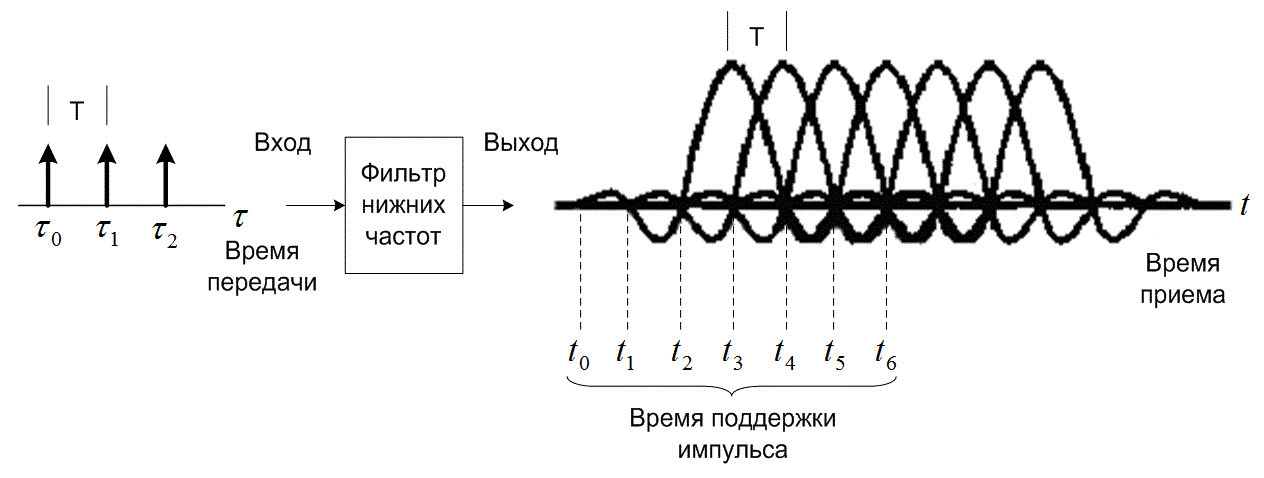
Рис. 3.21. Фильтрованная последовательность импульсов: выход и вход
На рис. 3.22, а показан импульсный отклик фильтра с характеристикой типа корня из приподнятого косинуса (максимальное значение нормированного фильтра равно единице, сглаживание фильтра ![]() ), а на рис. 3.22, б изображен импульсный отклик фильтра с характеристикой типа приподнятого косинуса, называемый импульсом Найквиста (нормирование и значение коэффициента сглаживания такие же, как и на рис. 3.22, а). Изучая эти два импульса, можно заметить, что они очень похожи. Однако первый имеет несколько более быстрые переходы, а значит, его спектр (корень квадратный из приподнятого косинуса) не так быстро затухает, как спектр (приподнятый косинус) импульса Найквиста. Еще одним малозаметным, но важным отличием является то, что импульс Найквиста с характеристикой типа корня из приподнятого косинуса не дает нулевой межсимвольной интерференции (можно проверить, что хвосты импульса на рис. 3.22, а не проходят через точку нулевой амплитуды в моменты взятия выборок). В то же время, если фильтр с характеристикой типа корня из приподнятого косинуса используется и в передатчике, и в приемнике, произведение передаточных функций двух фильтров дает характеристику типа приподнятого косинуса, что означает нулевую межсимвольную интерференцию на выходе.
), а на рис. 3.22, б изображен импульсный отклик фильтра с характеристикой типа приподнятого косинуса, называемый импульсом Найквиста (нормирование и значение коэффициента сглаживания такие же, как и на рис. 3.22, а). Изучая эти два импульса, можно заметить, что они очень похожи. Однако первый имеет несколько более быстрые переходы, а значит, его спектр (корень квадратный из приподнятого косинуса) не так быстро затухает, как спектр (приподнятый косинус) импульса Найквиста. Еще одним малозаметным, но важным отличием является то, что импульс Найквиста с характеристикой типа корня из приподнятого косинуса не дает нулевой межсимвольной интерференции (можно проверить, что хвосты импульса на рис. 3.22, а не проходят через точку нулевой амплитуды в моменты взятия выборок). В то же время, если фильтр с характеристикой типа корня из приподнятого косинуса используется и в передатчике, и в приемнике, произведение передаточных функций двух фильтров дает характеристику типа приподнятого косинуса, что означает нулевую межсимвольную интерференцию на выходе.
Было бы неплохо рассмотреть, как импульсы Найквиста с характеристикой типа корня из приподнятого косинуса выглядят на выходе передатчика и какую форму они имеют после демодуляции на согласованном фильтре, характеристика которого также представляет собой корень из приподнятого косинуса.
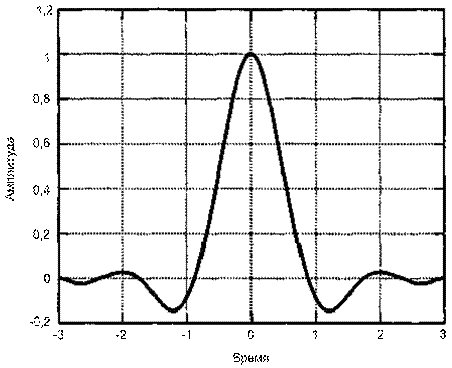
Рис. 3.22, а. Импульс Найквиста с характеристикой типа корня
из приподнятого косинуса
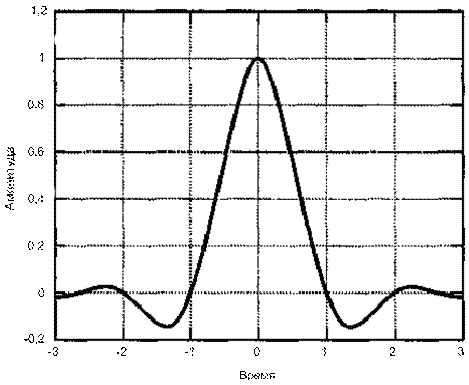
Рис. 3.22, б. Импульс Найквиста с характеристикой типа
приподнятого косинуса
На рис. 3.23, а в качестве примера передачи приведена последовательность символов сообщения ![]() из четверичного набора символов, где алфавит состоит из символов
из четверичного набора символов, где алфавит состоит из символов ![]() . Будем считать, что импульсы модулируются с помощью четверичной кодировки РАМ, а их форма определяется фильтром с характеристикой типа корня из приподнятого косинуса с коэффициентом сглаживания
. Будем считать, что импульсы модулируются с помощью четверичной кодировки РАМ, а их форма определяется фильтром с характеристикой типа корня из приподнятого косинуса с коэффициентом сглаживания ![]() . Аналоговый сигнал на рис. 3.23, а описывает выход передатчика. Сигнал на выходе (последовательность импульсов Найквиста, форма которых получена с выхода фильтра с характеристикой типа корня из приподнятого косинуса) запаздывает относительно сигнала на входе (показанного в виде импульсов), но для удобства визуального представления, чтобы читатель мог сравнить выход фильтра с его входом, оба сигнала изображены как одновременные. В действительности передается (или модулируется) только аналоговый сигнал.
. Аналоговый сигнал на рис. 3.23, а описывает выход передатчика. Сигнал на выходе (последовательность импульсов Найквиста, форма которых получена с выхода фильтра с характеристикой типа корня из приподнятого косинуса) запаздывает относительно сигнала на входе (показанного в виде импульсов), но для удобства визуального представления, чтобы читатель мог сравнить выход фильтра с его входом, оба сигнала изображены как одновременные. В действительности передается (или модулируется) только аналоговый сигнал.
На рис. 3.23, б показаны те же задержанные символы сообщения, а также сигнал с выхода согласованного фильтра с характеристикой типа корня из приподнятого косинуса, что для всей системы в сумме дает передаточную функцию типа приподнятого косинуса.
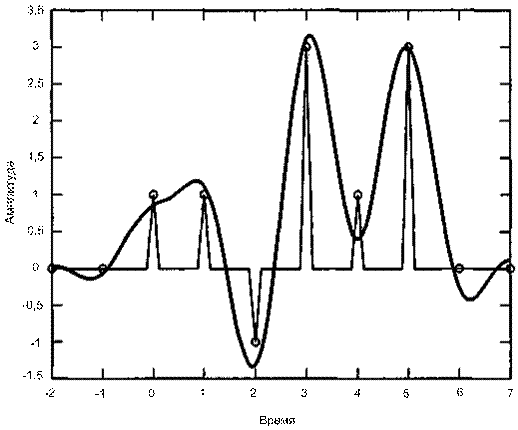
Рис. 3.23, а. М-уровневый сигнал Найквиста, пропущенный через фильтр с характеристикой типа корня из приподнятого косинуса, и входные дискретные значения, задержанные на некоторое время
Существует простой тест, позволяющий проверить, содержит ли фильтрованный сигнал с выхода межсимвольную интерференцию (предполагается отсутствие шума). Для этого требуется всего лишь произвести выборку фильтрованного сигнала в моменты времени, соответствующие исходным входящим выборкам; если полученные сигналы в результате выборки не отличаются от выборок исходного сообщения, то сигналы с выхода фильтра имеют нулевую межсимвольную интерференцию (в моменты взятия выборок). При сравнении рис. 3.23, а и 3.23, б на предмет межсимвольной интерференции видно, что дискретизация сигнала Найквиста на рис. 3.23, а (выход передатчика) не дает точных исходных выборок; в то же время дискретизация сигнала Найквиста на рис. 3.23, б (выход согласованного фильтра) дает точные исходные выборки. Это еще раз подтверждает, что фильтр Найквиста дает нулевую межсимвольную интерференцию в моменты взятия выборок, тогда как другие фильтры не имеют такой особенности.
3.4. Выравнивание
3.4.1. Характеристики канала
Многие каналы связи (например, телефонные или беспроводные) можно охарактеризовать как узкополосные линейные фильтры с импульсной характеристикой ![]() и частотной характеристикой
и частотной характеристикой
![]() (3.82)
(3.82)
где ![]() и
и ![]() - Фурье-образы друг друга,
- Фурье-образы друг друга, ![]() - амплитудная характеристика канала, a
- амплитудная характеристика канала, a ![]() - фазовая характеристика канала.
- фазовая характеристика канала.
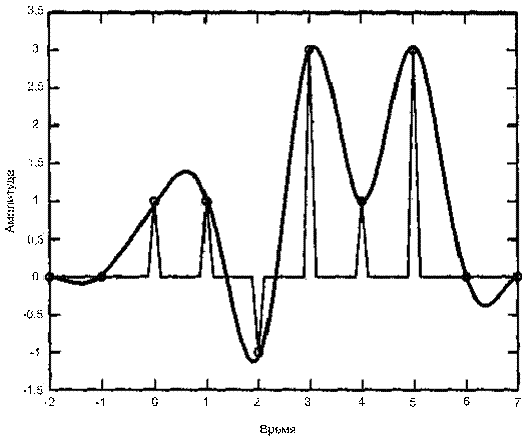
Рис. 3.23, б. Выход фильтра с характеристикой типа приподнятого косинуса и входные дискретные значения, задержанные на некоторое время
В разделе 1.6.3 было показано, что для получения идеальных (неискажающих) передающих характеристик канала в пределах полосы сигнала W, функция ![]() должна быть константой. Кроме того,
должна быть константой. Кроме того, ![]() должна быть линейной функцией частоты, что эквивалентно утверждению «запаздывание должно быть постоянным для всех спектральных компонентов сигнала». Если
должна быть линейной функцией частоты, что эквивалентно утверждению «запаздывание должно быть постоянным для всех спектральных компонентов сигнала». Если ![]() не является константой в пределах полосы W, то канал будет искажать амплитуду сигнала. Если
не является константой в пределах полосы W, то канал будет искажать амплитуду сигнала. Если ![]() не является линейной функцией частоты в пределах полосы W, канал будет искажать фазу. Во многих каналах, искажающих подобным образом информацию, например каналах с замираниями, искажение фазы и амплитуды обычно проявляется одновременно. При передаче последовательности импульсов подобное искажение проявляется в виде рассеивания или «размывания» импульсов, так что ни один импульс принятой демодулированной последовательности не определяется однозначно. В разделе 3.3 описывалось перекрытие импульсов, известное как межсимвольная интерференция (intersymbol interference - ISI). Это эффект, который проявляется в большинстве систем модуляции и является одной из основных помех надежной высокоскоростной передачи по узкополосным каналам. Совокупность методов обработки или фильтрации сигнала, направленных на устранение или снижение межсимвольной интерференции, именуется как «выравнивание» (equalization) и рассматривается в данном разделе.
не является линейной функцией частоты в пределах полосы W, канал будет искажать фазу. Во многих каналах, искажающих подобным образом информацию, например каналах с замираниями, искажение фазы и амплитуды обычно проявляется одновременно. При передаче последовательности импульсов подобное искажение проявляется в виде рассеивания или «размывания» импульсов, так что ни один импульс принятой демодулированной последовательности не определяется однозначно. В разделе 3.3 описывалось перекрытие импульсов, известное как межсимвольная интерференция (intersymbol interference - ISI). Это эффект, который проявляется в большинстве систем модуляции и является одной из основных помех надежной высокоскоростной передачи по узкополосным каналам. Совокупность методов обработки или фильтрации сигнала, направленных на устранение или снижение межсимвольной интерференции, именуется как «выравнивание» (equalization) и рассматривается в данном разделе.
На рис. 2.1 выравнивание разбито на две большие категории. Первая категория, оценка последовательности с максимальным правдоподобием (maximum-likelihood sequence estimation - MLSE), подразумевает измерение ![]() с последующей подстройкой приемника под среду передачи. Цель такой подстройки - позволить детектору произвести точную оценку демодулированной искаженной последовательности импульсов. При использовании приемника MLSE искаженные выборки не изменяются и не проходят этап непосредственной компенсации последствий помех; вместо этого приемник перенастраивается так, чтобы максимально эффективно работать с искаженными выборками. (Пример этого метода, известный как выравнивание Витерби, рассмотрен в разделе 15.7.1.) Вторая категория, выравнивание с помощью фильтров, включает использование фильтров для компенсации искажения импульсов. В этом случае детектору предоставляется последовательность демодулированных выборок, модифицированных или «очищенных» эквалайзером от последствий ISI. Выравнивание с помощью фильтров (более популярный подход из двух описанных выше) также имеет несколько подтипов. Фильтры могут быть линейными устройствами, содержащими только элементы с прямой связью (трансверсальные эквалайзеры), или нелинейными, включающими элементы с обратной связью (эквалайзеры с решающей обратной связью). Кроме того, фильтры могут различаться алгоритмом работы, который может быть заданным или адаптивным. Также они могут различаться разрешением или частотой обновления. Если выборки производятся только в пределах символа, т.е. одна выборка на символ, то это символьное разделение. Если каждому символу соответствует несколько выборок, то это фракционное разделение.
с последующей подстройкой приемника под среду передачи. Цель такой подстройки - позволить детектору произвести точную оценку демодулированной искаженной последовательности импульсов. При использовании приемника MLSE искаженные выборки не изменяются и не проходят этап непосредственной компенсации последствий помех; вместо этого приемник перенастраивается так, чтобы максимально эффективно работать с искаженными выборками. (Пример этого метода, известный как выравнивание Витерби, рассмотрен в разделе 15.7.1.) Вторая категория, выравнивание с помощью фильтров, включает использование фильтров для компенсации искажения импульсов. В этом случае детектору предоставляется последовательность демодулированных выборок, модифицированных или «очищенных» эквалайзером от последствий ISI. Выравнивание с помощью фильтров (более популярный подход из двух описанных выше) также имеет несколько подтипов. Фильтры могут быть линейными устройствами, содержащими только элементы с прямой связью (трансверсальные эквалайзеры), или нелинейными, включающими элементы с обратной связью (эквалайзеры с решающей обратной связью). Кроме того, фильтры могут различаться алгоритмом работы, который может быть заданным или адаптивным. Также они могут различаться разрешением или частотой обновления. Если выборки производятся только в пределах символа, т.е. одна выборка на символ, то это символьное разделение. Если каждому символу соответствует несколько выборок, то это фракционное разделение.
Модифицируем уравнение (3.77), заменив принимающий/ выравнивающий фильтр отдельными (принимающим и выравнивающим) фильтрами, определяемыми частотными передаточными функциями ![]() и
и ![]() . Будем также считать, что общая передаточная функция системы
. Будем также считать, что общая передаточная функция системы ![]() имеет вид приподнятого косинуса (raised-cosine), и обозначим ее
имеет вид приподнятого косинуса (raised-cosine), и обозначим ее ![]() . Таким образом, можем записать следующее.
. Таким образом, можем записать следующее.
![]() (3.83)
(3.83)
В системах, представляющих практический интерес, частотная передаточная функция системы ![]() и ее импульсная характеристика
и ее импульсная характеристика ![]() не известны с точностью, достаточной для разработки приемника, который в любой момент времени дает нулевую межсимвольную интерференцию. Передающий и принимающий фильтры, как правило, выбираются так, чтобы
не известны с точностью, достаточной для разработки приемника, который в любой момент времени дает нулевую межсимвольную интерференцию. Передающий и принимающий фильтры, как правило, выбираются так, чтобы
![]() (3.84)
(3.84)
Таким образом, характеристики ![]() и
и ![]() имеют вид корней из приподнятого косинуса. Следовательно, передаточная функция эквалайзера, необходимая для компенсации искажения, внесенного каналом, является обратной передаточной функции канала.
имеют вид корней из приподнятого косинуса. Следовательно, передаточная функция эквалайзера, необходимая для компенсации искажения, внесенного каналом, является обратной передаточной функции канала.
![]() (3.85)
(3.85)
Иногда частотная передаточная функция системы допускает мёжсимвольную интерференцию в специально выбранных точках дискретизации (например, передаточная функция гауссового фильтра). Такие передаточные функции позволяют повысить эффективность использования полосы, по сравнению с фильтром с характеристикой типа приподнятого косинуса. При выборе такого конструкторского решения выравнивающий фильтр должен компенсировать не только внесенную каналом межсимвольную интерференцию, но и ISI, внесенную передающим и принимающим фильтрами [7].
3.4.2. Глазковая диаграмма
Глазковая диаграмма - это изображение, полученное в результате измерения отклика системы на заданные узкополосные сигналы. На вертикальные пластины осциллографа подается отклик приемника на случайную последовательность импульса, а на горизонтальные - пилообразный сигнал сигнальной частоты. Другими словами, горизонтальная временная развертка осциллографа устанавливается равной длительности символа (импульса). В течение каждого сигнального промежутка очередной сигнал накладывается на семейство кривых в интервале ![]() . На рис. 3.24 приведена глазковая диаграмма, получаемая при двоичной антиподной (биполярные импульсы) передаче сигналов. Поскольку символы поступают из случайного источника, они могут быть как положительными, так и отрицательными, и отображение послесвечения электронного луча позволяет видеть изображение, имеющее форму глаза. Ширина открытия глаза указывает время, в течение которого должна быть произведена выборка сигнала. Разумеется, оптимальное время взятия выборки соответствует максимально распахнутому глазу, что дает максимальную защиту от воздействия помех. Если в системе не используется фильтрация, т.е. если передаваемым информационным импульсам соответствует бесконечная полоса, то отклик системы дает импульсы идеальной прямоугольной формы. В этом случае диаграмма будет выглядеть уже не как глаз, а как прямоугольник. Диапазон разностей амплитуд, обозначенный через
. На рис. 3.24 приведена глазковая диаграмма, получаемая при двоичной антиподной (биполярные импульсы) передаче сигналов. Поскольку символы поступают из случайного источника, они могут быть как положительными, так и отрицательными, и отображение послесвечения электронного луча позволяет видеть изображение, имеющее форму глаза. Ширина открытия глаза указывает время, в течение которого должна быть произведена выборка сигнала. Разумеется, оптимальное время взятия выборки соответствует максимально распахнутому глазу, что дает максимальную защиту от воздействия помех. Если в системе не используется фильтрация, т.е. если передаваемым информационным импульсам соответствует бесконечная полоса, то отклик системы дает импульсы идеальной прямоугольной формы. В этом случае диаграмма будет выглядеть уже не как глаз, а как прямоугольник. Диапазон разностей амплитуд, обозначенный через ![]() , является мерой искажения, вызванного межсимвольной интерференцией, а диапазон разностей времен перехода через нуль, обозначенный через
, является мерой искажения, вызванного межсимвольной интерференцией, а диапазон разностей времен перехода через нуль, обозначенный через ![]() , есть мерой неустойчивой синхронизации. На рисунке также показана мера запаса помехоустойчивости
, есть мерой неустойчивой синхронизации. На рисунке также показана мера запаса помехоустойчивости ![]() и чувствительность к ошибкам синхронизации
и чувствительность к ошибкам синхронизации ![]() . Чаще всего глазковая диаграмма используется для качественной оценки степени межсимвольной интерференции. По мере закрытия глаза ISI увеличивается, а по мере открытия - уменьшается.
. Чаще всего глазковая диаграмма используется для качественной оценки степени межсимвольной интерференции. По мере закрытия глаза ISI увеличивается, а по мере открытия - уменьшается.
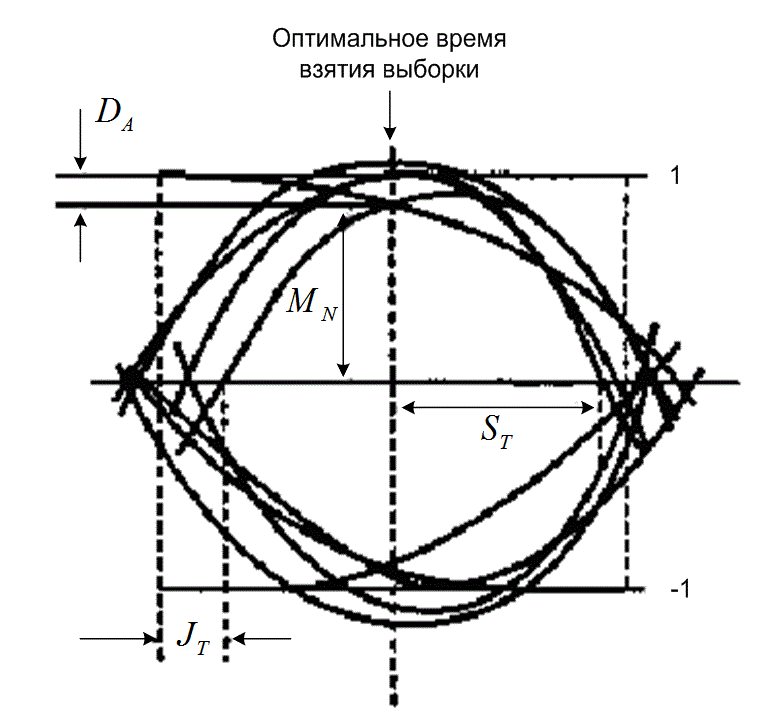
Рис. 3.24. Глазковая диаграмма
3.4.3. Типы эквалайзеров
3.4.3.1. Трансверсальный эквалайзер
В качестве тестовой последовательности, используемой для выравнивания, часто выбирается шумоподобная последовательность с широкополосным спектром, с помощью которой оценивается отклик канала. В простейшем смысле настройка может заключаться в передаче простого короткого импульса (приблизительно, идеального импульса) с последующим изучением импульсного отклика канала. На практике в качестве тестовой последовательности предпочтителен не единичный импульс, а псевдошумовой сигнал, поскольку последний имеет большую среднюю мощность, а значит, большее отношение сигнал/шум при одинаковых максимальных переданных мощностях. Для изучения трансверсального фильтра предположим, что через систему был передан единственный импульс, причем система спроектирована таким образом, что общая передаточная функция имеет вид приподнятого косинуса ![]() . Также будем считать, что канал вводит межсимвольную интерференцию, так что принятый демодулированный импульс искажается, как показано на рис. 3.25, поэтому боковые лепестки, ближайшие к главному лепестку импульса, не проходят через нуль в моменты взятия выборок. Искажение можно рассматривать как положительное или отрицательное отражение, появляющееся до и после главного лепестка. Для получения желаемой передаточной функции с характеристикой типа приподнятого косинуса выравнивающий фильтр, как следует из уравнения (3.85), должен иметь частотный отклик
. Также будем считать, что канал вводит межсимвольную интерференцию, так что принятый демодулированный импульс искажается, как показано на рис. 3.25, поэтому боковые лепестки, ближайшие к главному лепестку импульса, не проходят через нуль в моменты взятия выборок. Искажение можно рассматривать как положительное или отрицательное отражение, появляющееся до и после главного лепестка. Для получения желаемой передаточной функции с характеристикой типа приподнятого косинуса выравнивающий фильтр, как следует из уравнения (3.85), должен иметь частотный отклик ![]() , тогда отклик канала при умножении на
, тогда отклик канала при умножении на ![]() будет
будет ![]() . Другими словами, мы хотим, чтобы выравнивающий фильтр вырабатывал набор подавляющих отражений. Поскольку нас интересуют выборки выровненного сигнала только в определенные моменты времени, проектирование подобного выравнивающего фильтра может быть довольно простой задачей.
. Другими словами, мы хотим, чтобы выравнивающий фильтр вырабатывал набор подавляющих отражений. Поскольку нас интересуют выборки выровненного сигнала только в определенные моменты времени, проектирование подобного выравнивающего фильтра может быть довольно простой задачей.
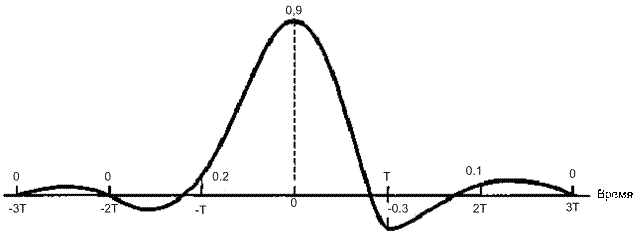
Рис. 3.25. Принятый искаженный импульс
Трансверсальный фильтр, изображенный на рис. 3.26, - это наиболее популярная форма легко настраиваемого выравнивающего фильтра, состоящего из канала задержки с отводами задержки на Т секунд (где Т - длительность символа). В подобном эквалайзере текущее и предыдущее значения принятого сигнала линейно взвешиваются коэффициентами эквалайзера или весовыми коэффициентами отводов ![]() , а затем суммируются для формирования выхода. Основной вклад вносит центральный отвод; вклады остальных отводов связаны с отражениями основного сигнала в течение последующих (и предыдущих) интервалов Т. Если бы можно было создать фильтр с бесконечным числом отводов, можно было бы так подобрать весовые коэффициенты, чтобы импульсный отклик системы равнялся всегда нулю, за исключением моментов взятия выборок; таким образом
, а затем суммируются для формирования выхода. Основной вклад вносит центральный отвод; вклады остальных отводов связаны с отражениями основного сигнала в течение последующих (и предыдущих) интервалов Т. Если бы можно было создать фильтр с бесконечным числом отводов, можно было бы так подобрать весовые коэффициенты, чтобы импульсный отклик системы равнялся всегда нулю, за исключением моментов взятия выборок; таким образом ![]() была бы точно равна обратной передаточной функции канала в формуле (3.85). Несмотря на то что фильтр с бесконечным числом отводов не относится к числу реализуемых, все же можно создать фильтр, достаточно хорошо аппроксимирующий идеальный случай.
была бы точно равна обратной передаточной функции канала в формуле (3.85). Несмотря на то что фильтр с бесконечным числом отводов не относится к числу реализуемых, все же можно создать фильтр, достаточно хорошо аппроксимирующий идеальный случай.
На рис. 3.26 выходы взвешенных отводов усиливаются, суммируются и подаются на устройство принятия решения. Весовые коэффициенты отводов ![]() должны выбираться так, чтобы вычитать эффекты интерференции из символов, соседствующих во времени с искомым символом. Предположим, что существует
должны выбираться так, чтобы вычитать эффекты интерференции из символов, соседствующих во времени с искомым символом. Предположим, что существует ![]() отводов с весовыми коэффициентами
отводов с весовыми коэффициентами ![]() . Выборки на выходе эквалайзера
. Выборки на выходе эквалайзера ![]() находятся путем следующей свертки выборок на входе
находятся путем следующей свертки выборок на входе ![]() и весовых коэффициентов
и весовых коэффициентов ![]() .
.
![]()
![]()
![]() (3.86)
(3.86)
где ![]() - временные коэффициенты, показанные в круглых скобках. (Время может быть как положительным, так и отрицательным.)
- временные коэффициенты, показанные в круглых скобках. (Время может быть как положительным, так и отрицательным.)
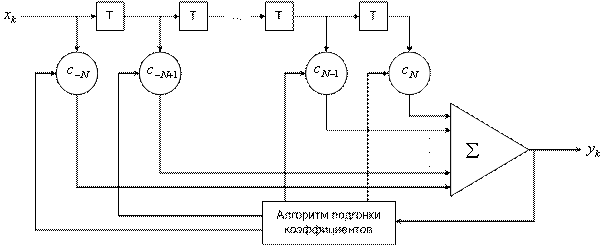
Рис.3.26. Трансверсальный фильтр
Коэффициент ![]() используется для обозначения смещения во времени и как идентификатор коэффициентов фильтра (адрес фильтра). В последнем случае
используется для обозначения смещения во времени и как идентификатор коэффициентов фильтра (адрес фильтра). В последнем случае ![]() показан как индекс. Если ввести векторы z и с и матрицу х
показан как индекс. Если ввести векторы z и с и матрицу х
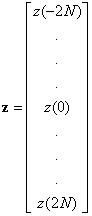
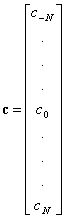 (3.87)
(3.87)
и
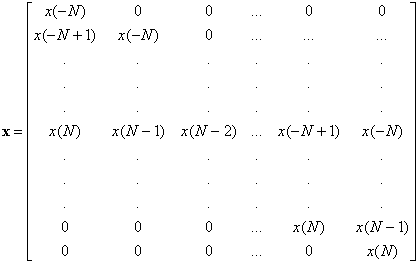 (3.88)
(3.88)
то соотношение между ![]() ,
, ![]() и
и ![]() можно записать в более компактной форме.
можно записать в более компактной форме.
![]() (3.89,а)
(3.89,а)
Если матрица х является квадратной, а число строк и столбцов соответствует числу элементов вектора с, то с можно выразить в следующем виде.
![]() (3.89,б)
(3.89,б)
Отметим, что в общем случае размер вектора z и число строк матрицы х могут быть любыми, поскольку нас может интересовать межсимвольная интерференция в точках взятия выборок, достаточно удаленных от основного лепестка рассматриваемого импульса. В формулах (3.86)-(3.88) индекс k выбирался так, чтобы число точек взятия выборок равнялось ![]() . Векторы z и с имеют размерность
. Векторы z и с имеют размерность ![]() и
и ![]() , соответственно, а матрица х не является квадратной и имеет размер
, соответственно, а матрица х не является квадратной и имеет размер ![]() на
на ![]() . В этом случае система уравнений (3.89,а) называется переопределенной (т.е. число уравнений превышает число неизвестных). Решать подобные уравнения можно с помощью детерминистского способа - метода обращения в нуль незначащих коэффициентов или статистического - метода решения с минимальной среднеквадратической ошибкой (mean-square error - MSE).
. В этом случае система уравнений (3.89,а) называется переопределенной (т.е. число уравнений превышает число неизвестных). Решать подобные уравнения можно с помощью детерминистского способа - метода обращения в нуль незначащих коэффициентов или статистического - метода решения с минимальной среднеквадратической ошибкой (mean-square error - MSE).
Обращение в нуль незначащих коэффициентов
Это решение начинается с отделения N верхних и N нижних строк матрицы х в уравнении (3.88). Таким образом, матрица х становится квадратной размером ![]() на
на ![]() , вектор z также имеет теперь размер
, вектор z также имеет теперь размер ![]() , а формула (3.89,а) определяет детерминированную систему
, а формула (3.89,а) определяет детерминированную систему ![]() уравнений. Предлагаемое решение минимизирует максимальное искажение, вызванное межсимвольной интерференцией, путем выбора весовых коэффициентов
уравнений. Предлагаемое решение минимизирует максимальное искажение, вызванное межсимвольной интерференцией, путем выбора весовых коэффициентов ![]() таким образом, чтобы сигнал на выходе эквалайзера был равен нулю в N точках взятия выборок по обе стороны от искомого импульса. Другими словами, весовые коэффициенты выбираются так, чтобы
таким образом, чтобы сигнал на выходе эквалайзера был равен нулю в N точках взятия выборок по обе стороны от искомого импульса. Другими словами, весовые коэффициенты выбираются так, чтобы
![]()
![]()
![]() (3.90)
(3.90)
Для нахождения ![]() весовых коэффициентов
весовых коэффициентов ![]() из системы
из системы ![]() уравнений используется выражение (3.90). Требуемая длина фильтра (число отводов) зависит от того, насколько сильно канал может «размазать» импульс. Для эквалайзера конечного размера максимальное искажение гарантированно будет минимизировано только в том случае, если глазковая диаграмма изначально имеет вид открытого глаза. В то же время при высокоскоростной передаче и в каналах, вводящих значительную межсимвольную интерференцию, до выравнивания глаз всегда закрыт [8]. Кроме того, эквалайзер, использующий метод обращения в нуль незначащих коэффициентов, не учитывает воздействие шума, поэтому такое решение не всегда является оптимальным.
уравнений используется выражение (3.90). Требуемая длина фильтра (число отводов) зависит от того, насколько сильно канал может «размазать» импульс. Для эквалайзера конечного размера максимальное искажение гарантированно будет минимизировано только в том случае, если глазковая диаграмма изначально имеет вид открытого глаза. В то же время при высокоскоростной передаче и в каналах, вводящих значительную межсимвольную интерференцию, до выравнивания глаз всегда закрыт [8]. Кроме того, эквалайзер, использующий метод обращения в нуль незначащих коэффициентов, не учитывает воздействие шума, поэтому такое решение не всегда является оптимальным.
Пример 3.5. Трехотводный эквалайзер, использующий метод обращения в нуль незначащих коэффициентов
Путем передачи единственного импульса или настроечного сигнала требуется определить весовые коэффициенты отводов выравнивающего трансверсального фильтра. Выравнивающий канал, изображенный на рис. 3.26, состоит всего из трех отводов. Пусть принят искаженный набор выборок импульса ![]() со значениями напряжения 0,0; 0,2; 0,9; -0,3; 0,1, как показано на рис. 3.25. Используйте метод обращения в нуль незначащих коэффициентов для нахождения коэффициентов
со значениями напряжения 0,0; 0,2; 0,9; -0,3; 0,1, как показано на рис. 3.25. Используйте метод обращения в нуль незначащих коэффициентов для нахождения коэффициентов ![]() , уменьшающих межсимвольную интерференцию так, чтобы выборки импульса после выравнивания имели значения
, уменьшающих межсимвольную интерференцию так, чтобы выборки импульса после выравнивания имели значения ![]() . Используя эти весовые коэффициенты, вычислите значения выборок выровненного импульса в моменты
. Используя эти весовые коэффициенты, вычислите значения выборок выровненного импульса в моменты ![]() . Чему равен вклад наибольшей амплитуды в межсимвольную интерференцию и чему равна сумма амплитуд всех вкладов?
. Чему равен вклад наибольшей амплитуды в межсимвольную интерференцию и чему равна сумма амплитуд всех вкладов?
Решение
При заданном импульсном отклике канала из формулы (3.89) получим следующее.
![]()
или
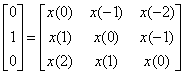
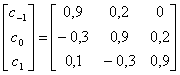
![]()
Решая систему трех уравнений, получаем следующие значения весовых коэффициентов.
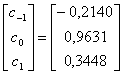
Значения выравненных выборок импульса ![]() , соответствующих временам взятия выборок
, соответствующих временам взятия выборок ![]() вычисляются с помощью формулы (3.89,а).
вычисляются с помощью формулы (3.89,а).
0,0000; -0,0428; 0,0000; 1,0000; 0,0000; -0,0071; 0,0345
Вклад наибольшей амплитуды в межсимвольную интерференцию равен 0,0428, а сумма амплитуд всех вкладов равна 0,0844. Очевидно, что эквалайзер с тремя отводами дает нулевое значение выровненного импульса в точках взятия выборки, соседствующих с основным лепестком. Если создать эквалайзер большего размера, он будет давать нулевое значение в большем числе точек взятия выборок.
Решение с минимальной среднеквадратической ошибкой
Более устойчивый эквалайзер можно получить, выбрав весовые коэффициенты ![]() , минимизирующие среднеквадратическую ошибку (mean-square error - MSE) всех членов, вносящих вклад в межсимвольную интерференцию, плюс мощности шума на выходе эквалайзера [9]. Среднеквадратическая ошибка определяется как математическое ожидание квадрата разности желаемого и обнаруженного информационных символов. Для получения решения с минимальной MSE можно использовать переопределенную систему уравнений (3.89,а), умножив обе ее части на
, минимизирующие среднеквадратическую ошибку (mean-square error - MSE) всех членов, вносящих вклад в межсимвольную интерференцию, плюс мощности шума на выходе эквалайзера [9]. Среднеквадратическая ошибка определяется как математическое ожидание квадрата разности желаемого и обнаруженного информационных символов. Для получения решения с минимальной MSE можно использовать переопределенную систему уравнений (3.89,а), умножив обе ее части на ![]() , что дает [10]
, что дает [10]
![]() (3.91,а)
(3.91,а)
и
![]() , (3.91,б)
, (3.91,б)
где ![]() является вектором взаимной корреляции, a
является вектором взаимной корреляции, a ![]() - автокорреляционной матрицей входного шумового сигнала. На практике
- автокорреляционной матрицей входного шумового сигнала. На практике ![]() и
и ![]() априори неизвестны, но могут быть вычислены приблизительно путем передачи через канал тестового сигнала и использования усреднения по времени для нахождения весовых коэффициентов из уравнения (3.91).
априори неизвестны, но могут быть вычислены приблизительно путем передачи через канал тестового сигнала и использования усреднения по времени для нахождения весовых коэффициентов из уравнения (3.91).
![]() (3.92)
(3.92)
При детерминистском решении метода обращения в нуль незначащих коэффициентов матрица х должна быть квадратной. Но для получения (статистического) решения с минимальной MSE начинать следует с переопределенной системы уравнений, а значит, неквадратной матрицы х, которая впоследствии преобразовывается в квадратную автокорреляционную матрицу ![]() , порождающую систему 2N+1 уравнений, решение которой дает значения весовых коэффициентов, минимизирующих MSE. Размер вектора с и число столбцов матрицы х соответствуют числу отводов выравнивающего фильтра. Большинство высокоскоростных модемов для выбора весовых коэффициентов используют критерий MSE, поскольку он лучше равновесного; он является более устойчивым при наличии шумов и большой межсимвольной интерференции [8].
, порождающую систему 2N+1 уравнений, решение которой дает значения весовых коэффициентов, минимизирующих MSE. Размер вектора с и число столбцов матрицы х соответствуют числу отводов выравнивающего фильтра. Большинство высокоскоростных модемов для выбора весовых коэффициентов используют критерий MSE, поскольку он лучше равновесного; он является более устойчивым при наличии шумов и большой межсимвольной интерференции [8].
Пример 3.6. Семиотводный эквалайзер с минимальной среднеквадратической ошибкой
Путем передачи единственного импульса или настроечного сигнала требуется определить весовые коэффициенты отводов выравнивающего трансверсального фильтра. Выравнивающий канал, изображенный на рис. 3.26, состоит из семи отводов. Пусть принят искаженный набор выборок импульса ![]() со значениями напряжения 0,0108; -0,0558; 0,1617; 1,0000; -0,1749; 0,0227; 0,0110. Используйте решение с минимальной среднеквадратической ошибкой для нахождения весовых коэффициентов
со значениями напряжения 0,0108; -0,0558; 0,1617; 1,0000; -0,1749; 0,0227; 0,0110. Используйте решение с минимальной среднеквадратической ошибкой для нахождения весовых коэффициентов ![]() , минимизирующих межсимвольную интерференцию. Используя эти весовые коэффициенты, вычислите значения выборок выровненного импульса в моменты
, минимизирующих межсимвольную интерференцию. Используя эти весовые коэффициенты, вычислите значения выборок выровненного импульса в моменты ![]() . Чему равен вклад наибольшей амплитуды в межсимвольную интерференцию и чему равна сумма амплитуд всех вкладов?
. Чему равен вклад наибольшей амплитуды в межсимвольную интерференцию и чему равна сумма амплитуд всех вкладов?
Решение
С помощью формулы (3.93) для семиотводного фильтра (N=3), можно записать матрицу х размером 4N+1 на 2N+1=13![]() 7.
7.

Используя матрицу х, можно получить автокорреляционную матрицу ![]() и вектор взаимной корреляции
и вектор взаимной корреляции ![]() , определенные формулами (3.91). С помощью компьютера матрица
, определенные формулами (3.91). С помощью компьютера матрица ![]() обращается, выполняется умножение матриц (см. формулу (3.92)), в результате чего получаются следующие весовые коэффициенты
обращается, выполняется умножение матриц (см. формулу (3.92)), в результате чего получаются следующие весовые коэффициенты ![]() .
.
-0,0116; 0,0108; 0,1659; 0,9495; -0,1318; 0,0670; -0,0269
Подставляя эти весовые коэффициенты в систему уравнений (3.89,а), находим 13 выравненных выборок ![]() в моменты времени
в моменты времени ![]() .
.
-0,0001; -0,0001; 0,0041; 0,0007; 0,0000; 1,0000;
0,0003; -0,0007; 0,0015; -0,0095; 0,0022; -0,0003
Вклад наибольшей амплитуды в межсимвольную интерференцию равен 0,0095, а сумма амплитуд всех вкладов равна 0,0195.
3.4.3.2. Эквалайзер с решающей обратной связью
Основное ограничение линейного эквалайзера, такого как трансверсальный фильтр, заключается в плохой производительности в каналах, имеющих спектральные нули [11]. Подобные каналы часто встречаются в приложениях мобильной радиосвязи. Эквалайзер с решающей обратной связью (decision feedback equalizer - DFE) - это нелинейное устройство, использующее предыдущее решение детектора для устранения межсимвольной интерференции из импульсов, демодулируемых в настоящий момент. Поскольку причиной интерференции являются хвосты предыдущих импульсов, по сути, из текущего импульса вычитается искажение, вызванное предыдущими импульсами.
На рис. 3.27 в виде блочной диаграммы изображен эквалайзер DFE, причем направляющий фильтр и фильтр обратной связи могут быть линейными; например, это может быть трансверсальный фильтр. На рисунке также показано адаптивное обновление весовых коэффициентов фильтра (см. следующий раздел). Нелинейность DFE вытекает из нелинейной характеристики детектора, обеспечивающего подачу сигнала на вход фильтра обратной связи. В основе работы DFE лежит следующее: если значения ранее обнаруженных символов известны (предыдущее решение предполагается точным), то межсимвольную интерференцию, внесенную символами, можно точно уравновесить на выходе направляющего фильтра путем вычитания значений предыдущих символов с соответствующими весовыми коэффициентами. Для удовлетворения выбранного критерия (например, минимальности среднеквадратической ошибки) весовые коэффициенты направляющего отвода и отвода обратной связи могут подгоняться одновременно.
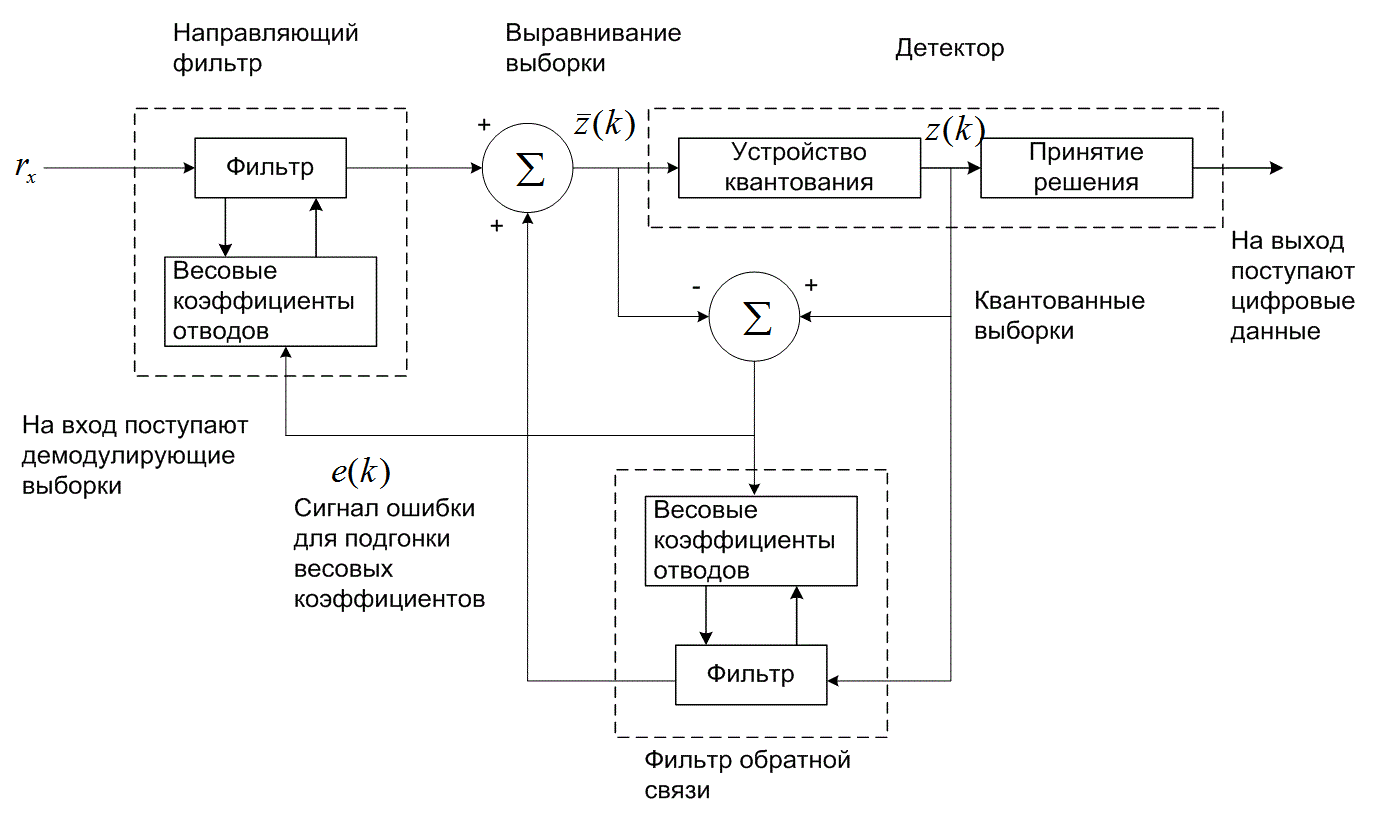
Рис.3.27. Эквалайзер с решающей обратной связью
При использовании единственного направляющего фильтра выход содержит шум канала, внесенный каждой выборкой, произведенной в фильтре. Преимуществом реализации DFE является то, что фильтр обратной связи не только используется для удаления межсимвольной интерференции, но и работает на бесшумных уровнях квантования, а значит на его выходе отсутствует шум канала.
3.4.4. Заданное и адаптивное выравнивание
В инвариантных относительно времени каналах с известными частотными характеристиками, характеристики канала могут измеряться, и, соответственно, могут подгоняться значения весовых коэффициентов отводов. Если весовые коэффициенты остаются фиксированными в течение всего процесса передачи данных, выравнивание называется заданным (preset); простой метод заданного выравнивания заключается в установке весовых коэффициентов ![]() , согласно некоторым усредненным знаниям о канале. Такой метод использовался для передачи информации по телефонным каналам со скоростью, не превышающей 2400 бит/с. Еще один метод заданного выравнивания состоит в передаче настроечной последовательности, которая в приемнике сравнивалась с последовательностью, сгенерированной локально. Отличия последовательностей позволяют установить весовые коэффициенты
, согласно некоторым усредненным знаниям о канале. Такой метод использовался для передачи информации по телефонным каналам со скоростью, не превышающей 2400 бит/с. Еще один метод заданного выравнивания состоит в передаче настроечной последовательности, которая в приемнике сравнивалась с последовательностью, сгенерированной локально. Отличия последовательностей позволяют установить весовые коэффициенты ![]() . Важным моментом использования любой разновидности заданного выравнивания является то, что установка параметров производится либо единожды, либо в исключительно редких случаях (например, при прерывании передачи и необходимости ее повторной настройки).
. Важным моментом использования любой разновидности заданного выравнивания является то, что установка параметров производится либо единожды, либо в исключительно редких случаях (например, при прерывании передачи и необходимости ее повторной настройки).
Тип выравнивания, способный отслеживать постепенные изменения, называется адаптивным (adaptive). Его реализация может включать периодическую или непрерывную «подборку» весовых коэффициентов отводов. Периодическая корректировка выполняется путем периодической передачи начальной комбинации битов или краткой настроечной последовательности, заранее известной приемнику. Кроме того, начальная комбинация битов используется приемником для определения начала передачи, установки уровня автоматической регулировки усиления (automatic gain control - AGC) и для согласования с принятым сигналом внутренних часов и местных гетеродинов. Непрерывная подстройка осуществляется посредством замещения известной тестовой последовательности набором информационных символов, которые получены на выходе эквалайзера и считаются известными данными. При непрерывной и автоматической (наиболее распространенный подход) настройке используется метод, управляемый решением (decision directed) [11]. Название метода не стоит путать с DFE - эквалайзером с решающей обратной связью. Управление решением связано только со способом юстировки (с помощью сигнала от детектора) весовых коэффициентов отводов фильтра. Эквалайзер DFE - это наличие дополнительного фильтра на выходе детектора, рекурсивным образом возвращающего сигнал на вход детектора. Следовательно, при использовании DFE существует два фильтра (направляющий и фильтр обратной связи), обрабатывающие данные для снижения межсимвольной интерференции.
Недостатком заданного выравнивания является то, что оно требует предварительной настройки в начале каждой новой передачи. Кроме того, нестационарные каналы, вследствие межсимвольной интерференции и фиксированных весовых коэффициентах отводов, могут приводить к ухудшению производительности системы. Адаптивное выравнивание, в частности адаптивное выравнивание, управляемое решением, успешно устраняет межсимвольную интерференцию, если первоначальная вероятность ошибки не превышает один процент (эмпирическое правило). Если вероятность ошибки превышает один процент, эквалайзер, управляемый решением, может и не дать требуемого результата. Общее решение этой проблемы - инициализировать эквалайзер с альтернативным процессом, (таким, как передача начальной комбинации битов), что позволит обеспечить низкую вероятность ошибки в канале, а затем переключиться в режим управления решением. Чтобы избежать служебных издержек, вносимых начальной комбинацией битов, проекты многих систем предусматривают работу в режиме непрерывного широковещания с использованием для первоначальной оценки канала алгоритмов слепого выравнивания (blind equalization). Эти алгоритмы согласовывают коэффициенты фильтра со статистикой выборок, а не с решениями относительно значений выборок [11].
Для оценки оптимальных коэффициентов автоматические эквалайзеры используют итеративные методы. Система уравнений, приведенная в выражении (3.93), не учитывает воздействие шума канала. При получении устойчивого решения для значений весовых коэффициентов фильтра, требуется усреднять либо данные для устойчивой статистики сигнала, либо зашумленное решение, полученное из зашумленных данных. Сложность алгоритма и проблемы численной устойчивости часто приводит к разработке алгоритмов, усредняющих зашумленные решения. Наиболее надежным из этого класса алгоритмов является алгоритм минимальной среднеквадратической (least-mean-square - LMS) ошибки. Каждая итерация этого алгоритма использует зашумленную оценку градиента ошибок для регулировки весовых коэффициентов относительно снижения среднеквадратической ошибки. Градиент шума - это просто произведение ![]() скалярного значения ошибки
скалярного значения ошибки ![]() и вектора данных
и вектора данных ![]() . Вектор
. Вектор ![]() - это вектор выборок канала, которые подверглись воздействию шума и в момент k находились на выравнивающем фильтре. Выше использовалось следующее математическое представление: передавался импульс, и выравнивающий фильтр работал с последовательностью выборок (вектором), представляющей импульсный отклик канала. Эти принятые выборки (в виде сдвига во времени) изображались как матрица х. Теперь, вместо использования отклика на импульс, предполагается передача данных на вход фильтра (рис. 3.27), соответственно определяется вектор принятых выборок
- это вектор выборок канала, которые подверглись воздействию шума и в момент k находились на выравнивающем фильтре. Выше использовалось следующее математическое представление: передавался импульс, и выравнивающий фильтр работал с последовательностью выборок (вектором), представляющей импульсный отклик канала. Эти принятые выборки (в виде сдвига во времени) изображались как матрица х. Теперь, вместо использования отклика на импульс, предполагается передача данных на вход фильтра (рис. 3.27), соответственно определяется вектор принятых выборок ![]() , представляющий информационный отклик канала. Ошибка записывается как разность желаемого сигнала и сигнала, полученного на выходе фильтра.
, представляющий информационный отклик канала. Ошибка записывается как разность желаемого сигнала и сигнала, полученного на выходе фильтра.
![]() (3.93)
(3.93)
Здесь ![]() - желаемый выходной сигнал (выборка без межсимвольной интерференции), а
- желаемый выходной сигнал (выборка без межсимвольной интерференции), а ![]() - оценка
- оценка ![]() в момент времени k (производится в устройстве квантования, показанном на рис. 3.27), имеющая следующий вид.
в момент времени k (производится в устройстве квантования, показанном на рис. 3.27), имеющая следующий вид.
![]() (3.94)
(3.94)
В формуле (3.94) суммирование представляет свертку входящих информационных выборок с весовыми коэффициентами отводов ![]() , где
, где ![]() - коэффициент
- коэффициент ![]() -го отвода в момент времени k, а
-го отвода в момент времени k, а ![]() - транспонированный вектор весовых коэффициентов в момент времени k. Далее будет показано, что итеративный процесс, обновляющий значения весовых коэффициентов в каждый момент времени k, имеет следующий вид.
- транспонированный вектор весовых коэффициентов в момент времени k. Далее будет показано, что итеративный процесс, обновляющий значения весовых коэффициентов в каждый момент времени k, имеет следующий вид.
![]() (3.95)
(3.95)
Здесь ![]() - вектор весовых коэффициентов фильтра в момент времени k, а
- вектор весовых коэффициентов фильтра в момент времени k, а ![]() - малый член, ограничивающий шаг коэффициентов, а значит, контролирующий скорость сходимости алгоритма и дисперсию устойчивого решения. Это простое соотношение является следствием принципа ортогональности, утверждающего, что ошибка, сопровождающая оптимальное решение, ортогональна обрабатываемым данным. Поскольку алгоритм рекурсивен (по отношению к весовым коэффициентам), необходимо следить за его устойчивостью. Устойчивость гарантируется, если параметр
- малый член, ограничивающий шаг коэффициентов, а значит, контролирующий скорость сходимости алгоритма и дисперсию устойчивого решения. Это простое соотношение является следствием принципа ортогональности, утверждающего, что ошибка, сопровождающая оптимальное решение, ортогональна обрабатываемым данным. Поскольку алгоритм рекурсивен (по отношению к весовым коэффициентам), необходимо следить за его устойчивостью. Устойчивость гарантируется, если параметр ![]() меньше значения обратной энергии данных в фильтре. Если алгоритм является устойчивым, он в среднем сходится к оптимальному решению, при этом его дисперсия пропорциональна параметру
меньше значения обратной энергии данных в фильтре. Если алгоритм является устойчивым, он в среднем сходится к оптимальному решению, при этом его дисперсия пропорциональна параметру ![]() . Таким образом, желательно, чтобы параметр сходимости
. Таким образом, желательно, чтобы параметр сходимости ![]() был больше (для более быстрой сходимости), но не настолько, чтобы привести к неустойчивости, хотя, с другой стороны, малый параметр
был больше (для более быстрой сходимости), но не настолько, чтобы привести к неустойчивости, хотя, с другой стороны, малый параметр ![]() обеспечивает малую дисперсию. Обычно для получения низкодисперсного устойчивого решения
обеспечивает малую дисперсию. Обычно для получения низкодисперсного устойчивого решения ![]() выбирается равным фиксированной небольшой величине [12]. Существуют схемы [13], позволяющие
выбирается равным фиксированной небольшой величине [12]. Существуют схемы [13], позволяющие ![]() меняться от больших значений к меньшим в процессе получения устойчивого решения.
меняться от больших значений к меньшим в процессе получения устойчивого решения.
Отметим, что уравнения (3.93)-(3.95) приведены в контексте вещественных сигналов. Если используется квадратурная реализация, так что сигнал описывается вещественной и мнимой (или синфазной и квадратурной) упорядоченными парами, то каждый канал на рис. 3.27 в действительности состоит из двух каналов, и уравнения (3.93)-(3.95) необходимо записывать в комплексной форме.
3.4.5. Частота обновления фильтра
Выравнивающие фильтры классифицируются по частоте дискретизации входящего сигнала. Трансверсальный фильтр с отводами, размещенными через Т секунд, где Т - длительность передачи символа, называется эквалайзером с символьным разделением (symbol-spaced equalizer). Процесс дискретизации выхода эквалайзера с частотой ![]() приводит к наложению, если полоса сигнала не ограничена строго величиной
приводит к наложению, если полоса сигнала не ограничена строго величиной ![]() Гц, т.е. спектральные компоненты сигнала, не разделенные промежутком
Гц, т.е. спектральные компоненты сигнала, не разделенные промежутком ![]() Гц, накладываются. Наложенная версия сигнала может давать спектральные нули [8]. Частота обновления фильтра, превышающая скорость передачи символов, помогает смягчить эту проблему. Эквалайзеры, использующие подобный метод, называются эквалайзерами с фракционным разделением (fractionally-spaced equalizer). В таких устройствах отводы фильтра разделены промежутками
Гц, накладываются. Наложенная версия сигнала может давать спектральные нули [8]. Частота обновления фильтра, превышающая скорость передачи символов, помогает смягчить эту проблему. Эквалайзеры, использующие подобный метод, называются эквалайзерами с фракционным разделением (fractionally-spaced equalizer). В таких устройствах отводы фильтра разделены промежутками
![]() секунд, (3.96)
секунд, (3.96)
где через ![]() обозначен избыток полосы. Другими словами, ширина принятого сигнала равна следующему.
обозначен избыток полосы. Другими словами, ширина принятого сигнала равна следующему.
![]() (3.97)
(3.97)
![]() необходимо выбрать так, чтобы передаточная функция эквалайзера
необходимо выбрать так, чтобы передаточная функция эквалайзера ![]() была значительно шире и охватывала весь спектр сигнала. Отметим, что сигнал на выходе эквалайзера по-прежнему выбирается с частотой
была значительно шире и охватывала весь спектр сигнала. Отметим, что сигнал на выходе эквалайзера по-прежнему выбирается с частотой ![]() , но поскольку весовые коэффициенты отводов разделены промежутками
, но поскольку весовые коэффициенты отводов разделены промежутками ![]() (входящий сигнал эквалайзера выбирается с частотой
(входящий сигнал эквалайзера выбирается с частотой ![]() ), выравнивание принятого сигнала происходит до наложения его частотных компонентов. Моделирование эквалайзеров в телефонных линиях с
), выравнивание принятого сигнала происходит до наложения его частотных компонентов. Моделирование эквалайзеров в телефонных линиях с ![]() показывает, что эквалайзеры с фракционным разделением превосходят эквалайзеры с символьным разделением [14].
показывает, что эквалайзеры с фракционным разделением превосходят эквалайзеры с символьным разделением [14].
Литература
1. Nyquist H. Thermal Agitation of Electric Charge in Conductors. Phys. Rev., vol. 32, July 1928, pp. 110-113.
2. Van Trees H. L. Detection, Estimation and Modulation Theory. Part 1, John Wiley & Sons, Inc., New York, 1968.
3. Arthurs E. and Dym H. On the Optimum Detection of Digital Signals in the Presence of White, Gaussian Noise - A Geometric Interpretation of Three Basic Data Transmission Systems. IRE Trans. Commun. Syst, December, 1962.
4. Wozencraft J. M. and Jacobs I. M. Principles of Communication Engineering. John Wiley & Sons, Inc., New York, 1965.
5. Borjesson P. O. and Sundberg C. E. Simple Approximations of the Error Function Q(x) for Communications Applications. IEEE Trans. Commun., vol. COM27, March, 1979, pp. 639-642.
6. Nyquist H. Certain Topics of Telegraph Transmission Theory. Trans. Am. Inst. Electr. Eng., vol. 47, April, 1928, pp. 617-644.
7. Hanzo L. and Stefanov J. The AN-European Digital Cellular Mobile Radio System - Known as GSM. Mobile Radio Communications, edited by R. Steele, Chapter 8, Pentech Press, London, 1992.
8. Qureshi S. U. H. Adaptive Equalization. Proc. IEEE, vol. 73, n. 9, September, 1985, pp.1340-1387.
9. Lucky R. W., Salz J. and Weldon E. J., Jr. Principles of Data Communications. Mc-Graw Hill Book Co., New York, 1968.
10. Harris F. and Adams B. Digital Signal Processing to Equalize the Pulse response of Non Synchronous Systems Such as Encountered in Sonar and Radar. Proc. of the Twenty-Fourth Annual ASILOMAR Conference on Signals, Systems, and Computers, Pacific Grove, California, November, 5-7, 1990.
11. Proakis J. G. Digital Communications. McGraw-Hill Book Company, New York, 1983.
12. Feuer A. and Weinstein E. Convergence Analysis of LMS Filters with Uncorrelated Gaussian Data. IEEE Trans, on ASSP, vol. V-33, pp. 220-230, 1985.
13. Macchi O. Adaptive Processing: Least Mean Square Approach With Applications in Transmission. John Wiley & Sons, New York, 1995.
14. Benedetto S., Biglieri E. and Castellani V. Digital Transmission Theory. Prentice Hall, 1987.
Задачи
3.1. Определите, являются ли сигналы ![]() и
и ![]() ортогональными на интервале
ортогональными на интервале ![]() , где
, где ![]() ,
, ![]() ,
, ![]() , в следующих случаях.
, в следующих случаях.
а) ![]() и
и ![]()
б) ![]() и
и ![]()
в) ![]() и
и ![]()
г) ![]() и
и ![]()
д) ![]() и
и ![]()
е) ![]() и
и ![]()
3.2. а) Покажите, что три функции, приведенные на рис. 33.1, попарно ортогональны на интервале (-2, 2).
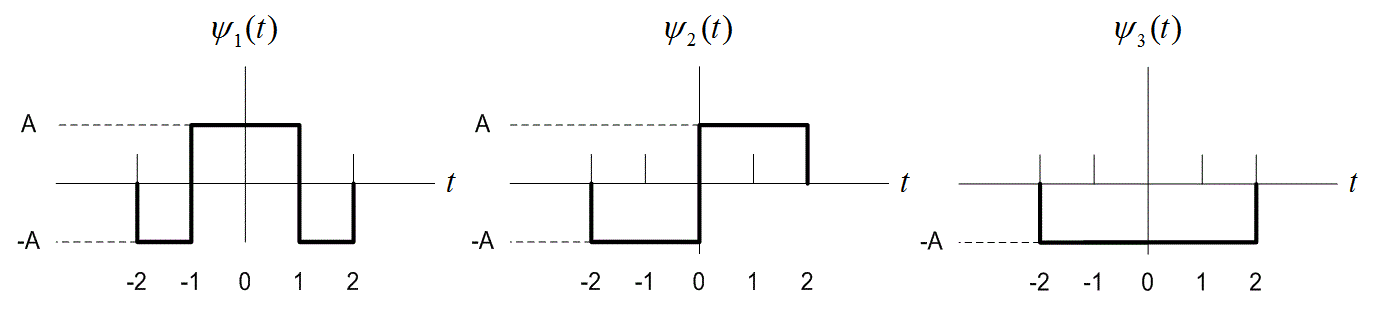
Рис. З3.1
б) Определите значение константы А, преобразующей набор функций из п. а в набор ортонормированных функций.
в) Выразите сигнал ![]() через ортонормированные функции, полученные при выполнении п. б.
через ортонормированные функции, полученные при выполнении п. б.
![]()
![]()
![]()
![]()
3.3. Даны следующие функции
![]() и
и ![]()
Определите константу А, при которой функции ![]() и
и ![]() ортогональны на интервале
ортогональны на интервале ![]() .
.
3.4. Предположим, что используется некоторая система цифровой связи; сигнальные компоненты вне приемника-коррелятора с равной вероятностью принимают значения ![]() или -1 В. Определите вероятность появления ошибочного бита, если гауссов шум на вы ходе коррелятора имеет единичную дисперсию.
или -1 В. Определите вероятность появления ошибочного бита, если гауссов шум на вы ходе коррелятора имеет единичную дисперсию.
3.5. Биполярный двоичный сигнал ![]() - это импульс +1 или -1 В на интервале
- это импульс +1 или -1 В на интервале ![]() . К сигналу добавляется аддитивный белый гауссов шум с двусторонней спектральной плотностью мощности
. К сигналу добавляется аддитивный белый гауссов шум с двусторонней спектральной плотностью мощности ![]() Вт/Гц. Если обнаружение принятого сигнала производится с помощью согласованного фильтра, определите максимальную скорость передачи битов, которую можно поддерживать при вероятности появления ошибочного бита
Вт/Гц. Если обнаружение принятого сигнала производится с помощью согласованного фильтра, определите максимальную скорость передачи битов, которую можно поддерживать при вероятности появления ошибочного бита ![]() .
.
3.6. Биполярные импульсные сигналы ![]()
![]() амплитуды ±1 В принимаются при шуме AWGN с дисперсией 0,1
амплитуды ±1 В принимаются при шуме AWGN с дисперсией 0,1 ![]() . Определите оптимальный (дающий минимальную вероятность ошибки) порог
. Определите оптимальный (дающий минимальную вероятность ошибки) порог ![]() для обнаружения с использованием согласованного фильтра при следующих априорных вероятностях: (a)
для обнаружения с использованием согласованного фильтра при следующих априорных вероятностях: (a) ![]() ; (б)
; (б) ![]() ; (в)
; (в) ![]() . Объясните влияние априорных вероятностей на значение
. Объясните влияние априорных вероятностей на значение ![]() . (Подсказка: используйте формулы (Б. 10)-(Б. 12).)
. (Подсказка: используйте формулы (Б. 10)-(Б. 12).)
3.7. Двоичная система связи передает сигналы ![]()
![]() . Тестовая статистика приемника
. Тестовая статистика приемника ![]() , где компонент сигнала
, где компонент сигнала ![]() равен
равен ![]() или
или ![]() , а компонент шума
, а компонент шума ![]() имеет равномерное распределение. Плотности условного распределения
имеет равномерное распределение. Плотности условного распределения ![]() даются выражениями
даются выражениями
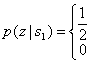
![]()
![]()
![]()
и
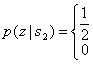
![]()
![]()
![]()
Определите вероятность появления ошибки ![]() для равновероятной передачи сигналов и использования оптимального порога принятия решения.
для равновероятной передачи сигналов и использования оптимального порога принятия решения.
3.8. а) Чему равна минимальная ширина полосы, необходимая для передачи без межсимвольной интерференции сигнала с использованием 16-уровневой кодировки РАМ на скорости 10 Мбит/с?
б) Чему равен коэффициент сглаживания, если доступная полоса равна 1,375 МГц?
3.9. Сигнал речевого диапазона (300-3300 Гц) оцифровывается так, что квантовое искажение ![]() удвоенного максимального напряжения сигнала. Предположим, что частота дискретизации равна 8000 выборок/с и используется 32-уровневая кодировка РАМ. Определите теоретическую минимальную ширину полосы, при которой еще не возникает межсимвольная интерференция.
удвоенного максимального напряжения сигнала. Предположим, что частота дискретизации равна 8000 выборок/с и используется 32-уровневая кодировка РАМ. Определите теоретическую минимальную ширину полосы, при которой еще не возникает межсимвольная интерференция.
3.10. Двоичные данные передаются со скоростью 9600 бит/с с использованием 8-уровневой модуляции РАМ и фильтра с характеристикой типа приподнятого косинуса. Частотный отклик системы не превышает 2,4 кГц.
а) Чему равна скорость передачи символов?
б) Чему равен коэффициент сглаживания характеристики фильтра?
3.11. Сигнал речевого диапазона (300-3300 Гц) дискретизируется с частотой 8000 выборок/с. Выборки можно передавать сразу в виде импульсов РАМ или каждую выборку вначале можно преобразовать в формат РСМ и использовать для передачи двоичные (РСМ) сигналы.
а) Чему равна минимальная ширина полосы системы, необходимая для обнаружения импульсов РАМ без межсимвольной интерференции и с параметром сглаживания фильтра ![]() ?
?
б) Используя ту же характеристику выравнивания, что и в предыдущем пункте, определите минимальную ширину полосы, необходимую для обнаружения двоичных сигналов (кодировка РСМ), если выборки квантовались с использованием восьми уровней.
в) Повторите п. б для 128 уровней.
3.12. Аналоговый сигнал форматирован в формате РСМ и передается с использованием двоичных сигналов через канал с полосой 100 кГц. Предполагается, что используются 32 уровня квантования и что полная эквивалентная передаточная функция - приподнятый косинус с выравниванием ![]() .
.
а) Найдите максимальную скорость передачи битов, которую может поддерживать система без межсимвольной интерференции.
б) Найдите максимальную ширину исходного аналогового сигнала, возможную при приведенных параметрах.
в) Повторите пп. а и б для 8-уровневой кодировки РАМ.
3.13. Равновероятные двоичные импульсы в кодировке RZ когерентно обнаруживаются в гауссовом канале с ![]() Вт/Гц. Предполагается, что синхронизация идеальна, амплитуда принятых импульсов равна 100 мВ и вероятность ошибки
Вт/Гц. Предполагается, что синхронизация идеальна, амплитуда принятых импульсов равна 100 мВ и вероятность ошибки ![]() ; найдите наибольшую скорость передачи данных, возможную в описанной системе.
; найдите наибольшую скорость передачи данных, возможную в описанной системе.
3.14. Двоичные импульсы в кодировке NRZ передаются по кабелю, ослабляющему сигнал на 3 дБ (на пути от передатчика к приемнику). Эти импульсы когерентно обнаруживаются приемником, а скорость передачи данных равна 56 Кбит/с. Шум считать гауссовым с ![]() Вт/Гц. Чему равна минимальная мощность, необходимая для передачи с вероятностью ошибки
Вт/Гц. Чему равна минимальная мощность, необходимая для передачи с вероятностью ошибки ![]() ?
?
3.15. Покажите, что минимальная ширина полосы по Найквисту для случайной двоичной последовательности с биполярными импульсами идеальной формы равна ширине полосы шумового эквивалента. Подсказка: спектральная плотность мощности случайной последовательности биполярных импульсов определяется формулой (1.38), а ширина полосы шумового эквивалента дана в разделе 1.7.2.
3.16. Дана четырехуровневая последовательность символов сообщений в кодировке РАМ: {+1,+1,-1,+3,+1,+3}, где элементами алфавита являются числа {±1,±3}. Импульсы формируются фильтром с характеристикой типа корня из приподнятого косинуса; время поддержки каждого фильтрованного импульса составляет 6 периодов передачи символа, передаваемая последовательность - аналоговый сигнал, показанный на рис. 3.23, а. Отметим, что сигналы «размываются» вследствие межсимвольной интерференции, вносимой фильтром. Покажите, как можно реализовать набор N корреляторов для выполнения демодуляции принятой последовательности импульсов ![]() на согласованном фильтре, если число символов, переданных в течение длительности импульса, также равно N. (Подсказка: для набора корреляторов используйте опорные сигналы вида
на согласованном фильтре, если число символов, переданных в течение длительности импульса, также равно N. (Подсказка: для набора корреляторов используйте опорные сигналы вида ![]() , где k = 0,...,5, а Т - время передачи символа.)
, где k = 0,...,5, а Т - время передачи символа.)
3.17. Желательным импульсным откликом системы является идеальный отклик ![]() , где
, где ![]() - импульсная функция. Предполагается, что канал так вводит межсимвольную интерференцию, что общий импульсный отклик становится равным
- импульсная функция. Предполагается, что канал так вводит межсимвольную интерференцию, что общий импульсный отклик становится равным ![]() , где
, где ![]() , а Т - длительность передачи символа. Выведите выражения для импульсного отклика фильтра, который реализует метод обращения в нуль незначащих коэффициентов и уменьшает последствия межсимвольной интерференции. Покажите, что этот фильтр подавляет межсимвольную интерференцию. Если полученное подавление окажется недостаточным, как можно будет модифицировать фильтр для более сильного подавления межсимвольной интерференции?
, а Т - длительность передачи символа. Выведите выражения для импульсного отклика фильтра, который реализует метод обращения в нуль незначащих коэффициентов и уменьшает последствия межсимвольной интерференции. Покажите, что этот фильтр подавляет межсимвольную интерференцию. Если полученное подавление окажется недостаточным, как можно будет модифицировать фильтр для более сильного подавления межсимвольной интерференции?
3.18. Результатом передачи одного импульса является принятая последовательность выборок (импульсный отклик) со значениями 0,1; 0,3; -0,2; 1,0; 0,4; -0,1; 0,1, где наиболее ранней является крайняя слева выборка. Значение 1,0 соответствует основному лепестку импульса, а другие - соседним выборкам. Спроектируйте трехотводный трансверсальный эквалайзер, подавляющий межсимвольную интерференцию в точках дискретизации по обе стороны основного лепестка. Вычислите значения выровненных импульсов в моменты времени k=0,±1,...,±3. Чему после выравнивания равен вклад наибольшей амплитуды в межсимвольную интерференцию и чему равна сумма амплитуд всех вкладов?
3.19. Повторите задачу 3.18, если импульсный отклик канала описывается следующими принятыми выборками: 0,01; 0,02; -0,03; 0,1; 1,0; 0,2: -0,1; 0,05; 0,02. С помощью компьютера найдите весовые коэффициенты девятиотводного трансверсального эквалайзера, удовлетворяющие критерию минимальности среднеквадратической ошибки. Вычислите значения импульсов на выходе эквалайзера в моменты времени k=0,±1,...,±8. Чему после выравнивания равен вклад наибольшей амплитуды в межсимвольную интерференцию и чему равна сумма амплитуд всех вкладов?
3.20. В данной главе отмечалось, что устройства обработки сигналов, такие как блоки перемножения и интегрирования, обычно работают с сигналами, имеющими размерность вольт. Таким образом, передаточная функция таких устройств должна выражаться в этих же единицах. Нарисуйте блочную диаграмму интегратора произведений, показывающую единицы сигналов в каждом проводнике и передаточную функцию устройства в каждом блоке. (Подсказка: см. раздел 3.2.5.1.)
Вопросы для самопроверки
3.1. При узкополосной передаче принятые сигналы уже имеют вид импульсов. Почему для восстановления импульсного сигнала требуется демодулятор (см. начало главы 3)?
3.2. Почему отношение ![]() , является естественным критерием качества систем цифровой связи (см. раздел 3.1.5)?
, является естественным критерием качества систем цифровой связи (см. раздел 3.1.5)?
3.3. При представлении упорядоченных во времени событий какая дилемма может легко привести к путанице между самым старшим битом и самым младшим (см. раздел 3.2.3.1)?
3.4. Термин согласованный фильтр часто используется как синоним термина коррелятор. Как такое возможно при совершенно разных математических операциях, описывающих их работу (см. раздел 3.2.3.1)?
3.5. Опишите два точных способа сравнения различных кривых, описывающих зависимость вероятности появления ошибочного бита от отношения ![]() (см. раздел 3.2.5.3).
(см. раздел 3.2.5.3).
3.6. Существуют ли функции фильтров формирования импульсов (отличные от приподнятого косинуса), дающие нулевую межсимвольную интерференцию (см. раздел 3.3)?
3.7. До какой степени можно сжать полосу, не подвергаясь при этом межсимвольной интерференции (см. раздел 3.3.1.1)?
3.8. Ухудшение качества сигнала определяется двумя основными факторами: снижением отношения сигнал/шум и искажением, приводящим к не поддающейся улучшению вероятности возникновения ошибки. Чем отличаются эти факторы (см. раздел 3.3.2)?
3.9. Иногда увеличение отношения ![]() не останавливает ухудшение качества, вызванное межсимвольной интерференцией. Когда это происходит (см. раздел 3.3.2)?
не останавливает ухудшение качества, вызванное межсимвольной интерференцией. Когда это происходит (см. раздел 3.3.2)?
3.10. Чем отличается эквалайзер, реализовывающий метод обращения в нуль незначащих коэффициентов, от эквалайзера, реализовывающего решение с минимальной среднеквадратической ошибкой (см. раздел 3.4.3.1)?

