1. Общие сведения о линиях связи и направляющих системах связи

1.1. Роль и место направляющих систем в системах связи. Виды линий связи и их основные свойства

1.2. Классификация, конструкции и частотные диапазоны направляющих систем

2. Построение сетей электросвязи

3. Кабели на основе направляющих систем

3.1. Электрические кабели

3.2. Оптические кабели

4. Электродинамика направляющих систем

4.1. Общие положения

4.2. Энергетические соотношения для электромагнитного поля

4.3. Режимы передачи по направляющим системам

4.4. Классы и типы волн в НСС

4.5. Электромагнитные процессы в проводниках и диэлектриках

4.6. Уравнение однородной линии

5. Теория направляющих систем

5.1. Передача энергии по симметричной цепи с учётом потерь

5.2. Внутренняя индуктивность, емкость и сопротивление изоляции симметричной цепи

5.3. Вторичные параметры передачи симметричных цепей

5.4. Коаксиальные цепи. Электрические процессы в коаксиальных цепях

5.5. Параметры передачи коаксиальных цепей

5.6. Оптимальное соотношение диаметров проводников коаксиальной цепи

5.7. Свойства неоднородных линий

6. Волноводы

6.1. Круглый волновод

7. Волоконные световоды

7.1. Полное внутренние отражения

7.2. Числовая апертура и апертурный угол

7.3. Основные положения волновой теории ВС

7.4. Дисперсия в световодах

7.5. Затухание в волоконных световодах

1. Общие сведения о линиях связи и направляющих системах связи

1.1. Роль и место направляющих систем  в системах связи. Виды линий связи и их основные свойства

Систему передачи, содержащую направляющую систему (НС), логично представить обобщенной схемой (рис. 1.1).

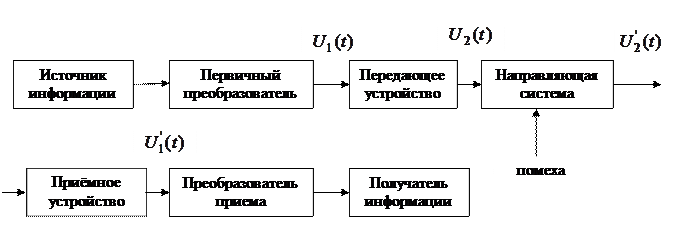
Рис. 1.1. Обобщенная схема системы передачи

На НС действуют помехи, в тракте системы передачи могут возникать различного рода искажения. Поэтому

                          (1.1)

Действующие  на НС помехи делятся на внешние и внутренние. Внешние помехи вызваны действием сторонних электромагнитных полей. Внутренние  помехи обусловлены действием электромагнитных полей соседних проводников в направляющей системе (или взаимными влияниями). Практически идеальной направляющей системой является волоконный световод, т. к. на него не действуют внешние поля и в световоде отсутствуют взаимные влияния.

Направляющая система  - это непрерывная по длине  конструкция, направляющая распространение электромагнитной энергии в заданном направлении, т. е., обладающая канализирующими свойствами. Такими свойствами обладает граница раздела сред с разными электрическими параметрами (рис 1.2 ).

Любая материальная среда характеризуется такими параметрами:

• удельным электрическим сопротивлением  p, 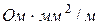 или удельной электрической проводимостью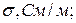
• абсолютной магнитной проницаемостью 
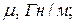
• абсолютной диэлектрической проницаемостью E, Ф/м;

Следует учесть, что ; ;  , где ,  – относительная диэлектрическая и магнитная проницаемости соответственно;  Ф/м – абсолютная диэлектрическая проницаемость вакуума;    Гн/м – абсолютная магнитная проницаемость вакуума, n – коэффициент преломления среды.

Рис. 1.2. Обобщённая направляющая система

К  направляющим системам предъявляются следующие требования:

• высокая информационная ёмкость;
• малые потери электромагнитной энергии в процессе её распространения;
• возможность передачи различных видов информации, т.е. сигналов с различными видами модуляции;
• малые взаимные влияния;
• постоянство параметров НС в процессе длительного срока эксплуатации;
• обеспечение необходимого качества и дальности связи.

         По направляющим системам передаются различные виды информации (табл. 1.1).

Таблица 1 .1

Виды информации	Полоса частот, кГц	Количество КТЧ
Телефония	4	1
Радиовещание	8 – 12	2 - 3
Телевидение	6000	1500
Телеграфия	4/(18…24)	1/(18…24)
Передача данных	4…240	1…60

Непременным, одним из наиболее сложных и дорогостоящих элементов техники связи являются линии связи (ЛС). Линия связи – комплекс технических сооружений, обеспечивающий передачу как узкополосных, так и широкополосных каналов, используемых для передачи информации от отправителя к получателю на заданное расстояние с заданным качеством. Эффективность работы систем определяется качеством ЛС, их свойствами, параметрами, воздействием на ЛС различных факторов. Линии связи состоят из нескольких подсистем, обеспечивающих их функционирование: оконечных пунктов, обслуживаемых и необслуживаемых усилительных (регенерационных) пунктов.

Классификация линий связи. Линии связи делятся на два типа – беспроводные (радиолинии) и проводные на основе тех или иных направляющих систем. Классификация ЛС приведена на рис 1.3.1

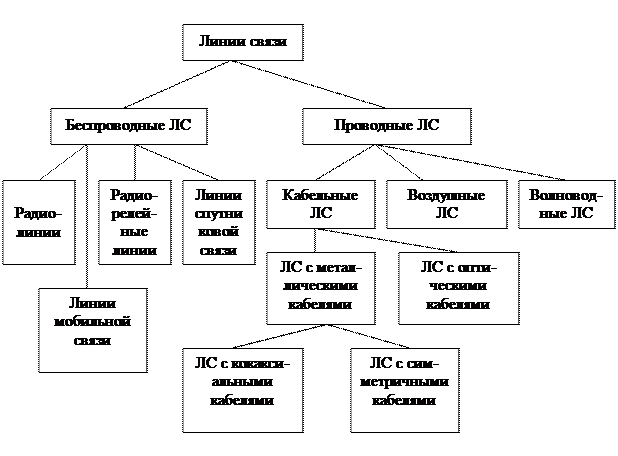
Рис. 1.3. Классификация линий связи

Отличительной особенностью проводных ЛС является  то, что передача информации от одного абонента к другому осуществляется по специально созданным на основе направляющих систем цепям. Характер распространения электромагнитных волн в различных средах и направляющих системах определяется частотными диапазонами, в которых работают эти системы.

Беспроводные и проводные ЛС имеют свои особенности, достоинства и недостатки. К ЛС предъявляется ряд требований, выполнение которых обеспечивает высокую эффективность при их эксплуатации, необходимое качество связи, дальность связи.

1.2. Классификация, конструкции и частотные диапазоны направляющих систем

         По конструктивным признакам направляющие системы делятся на две группы  - системы, в которых распространение электромагнитной энергии ограничивается в поперечном  направлении  (закрытые системы) и  системы, в которых такого ограничения нет (открытые системы) (рис. 1.4, 1.5).

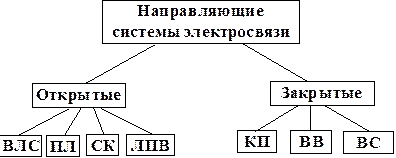
Рис. 1.5. Классификации НСЭ по конструктивным признакам

Воздушные линии связи и симметричные пары относятся к группе симметричных цепей, т.е. НС этой группы имеют два проводника с одинаковыми конструктивными и электрическими свойствами.

Направляющие системы являются основными элементами кабелей связи, они классифицируются по частотному диапазону их использования (рис. 1.6).

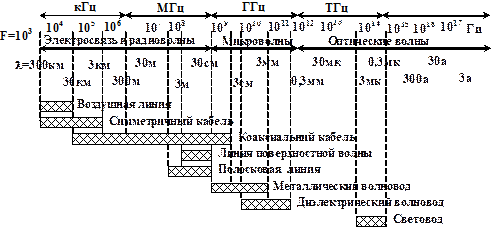
Рис. 1.6. Частотные диапазоны разных направляющих систем

Характеристики разных направляющих систем и области их применения приведены в таблице 1.1

Вопросы и задания для самоконтроля

2.     Дайте определение НС.

3.     Чем обеспечивается свойство направленности НС?

4.     Охарактеризуйте открытые НС и закрытые НС, приведите примеры этих систем.

5.     Приведите конструкции НС, охарактеризуйте их особенности, укажите область применения.

6.     Какие виды информации передаются по НС?

7.     Дайте определение канала тональной частоты.

8.     Дайте определение канала связи.

8.   Можно ли передать по ВЛС сигнал с полосой частот ?

9.     Является ли коаксиальная пара симметричной НС?

10.      Можно ли по КК передать сигнал в диапазоне частот  от 1 до 3 кГц?

11.     Возможна ли передача телевизионных сигналов по СК?

12.     Является ли направляющей системой структура стекло/полимер?

Письменные задания

1.     Запишите условие (1.1) для идеальной системы связи.

2.     Приведите электрические параметры сред.

3.     Приведите структурную схему линии связи с цифровыми и с аналоговыми сигналами в линейном тракте.

4.     Приведите структурную схему элементарного усилительного участка.

5.     Охарактеризуйте подсистемы линии связи.

6.      Объясните, как обеспечивается направленность распространения электромагнитных волн в радиолиниях, радиорелейных линиях?

7.     Охарактеризуйте особенности беспроводных ЛС.

8.     Охарактеризуйте особенности проводных ЛС.

9.     Приведите диаграмму уровней секции ОУП-ОУП.

10.      Выбрать тип НС для одновременной передачи следующих видов информации: 30 телевизионных каналов, 2 канала радиовещания.

11.      Выбрать тип НС для одновременной передачи 2 каналов ТВ,  КТЧ, 1000 каналов передачи данных.

12.      Выбрать тип НС для одновременной передачи амплитудно–модулированных (АМ) сигналов: .

13. Выбрать тип НС для одновременной передачи АМ сигналов с верхней боковой частотой:     ,   , .

2. Построение сетей электросвязи

Любая сеть связи содержит: оконечное оборудование (каналообразующую аппаратуру), линии связи, системы коммутации, оконечные устройства (устройства абонентского доступа). Обобщённая схема сети связи приведена на рис. 2.1.

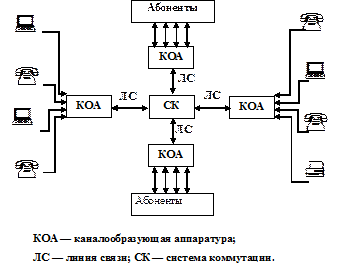
Рис. 2.1. Обобщённая схема сети связи.

Сеть связи представляется узлами (пункты коммутации) и рёбрами (линиями связи), соединяющими эти узды между собой.

Все сети связи Украины представляют Единую Национальную Сеть Связи (ЕНССУ). Сети связи строятся по иерархическому принципу – от высшей ступени к низшей, т. е. от центра (столицы) к периферии в соответствии с административно – территориальным делением государства. Территория Украины разбита на 25 зон (по числу областей), главным узлом является г. Киев. Линии связи делятся на магистральные, зоновые, внутризоновые. Магистральные линии соединяют головной узел с областными центрами (центрами зон) и центры зон между собой, они образуют магистральную сеть. Зоновая сеть организуется в пределах одной или двух соседних областей на основе зоновых  линий связи. Зоновая сеть образуется внутризоновыми и местными линиями. Местная связь состоит из сельской связи (райцентр – населённые пункты административного района) и городской телефонной сети (ГТС). Зоновая связь организуется зоновыми (внутризоновыми) линиями связи.

В процессе распространения сигналов вдоль ЛС, вследствие потерь энергии, в НС происходит постепенное уменьшение амплитуды сигнала и его искажение вследствие действия помех различного происхождения. В усилительных пунктах сигнал усиливается до необходимого уровня, а в регенерационных регенерируется и усиливается.

 ЕНССУ объединяет  сети всех уровней иерархии, строится на основе единой системы нумерации и единой системы построения каналообразующей аппаратуры. ЕНССУ делится на первичную сеть и вторичную. Первичная сеть – это совокупность всех каналов без подразделения их по назначению и видам связи. В её состав входят линии связи и каналообразующая аппаратура. Вторичная сеть состоит из каналов одного назначения, (телефонных, телевидения, передачи данных и др.), образуемых на базе первичной сети. Вторичная сеть образуется на базе первичной.

Топология сетей связи представляет структурное построение сети. Существует несколько вариантов топологий:

• полносвязная (каждый с каждым), при которой любой узел сети имеет прямые связи со всеми остальными узлами;
• узловая, при которой несколько пунктов группируются в узлы и последние соединяются между собой;
• радиальная (звёздообразная), при которой имеется один узел, который  соединяется радиальными линиями с другими пунктами.

Распространённой является топология сочетающая радиальную и узловую  структуры. В этом случае узлы одного уровня иерархии соединяются с нижестоящими узлами между собой.

В информационно – вычислительных сетях используются шинные, древовидные, решётчатые (ячеистые) структуры.

Построение городской телефонной сети (ГТС). Как любая сеть связи, ГТС должна быть высоконадёжной и экономичной. Надёжность сети обеспечивается её разветвлённостью, наличием обходных путей. Экономичность достигается минимизацией расстояний между узлами сети. ГТС организуется на основе полносвязной, радиальной, узловой и гибридной топологий. ГТС представляет совокупность станционных сооружений, линий связи, оконечных абонентских устройств, обеспечивающих возможность передачи различных видов информации.

Станционные сооружения предназначены для коммутации, а при необходимости  - для усиления и регенерации сигналов  (автоматические телефонные станции). Существует две схемы построения ГТС – районированная и нерайонированная. ГТС крупных городов строится по принципу районирования. В этом случае территория города делится на ряд районов. В каждом районе находится несколько АТС и районная АТС (РАТС). АТС и РАТС соединяются между собой по радиальной схеме. РАТС отдельных районов соединяются между собой по разным схемам: полносвязной, с узлами входящих сообщений, с узлами входящих и исходящих сообщений. Нерайонированная сеть применяется в небольших городах. В этом случае несколько АТС (2-3) соединяются между собой по полносвязной схеме.

Появление высокоскоростных систем передачи, цифровых систем коммутации и оптических кабелей в больших городах (с количеством абонентов более 1 млн.) привело к появлению комбинированных топологий на основе транспортных колец (рис. 2.2).

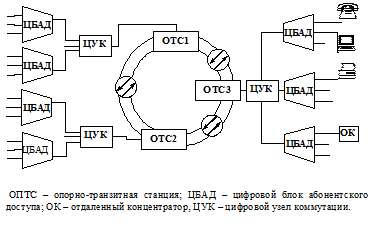
Рис. 2.2. Построение городской телефонной сети на основе транспортного кольца

Такая схема организации связи обеспечивает высокую надёжность, живучесть и экономичность сети.

Линии связи ГТС состоят из абонентских и соединительных линий. Абонентские линии – это участок сети от АТС до абонента, соединительные линии (СЛ) соединяют АТС между собой, а также АТС с междугородной телефонной станцией.

Построение сетей абонентских линий осуществляется несколькими способами: по бесшкафной и шкафной  системам. Примером бесшкафной системы является система непосредственного включения абонентских линий в соответствующую аппаратуру АТС. Такая система применяется на сетях малой ёмкости.

Схема шкафной системы приведена на рис. 2.3.

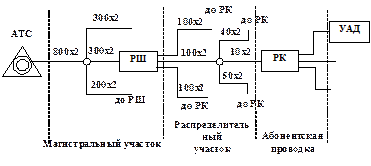
Рис. 2.3. Шкафная система построения  абонентских линий

В этом случае линия от АТС до распределительных шкафов (РШ) называется магистральной, от шкафов до распределительных коробок (РК) – распределительным участком, от распределительных коробок  до абонентских устройств – абонентской проводкой.

Кроме этих  схем при длине АЛ до 0,5 км применяются схема прямого включения (рис. 2.4).

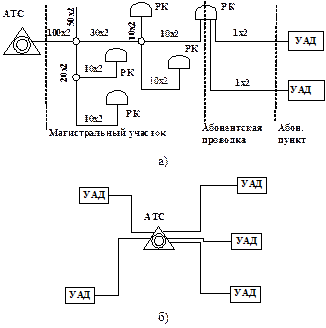
Рис. 2.4. Построение абонентской линии по принципу прямого включения

В шкафной системе территория обслуживания АТС делится на шкафные районы, подключения абонента осуществляется через РШ и РК. От АТС  до РШ прокладываются в разных направлениях кабели большой ёмкости, далее они разветвляются на кабели меньшей ёмкости, которые подключаются к РШ, далее от РШ до РК ёмкость кабелей также уменьшается.

Вопросы и задания для самоконтроля

1. Назовите составляющие сети связи, объясните их назначение.

2. Что представляют узлы и ребра сети связи?

3. Дайте определение ЕНССУ.

4. Дайте определение первичной, вторичной, транспортной сетей.

5. Дайте определение магистральной, зоновой, местной сети.

6. Какие требования предъявляются к ГТС, чем они обеспечиваются?

7. Какие устройства входят в состав ГТС?

8. Перечислите схемы построения ГТС, охарактеризуйте их.

9. Поясните структуру абонентской линии.

10. Охарактеризуйте шкафную систему построения ГТС, какое преимущество этой системы.

Письменные задания

1. Приведите иерархическую структуру сети связи, охарактеризуйте её.

2. Приведите схемы следующих топологий: полносвязной, радиальной, радиально – узловой, ячеистой (сетчатой), древовидной. Сравните эти топологии.

3. Составьте схему построения районированной и нерайонированной ГТС.

4. Приведите схемы межстанционных соединений ГТС: «каждая с каждой», с УВС, с УВС и УИС. Сравните эти схемы.

5. Составьте схему АЛ с прямым питанием.

6. Опишите схему организации связи на основе транспортного кольца.

7. Приведите структуру сельской сети связи.

8. Рассчитать длину усилительного участка АСП с линейным спектром частот 500…..20000 кГц. Усилительная способность системы передачи . Затухание кабеля на частоте 1 МГц составляет  3 дБ/км.

9. Рассчитать длину регенерационного участка для системы передачи ИКМ – 480. Недостающие данные взять из задачи 8.

10. Определить количество пар на магистральном участке кабеля, если ёмкость АТС составляет 1000 номеров, в зоне прямого питания находится 100 абонентов, в резерве оставлено 5% номеров АТС, эксплуатационный запас кабеля составляет 10%. АТС обслуживает 3 шкафных района с количеством абонентов в 1 – ом районе 300, во втором – 400. Все номера АТС, кроме резервных задействованы. Привести схему сети.

3. Кабели на основе направляющих систем

3.1. Электрические кабели

         Кабель – электротехническое изделие, содержащее совокупность направляющих систем, объединенных в одну конструкцию. Кабель имеет общую металлическую оболочку и защитные покровы. Каждая пара проводов образует электрическую цепь. Современные кабели связи классифицируются по ряду признаков.

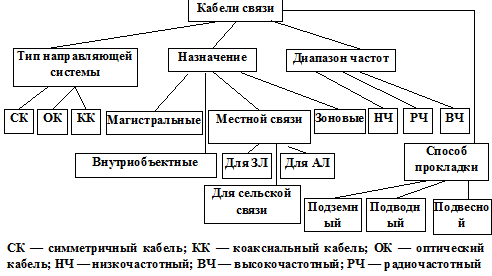
Рис. 3.1. Классификация кабелей связи

         Кроме этого кабели классифицируются по типу изоляции, способу скрутки, материалу оболочек, типу броневых покровов. Симметричный кабель содержит симметричные пары с одинаковыми электрическими и конструктивными параметрами. Коаксиальный кабель содержит одну или несколько коаксиальных пар, которые могут отличаться конструктивно.

         Основные конструктивные элементы кабеля:

• изолированные проводники (жилы) в СК;
• коаксиальные пары (в КК);
• защитные оболочки;
• броневые покровы.

         Проводники кабелей связи должны иметь малое электрическое сопротивление, достаточную гибкость, механическую прочность. Они изготавливаются из меди или алюминия, могут быть сплошными и многожильными, а также биметаллическими. В КК используются ленточные, гофрированные проводники и оплётка (рис 3.2, рис. 3.3).

         Изоляция проводников должна иметь большое электрическое сопротивление, большую электрическую прочность (пробивное напряжение). Практически идеальным диэлектриком является воздух, у которого , , . Изоляция в кабелях связи чаще всего комбинированная и содержит диэлектрик и воздух. Диэлектрик фиксирует взаимное расположение проводников вдоль линии. Для изоляции применяется такие диэлектрики: полиэтилен, полистирол (стирофлекс), фторопласт, в коаксиальных кабелях – специальная керамика. В низкочастотных кабелях используется также кабельная бумага. В кабелях связи используется такие виды изоляции: трубчатая, кордельная (кордельно-бумажная и кордельно-стирофлексная), сплошная и пористая, баллонная, шайбовая (рис. 3.4).

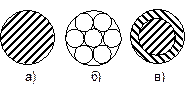
Рис. 3.2. Конструкции кабельных проводников: а) сплошной; б) гибкий; в) биметаллический

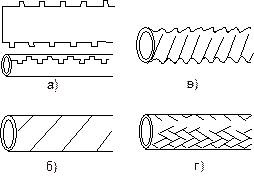
Рис. 3.3. Конструкции внешних проводников коаксиальных кабелей:

а) с продольным швом типа «молния»; б) гофрированный; в) ленточный; г) оплётка

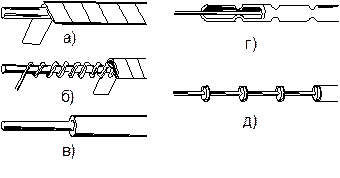
Рис. 3.4. Типы изоляций кабелей связи

         Защитные оболочки герметизируют кабель, выполняются из полиэтилена, поливинилхлорида, свинца, алюминия, стали.

         Броневые покровы накладываются поверх оболочек и предохраняют кабель от возможных повреждений.

         Существуют две разновидности брони:

• стальные ленты, намотанные на сердечник кабеля с перекрытием 1,5;
• повив из круглых стальных проволок.

         Применение того или иного вида брони или её отсутствие определяется условиями прокладки кабеля.

         Типы скруток и строение сердечника кабеля. Жилы в кабеле обычно скручиваются в элементарные группы. При скрутке создаются одинаковые условия для всех пар в кабеле относительно внешних и внутренних влияний, обеспечивается гибкость кабеля, что необходимо при его прокладке. Наиболее распространённые типы скруток:

• парная;
• звёздная (четвёрочная);
• двойная звёздная.

         Жилы кабеля скручиваются с определённым шагом в элементарной группе, группы уже с другим шагом скручиваются между собой.

         Скрученные в группы изолированные жилы образуют сердечник кабеля. Существуют две основные системы построения сердечника:

• пучковая (проводники образуют пучки, а пучки – сердечник кабеля)
• повивная (проводники располагаются в сердечнике повивами вокруг центрального проводника или кордом)

         Скрутка однородная, если все группы одинаковая и неоднородная, если сердечник имеет различные группы, а также разные направляющие системы (коаксиальные и симметричные пары).

         Кабельная скрутка обматывается поясной изоляцией из кабельной бумажной ленты, поверх которой наносятся защитные и броневые покровы. Общий вид кабеля приведен на рис. 3.5.

Рис. 3.5. Общий вид кабеля с защитным покровом

         Маркировка кабелей – это определенная система условных обозначений, которые отражают основные классификационные признаки и конструктивные особенности кабелей.

 Маркировка СК имеет вид:

1 2 3 4 5 6 – n x m x d,

где на позициях 1-3 обозначается тип кабеля, позиция 4 отображает тип изоляции токоведущих жил, 5 – тип защитной оболочки, 6 – тип брони, n – количество элементарных групп, m -  количество жил в группе, d – диаметр проводника в группе.

Кабели маркируются следующим образом:

  МК – высокочастотный кабель;

  ЗК – зоновый  ВЧ кабель;

  КС – высокочастотный кабель сельской связи;

  ТЗ – телефонный звёздной скрутки;

  Т – телефонный.

Маркировка изоляции:

  С – стирофлексная кордельная;

  П – полиэтиленовая;

  В – поливинилхлоридная;

  А – алюминиевая;

  С – стальная;

  Бумажная ленточная и бумажная изоляция в маркировке кабеля кордельная  не обозначается.

Маркировка защитных оболочек и покровов:

  П – полиэтиленовая;

  В – поливинилхлоридная;

  А – алюминиевая;

  С – стальная.

Свинцовая оболочка в маркировке не обозначается.

Маркировка броневых покровов:

  Г – голый  без брони;

  Б – броня из плоских стальных лент;

  К – броня из круглых проволок.

Алюминиевые и стальные оболочки для предотвращения от действия коррозии покрываются полиэтиленовыми или полихлорвиниловым шлангом, обозначается как или . Поверх брони обычно накладывается защитный джутовый покров, который в маркировке не обозначается. Если кабель имеет экран, то это обозначается буквой «Э».

Пример: симметричный кабель МКСАШ_П –

В коаксиальных кабелях обозначается:

• тип кабеля;
• тип защитной оболочки;
• тип брони;
• количество коаксиальных пар.

Типы коаксиальных кабелей:

• КМ – коаксиальный магистральный;
• МКТ – малогабаритный коаксиальный, телефонно – телевизионный;
• ВК – однокоаксиальный.

Пример: КМГ – 4; МКТСБ – 4

3.2. Оптические кабели

Направляющей системой оптического кабеля (ОК) является волоконный световод (ВС). Требования к ОК обусловлены условиями его прокладки и эксплуатации. Конструкция ОК должна обеспечивать его прочность в процессе прокладки, монтажа и эксплуатации, предохранять ВС от растягивающих продольных усилий, возникающих при прокладке кабеля.

         Конструктивные элементы ОК:

• модуль волоконно–оптический (МВО);
• силовые и армирующие элементы;
• заполняющие элементы;
• защитные покровы;
• броневые покровы;
• жилы дистанционного питания.

МВО – это полиэтиленовая трубка, в которой свободно уложены 1, 2 или 4 волоконных световода (рис. 3.6).

Рис. 3.6. Модуль волоконно – оптический

Базовыми конструкциями ОК являются конструкции (рис. 3.7):

• с повивной скруткой;
• ленточные.

Рис. 3.7. Базовые конструкции оптических кабелей

В кабеле с повивной скруткой в центре находится центральный силовой элемент, предохраняющий кабель от продольного растяжения в процессе прокладки, он выполняется из стеклопластика или в виде стального тросика. Вокруг ЦСЭ располагается повив из шести МВО. В ОК с небольшим числом ОВ часть модулей может быть заменена полимерными заполнителями (корделями).

Расположение остальных элементов такое же, как  и в электрических кабелях. В ОК не используются свинцовые оболочки, чаще всего применяются тонкие стальные или алюминиевые гофрированные оболочки с защитными полимерными покрытиями. Броня в ОК может быть выполнена из стеклостержней  (обозначается «С») или в виде оплётки (обозначается «О»). Большинство современных ОК не имеют жил дистанционного питания. Всё свободное пространство в  ОК для его герметизации заполняется гидрофобным заполнителем.

Пример маркировки оптических кабелей

маркоразмер
марка
тип
вид
ОКЛБг–Н–3–ДА13–3 4Е–0,40Ф3,5/0,30Н19–12/0
1	2	3	4	5	6	7	8	9
номер позиции

1.     Вид кабеля – Оптический Кабель – ОК

2.     Область использования – Линейный (для магистральных, Зоновых и городских сетей связи) – Л

3.     Тип брони – Бг (гофрированная стальная лента, наложенная продольно)

4.     Шланг выполнен из материала Нераспространяющего горение – Н

5.     Номер разработки – 3

6.     Тип силовых элементов и защитных покровов. Силовые элементы – центральный силовой элемент (ЦСЭ) – Диэлектрический (стеклопластиковый) стержень и высокомодульные Арамидные нити –ДА. Тип защиты покровов – 13 (оболочка и шланг из пластмасс, нераспространяющих горение, броня – сталь)

7.     Структура построения сердечника оптического кабеля (ОК). [Количество оптических модулей (ОМ) в ОК] х [Количество оптических волокон (ОВ) в ОМ] – 3х4. Тип оптического волокна – одномодовое, соответствующее рекомендации G.652 ITU–Т   –  Е

8.     Оптические характеристики ОВ. [Максимальный индивидуальный коэффициент затухания (МИКЗ) на длине волны 1310 нм (ф) – 0,40 дБ/км и коэффициент хроматической дисперсии на этой длине волны – 3,5 пс/(нм•км)] / [МИКЗ на длине волны 1550 нм (н) – 0,30 дБ/км и коэффициент хроматической дисперсии на этой длине волны – 19 пс/(нм•км)]

9.     [Общее количество ОВ в кабеле – 12 (двенадцать)] / [количество жил дистанционного питания (ДП) в кабеле – 0 (ноль)]

Пример приведен для случая использования в кабеле одномодового оптического волокна. В случае использования в кабеле с аналогичной конструкцией многомодовых оптических волокон позиции номер семь и восемь условного обозначения кабеля изменять свой вид.

Например, если в кабеле используется многомодовое  ОВ (G.651   ITU–T), работающее на длине волны 850 нм и имеющее, например: МИКЗ–3,0 дБ/км и ширину полосы пропускания не менее 500 МГц•км, то условное обозначение кабеля примет вид:

                      ОКЛБг–Н–3–ДА13–3 4М–3,ОВ500–12/0

Вопросы и задания для самоконтроля

1. Дайте определение кабеля связи.

2. По каким признакам классифицируются кабели связи:

3. Назовите конструктивные элементы кабелей связи.

4. Какие требования предъявляются к проводникам и изоляции токоведущих жил?

5. Какие требования предъявляются к кабелям связи?

6. Какое назначение броневых покровов и защитных оболочек?

7. Какие кабели применяются для магистральной, зоновой и местной связи?

8. Объясните особенности конструкции оптических кабелей.

9. Объясните маркировку оптических кабелей.

Письменные задания

1. Приведите эскизы проводников симметричных и коаксиальных кабелей.

2. Приведите эскизы защитных и броневых покровов.

3. Приведите эскизы коаксиальных пар с разными типами изоляции.

4. Приведите поперечные сечения различных скруток СК: парной, звёздной, двойной парной, двойной звёздной. Объясните необходимость скрутки проводников в кабеле.

5. Приведите эскизы поперечных сечений кабелей: – 7 x 4 x 1.2; МКТБ – 4, ЗКП – 4 x 1.2, ТЗПП – 4 x 1.2, . Укажите  все конструктивные элементы, область применения, способ прокладки.

6. Приведите эскиз поперечного сечения оптических кабелей ОКЛБ –

7. Обоснуйте выбор кабеля для линии связи Киев – Львов для передачи 10000 КТЧ.

8. Обоснуйте выбор кабеля соединительной линии ГТС для передачи 100 КТЧ.

9. Обоснуйте выбор типа кабеля для распределительной сети ГТС

10. Сколько пар в кабеле ТПП повивной скрутки, если в центральном повиве 4 пары всего повивов 12.

4. Электродинамика направляющих систем

4.1. Общие положения

Строгое решение задачи распространения электромагнитной энергии по направляющим системам, образующим разнообразные кабели связи требует применения средств электродинамики и решения уравнений Максвелла. Методы электродинамики позволяют решить все задачи передачи, излучения, поглощения в любой направляющей системе и в любом частотном диапазоне. НС имеет достаточно сложную структуру, поэтому их при анализе вводится ряд допущений и процесс распространения энергии разбивается на независимые процессы:

• передачу;
• излучение;
• поглощение.

Каждый из этих процессов определяет те или иные свойства НС. При анализе НС параметры среды усредняются по объему, среда обладает следующими свойствами:

• изотропностью, т.е
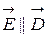
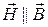
• линейностью, т.е. ;
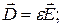
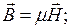
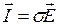• однородностью, т.е. параметры среды не зависят от координаты.

При анализе НС анализируются гармонические колебания, т.к. сигнал любой формы может быть представлен суперпозицией гармонических составляющих в виде ряда Фурье.

Уравнения Максвелла (первое и второе) обобщают основные законы электродинамики: закон полного тока и электромагнитной индукции. Уравнения записываются в интегральной (4.1) и дифференциальной форме (4.2).

; (4.1) 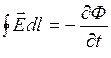; ; 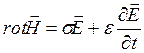(4.2) 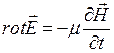. Для гармонических колебаний справедливо 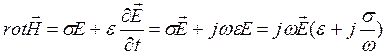(4.3)

Обозначим 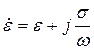, где - комплексная диэлектрическая проницаемость, соотношение мнимой и действительной частей которой определяет свойства среды:

- проводник;

- диэлектрик.

Кроме уравнений (4.1) и (4.2) используются уравнения (4.3) и (4.4).

; (4.4)

Уравнения (4.4) означают, что электрическое поле имеет заряды, а магнитные заряды не существуют. Силовые линии электрического поля начинаются и заканчиваются на зарядах, от зарядов они расходятся (или сходятся) в окружающее пространство. Силовые линии магнитного поля всегда направлены по нормали к металлическим поверхностям, линии магнитного поля параллельны к проводящим поверхностям. В соответствии с (4.2) изменяющееся во времени магнитное поле порождает переменное электрическое поле и наоборот. Процесс распространения электромагнитного поля поясняется на рисунке 4.1.

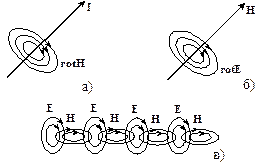
Рисунок 4.1. Распространение электромагнитного поля

4.2. Энергетические соотношения для электромагнитного поля

Рассмотрим баланс энергии электромагнитного поля. Запас энергии в объеме определяется суммой электрической и магнитной энергии:

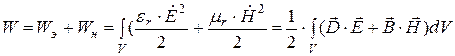(4.5)

где первое слагаемое – энергия электрического поля, а второе – магнитного. Это выражение аналогично известной формуле для колебательного контура:

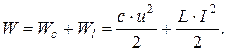
Используя выражение Максвелла можно получить выражение:

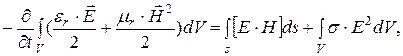(4.6)

где ds – элемент поверхности, ограничивающий объем V.

Это выражение известно как теорема Умова-Пойтинга. Левая часть выражения характеризует расход электромагнитной энергии в единицу времени. Первое слагаемое правой части представляет поток энергии в единицу времени через замкнутую поверхность S объема V в окружающее пространство. Энергия, распространяющаяся в единицу времени через поверхность, перпендикулярную направлению потока энергии, определяется величиной называется вектором Пойнтинга. Второе слогаемое определяет энергию внутри объема, которая преобразовалась в тепло.

Изменение запаса энергии, находящейся в некотором объеме V, происходит за счет расхода энергии внутри объема и распространения ее за пределы этого объема. Теорема Умова-Пойнтинга устанавливает связь между напряженностями полей Е и Н на поверхности какого-либо объема с потоком энергии, входящей в объем или выходящей из него. Зная величины Е и Н на поверхности НС можно определить поглощаемую и распространяющуюся электромагнитную энергию.

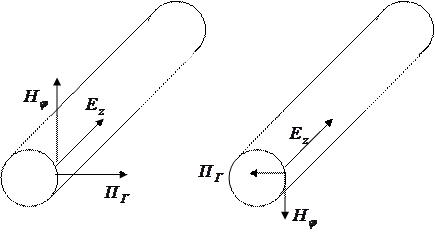
Рассмотрим одиночный проводник в полярной системе координат. Составляющие электромагнитного поля на его поверхности формируют вектор Пойнтинга, который можно разложить на составляющие, определяющие распространение энергии вдоль линии и в направлении перпендикулярном к проводнику (излучение, тепловые потери).

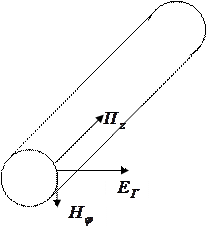а) б) в)

Рис. 4.2 – Составляющие вектора Пойнтинга: а) распространение, б) излучение, в) поглощение.

Продольная составляющая П_r определяет распространение энергии вдоль линии. Радиальная составляющая определяет излучение энергии в свободное пространство, в СК и КК она обуславливает взаимные влияния. Эта же составляющая, направленная внутрь проводника определяет тепловые потери.

Приведенный анализ позволяет сделать важный вывод: в НС энергия распространяется в пространстве ограниченном проводниками, проводники только направляют энергию в нужном направлении. Если к проводникам линии подключить генератор, то между проводниками возникнет переменное электромагнитное поле. Это поле, окружая проводники, движется вдоль них со скоростью, близкой к скорости света. Одновременно по линии протекает ток. Напряженность электрического поля Е соответствует напряжению U, а напряженность магнитного поля – току І.

Рис. 4.3 – Токи протекающие (I_пр) и токи смещения (I_см): а) в кабеле; б) в конденцаторе; в) в атмосфере; г) в волноводе.

Непрерывность тока, протекающего по линии обеспечиваются протеканием тока проводимости в проводниках и тока смещения в диэлектрике (как это происходит в конденсаторе). В различных НС и в различных частных диапазонах преобладают или токи смещение или токи проводимости.

Вопросы и задания для самоконтроля

1.    Какие процессы возникают при распространении электромагнитной энергии?

2.     Какие допущения принимаются при анализе НС?

3.     Объясните смысл первого и второго уравнений Максвелла.

4.     Объясните смысл третьего и четвертого уравнений Максвелла.

5.     Что такое ток смещения? Приведите примеры возникновения тока смещения.

6.     Объясните процесс распространения электромагнитной энергии.

7.     Объясните смысл уравнения 4.4.

8.     Объясните смысл уравнения 4.5.

9.     Дайте определение вектора Пойтинга, объясните физический смысл его составляющих.

10.           Какое назначение проводников в направляющей системе?

Письменные задания

1.     Определить, при какой частоте грунт с удельным сопротивлением r=100 Ом×м/мм² приобретет свойства проводника, e_r=2,5.

2.     Определить, при какой частоте медный проводник с удельным сопротивлением r=0,0175 Ом•мм²/м приобретет свойства диэлектрика.

3.     Получить выражения для радиальной и продольной составляющих вектора Пойнтинга.

4.     Доказать, что тангенциальной составляющей вектора Пойнтинга не существует.

5.     Цепь содержит источник и последовательную RC -цепь. Обозначьте на схеме такой цепи токи проводимости и токи смещения.

6.     Изобразите процесс распространения электромагнитного поля в свободном пространстве, укажите место тока смещения.

7.     Укажите путь токов проводимости и смещения в волноводе.

8.     Какие составляющие вектора Пойнтинга преобладают в кабеле, в антенне?

9.     Объясните, какой ток (проводимости или смещения) преобладает в проводной НС, в волноводе.

10.   Какой ток (проводимости или смещения) существует в ВС?

4.3. Режимы передачи по направляющим системам

В зависимости от используемых длин волн и среды распространения электромагнитной энергии выделяется пять различных режимов передачи.

Статический режим относится к процессам электростатики и магнитостатики, характеризуется отсутствием временной зависимости поля. Уравнения Максвелла имеют вид:

На основе уравнений электростатики определяется емкость проводников по формуле :

С=Q/U.

Стационарный режим относится к случаю передачи по проводникам постоянного тока І=s×Е, который создает магнитное поле, электрическое поле при этом не индукцируется и уравнения Максвелла имеют вид:

Магнитное поле имеет вихревой характер, а электрическое – безвихревой (потенциальный). В этом режиме определяется индуктивность цепи L=Ф/І, где Ф - магнитный поток, пронизывающий цепь. Для анализа процессов применяются законы Ома, Кирхгофа.

Квазистационарный режим охватывает диапазон до 10¹⁰ Гц, в этом режиме индуцируется вихревое электрическое поле, вызванное изменением электрического поля. Уравнения Максвелла имеют вид:

В этом режиме l>>D, где D – обобщенный поперечный размер НС, l - длина волны, токи смещения еще незначительны. Для анализа процесов используются законы Ома, Кирхгофа, телеграфное уравнение, волновое уравнение.

Электродинамический режим относится к области высоких частот и коротких волн (l £ D, F » 10¹⁰¸10¹² Гц). При анализе решают волновые уравнения. Уравнения Максвелла имеют вид:

Т.е. в этом режиме токами смещения пренебрегать нельзя.

Волновой и квазиоптический режимы характерны для процессов в диэлектрике, когда доминирующими являются токи смещения, а токи проводимости незначительны. В этом случае , , и Гц. При анализе процессов используются законы оптики (Гюйгенса, Френеля) и решаются волновые уравнения.

Приведенная классификация режимов характеризует универсальность уравнений Максвелла, единство законов электродинамики.

4.4. Классы и типы волн в НСС

Характер распространения электромагнитных волн в НС определяется структурой поля в ней. Эта структура определяет возможность того или иного спектра частот, что и обуславливает свойства направляющей системы. Распространяющиеся в НС волны делятся на классы и типы. Класс волны определяет наличие продольных составляющих поля ( и ). В общем случае структура поля имеет по три составляющих электрического и магнитного полей. В конкретных системах некоторые из этих составляющих обращаются в нуль. Существуют следующие классы волн:

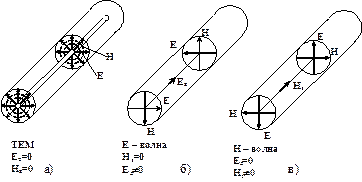
Т – поперечно-электромагнитная ТЕМ-волна ( );

Е – электрическая или поперечно-магнитная ТМ-волна ( );

Н – магнитная или поперечно-электрическая ТЕ-волна ( );

ЕН и НЕ – смешанные гибридные волны ( ).

Рис. 4.4 – Типы волн в направляющих системах

ТЕМ-волны содержат толко поперечные составляющие поля, т.е. силовые линии поля целиком лежат в поперечных плоскостях и в точности повторяют картину силовых линий статического и стационарного режимов. Эта волна существует лишь в линиях, содержащих два изолированных проводника, находящихся под разными потенциалами. Эта волна является основной в проводных НС, характеризуется токами проводимости и практически нулевыми токами смещения.

Волны Е и Н кроме поперечных составляющих содержат по одной продольной составляющей поля. Силовые линии этих волн располагаются как в поперечном, так и в продольном сечениях НС. Эти волны возбуждаются в однопроводных линиях (волноводах). По поперечному сечению НС должно уложиться целое число полуволн (не менее одной).

Гибридные волны содержат шесть компонент поля, в том числе и продольные составляющие и . Такие волны возбуждаются в световодах и диэлектрических волноводах.

Классы волн делятся также по типам. Модам тип волны или мода определяется сложностью структуры поля в поперечном сечении НС, т.е. числом максимумов и минимумов поля в этом сечении.

Мода – это самосогласованное распределение поля, которое сохраняется при распространении волны вдоль НС, не содержащей неоднородностей. Число распространяющихся мод в НС бесконечно, эти волны отличаются наличием тех или иных составляющих поля, а, следовательно, и его структурой. Различают основной тип волны и волны высших типов. Основная мода имеет простейшую структуру. В двухпроводных НС основной является ТЕМ-волна. Типы волн обозначаются двумя числовыми индексами n и m, которые означают число полных изменений (вариаций) поля по поперечным координатам.

Вопросы и задания для самоконтроля

1.     Назовите режимы передачи по НС.

2.     Охарактеризуйте каждый режим передачи.

3.     В каком режиме передачи используются симметричный кабель, коаксиальный кабель, световод?

4.     Чем определяется наличие тока смещения в НС?

5.     Дайте определение класса волны.

6.     Охарактеризуйте классы электромагнитных волн.

7.     Дайте определение типа волны (моды).

8.     Дайте определение основного типа волны.

9.     Чем определяется длина волны основной моды в волноводе?

10.           Какие классы волн распространяются в волноводах и световодах?

Письменные задания

1.     Заполните приведенную ниже таблицу

Режим передачи	Левая часть уравнения Максвелла	Правая часть			Частота, Гц; соот-ношение D и l	Тип волны	НС для режима
		Металл	Диэлектрик
Статичес-кий
Стационар-ный
Квазиста-ционарный
Электроди-намический
Волновой и квази-оптический

  2. Изобразите структуру ТЕМ-волны в:

X

Y

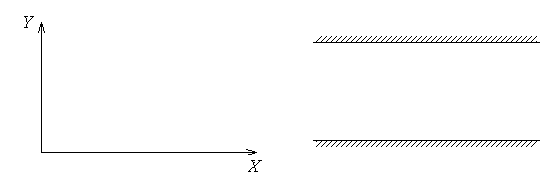
а) свободное пространство; б) проводящие плоскости.

3.     Изобразите преобразование 2-х проводящих плоскостей и линии поля для следующих структур:

а) преобразование в б) преобразование в

коаксиальную цепь; симметричную цепь.

4.    Прямоугольный волновод имеет размеры 2´4 см. Могут ли в нем распространяться гармонические колебания с частотой 10 МГц?

5.     Определить типы НС, если:

a)

б)

в)

г)

6. Волновод имеет поперечные размеры 1´3 см. По волноводу распространяются моды с l=1,5 см; l=3 см; l=1 см; l=0,5 см. Какие из этих мод являются модами высшего порядка?

4.5. Электромагнитные процессы в проводниках и диэлектриках

Физические среды отличаются своими электромагнитными свойствами. Металлы и диэлектрики существенно отличаются проводимостью. Для упрощения анализа НСС часто используется понятие идеального проводника ( ) и идеального диэлектрика ( ). В идеальном проводнике существует только ток проводимости , а в идеальном диэлектрике – только ток смещения .

Металлы практически во всех диапазоне частот являются проводниками, в диэлектриках (полиэтилен, полистирол и др.) на всех частотах преобладают токи смещения. Естественные среды (почва, вода, лёд) обнаруживают свойства проводников в области низких частот, а в области высоких частот действуют как диэлектрики. Потери электромагнитной энергии в при распространении в диэлектриках незначительные. Скорость распространения электромагнитной энергии в диэлектрике определяется , где км/с – скорость света в свободном пространстве. При распространении плоской волны в диэлектрике и взаимно перпендикулярны, а отношение Е к Н определяет сопротивление среды распространяющейся волне, т.е. волновое сопротивление . Волновое сопротивление свободного пространства Ом, а волновое сопротивление диэлектриков определяется

Если по проводнику протекает переменный ток, то в нем возникает поверхностный эффект (скин-эффект), сущность которого ясна из рисунка 4.5.

Рис. 4.5 – Явление поверхностного эффекта: а) линия тока, магнитного поля и вихревых токов; б) деление токов; в) вытеснение тока на край проводника

Вследствие поверхностного эффекта ток с ростом частоты вытесняется на края проводника, т.е. протекает только по поверхности проводника, что приводит к увеличению его сопротивления при увеличении частоты. Переменный ток распространяется по сечению проводника неравномерно и затухает пропорционально , - коэффициент затухания в металле. Поверхностный эффект характеризуется эквивалентной глубиной проникновения. Эквивалентная глубина проникновения Q - это такая глубина проникновения поля в проводник, при которой напряженность поля (или плотность тока) уменьшается в =2,718 раз.

,

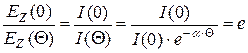тогда 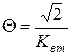, - коэффициент вихревых токов.

При увеличении частоты глубина проникновения уменьшается, т.е. поверхностный эффект с ростом частоты возрастает. Поверхностный эффект в большей степени проявляется в проводниках с большим удельным сопротивлением.

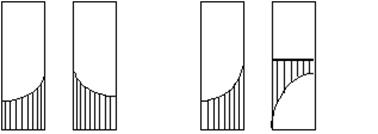
С поверхностным эффектом связаны эффект близости и эффект действия окружающих масс. Эффект близости проявляется в симметричной паре (рис. 4.6). В этом случае происходит перераспределение плотности токов в проводниках.

Рис. - 4.6 – Эффект близости в симметричной паре.

В кабеле всегда располагается несколько симметричных пар, есть другие металлические элементы. В этом случае возникает перераспределение электромагнитных полей, приводящее к изменению распределения плотности токов, что также увеличивает сопротивление цепи.

Контрольные вопросы

1.     Объясните сущность поверхностного эффекта.

2.     Объясните зависимость сопротивления проводника от частоты.

3.     Что такое глубина проникновения?

Письменные задания

1.     Запишите выражение для сопротивления проводников воздушной линии связи и витой пары.

2.     Как отличается глубина проникновения в стальном проводнике по сравнению с медным ?

4.6. Уравнение однородной линии

Качество передачи по линейным цепям и их электрические свойства полностью определяются параметрами этих цепей - параметрами передачи, которые делятся на две группы - первичные и вторичные. По физической природе параметры цепей, образованных НС аналогичны параметрам колебательных контуров, составленных из элементов . В контурах эти параметры являются сосредоточенными, а в цепях связи они равномерно распределены по всей длине линии. Эти параметры являются погонными, т. е. определяются на длину линии в 1 км. Сопротивление R и индуктивность L являются продольными параметрами, они включены последовательно. Ёмкость C и проводимость изоляции G – поперечные параметры, они включены параллельно. Следует отметить, что индуктивность цепи определяется двумя составляющими – внешней и внутренней, т.е. . Внешняя индуктивность определяется только геометрией направляющей системы и не зависит от частоты, а внутренняя – поверхностным эффектом и с ростом частоты уменьшается.

Вторичные параметры передачи: затухание цепи , постоянная распространения , волновое сопротивление , постоянная фазы , скорость распространения энергии . Эти параметры полностью определяются первичными параметрами.

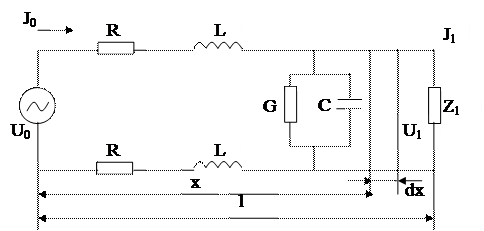
Рис. 4.6 – Схема двухпроводной цепи

На приведена эквивалентная схема двухпроводной однородной линии с первичными параметрами . В начале цепи включён генератор с выходным сопротивлением , а в конце линии нагрузка . Обозначим ток и напряжение в начале линии , в конце - .

Выделим на расстоянии х от начала линии бесконечно малый участок dx, через элемент dx протекает ток I, напряжение между проводниками на участке dx и обозначим U.

Падение напряжения на участке dx равно

. (4.7)

Утечка тока на этом участке

. (4.8)

Для решения этих уравнений исключим неизвестную величину I, продифференцировав (4.7) и, используя (4.8) :

;

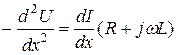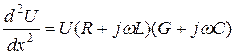, (4.9)

обозначив , получим уравнение :

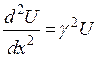. (4.10)

Решение этого уравнения имеет вид: . (4.11)

Дифференцируя (4.11) получим выражение для тока :

. (4.12)

Подставим (4.12) в (4.7), получим выражение:

. (4.13)

Введём обозначение получим систему уравнений с двумя неизвестными:

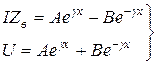. (4.14)

Для определения постоянных А и B воспользуемся значениями тока и напряжения в начале цепи (при x=0), тогда система (4.14) примет вид:

.

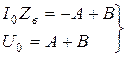Определим постоянные интегрирования

.

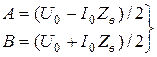Подставляя A и B в (4.14) получим

;

.

Произведя соответствующие преобразования получим значения напряжения и тока в любой точке цепи x:

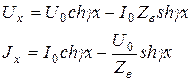(4.15)

Выражения (4.15) позволяют определить напряжение и ток в начале цепи (x=0) и в конце цепи (x=l), они устанавливают взаимную связь токов и напряжений с параметрами и . Эти уравнения справедливы при любых нагрузках и на концах цепи.

Линия называется однородной, если её первичные параметры не изменяются вдоль длины, и согласованной, если на концах она нагружена на сопротивление, равное волновому. При согласованных нагрузках и уравненя (4.15) имеют вид:

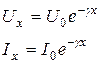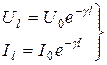; ; (4.16)

на практике, учитывая, что мощность (4.16) удобно использовать в виде:

; .

Распространение энергии по линии, ток и напряжение в любой точке цепи определяются её волновым сопротивлением и постоянной распространения.

Волновое сопротивление – это сопротивление, которое встречает электромагнитная волна при распространении вдоль однородной линии без отражения, согласованной на концах ( ). Волновое сопротивление зависит от первичных параметров цепи и частоты.

Волновое сопротивление характеризует количественное соотношение между волной напряжения U (напряженностью электрического тока E) и волной тока (напряжённостью магнитного поля H), т.е. или 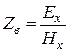. При определении волнового сопротивления рассматривается только падающая волна, т. е. отражённая волна отсутствует. Появление в линии каких-либо неоднородностей приводит к изменению структуры поля в этом сечении, изменению векторов и , а, следовательно, к изменению в этом сечении, появлению отражённых волн.

Волновое сопротивление цепи в общем случае рассчитывается по формуле

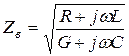. (4.17)

В однородной линии величина постоянна в любой точке цепи, и в диапазоне используемых в конкретной НС частот практически не зависит от частоты.

В общем случае является комплексной величиной и носит емкостной характер.

Коэффициент распространения является комплексной величиной и представляется в виде :

. (4.18)

Теперь 4.16 имеют вид:

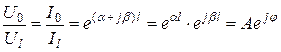. (4.19)

Модуль (4.19) определяет уменьшение абсолютного значения тока или напряжения вдоль линии. Угол характеризует изменение фазы тока или напряжения вдоль линии.

Коэффициент затухания. Электромагнитная волна, распространяясь вдоль линии уменьшается по амплитуде от генератора к нагрузке, что объясняется потерями энергии в цепи. Как следует из (4.16) мощность, амплитуда тока и напряжения уменьшаются вдоль линии по экспоненциальному закону (рис. 4.7).

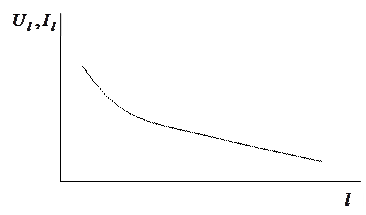
Рис. 4.6. Характер изменения мощности тока и напряжения вдоль линии

Различают два вида потерь - в проводнике и в диэлектрике. В проводнике возникают тепловые потери, в диэлектрике энергия расходуется на его поляризацию диэлектрика. Оба вида потерь возрастают с ростом частоты.

Потери в линии характеризуются коэффициентом затухания , выражение для которого можно получить из (4.18):

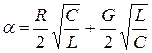. (4.20)

Действительная часть коэффициента распространения показывает уменьшение электромагнитной энергии в конце линии по сравнению с её началом

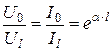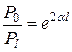; . (4.21)

Логарифмируя обе части выражений (3.15) получаем:

; .

Затухание цепи обычно представляется в децибелах (дБ) (при использовании десятичных логарифмов) или в неперах (при использовании натуральных логарифмов).

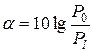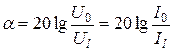; (дБ);

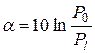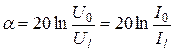; (Нп).

Между децибелами и неперами выполняется соотношение

1 Нп=8.686 дБ; 1 дБ=0.115 Нп.

Затухание является погонным параметром, измеряется на длину линии

1 км (дБ/км), с ростом частоты затухание возрастает.

Коэффициент фазы характеризует изменение фазы волны или напряжения при распространении электромагнитной волны вдоль линии, является погонным параметром, измеряется в радианах (рад/км) или градусах (град/км), определяется из (4.18):

. (4.22)

Скорость распространения энергии по цепям связи. Электромагнитная энергия распространяется по цепям связи с определенной скоростью и зависит от первичных параметров линии, определяется выражением .

Таким образом, затухание цепи определяет качество и дальность связи, а коэффициент фазы – скорость движения энергии вдоль линии.

Кроме скорости распространения энергии при анализе используются понятия фазовой и групповой скоростей. Фазовая скорость определяет скорость движения поверхности равных фаз в НС (или скорость движения волнового фронта); групповая скорость при передаче сигналов определяет скорость распространения максимума огибающей группы составляющих сложного сигнала, т.е. она характеризует скорость распространения группы волн.

Скорость распространения энергии с ростом частоты увеличивается, в области высоких частот она практически не зависит от частоты, , где С – скорость света в свободном пространстве, эта скорость всегда меньше скорости света. Для ТЕМ - волн фазовая скорость не зависит от частоты, определяется

. (4.23)

Для волн Е(ТМ) и Н(ТМ) фазовая скорость зависит от частоты и определяется

,

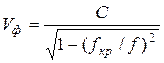где - критическая частота, при которой прекращается распространение энергии по НС.

Зависимость фазовой скорости от частоты указывает на наличие дисперсии в НС. Это обозначает, что различные типы волн в НС распространяются с различными скоростями. В двухпроводных линиях дисперсия отсутствует, дисперсия проявляется в волноводах и световодах.

Вопросы для самоконтроля

1.     Объясните сущность поверхностного эффекта.

2.     Объясните, какие физические процессы происходят в диэлектриках.

3.     Объясните сущность эффекта близости и эффекта действия окружающих масс.

4.     Что такое глубина проникновения?

5.     В каких проводных НС можно пренебречь эффектом близости?

6.     В каких НС нет эффекта действия окружающих масс?

7.     Назовите первичные параметры передачи, объясните их смысл.

8.     Назовите вторичные параметры передачи.

9.     Поясните эквивалентную схему двухпроводной цепи.

10.           Поясните смысл выражения 4.12.

11.           Поясните смысл уравнений 4.16.

12.           Дайте определение волнового сопротивления, объясните его смысл.

13.           Какая линия называется однородной и согласованной?

14.           Дайте определение коэффициента распространения. Поясните смысл действительной и мнимой его частей.

15.           Объясните необходимость перехода к логарифмическим единицам при определении затухания.

16.           Какие скорости существуют в НС, объясните их смысл.

Письменные задания

1.     Приведите графики зависимостей глубины проникновения для медных и стальных проводников от частоты.

2.     Как изменится глубина проникновения поля в металле при увеличении частоты в М раз?

3.     Проводники имеют одинаковую проводимость и ; ; . Сравните глубину проникновения в каждом из этих проводников на частоте f.

4.     Запишите выражение для полного активного сопротивления витой пары, ленточного кабеля, воздушной линии связи.

5.     Приведите зависимость волнового сопротивления от частоты.

6.     Из 4.18 получите аналитические выражения для затухания и коэффициента фазы.

7.     Приведите характер изменения тока вдоль линии.

8.     Приведите частотную зависимость скорости распространения электромагнитной энергии.

9.     Приведите частотную зависимость фазовой скорости от частоты для Т- волны и для Е, Н – волны.

10.           Определите километрическое затухание линии длиной 10 км., если мощность сигнала в начале линии Вт, а в конце линии мВт.

11.           Определите километрическое затухание линии длиной 5 км, если дБ, а мВт.

12.           При измерении волновых сопротивлений симметричной цепи на частоте 0.5 кГц, 20 кГц, 200 кГц получили следующие значения Ом, Ом, Ом. Какой частоте соответствуют измеренные волновые сопротивления?

5. Теория направляющих систем

5.1. Передача энергии по симметричной цепи с учётом потерь

При передаче энергии по НС потери в проводнике определяются радиальной составляющей вектора Пойтинга, которую формирует составляющие и . Мощность потока энергия для цилиндрического проводника определяется

,

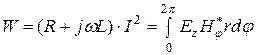откуда 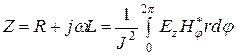, (5.1)

где L – внутренняя индуктивность проводника, а R - его активное сопротивление.

Анализируем гармонические колебания в квазистационарном режиме, среда не содержит сторонних токов, токи смещения отсутствуют, т.е. .

Для определения составляющих поля необходимо воспользоваться уравнениями Максвелла:

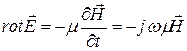; (5.2)

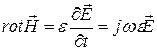. (5.3)

Применим операцию к (4.2):

. (5.4)

Для любого вектора выполняется тождество

, (5.5)

где - оператор Лапласа.

Решение уравнений Максвелла для цилиндрического проводника целесообразно проводить в цилиндрической системе координат. Тогда

.

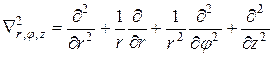Учитывая отсутствие в системе сторонних токов, а следовательно и свободных зарядов, и .

Тогда (5.4) с учётом (5.3) примет вид:

. (5.6)

Полученное уравнение называется волновым. Обычно волновое уравнение решается для продольных составляющих поля и , которые дают возможность определить все шесть составляющих электромагнитного поля.

Распределение продольных составляющих поля вдоль линии представляется как . Тогда волновое уравнение примет вид

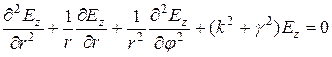, (5.7)

где - поперечное волновое число, для Т – волн , т.е. , т.к. анализируется процесс распространения в металле, обозначим - волновое число для металла. Уравнение (5.7) – это уравнение частных в производных с разделяющимися переменными, его решение для металла имеет вид:

, (5.8)

Это выражение описывает структуру поля в поперечном сечении системы. Первый сомножитель определяет распределение поля в радиальном направлении, второй в азимутальном.

где A, B, C, D – постоянные интегрирования, - коэффициент вихревых токов для металла, и - модифицированные функции Бесселя n–го порядка второго рода. Постоянные интегрирования определяются из граничных условий на границе раздела сред металл / диэлектрик.

Так как поле внутри проводника возрастает от центра к периферии, а функция с увеличением аргумента уменьшается, необходимо принять . В силу симметричного расположения проводников относительно горизонтальной оси, нечётная функция должна обращаться в нуль, т.е. . Учитывая наличие бесконечного числа составляющих поля, получим для проводников

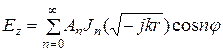. (5.9)

Составляющую магнитного поля определим как

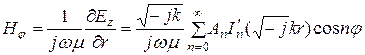. (5.10)

определяются из граничных условий и закона полного тока. Функции Бесселя второго рода это функции комплексной переменной, представляются в виде суммы действительной и мнимой составляющих.

(5.11)

и аргумент этих функции имеет вид

т. к. .

Таким образом, полученные выражения и после подстановки их в (6.1) и разделения этого выражения на действительную и мнимую части позволяют получить аналитические выражения для R и L:

. (5.12)

где I – ток в цепи.

Далее необходимо в (6.12) подставить (6.9) и (6.10) и (6.11), произвести соответствующие преобразования.

Дальнейшие преобразования являются достаточно громадно, окончательные выражения для активного сопротивления и внутренней индуктивности принимают вид

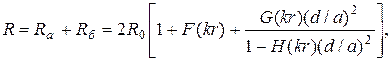(5.13)

, (5.14)

Внутренняя индуктивность симметричной цепи определяется выражением, Гн/км

где d – диаметр проводника, а – расстояние между ними (рис. 5.1), - сопротивление проводника по постоянному току. Функции I, F, H, G, Q определяются комбинациями функций Бесселя, их значения приведены в таблицах (см. приложение), , r– радиус проводника.

С учётом различных скруток в кабеле выражение для расчёта сопротивления симметричного кабеля имеет вид, Ом/км

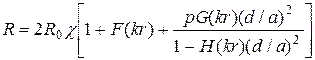. (5.15)

При парной скрутке , при звёздной – , при двойной парной - ; в зависимости от диаметра кабеля. На рис. 5.1 приведено распределение магнитного поля симметричной пары. Поля проводников а и б взаимодействуя между собой увеличивают сопротивление цепи.

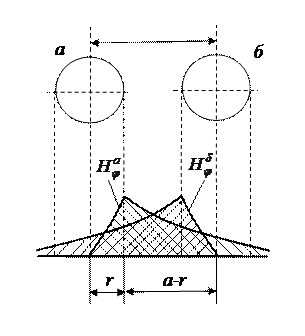
Рис. 5.1. Поле симметричной пары

Первое слагаемое в (5.15) определяет сопротивление цепи по постоянному току, второе – сопротивление вследствие поверхностного эффекта, а третье – сопротивление вследствие эффекта близости.

5.2. Внутренняя индуктивность, емкость и сопротивление изоляции симметричной цепи

В двухпроводной цепи распространяется ТЕМ-волна, т.е. структура поля в поперечном сечении эквивалентна структуре поля постоянного тока и постоянных зарядов, поэтому для определения внешней индуктивности и ёмкости можно воспользоваться известными соотношениями для статического режима (определение ёмкости С) и стационарного (определение индуктивности L) режима. Индуктивность определяет способность системы накапливать магнитную энергию.

Внешняя индуктивность определяется на длину линии в 1 км, используя соотношения

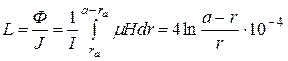, Гн/км , (5.17)

где Ф – магнитный поток, I – ток в системе.

Внешняя индуктивность не зависит от частоты, она определяется геометрией системы.

Общая индуктивность симметричной кабельной цепи,

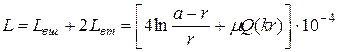. (5.18)

Ёмкость Си проводимость изоляции G связаны с процессами в диэлектрике. Под действием переменного электромагнитного поля в диэлектрике происходит переориентация диполей и поляризация диэлектрика. Ёмкость характеризует возможность системы проводников запасать энергию электрического поля, поляризацию диполей, величину токов смещения. Проводимость изоляции определяет величину потерь в диэлектрике на поляризацию диполей и характеризуется тангенсом угла диэлектрических потерь . Ёмкость определяется соотношением

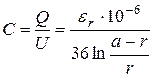, Ф/км, (4.19)

где Q – заряд в системе, U – разность потенциалов между проводниками. Ёмкость цепи не зависит от частоты.

Для определения проводимости изоляции воспользуемся частью схемы двухпроводной цепи, содержащей поперечные параметры (рис. 4.2).

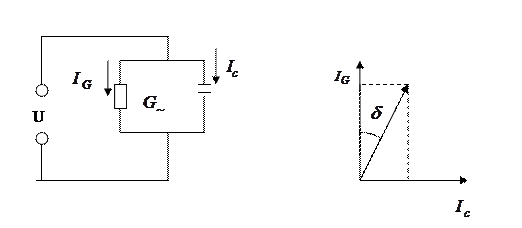
а) б)

Рис. 5.2 – Схема цепи с поперечными параметрами (а) и векторная диаграмма для этой цепи (б)

; ; ,

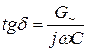откуда получаем

В общем случае, сопротивление изоляции содержит две составляющих

,

где – сопротивление изоляции постоянному току, т.е. . Обычно , поэтому .

Кабели связи, как правило, имеют сложную комбинированную изоляцию, в расчетах принимаются эквивалентные значения и , учитывающие долю диэлектрика в общем объёме изоляции. Следует отметить, что с ростом частоты увеличивается, но в диапазоне частот, в котором используется та или иная цель это величина практически постоянная.

5.3. Вторичные параметры передачи симметричных цепей

Вторичные параметры передачи следует рассчитывать по формулам (3.11, 3.14, 3.15, 3.16). Вторичные параметры с некоторыми допущениями можно выразить непосредственно через геометрические параметры цепей и параметры изоляционных материалов . Волновое сопротивление определяется

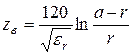, . (5.20)

Затухание рассчитывается по формуле:

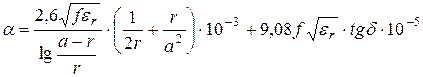, . (5.21)

Коэффициент фазы и скорость распространения определяются

или , ;

, ,

где – скорость света в свободном пространстве, .

Для симметричных цепей, в которых (воздушные линии связи, ленточные кабели), волновое сопротивление и затухание рассчитывается по формулам:

;

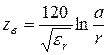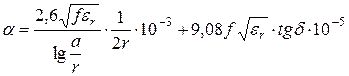. (5.22)

Первое слагаемое в (5.21) и (5.22) определяет потери в металлах, а второе – потери в диэлектрике. Потери в диэлектрике значительно меньше, чем потери в металле. С ростом частоты оба вида потерь возрастают – потери в металле пропорционально , а в диэлектрике – пропорционально частоте.

Вопросы для самоконтроля

1.            Объясните методику определения сопротивления и внутренней индуктивности проводника.

2.            Какие слагаемые в 5.13 определяют сопротивление постоянному току; сопротивление, вызванное поверхностным эффектом; сопротивление, вызванное эффектом действия окружающих масс?

3.            Дайте определение внутренней и внешней индуктивности цепи.

4.            Какие процессы происходят в диэлектрике НС?

5.            Поясните векторную диаграмму на рис 5.2 б.

Письменные задания

1.           Приведите зависимость первичных параметров передачи от частоты.

2.           Изобразите поля симметричной цепи, воздушной линии связи, ленточного кабеля (2 проводника). Поясните, как распределение полей влияет на параметры и .

3.           Получите расчётные соотношения для внешней индуктивности и ёмкости симметричной цепи.

4.           Рассчитать сопротивление ленточного кабеля с медными проводниками, если диаметр проводников мм, а расстояние между ними мм на частоте 300 кГц.

5.           Рассчитать первичные параметры передачи симметричной витой пары, если диаметр проводников мм, изоляция сплошная полиэтиленовая, толщина изоляции мм, частота кГц.

6.           По результатам задачи 5 рассчитать вторичные параметры передачи.

7.           Привести графики зависимостей вторичных параметров передачи симметричной цепи от частоты.

8.           Пользуясь (3.11) определить пределы изменения в зависимости от частоты, сделать вывод.

5.4. Коаксиальные цепи. Электрические процессы в коаксиальных цепях

Основой коаксиального кабеля является коаксиальная пара. Коаксиальная пара - закрытая система, распространение поля в этой НС в радиальном направлении ограниченно и полностью сосредоточено в пространстве между проводниками (рис 4.3).

Рисунок 5.3. Магнитное поле коаксиальной цепи

Особенности распространения электромагнитной энергии по коаксиальной цепи обуславливают возможность передачи широкого спектра частот. Взаимодействие электромагнитных полей внешнего и внутреннего проводников коаксиальной пары таково, что поле за пределами проводника практически отсутствует.

Токи в проводниках и равны по величине, но противоположны по направлению. Следовательно, результирующее магнитное поле вне коаксиальной пары равно нулю:

.

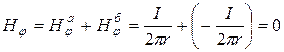Действие поверхностного эффекта и эффекта самоэкранирования в коаксиальной цепи приводит к эффекту самоэкранирования, который иллюстрируется рис. 5.4.

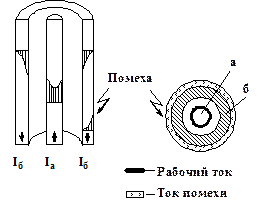
Рисунок 5.4. Эффект самоэкранирования в коаксиальной паре

Сущность эффекта самоэкранирования состоит в том, что рабочие токи сосредоточены на внутренней поверхности наружного проводника, т.е. коаксиальная цепь не создаёт помех соседним цепям. Токи помех, индуцированные внешними помехами, сосредоточены на внешней стороне внешнего проводника, т.е. они не индуцируют поле внутри коаксиальной пары. Эффект самоэкранирования объясняет незначительные взаимные влияния в коаксиальных цепях. С ростом частоты эффект самоэкранирования возрастает, а взаимные влияния уменьшаются, поэтому коаксиальные кабели используются на высоких частотах.

Разновидностью коаксиальных кабелей являются радиочастотные кабели, которые широко применяются в локальных сетях. Эффект самоэкранирования позволяет выполнять внешний проводник в виде оплетки, а не сплошным. Эти кабели используются на частотах до МГц, они обладают высокой помехозащищенностью, однако на высоких частотах имеют большое затухание.

В коаксиальной цепи распространяется ТЕМ–волна. Электрическое поле имеет составляющие и . Радиальная составляющая обуславливает наличие тока смещения в диэлектрике , продольная составляющая тока проводника. Кроме этих составляющих существует тангенциальная составляющая магнитного поля , которую порождает протекающий вдоль проводников ток проводимости .

5.5. Параметры передачи коаксиальных цепей

Методика определения первичных параметров передачи коаксиальной цепи такая же как и для симметричных цепей. Для частот свыше кГц (что практически всегда выполнимо для КК) используются следующие расчётные формулы. Сопротивление цепи для медных проводников определяется

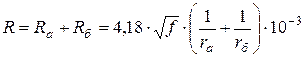, , (5.23)

где – диаметр внутреннего проводника, – внутренний диаметр внешнего проводника, мм., f – частота, Гц.

Внутренняя индуктивность для медных проводников:

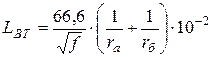, . (5.24)

Внешняя индуктивность определяется поперечными размерами цепи и для медных проводников рассчитывается по формуле

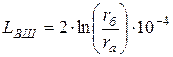, . (5.25)

Следует отметить, что .

Для алюминиевых проводников (4.23) и (4.24) имеют вид:

;

.

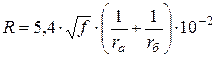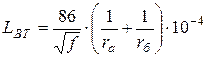Емкость цепи определяется

, .

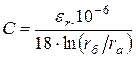Проводимость изоляции равна , См/км. В коаксиальных цепях . Вторичные параметры передачи рассчитываются по формулам:

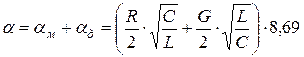дБ/км

; ; ,

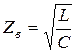где – затухание вследствие потерь в металле, – затухания вследствие потерь в диэлектрике.

Однако вторичные параметры передачи коаксиальных кабелей целесообразно выражать непосредственно через поперечные размеры коаксиальной пары ( и ) и параметры изоляции ( и ). Коэффициент затухания кабелей с медными проводниками определяется, дБ/км

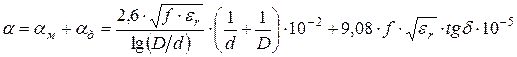. (5.26)

В некоторых типах коаксиальных кабелей внешний проводник часто выполняется из алюминия, при этом затухание кабеля возрастает незначительно. Это подвесные коаксиальные кабели, кабели для распределительных сетей кабельного телевидения. В радиочастотных кабелях наружный проводник часто выполняется из алюминиевой проволочной оплётки.

Как следует из (5.26) потери в металле пропорциональны , а потери в диэлектрике пропорциональны и растут значительно быстрее, чем потери в металле в области высоких частот.

Коэффициент фазы определяется формулой

или , рад/км.

Скорость распространения электромагнитной энергии , для коаксиальной пары

, .

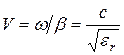Коэффициент фазы линейно возрастает с увеличением частоты. Это обуславливает постоянство скорости распространения энергии по коаксиальному кабелю в широком спектре частот. Такое постоянство необходимо при передачи цифровых сигналов. Скорость передачи уменьшается с увеличением диэлектрической проницаемости. В коаксиальных кабелях скорость передачи электромагнитной энергии приближается к скорости света в свободном пространстве.

Волновое сопротивление ( ) коаксиальной пары для высоких частот определяется выражением:

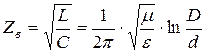(5.27)

или ,

где – волновое сопротивление диэлектрика.

Учитывая, что и , где Гн/м, Ф/м, получим

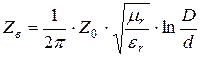, (5.28)

где Ом – волновое сопротивление свободного пространства. Для среды с получим

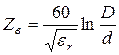. (5.29)

5.6. Оптимальное соотношение диаметров проводников коаксиальной цепи

Оптимальная конструкция коаксиальной пары предполагает при минимальных затратах материалов получить минимально возможные потери энергии.

Анализируя выражения для определения потерь в металле на высоких частотах (5.26), можно сделать вывод, что при определённом соотношении диаметров проводников коаксиальной пары, коэффициент затухания принимает минимальное значение.

Выразив через х продифференцировав первое слагаемое (5.26) по и приравняв производную , получим условие минимума функции

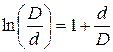(5.30)

Таким образом, минимальное затухание коаксиальной цепи обеспечится отношением . Это соотношение справедливо для кабелей с одинаковыми (медными) проводниками. Характер изменения затухания от соотношения диаметров проводников приведён на рис. 5.5.

Рисунок 5.5. Характер изменения затухания коаксиальной цепи с медными проводниками в зависимости от соотношения диаметров проводников

Так как волновое сопротивление коаксиального кабеля строго нормировано, на практике отношение несколько отличается от оптимального. Волновое сопротивление коаксиальной цепи существенно зависит от величины диэлектрической проницаемости. Для достижения нормированной величины Ом, при необходима изоляция с малым содержанием диэлектрика . При увеличении конструкция коаксиальной пары не является оптимальной, так при .

Если по кабелю необходимо обеспечить передачу большой мощности, то . Если же по кабелю необходимо передать максимальное напряжение, обеспечить максимальную электрическую прочность, то .

Для кабелей связи необходимо обеспечить минимальные потери энергии . Условие передачи максимальной мощности или достижение максимальной электрической прочности необходимо – в фидерах электро питании.

Вопросы и задания для самоконтроля

1.           Какие особенности распространения энергии в коаксиальной цепи?

2.           Какие составляющие поля существуют в коаксиальной цепи?

3.           Объясните сущность эффекта самоэкранирования в коаксиальной цепи.

4.           Как используется эффект самоэкранирования в коаксиальных кабелях различного назначения?

5.           Объясните связь между составляющими поля и токами в коаксиальной цепи.

6.           Объясните, почему коаксиальные кабели используются в области высоких частот.

7.           Какими процессами определяется затухания в металле и затухание в диэлектрике?

8.           Объясните смысл коэффициента фазы.

9.           Как постоянная фазы и скорость распространения влияют на распространение цифровых сигналов?

10.      Чем определяется волновое сопротивление КЦ на высоких частотах?

11.      Каким конструктивным параметром определяется затухание коаксиального кабеля?

12.      Какими параметрами диэлектрика определяется волновое сопротивление КК?

13.      Какие свойства КП определяют различные соотношения её диаметров?

Письменные задания

1.           Приведите структуру электромагнитного поля коаксиальной пары.

2.           Приведите графики зависимостей первичных и вторичных параметров передачи от частоты.

3.           Определите параметры передачи кабеля на частоте МГц, если , проводники алюминиевые, изоляция полиэтиленовая шайбовая.

4.           Рассчитать зависимость затухания КК в зависимости от соотношения диаметров на частоте МГц, изоляция полиэтиленовая пористая мм. Интервал изменения D/d принять от 3 до 4,2 с шагом 0,2.

5.           Коаксиальный кабель для локальной вычислительной сети имеет волновое сопротивление Ом. Определить соотношение диаметров проводников для различных значений диэлектрической проницаемости. Приделы изменения от до , с шагом . При каком значении затухание будет минимальным, максимальным. Определить эти затухания, если тактовая частота в сети МГц, мм.

6.           Какое минимальное затухание может быть получено в кабеле для локальной сети со сплошной полиэтиленовой изоляцией на частоте МГц, если мм? Определить волновое сопротивление этого кабеля.

7.           В какой из коаксиальных пар будет больше затухание: с или ? Объяснить ответ.

5.7. Свойства неоднородных линий

Проведённый выше анализ процессов и явлений в симметричных и коаксиальных цепях предполагал однородность линии. Однородная линия имеет постоянные электрические характеристики на всём протяжении, она нагружена на концах сопротивлениями, равными волновому . В этом случае отраженных электромагнитных волн нет и вся передаваемая энергия полностью поглощается приёмником, электрические процессы в линии точно описываются уравнениями (3.1, 3.2), а затухание линии определяется её собственным затуханием.

При изготовлении кабелей вследствие не совершенства технологии возникают различные дефекты: деформации изоляции, проводников, отклонения диаметров проводников и толщины изоляции от номинальных значений, эллиптичность проводников в коаксиальной паре, их несоосность и др. Вследствие этого кабель становится неоднородным по длине, изменяются его параметры, линия становится неоднородной. Однородность линии определяется постоянством волнового сопротивления по длине линии. Мерой неоднородности линии является коэффициент отражения p в месте сосредоточенной неоднородности (рис. 5.6).

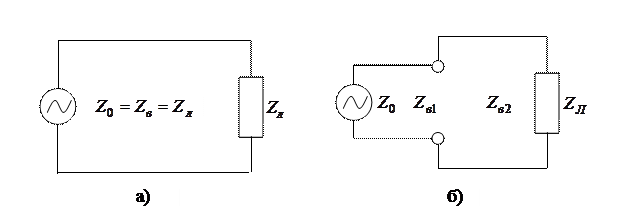
Рисунок 5.6. Схема однородной (а) и неоднородной (б) линии

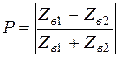. (5.31)

В неоднородной линии появляются отраженные волны, которые искажают характеристику собственного волнового сопротивления линии. Теперь линия характеризуется входным сопротивлением, характер которого приведен на рис. 5.7.

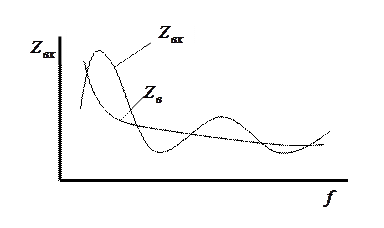
Рисунок 5.7. Частотная зависимость входного сопротивления цепи

Изменение входного сопротивления цепи на её концах приводит к несогласованности на концах линии и к появлению концевых отражений с коэффициентом отражения

,

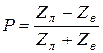где - входное сопротивление линии.

Дальность связи по неоднородной линии будет определяться не собственным затуханием линии , а рабочем затуханием

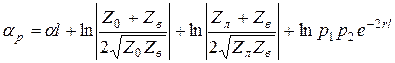, (5.32)

где и – коэффициенты отражения на стыках “генератор–кабель” и “приёмник–кабель”.

; .

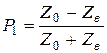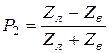Рабочее затухание - более общий параметр, т.к. кроме собственного затухания кабеля , учитывает также влияние несогласованности на стыках кабеля с нагрузкой.

В линиях неоднородных по длине различают внутренние неоднородности - в пределах строительной длины кабеля, и стыковые – обусловленные разбросом конструктивных, а следовательно, и электрических параметров.

Стыковые неоднородности, как правило, превышает внутренние неоднородности в кабеле сказываются, главным образом, на волновом сопротивлении кабеля, величина которого в месте сосредоточенной неоднородности отличается от номинальной.

Реальный кабель является неоднородной цепью. Электромагнитная волна, распространяясь по такой цепи и встречая на своём пути неоднородность, частично отражается от неё и возвращается к началу линии. При наличии нескольких неоднородных участков при распространении волны возникают многократные частичные отражения, что вызывает увеличение рабочего затухания и искажения характеристик цепи.

Неоднородности в кабеле приводят к появлению в цепи двух дополнительных потоков энергии: обратного (встречного), движущегося к началу цепи (генератору), и попутного, совпадающего с основным потоком. Схема образования встречных и попутных потоков представлена на рис. 5.2.

Рисунок 5.8. Схема образования встречного и попутного потоков

Попутный поток особенно проявляется на длинных линиях. Попутный поток искажает форму передаваемого сигнала, создаёт помехи. Появление попутного потока отрицательно влияет на передачу телевизионных сигналов, т. к. в этом случае нарушаются фазовые соотношение в структуре ТВ сигнала.

Величина попутного потока не должна превышать 1% основного. В аналоговых системах передачи попутный лимитируется на участке ОП1 – ОП2 линии, а в цифровых – на длине регенерационного участка.

Для повышения однородности электрических характеристик линии производится группирование строительных длин кабеля. При этом строительные длины располагают так, чтобы величины их волновых сопротивлений нарастали от начала регенерационного (усилительного) участка к его середине. На концах линии прокладываются кабели с номинальным волновым сопротивлением.

Вопросы для самоконтроля

1.     Дайте определение однородной и неоднородной линии.

2.     Чем характеризуется степень однородности линии?

3.     Какие факторы приводят к неоднородности линии?

4.     Дайте определение рабочего затухания.

5.     Объясните смысл всех слагаемых в 5.1.

6.     Как образуются встречный и попутный потоки?

7.     Как влияют встречный и попутный потоки на передачу различных сигналов?

8.     Какие неоднородности существуют в кабелях?

9.     Какие меры применяются для повышения однородности линии?

Письменные задания

1.     Определить рабочее затухание линии длиной 10 км, если затухание кабеля составляет 2 дБ/км, если волновое сопротивление кабеля Ом, Ом, Ом.

2.     Мощность генератора в начале линии Вт, длина линии км, её километрическое затухание составляет дБ/км. Определить мощность обратного потока в начале линии, если Ом, а Ом.

3.     Определить допустимое отклонение волнового сопротивления от номинального ( Ом), чтобы коэффициент отражения не превышал 0.02.

4.     Предложить вариант группирования строительных длин кабеля с волновыми сопротивлениями: Ом, Ом, Ом, Ом, Ом.

6. Волноводы

Волновод – закрытая направляющая система, в которой распространение энергии ограничивается в поперечном направлении. Это однопроводная система, следовательно в ней могут распространяться поперечные электрические (TE,H) и поперечные магнитные (TH,E) волны, а поперечные электромагнитные волны распространяться не могут. В волноводах преобладают токи смещения, токи проводимости незначительны, они протекают по проводящим стенкам волновода и замыкаются токами смещения вследствие непрерывности линий тока. Наиболее распространенными являются прямоугольные и круглые волноводы. Особенность волновода, как направляющей системы, состоит в том, что в нем могут распространяться волны с длиной волны не превышающей критическую. Аналз проводится для гармонических колебаний, множитель опущен.

Для анализа свойств волновода рассмотрим сначала особенности распространения волн между двумя бесконечными проводящими плоскостями (рис. 6.1). Используя уравнения Максвелла получим волновое уравнение для этой структуры.

Рис. 6.1. Бесконечные проводящие плоскости.

Рассмотрим поперечно-магнитное поле для системы (рис. 6.1). Волновое уравнение относительно составляющей запишется в виде:

(6.1)

где 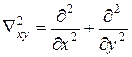- оператор Лапласа в прямоугольной системе координат; - волновое число, тогда (6.1) примет вид

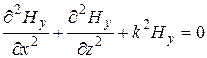. (6.2)

В соответствии с рисунком В.1 предположим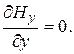

Уравнение (6.2) – дифференциальное уравнение 2-го порядка с разделяющимися переменными, которое после соответствующих преобразований представляется в виде системы двух дифференциальных уравнений:

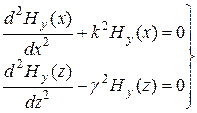, (6.3)

где - постоянная распространения, а - поперечное волновое число.

Решение системы (6.3) представляется в виде:

. (6.4)

Первый сомножитель в (6.4) определяет структуру поля в поперечном сечении системы, а второй – описывает распространение волны вдоль оси z. Учитывая, что при волна затухает, полагаем D=0.

Чтобы найти постоянные интегрирования в (6.4), необходимо воспользоваться граничными условиями для составляющих поля. Известно, что касательные составляющие электрического поля на проводящих поверхностях обращаются в нуль, т.е.

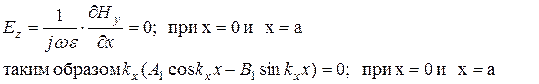(6.5)

Условие (6.5) выполнимо при . В этом случае не только на проводящих плоскостях, но и в пространстве между ними, т.е. .

Это решение уравнений (6.3) является не единственно возможным. Условиям (6.5) можно удовлетворить и при , т.е. необходимо выполнение равенства:

, при х=0 и х=а. (6.6)

Левая часть (6.6) обращается в нуль при х=0 и х=а, если

и ,

откуда вытекает , где m=0,1,2… (6.7)

Таким образом получим:

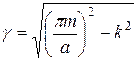, m=0,1,2… (6.8)

Легко заметить, что при постоянная распространения становится мнимой величиной, поперечно-магнитное поле в этом случае будет иметь волновой характер. Так как m – любое целое число, то в пространстве между параллельными проводящими плоскостями может существовать бесчисленное множество типов волн (мод), характеризующихся различными значениями m и различной структурой поля.

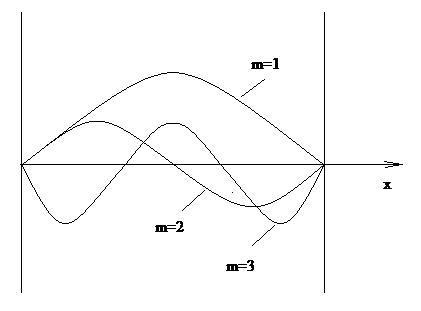
Рис. 6.2. Волны между параллельными плоскостями.

В анализируемой системе могут распространяться только волны, удовлетворяющие условию:

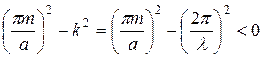, (6.9)

откуда при m=1 получаем .

Таким образом, система является фильтром верхних частот, в системе существует частота отсечки, или критическая частота, удовлетворяющая (6.8).

Приведенный анализ позволяет сделать важнейшие выводы:

• возможность распространения волн между двумя параллельными плоскостями определяется расстоянием между этими плоскостями;
• в пространстве между проводящими плоскостями могут распространяться поперечно-электрические и поперечно-магнитные волны;
• множество распространяющихся в системе волн (мод) является дискретным;
• распространение Н- и Е-волн начинается с определенной частоты, называемой критической, Н- и Е-волны с частотой ниже критической не распространяются;
• критическая частота (длина волны) определяется расстоянием между проводящими плоскостями.

При распространении энергии между проводящими плоскостями можно выделить 3 режима (рис. 6.3): распространение, близкое к прямолинейному, режим многократных отражений, критический режим.

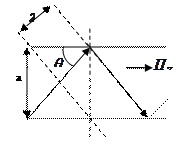
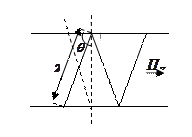
а) б) в)

Рис. 6.3 – Распространение электромагнитной волны: а) близкое к прямолинейному; б) режим многократных отражений; в) критический режим (стоячая волна)

Приведенный анализ справедлив для изучения процессов в волноводах и световодах, в любых системах, в которых распространяются поперечные волны.

Проще всего приведенный анализ распространить на прямоугольный волновод (рис. 6.4). Анализ проводится для гармонического колебания.

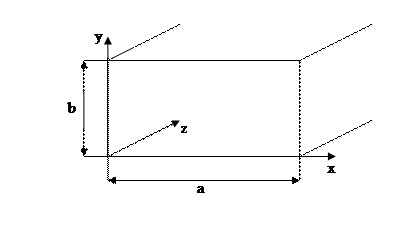
Рис. 6.4. Прямоугольный волновод

Рассмотрим Н-волны. Как и для системы из параллельных плоскостей, при анализе процессов в волноводе из уравнений Максвелла получаем волновое уравнение относительно составляющей :

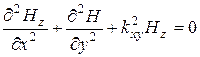, (6.10)

где - поперечное волновое число, согласно (6.7) .

Зависимость представляется в виде:

,

где .

Дифференциальное уравнение (6.10) сводится к системе двух уравнений:

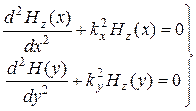. (6.11)

Решение этих уравнений представляется в виде:

;

; (6.12)

.

Учитывая граничные условия для составляющих электрического поля: при y=0, y=b и при x=а и х=0 и связь между и поперечными составляющими имеет вид:

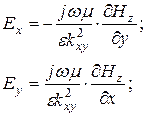(6.13)

получим составляющую поля :

; (6.14)

где .

Учитывая (6.13) можно получить и другие составляющие поля. При m=n=0 все составляющие поля, кроме , обращаются в 0, следовательно, m и n могут принимать любые значения, равные 0, 1, 2…, но они не должны одновременно равняться нулю. Аналогичные рассуждения можно привести и для Е-волн.

Таким образом, в прямоугольном волноводе существует бесчисленное множество поперечно-электрических, или Н-волн, и поперечно-магнитных, или Е-волн, которые характеризуются разными значениями m и n. Вдоль сторон a и b распределение поля имеет форму стоячей волны, причем m определяет число полуволн (вариаций поля), укладывающихся на интервале , а n – число полуволн на интервале . Поле будет распространяться по оси z в виде бегущей волны, если - мнимая величина:

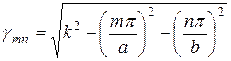. (6.15)

Для того, чтобы волна распространялась вдоль оси z необходимо выполнение условия

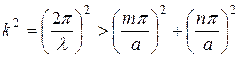. (6.16)

Таким образом, в волноводе, как и в системе из двух параллельных плоскостей, может распространяться дискретный набор типов волн (мод), условие их распространения определяется (6.16), этим же соотношением определяется длина волны распространяющихся колебаний. В отличие от системы двух параллельных плоскостей длина волны ограничивается уже двумя параметрами a и b. В волноводе невозможно распространение ТЕМ-волны. После преобразований (6.16) получим выражение для критической частоты волны. Волны, частоты которых меньше , в волноводе не распространяются.

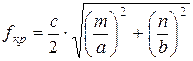, m=0, 1, 2… (6.17)

.

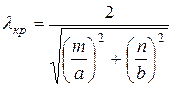Возможность распространения волн в прямоугольном волноводе определяется его поперечными размерами. Волна, имеющая простейшую структуру поля и наибольшую длину, называется основной, такой волной в прямоугольном волноводе является волна . Низшие типы волн имеют затухание меньшее, чем высшие типы. Возбуждение в волноводах высших типов волн приводит к увеличению потерь, эти волны возбуждаются при наличии неоднородностей. В волноводе основными являются токи смещения, токи проводимости, протекающие по стенкам волноводов незначительны, т.е. . Токи проводимости в волноводах являются поверхностными, они протекают по очень тонкому поверхностному слою его стенок (вследствие поверхностного эффекта). Для уменьшения потерь в волноводе его спинки изготавливаются с высокой степенью чистоты и покрываются тонким слоем металла с высокой проводимостью, как правило серебром.

6.1. Круглый волновод

В круглом волноводе электромагнитное поле представляется в виде совокупности поперечно – электрических (Н – волны) и поперечно – магнитных (Е - волны) различных типов.

Так же и в теории прямоугольных волноводов, из уравнений Максвелла можно получить волновое уравнение для или составляющих. Рассмотрим Н – волны, для которых волновое уравнение имеет вид

, (6.18)

где - поперечное волновое число, - оператор Лапласа в цилиндрической системе координат, тогда (6.18) запишется:

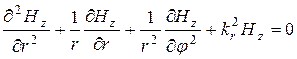(6.19)

Как и в предыдущем анализе рассматриваем гармонические колебания, волна распространяется вдоль оси Z, т. е. .

Решение волнового уравнения в цилиндрической системе координат представляется совокупностью функций Бесселя и гармонических функций.

(6.20)

Функции Бесселя второго рода при обращаются в бесконечность. Из физических условий ясно, что поле в центре волновода ( ) должно иметь конечное значение, т. е. . Тогда (В.20) будет иметь вид:

. (6.21)

Так как функция не должна изменяться при замене на , то может быть лишь целым числом, т. е. Для рассматриваемой системы должно выполняться граничное условие , при , это условие выполнимо 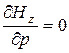при

при , или ,

Таким образом, делаем вывод, что граничное условие выполнимо при обращении производных соответствующих производных функций Бесселя в нуль, т. е. аргумент функции является корнем производной функции Бесселя первого рода порядка , обозначим этот корень . Учитывая соотношение , определяем критическую частоту в круглом волноводе

. (6.22)

Индекс m определяет порядок функции Бесселя, а n – номер её корня. В структуре поля m определяет число полуволн вдоль диаметра волновода, а n – вдоль его окружности, т. е. число вариаций по диаметру и по азимуту.

Аналогичный анализ можно провести и для Е – волн, в этом случае условие распространения поля определяется

при , ,

где - n – ый корень функции Бесселя m – го порядка. Как видно из анализа, в круглом волноводе также распространяется бесчисленное множество (континуум) мод, условие распространения которых определяется обращением в нуль функций Бесселя (Е - волны) или их производных (Н - волны), а значения критических частот определяются значениями корней этих функций.

В круглом волноводе основной является волна , при радиусе волновода а она имеет наибольшую критическую длину волны . В этом смысле волна является аналогом волны в прямоугольном волноводе. В таблице 6.1 приведены структуры поля некоторых типов волн и их критические частоты.

Таблица В1

Характеристика	Тип волны
Поле в плоскости поперечного сечения
Компоненты полей, отличные от нуля	, , , ,	, ,	, ,

Особый интерес представляет в круглом волноводе волна . Затухание этой волны с ростом частоты, в отличие от других волн, уменьшается (рис. 6.5).

Это объясняется следующим образом. Все типы волн, кроме , имеют электрическое поле, линии которого замыкаются на стенках волновода, т.е. возникают токи проводимости на стенках, приводящие к тепловым потерям и увеличению затухания, с ростом частоты эти потери возрастают. Силовые линии электрического поля волны циркулируют по поперечным замкнутым окружностям (табл. 6.1) внутри волновода и не соприкасаются со стенками волновода. Этим линиям соответствуют токи смещения в диэлектрике , в металлических стенках токи отсутствуют. С увеличением частоты силовые линии электрического поля концентрируются в центре волновода.

Однако волна не является основной, кроме того, она является неустойчивой, так как линии поля не имеют жесткой связи со стенками волновода. Эта волна чувствительна к различным неоднородностям и деформациям в волноводе и легко трансформируется в другие высшие типы волн.

Для повышения устойчивости этой волны используются не сплошные волноводы, а спиральные, тогда кольцевые токи смещения поддерживаются спиральными токами в стенках волновода. Спиральные волноводы имеют большее затухание, чем сплошные, поэтому на практике в круглых волноводах используются вставки из спиральных волноводов.

Волноводы непосредственно для организаций линий связи не применяются, т. к. они имеют ряд недостатков. Они применяются в антенно – фидерных трактах в радиорелейной связи, в наземных станциях спутниковых систем связи.

Вопросы для самоконтроля

1.           Какие классы и типы волн (моды) распространяются между двумя проводящими плоскостями?

2.           Объясните смысл уравнения 6.4.

3.           Объясните смысл граничных условий для составляющих поля.

4.           Что такое критическая частота (длина волны)?

5.           Чем определяется в системе из проводящих бесконечных плоскостей?

6.           Охарактеризуйте режим передачи в системе из плоско – параллельных плоскостей?

7.           Объясните смысл уравнений 6.12.

8.           Какие классы и типы волн распространяются в волноводах?

9.           Чем определяется критическая частота (длина волны) в волноводе?

10.      Объясните смысл индексов m и n.

11.      Объясните смысл уравнения 6.20.

12.      Каким условиям удовлетворяет распространение электрических и магнитных волн в круглом волноводе.?

13.      Какой основной тип волны в круглом волноводе?

14.      Объясните особенности волны в круглом волноводе.

15.      Объясните особенности спиральных волноводов.

Письменные задания

1.     Определите критические длины волн , для прямоугольного волновода.

2.     Приведите структуру поля волны в прямоугольном волноводе.

3.     Определите критические длины волн , , если диаметр волновода равен 4 см.

4.     Какой тип волны необходимо возбудить в круглом волноводе, чтобы затухание линии длиной 50 м. при длине волны не превышало дБ.

5.     Охарактеризуйте достоинства и недостатки волноводов.

7. Волоконные световоды

7.1. Полное внутренние отражения

Волоконные световоды используются для передачи информации электромагнитными волнами оптического диапазона. В технике волоконно – оптической связи используется ближний инфракрасный диапазон (рис. 7.1), который занимает определённое место на шкале электромагнитных волн.

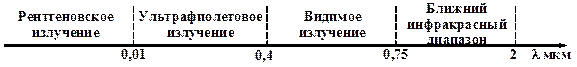
Рис. 7.1. Шкала электромагнитных волн

Волоконные световоды обладают уникальными качествами, отличающими их от направляющих систем с металлическими границами. Основными свойствами ВС являются:

• малые поперечные размеры;
• малый коэффициент затухания, не зависящий от поперечных размеров ВС и частоты модулирующего сигнала;
• высокая скорость передачи информации;
• неподверженность внешним электромагнитным воздействиям;
• отсутствие взаимных влияний;
• гальваническая развязка цепей передачи и приёма;
• отсутствие коротких замыканий.

Волоконные световоды являются основой волоконно – оптических кабелей. Волоконный световод состоит из сердцевины с показателем преломления и оболочки с показателем преломления , причём (рис. 7.2)

Рис. 7.2. Структура волоконных световодов.

Волоконные световоды как среда передачи в технике оптической связи определяют параметры системы и её назначение в целом. Направляющие свойства волоконных световодов, плёночных (планарных) и полосковых оптических волноводов основаны на явлении полного внутреннего отражения света. Такие структуры состоят их оптически прозрачного вещества, окруженного оптически менее плотным материалом. Световые лучи, падающие на торец такой структуры, при определённых условиях захватываются и направляются плёнкой, полоской или волокном. Такое объяснение направляемости света, использующее законы геометрической оптики не учитывает свойства света как электромагнитной волны, поэтому при анализе процессов распространения электромагнитной энергии в световодах используется два подхода – лучевое приближение и волновая теория. Лучевое приближение, основанное на законах геометрической оптики, просто, наглядно, дает качественное представление о процессах распространения в световодах, позволяет произвести некоторые количественные оценки. В геометрической оптике световые волны изображаются лучами, направленными по нормали к волновой поверхности. В оптически однородных средах лучи прямолинейны. При падении световой волны на плоскую границу раздела двух сред с разными значениями относительной диэлектрической проницаемости е (или показателя преломления n) в общем случае появляются прошедшая (преломленная) и отраженная волны, при этом предполагается, что обе среды не поглощают свет (рис. 7.3). Углы падения, отражения и преломления связаны соотношением, известным как закон Снеллиуса

(7.1)

где — показатель преломления первой среды, в которой распространяется падающая волна; — показатель преломления смежной среды.

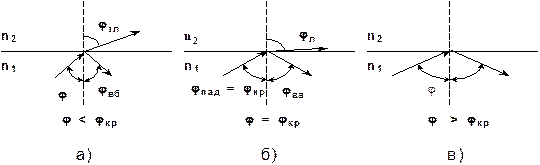
Рис. 7.3. Полное внутреннее отражение

Если световая волна из оптически более плотной среды падает на границу раздела с оптически менее плотной средой ( > ), то угол падения всегда меньше угла преломления ( < ). С увеличением угла падения увеличивается и угол преломления , пока не наступит момент, когда =90°, т.е. преломленный луч в этом случае скользит вдоль границы раздела двух сред. Таким образом всегда существует критический предельный угол падения при котором преломленная волна распространяется вдоль границы раздела сред ( =90°).

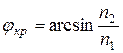, (7.2)

При дальнейшем увеличении угла падения (т.е. при < ) преломленная волна отсутствует и вся энергия, содержащаяся в падающем луче, полностью отражается от поверхности оптически менее плотной среды (рис. 7.2). Это явление называется полным внутренним отражением. Отраженная волна при этом приобретает фазовый сдвиг, зависящий от угла падения.

Лучевая модель распространения света в световодах не позволяет учесть и проанализировать фазовые соотношения между падающими и отраженными волнами, а также энергетические соотношения между ними. Учет волновых свойств света показывает, что из всего множества световых лучей в пределах угла полного внутреннего отражения от границы направляющей структуры только ограниченное число лучей с дискретными углами могут образовать направляемые волны структуры. Кроме полного внутреннего отражения эти лучи должны удовлетворять еще условию, которое заключается в том, что после двух последовательных переотражений от стенок соответствующие лучам волны должны быть в фазе и таким образом интерферировать при наложении друг на друга. Только когда волны удовлетворяют такому фазовому условию, они будут формировать согласованное распределение поля направляемых волн (мод). Если это условие не выполняется, волны интерферируют так, что гасят сами себя и исчезают. Квантование полей в дискретный ряд направляемых мод было обнаружено только тогда, когда были решены уравнения Максвелла.

Наиболее полные результаты процессов распространения и отражения в световодах, а также энергетические соотношения можно получить, только используя волновую теорию. При анализе процессов распространения в световодах основными являются следующие положения:

• свет, излучаемый каким-либо источником и распространяющийся в свободном пространстве, имеет вид однородной плоской волны если источник или какие-либо рассеивающие объекты или границы достаточно удалены от места наблюдения;
• в прозрачной, однородной и достаточно протяженной среде свет также может распространяться в виде однородных плоских волн;
• материалы, из которых изготовлены световоды, являются немагнитными, изотропными и линейными относительно векторов электрического и магнитного полей.

7.2. Числовая апертура и апертурный угол

Световые лучи, падающие на торец при определенных условиях захватываются сердцевиной ВС и распространяются вдоль него (рис 7.4).

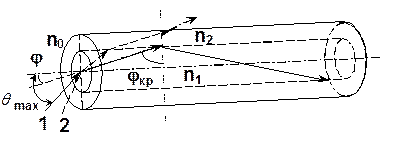
Рис. 7.4. К определению апертурного угла

В сердцевине и оболочке существует два типа лучей: меридиональные, которые расположены в плоскости, проходящей через ось ВС и косые, не пересекающие эту ось. Если точечный источник излучения расположен на оси ВС, то существуют только меридиональные лучи. Если же точечный источник расположен вне оси, или имеется сложный источник, то появляются одновременно как меридиональные, так и косые лучи.

Рассмотрим ход меридиональных лучей, падающих из свободного пространства с показателем преломления на торец ступенчатого ВС и распространяющихся затем вдоль сердцевины (рис. 7.4). Луч, падающий под углом к оси световода, преломляется на торцевой поверхности под углом , а затем падает на границу раздела сердцевина–оболочка под углом , далее в зависимости от величины угла он частично или полностью отражается в сердцевину. В соответствии с (7.1) на границе раздела внешняя среда–торец ВС

. (7.3)

На границе раздела сердцевина–оболочка при < луч распространяется вдоль сердцевины, многократно отражаясь на границе с оболочкой, при этом выполняется условие (7.2).

При = получается максимальный угол падения (ввода), при котором луч удерживается сердцевиной, этот угол называется апертурным углом, обычно он характеризуется величиной , которая называется числовой апертурой.

С учетом (7.2), (7.3) после преобразований найдем значение числовой апертуры

. (7.4)

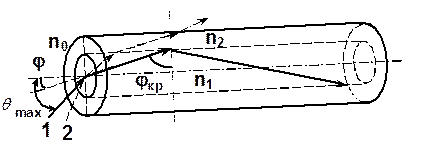
Рис. 7.4. К расчету числовой апертуры

Апертурный угол ступенчатого ВС определяет половину угла при вершине конического пучка лучей, которые захватываются и направляются ВС.

Числовая апертура является важным параметром ВС, она определяется эффективность ввода излучения в ВС, потери на изгибах, дисперсию, число распространяющихся мод. Увеличение разности показателей преломления увеличивает апертурный угол, что увеличивает эффективность ввода излучения в волокно, но при этом увеличивается дисперсия.

Числовая апертура зависит от материала и способа изготовления световодов. В технике связи наибольшее распространение получили световоды на основе кварцевых стекол, получаемые способом осаждения из газовой среды. Для изменения показателя преломления кварцевого стекла (окиси кремния) используют различные добавки, в том числе фосфор, германий, бор, титан, алюминий. Относительная разность показателей преломления в одномодовых кварцевых волокнах изменяется в пределах 0,002—0,01, а в многомодовых ВС от 0,005 до 0,02. Обычно числовая апертура ВС равна 0,18—0,25.

Формула (7.4) учитывает только меридиональные лучи ВС, од­нако в реальных условиях лишь часть пучка световых лучей источника преобразуется в меридиональные лучи, с ВС распространяются также и косые лучи, поэтому вводится понятие действительной числовой апертуры , учитывающей и косые лучи ( ).

В зависимости от числа распространяющихся на рабочей длине волны мод ВС делятся на одномодовые (распространяется одна волна) и многомодовые.

В соответствии с требованиями ITU для многомодовых ВС диаметр сердцевины 2а=50 мкм, диаметр оболочки 2b=125 мкм, диаметр сердцевины одномодовых ВС составляет обычно 8 – 10 мкм.

Для характеристик ВС большое значение имеет закон изменения показателя преломления как функции его радиуса n=n(r), который называется профилем показателя преломления (ППП). Наибольшее распространение получили ВС двух типов: со ступенчатым ППП (ступенчатые) и градиентным ППП (градиентные). В ступенчатых ВС показатель преломления в сердцевине постоянен, и существует резкий переход от сердечника к оболочки, т.е.

.

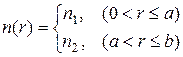Градиентные ВС имеют непрерывное плавное изменение показателя преломления в сердцевине по радиусу световода

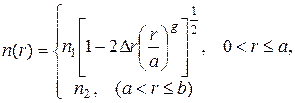
где 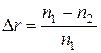– относительная разность показателей преломления, r – текущий радиус.

На рис. 7.5 приведены поперечные сечения и типовые распределения показателей преломления ВС.

Двухслойное волокно с однородными сердцевиной и оболочкой и скачком показателя преломления между ними является идеализированной моделью, от которой реальные волокна несколько отличаются. Даже в том случае, когда исходные материалы сердцевины и оболочки однородны, при нагреве и вытяжке волокна происходит диффузия материала, которая размывает границу между сердцевиной и оболочкой. При изготовлении градиентных световодов по технологическим причинам часто получают в центре сердцевины область с уменьшенным значением показателя преломления (рис. 2.10 д). Такие ВС называются световодами с осевым провалом в ППП.

ВС с g=2 называются параболическими, т.к. профиль показателя преломления описывается параболой. ВС с градиентным ППП обладают лучшими свойствами для передачи сигналов, чем ступенчатые ВС, наилучшим ВС для передачи сигналов является ВС с параболическим ППП. На рис. 7.6 б показан ход лучей в градиентном ВС.

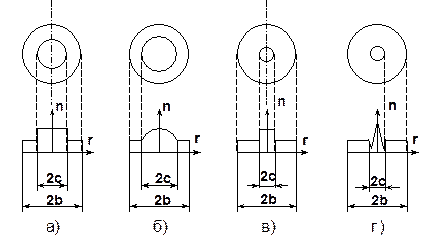
а) многомодовый ВС со ступенчатыми ППП; б) градиентный ВС; в) одномодовый ВС; г) ВС W-типа

Рис. 7.5. Профили показателей преломления ВС

Профиль показателя преломления определяет траекторию распространения лучей в ВС на рис. 7.6 приведены примеры хода лучей в разных типах ВС.

Рис. 7.6. Распространение света в разных типах ВС

а) Многомодовый ступенчатый ВС;

б) Многомодовый градиентный ВС;

в) одномодовый ВС.

7.3. Основные положения волновой теории ВС

Анализ процессов в ВС в рамках лучевой теории позволяет получить некоторые результаты, но он не даёт представления о всех особенностях распространения света, как электромагнитной волны.

Методика анализа ВС, аналогична методике анализа распространения волн в круглом волноводе.

В ВС присутствуют только токи смещения, а токи проводимости равны нулю. В световоде кроме волн Е и Н распространяются гибридные моды типа и , для которых и одновременно. Решение волнового уравнения представляется функциями Бесселя, а условие распрстранения той или моды определяется обращением в нуль функцией Бесселя (Е - волны) или её производных (Н - волны).

В волоконных световодах, как и в волноводах, распространяется дискретный набор лучей. Каждому лучу соответствует определённая структура поля, которая определяет тип волны – моду. Чем чаще луч отражается от границы сердцевина/оболочка, тем сложнее структура поля, тем выше порядок моды. При определённых условиях в ВС распространяется только один луч осевой и, соответственно, одна мода. Такой ВС называется одномодовым. Условие распространения одной моды

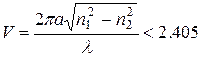, (7.5)

где – длина волны оптической несущей.

Границы отсечки той или иной моды определяются значениями параметра V. Этот параметр называется нормированной критической частотой. Множество дискретных значений V, определяющих возможность существования той или иной моды совпадает с множеством корней цилиндрических функций, при этом порядок цилиндрической функции m определяет число вариаций поля по азимуту, а порядок корня цилиндрической функции – по диаметру ВС. На рис. 7.7 приведены графики функцийБесселя J₀ и J₁, а в таблице 2.1— первые четыре корня функций J₀ и J₁.

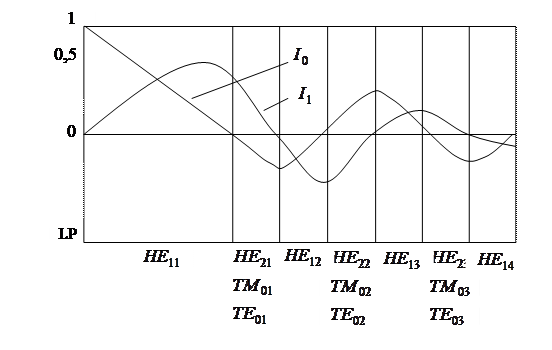
Рис. 7.7. Функции Бесселя нулевого (J₀) и первого (J₁) порядков

Корни функций Бесселя опреде­ляют критические значения пара­метра V_кр, который в этом случае называется норми­рованной критической частотой, он позволяет определить критические длины волн симметричных мод , которые соответствуют критическим режимам. Дляраспространяющейся моды должно выполняться условие , т. е. V>V_0n , причём один из индексов всегда равен нулю.

Симметричные волны порождаются меридиональными лучами, это волны и . Гибридные волны образуются косыми лучами.

Таблица 7.1 – Нули функции

	n
т	1	2	3	4
0	2,405	5,520	3,654	11,790
1	0	3,832	7,016	10,173

Каждая из этих мод имеет критическое значение нормированной частоты V_mn=P_mn, m=1,2,3,…, n=1,2,3,..., a при заданных параметрах ВС критическая длина волны определяется по формуле

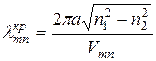. (2.33)

Нормированная критическая частота даёт возможность определить тип распространяющихся мод. ВС, по которому распространяется только одна мода, называется одномодовым, в противном случае многомодовым.

Из рис. 7.7 и таблицы 2.1 видно, что среди направляемых мод особое положение занимает мода НЕ₁₁, у которой т.е. эта мода имеет длины волны отсечки.

Это основная мода ступенчатого ВС, она существует и распространяется при любой длине волны и конструктивных параметрах ВС. С точки зрения геометрической оптики основная мода образуется осевым лучом, т.к. только в этом случае характеристики распространения осевого луча не зависят от условий отражения на границе сердцевина–оболочка. Азимутальная симметрия ВС приводит к поляризационному вырождению этой моды, т.е. в ВС всегда распространяется не одна, а две основные моды с одинаковой структурой поля, плоскости поляризации которых взаимно перпендикулярны. Любое нарушение осевой симметрии (например, эллиптичность сердцевины) приводит к различию коэффициентов фаз мод, т.е. к модовой поляризационной дисперсии.

С увеличением нормированной частоты появляется возможность существования других направляемых мод, которые принято называть высшими. При V ≥ 2.405 начинают распространяться моды H₀₁ и Е₀₁, при V ≥ 2.443 появляется мода НЕ и т.д. (рис. 7.7). Таким образом, можно определить границу одномодового режима: V< 2.405. Исходя из этого значения V можно определить конструктивные параметры одномодового ВС для какой-либо длины волны оптической несущей, и наоборот. Число распространяющихся мод, как это следует из рис. 7.7 и таблицы 7.1, резко возрастает с увеличением V и приближенно может быть определено по формуле для ступенчатого ВС

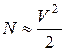. (7.7)

В настоящее время в технике ВОСП для систем с высокой скоростью передачи используются в основном одномодовые. волокна, т.е. волокна, в которых распространяется один тип волны. Многомодовый режим работы ВС приводит к такому нежелательному явлению, как уширение импульсов. Множество типов волн, распространяющихся по ВС, называется "континуумом мод". Некоторое представление о континууме мод дает рис. 7.7. На рис. 7.8 представлены распределения полей для некоторых мод ВС. Для градиентного ВС с параболическим ППП множество распространяющихся мод определяется

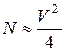. (7.8)

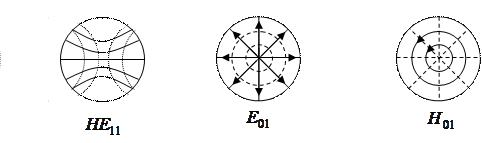
Рис. 7.8. Структура поля некоторых мод в ВС

Из (7.7) и (7.8) видно, что при одинаковой нормированной частоте число направляемых мод в градиентных ВС в 2 раза меньше, чем в ступенчатых. Следует отметить, что градиентные ВС применяются только в многомодовых световодах, где их преимущества существенны. При распространении по ВС большого числа мод полная картина распространения поля будет сложной композицией всех этих мод, в результате чего образуется интерференционная структура. Такая структура наблюдается на выходе многомодовоговолокна при вводе в него когерентного излучения. В одномодовых ВС излучение происходит с части поверхности, которая называется модовым пятном.

7.4. Дисперсия в световодах

С количеством мод, которые распространяются вдоль ВС, связано такое важное понятие как дисперсия. Дисперсия приводит к расширению оптических импульсов, которыми передается информация рис.7.9). Уширение импульсов определяется как

.

Рис. 7.9. Уширение импульсов в ВС

Уширение импульсов вызывает их перекрытие или даже слияние, что приводит к появлению ошибки при передаче импульсных последовательностей. Дисперсия является погонным параметром, измеряется на длину линии в км.

Дисперсия обусловлена такими факторами:

• разностью скоростей модовых составляющих или лучей в ВС (межмодовая дисперсия);
• зависимостью скорости распространения света от длины волны оптической несущей;
• зависимостью показателя преломления от длины волны.

Cоставляющие дисперсии приведены на рисунке 2.28.

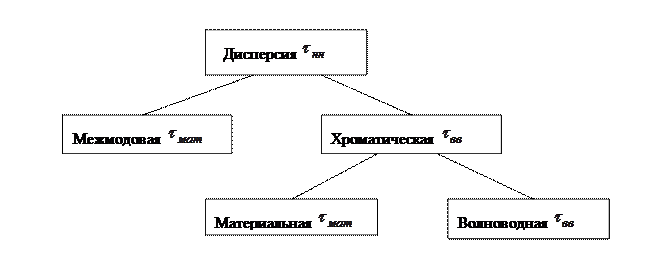
Рис. 7.10. Виды дисперсии

Смысл межмодовой дисперсии легко понять с рис.7.6 а. Оптический импульс передается множеством лучей, каждый с которых по длине ВС, многократно отражаясь от границы сердцевине/оболочка, проходит разный путь. Кратчайший путь имеет осевой луч, время его распространения меньше, чем время распространения лучей, которые образуют моды высшего порядка. Поэтому увеличивается длительность оптического импульса. В одномодовых волокнах межмодовая дисперсия отсутствует (рис. 7.6 в).

Волноводная и материальная дисперсии образуют хроматическую дисперсию.

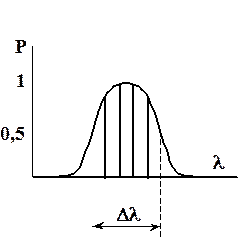
Рис. 7.11. Спектр оптического излучателя

Этот вид дисперсии присутствует как в одномодовых, так и многомодовых волокнах. Он обусловлен тем, что ширина спектра оптического излучателя не равна нулю (рис. 7.11), он имеет множество составляющих. Каждая составляющая распространяется по ВС со своей скоростью, что и обуславливает волноводную дисперсию.

Кроме того, показатель преломления зависит от длины волны света, это обуславливает материальную дисперсию, потому что скорость распространения света в среде равна . Волокно характеризуется удельной дисперсией, приходящейся на ширину спектра излучения в 1мм, тогда хроматическая дисперсия определяется как

,

где - удельная материальная дисперсия, - удельная волноводная дисперсия, . На рис. 7.12 приведена спектральная зависимость хроматической дисперсии. Следует отметить, что удельная хроматическая дисперсия практически равна нулю на длине волны 1.3 мкм (рис.2.30). Разработаны ВС со смещенной дисперсией (рис.2.25), в которых хроматическая дисперсия отсутствует при =1.55 мкм. Все виды дисперсии объединены соотношением : , (с/км).

Дисперсия ограничивает длину регенерационного участка, поэтому на линиях с высокоскоростными ЦСП большой протяженности используются только одномодовые ВС.

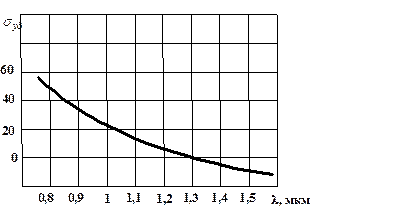
Рис. 7.12. Спектральная зависимость удельной хроматической дисперсии

Дисперсия и затухание являются параметрами передачи оптических кабелей.

7.5. Затухание в волоконных световодах

Одним из основных требований, предъявляемых к любой системе передачи, является большая длина участка регенерации, которая определяется потерями в среде передачи. Поэтому важнейшим параметром ВС является его затухание. Затухание ВС зависит от нескольких факторов, и, в первую очередь, от материала световода и длины волны излучения. В таблице 7.2 приведены значения коэффициентов светоослабления (затухания) различных сред, а также для сравнения даны коэффициенты затухания кабелей и атмосферы. .

Из приведенных данных следует, что оптическое волокно имеет достаточно малое затухание, которое зависит от длины волны излучения. На рис. 7.13 приведена спектральная зависимость затухания, на которой ярко выражены минимумы затухания в некоторых диапазонах длин волн. Эти диапазоны длин волн называются окнами прозрачности ВС. Центральные длины волн в этих окнах составляют: 0,85 мкм для первого, 1,3 мкм для второго и 1,55 мкм для третьего окон прозрачности. Первоначально для практического применения было освоено первое окно прозрачности, т.к. уже в середине 70-х годов существовали источники оптического излучения с длиной волны 0,85 мкм, это красная граница видимого спектра. В настоящее время освоены второе и третье окна прозрачности (невидимое излучение) и ведутся работы по освоению ближнего инфракрасного диапазона ( =2–4 мкм). Освоение этого диапазона позволит несколько увеличить диаметр сердцевины одномодового ВС, что упростит технологию производства ВС.

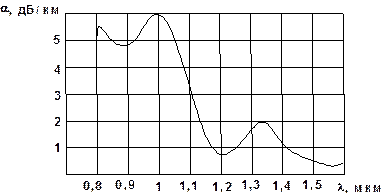
Рисунок 7.13. Спектральная зависимость затухания ВС

Таблица 7.2. Затухание для различных сред передачи

Среда распространения	, дБ/км	, мкм
Обычное силикатное стекло	3000	0.4–0.8
Многокомпонентное стекло	30	0.4–0.8
Кварцевое волокно	7	0.85
Кварцевое волокно	2	1.3
Кварцевое волокно	0.5	1.55
Волокна на основе циркониевых стекол	0.01–0.005	2–10.6
Полимерные волокна	200–400	0.4–1.5
Атмосфера	10	0.85
Симметричный кабель	2–5	–
Коаксиальный кабель	8–13	–

Основными причинами возникновения потерь в ВС являются поглощение и рассеяние энергии. Потери вследствие поглощения подразделяются на собственные и несобственные. Собственное поглощение вызвано взаимодействием распространяющейся световой волны с компонентами материала световода и оболочки, не содержащего примесей. Поглощение энергии в этом случае ведет к квантовым переходам между различными электронными и молекулярными энергетическими уровнями вещества. Эти явления носят резонансный характер, чем объясняются всплески на кривых (рис. 7.13).

Несобственное поглощение обусловлено наличием примесей даже в ничтожном количестве, исчисляемом иногда единицами атомов примеси на миллион атомов собственного вещества. Особенно значительное поглощение вызывает наличие ионов некоторых металлов (медь, хром, железо, никель) и наличие в материале ионов гидроксильных групп ОН. Основным механизмом этих потерь является резонансное поглощение энергии атомами и ионами примесей на различных длинах волн.

В общем случае в BС в режиме линейной оптики (при малых значениях оптической мощности) наблюдается три основных вида рассеяния: рэлеевское, молекулярное и лучевое. Фундаментальным линейным эффектом является рассеяние Рэлея. Это рассеяние не зависит от интенсивности света. Оно обусловлено микролокальнымифлюктуациями показателя преломления вещества, которые, в свою очередь, возникают за счет микроскопических неоднородностей в материале, т.к. стекло имеет аморфную, а не кристаллическую структуру. Эти неоднородности намного меньше длины волны и растут пропорционально . Эти потери являются неустранимыми.

Увеличение числа компонентов в стекле для формирования необходимого профиля показателя преломления увеличивает рэлеевское рассеяние. Кварцевое стекло имеет минимальные потери на рэлеевском рассеянии.

Полное затухание в материале волоконного световода определяется суммой потерь

; ; ,

где - потери вследствие поглощения; - потери вследствие рассеяния; - собственные потери; - потери рэлеевского рассеяния; - потери молекулярного рассеяния; - потери лучевого рассеяния.

Лучевое рассеяние возникает на крупных частицах, размеры которых больше длины волны излучения. Молекулярное рассеяние возникает на частицах соизмеримых с длиной волны оптической несущей.

Кроме этих потерь в кабеле возникают дополнительные - кабельные потери. При производстве волокна и в процессе его укладки в кабель возникают микро- и макроизгибы. Микроизгибы – это искажения прямолинейности оптического волокна в процессе его производства, макроизгибы возникают при укладке ОВ в кабель. Механизм потерь при микро- и макроизгибах ясен из рис. 7.14. На микроизгибах возникает рассеяние свет, на макроизгибах нарушается условие полного внутреннего отражения.

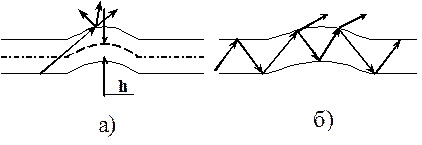
Рис. 7.14. Механизм потерь на микроизгибах а) и макроизгибах б)

Вопросы и задания для самоконтроля

1.     В каком диапазоне волн используются ВС?

2.     Охарактеризуйте преимущества ВС.

3.     Объясните явление полного внутреннего отражения.

4.     Объясните принцип действия ВС.

5.     Дайте определение апертурного угла и числовой апертуры.

6.     Приведите расчёт числовой апертуры.

7.     Приведите профили показателей преломления ВС.

8.     Объясните ход лучей в одномодовом ВС, в многомодовом градиентном и ступенчатом.

9.     Что такое нормированная частота, какой её смысл?

10.           Что такое одномодовый и многомодовый ВС?

11.           Какие типы волн распространяются в ВС?

12.           Объясните явление уширения импульсов. Чем оно вызвано?

13.           Охарактеризуйте виды дисперсии.

14.           Что такое окна прозрачности ВС, каким длинам волн и затуханием они соответствуют?

15.           Чем вызваны дополнительные потери в ВС?

Письменные задания

1.     Получите расчётную формулу для межмодовой дисперсии.

2.     Определите диаметр одномодового ВС в каждом их окон прозрачности, если .

3.     При каком апертурном угле в стандартном многомодовом ВС будет распространяться только один тип волны?

4.     Определите количество волн в световоде с параметрами мкм; в каждом из окон прозрачности.

5.     Нормированная критическая частота ВС . Определите, какие моды распространяются в ВС.

6.     Определите диаметр ВС, в котором будет распространяться 4 моды для третьего окна прозрачности, если .