Цифровым фильтром называется физическое устройство или программа вычислений на ЭВМ, реализующее преобразование (8.32) или, что то же самое, алгоритм цифровой фильтрации.

Физически осуществимые цифровые фильтры, которые работают в реальном масштабе времени для формирования выходного сигнала в -тый дискретный момент времени могут использовать данные двух типов

– текущий и некоторое количество предыдущих отсчетов входного сигнала;

– помимо текущего и некоторого количества предыдущих отсчетов входного сигнала еще и некоторое количество предыдущих отсчетов выходного сигнала.

Целые числа и , причем определяют порядок цифрового фильтра.

Фильтры, использующие для формирования выходного сигнала только отсчеты входного сигнала, получили название трансверсальных фильтров. Фильтры же, использующие для формирования выходного сигнала не только отсчеты входного, но предыдущие отсчеты выходного сигнала называются рекурсивными цифровыми фильтрами.

Начнем с рассмотрения трансверсальных (нерекурсивных) фильтров. Так как в таких фильтрах текущий отсчет выходного сигнала определяется только отсчетом входного сигнала, алгоритм фильтрации как это следует из (8.32) записывается следующим образом

. (8.47)

Здесь – порядок трансверсального фильтра.

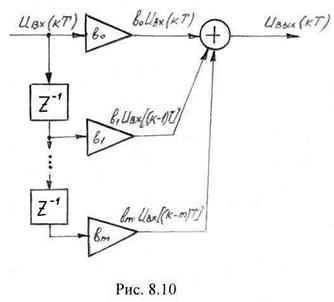
Структурная схема трансверсального фильтра изображена на рис. 8.10. Основными элементами фильтра служат элементы задержки отсчетных значений входного сигнала на один интервал дискретизации (прямоугольники ) и перемножители (прямоугольники), осуществляющие перемножение соответствующих отсчетных значений на масштабные коэффициенты , где . С выходов перемножителей сигналы поступают на сумматор, где складываясь, образуют отсчет выходного сигнала . Нетрудно убедиться, что трансверсальный фильтр представляет собой дискретную цепь без обратной связи.

Отметим, что элемент задержки га один такт обозначен через на основании (8.45), из которого следует, что при задержке последовательности на один такт ее преобразование умножается на .

Рассмотрим характеристики трансверсального фильтра. Импульсная характеристика, как было определено выше, представляет собой отклик фильтра на входной сигнал вида (выражение (8.34)). Ранее, уже была определена импульсная характеристика дискретной цепи, описываемой уравнением (8.35), что полностью соответствует (8.47) – уравнению трансверсального фильтра. Импульсная характеристика представляет собой последовательность чисел:

.

В этом нетрудно убедится, рассматривая работу схемы, изображенной на рис. 8.10. В начальный момент времени и сигнал на выходе . В следующий момент времени с номером такта задержанный на длительность такта единичный импульс умножится на масштабный коэффициент и выходной сигнал будет равен и т.д. Отметим, что в реальных физически реализуемых фильтрах его порядок представляет собой конечное число. А это значит, что импульсная характеристика фильтра является конечной последовательностью. Поэтому, трансверсальные фильтры имеют еще одно название – фильтры с конечной импульсной характеристикой или КИХ – фильтры.

Системная функция. Применим к (8.47) -преобразование:

,

откуда

. (8.48)

Таким образом, системная функция трансверсального фильтра является дробно-рациональной функцией.

Комплексный коэффициент передачи. Производя в (8.47) замену , получим выражение для комплексного коэффициента передачи:

. (8.49)

Очевидно, из (8.49) можно получить выражения для амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристик. При заданном шаге дискретизации можно реализовать самые разнообразные формы АЧХ, подбирая должным образом коэффициенты .

Трансверсальные фильтры получили широкое распространение вследствие простоты реализации. Вместе с тем, для получения хороших частотных характеристик необходимы фильтры высокого порядка ( достигает величины несколько сотен). Это сдерживает применение трансверсальных фильтров.

Если для формирования текущего отсчета выходного сигнала используются предыдущие отсчеты как входного, так и выходного сигналов, такие фильтры, как подчеркивалось выше, называются рекурсивными.

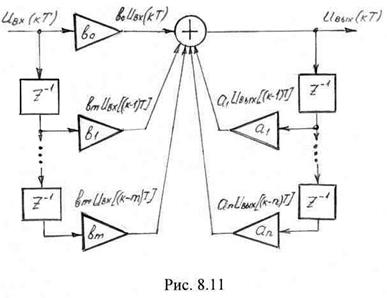В общем случае рекурсивный фильтр описывается линейным разностным уравнением (8.32), а схема устройства, реализующего алгоритм фильтрации (8.32) изображена на рис. 8.11.

Как следует из рисунка рекурсивный фильтр содержит нерекурсивную часть, идентичную рассмотренному выше трансверсальному фильтру и рекурсивную часть , состоящую из линии задержки и перемножителей на масштабные коэффициенты . Рекурсивная часть фильтра использует предшествующих значений выходного сигнала для формирования его текущего значения. Таким образом, рекурсивный фильтр является дискретной линейной цепью с обратной связью.

Рассмотрим основные характеристики рекурсивного фильтра.

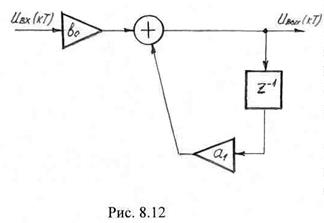
Импульсная характеристика. Так как рекурсивный фильтр представляет собой дискретную цепь с обратной связью следует ожидать, что его импульсная характеристика имеет характер бесконечной последовательности. Убедимся в этом на примере цепи, описываемой уравнением (8.31), структурная схема которой представлена на рис. 8.12.

Очевидно, рассматриваемая цепь представляет собой рекурсивный фильтр первого порядка. Пусть входной сигнал представляет собой единичный импульс, т.е. . Рассмотрим по тактам последовательность отсчетов на выходе фильтра.

При , ;

при , ;

при ,

при , и т.д.

Таким образом, импульсная характеристика фильтра:

, (8.50)

представляет собой геометрическую прогрессию, убывающую при . Подобная ситуация имеет место для любого рекурсивного фильтра. Поэтому рекурсивные фильтры получили также название фильтров с бесконечной импульсной характеристикой или БИХ - фильтров.

Системная функция. Применяя к (8.32) -преобразование можно получить выражение для системной функции рекурсивного фильтра

. (8.51)

Комплексный коэффициент передачи определяется из (8.51) заменой

, (8.52)

откуда можно получить выражения для АЧХ и ФЧХ рекурсивного фильтра.

Достоинством рекурсивных фильтров является то, что рекурсивные фильтры позволяют получить хорошие частотные характеристики при меньшем значении порядка фильтра по сравнению с трансверсальными. Поскольку порядок фильтра определяет объем памяти (длину линии задержки), то рекурсивные фильтры требуют меньшего объема памяти, а следовательно меньшего объема вычислений. В то же время, поскольку рекурсивные фильтры являются цепями с обратной связью, они менее устойчивы, чем трансверсальные фильтры.