Реальные сигналы всегда имеют конечную длительность и ограниченную полосу частот. Граничные частоты спектра определяются свойствами системы передаче и самим получателем. Так, при передаче дискретных сообщений полоса частот определяется скоростью передачи, при передаче телевизионного изображения — принятым стандартом четкости (числом строк) и т. д.

Для функций с ограниченным спектром В. А. Котельников доказал замечательную теорему, лежащую в основе дискретизации непрерывных сигналов. Согласно этой теореме функция f(t), не содержащая частот выше F, полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга на , сек.

Доказательство теоремы состоит в следующем. Пусть функция f(t) имеет ограниченный спектр:

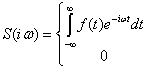
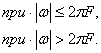
На конечном интервале .(-2πF,2πF) функцию S(iω) можно представить в виде ряда Фурье по аргументу ω. Согласно (2.67) имеем

Коэффициенты Фурье в этом случае запишутся в виде

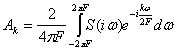
Так как S(iω) есть преобразование Фурье для f(t), то обратно f(t) есть преобразование Фурье для S(iω):

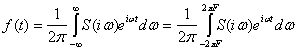
так как S(iω) равно нулю вне указанных пределов. Если положить t= получим

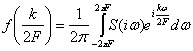
Сравнивая полученное выражение с выражением для , видим, что

Следовательно,

Так как f(t) однозначно определяется своим спектром S(iω), то из полученного соотношения следует, что f(t), как иS(iω), однозначно определяется отсчетами f(kΔt). Это и доказывает теорему Котельникова.

Выражая функцию f(t) через ее спектр S(iω), получим

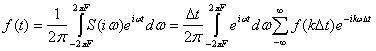
или, изменяя порядок действия,

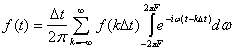
Отсюда после интегрирования находим

(2.92)

Полученное выражение представляет собой разложение непрерывной функции f(t) в ряд по ортогональным функциям вида Величины f(kΔt) называются отсчетами функции f(t). Они определяют значения исходной функции f(t) в дискретные моменты времени kΔt. Множитель называется функцией отсчетов. Если обозначить τ=t—kΔt, то функция отсчетов примет вид

(2.93)

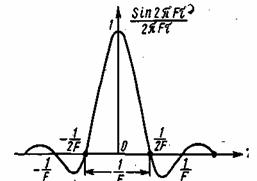
Рис. 2.8. Функция отсчетов

График этой функции приведен на рис. 2.8. Функция отсчетов принимает наибольшее значение, равное единице, в моменты времени t=kΔt(=0) и обращается в нуль в моменты времени t=(k±m)Δt где т-1,2, Ширина главного лепестка функции отсчетов на нулевом уровне равна 1/F. Спектр функции отсчетов является равномерным в полосе (-FdF,) и равен нулю вне этой полосы. Действительно,

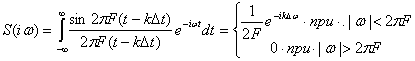
Модуль Энергия сигнала через отсчетные значения выражается следующим образом:

(2.94)

Если полоса частот сигнала f(t) неограниченно расширяется, то Δt будет неограниченно уменьшаться и в пределе при функция отсчетов стремится к дельта-функции), а ряд Котельникова (2.92) превращается в интеграл

(2.95)

Свертка дельта-функции с любой функцией f(t) дает равенство

из которого видно, что интеграл (2.95) не изменится от замены функции f(t) ее значением . Следовательно, (2.95) преобразовывается в интеграл Дюмеля, который обычно записывается

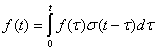(2.96)

Вернемся к выражению ряда Котельникова (2.92). Каждое слагаемое этого разложения по физическому смыслу представляет отклик идеального фильтра нижних частот, с частотой среза F на весьма короткий импульс, приходящий в момент и имеющий площадь, равную мгновенному значению функции f(t) в тот же момент. Отсюда следует, что при передаче сигнала f(t) с ограниченным спектром по каналу связи необходимо через равные интервалы Δt=1/2F взять отсчеты мгновенных значений сигнала и передать по каналу короткие импульсы, площади которых пропорциональны этим отсчетам. На приемном конце эти импульсы пропускаются через фильтр нижних частот и тем самым восстанавливается исходный сигнал f(t) как сумма откликов фильтра.

Сигнал конечной длительности Т, очевидно, будет определяться v== 2TF отсчетами. Строго говоря, не может существовать функции, ограниченной во времени и одновременно обладающей ограниченным спектром. Однако возможно существование функции, для которой почти вся энергия сосредоточена в конечном интервале времени ,и ограниченной полосе частот. Сигналы связи в большинстве случаев являются функциями такого типа. В этом случае разложение в ряд Котельникова будет давать некоторую погрешность ~, где Е — полная энергия сигнала и ΔE энергия той части спектра сигнала, которая расположена вне полосы F. При разложении сигнала в ряд Фурье мы тоже получили v=2TF. Таким образом, сигнал с ограниченным спектром F и конечной длительностью. Т определяется 2TF числами независимо от того, что собой представляют эти числа — мгновенные ли значения сигнала в точках отсчета либо спектральные коэффициенты разложения в ряд Фурье.

Теорема Котельникова позволяет единым образом рассматривать передачу любого сигнала (дискретного и непрерывного) как передачу чисел. Эта теорема лежит в основе всех видов импульсной модуляции. Согласно этой теореме необходимая частота следования импульсов F, называемая тактовой частотой, должна определяться из условия, где Fm — верхняя граничная частота спектра передаваемого сообщения.

Теорема Котельникова может быть обобщена и на случай функций, спектр которых не начинается с нулевой частоты. В формулировке автора эта теорема гласит: «Любую функцию f(t), состоящую из частот от f до f, можнo передавать с любой точностью при помощи чисел, передаваемых друг за другом через , сек. В этом случае функция f(t) на оси времени определяется через интервалы , где F=.При этом в каждой точке отсчитываются две величины: амплитуда и фаза. Если длительность сигнала равна Т, то количество отсчетных точек на оси времени

равно =TF, а общее количество отсчетов (амплитуд и фаз) равно v=2FT. Функцию f(t), ограниченную частотами f и f можно представить следующим рядом:

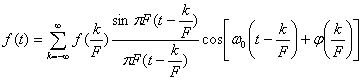(2.97)

где и отсчетные значения соответственно амплитуды и фазы сигнала;среднее значение круговой частоты спектра сигнала. Функция отсчетов в этом случае представляет собой модулированное колебание с несущей, равной , и огибающей, определяемой функцией вида