7.2.1. Представление связи

7.2.1.1. Реакция кодера на импульсное возмущение

7.2.1.2. Полиномиальное представление

7.2.2. Представление состояния и диаграмма состояний

7.2.3. Древовидные диаграммы

7.2.4. Решетчатая диаграмма

Чтобы иметь возможность описывать сверточный код, необходимо определить кодирующую функцию G(m) так, чтобы по данной входящей последовательности m можно было быстро вычислить выходную последовательность U. Для реализации сверточного кодирования используется несколько методов; наиболее распространенными из них являются графическая связь, векторы, полиномы связи, диаграмма состояния, древовидная и решетчатая диаграммы. Все они рассматриваются ниже.

7.2.1. Представление связи

При обсуждении сверточных кодеров в качестве модели будем использовать сверточный кодер, показанный на рис. 7.3. На этом рисунке изображен сверточный кодер (2,1) с длиной кодового ограничения K = 3. В нем имеется n =2 сумматора по модулю 2; следовательно, степень кодирования кода k/n равна 1/2. При каждом поступлении бит помещается в крайний левый разряд, а биты регистра смещаются на одну позицию вправо. Затем коммутатор на выходе дискретизирует выходы всех сумматоров по модулю 2 (т.е. сначала верхний сумматор, затем нижний), в результате чего формируются пары кодовых символов, образующих ответвленное слово, связанное с только что поступившим битом. Эта выполняется для каждого входного бита. Выбор связи между сумматорами и разрядами регистра влияет на характеристики кода. Всякое изменение в выборе связей приводит в результате к различным кодам. Связь, конечно же, выбирается и изменяется не произвольным образом. Задача выбора связей, дающая оптимальные дистанционные свойства, сложна и в общем случае не решается; однако для всех значений длины кодового ограничения, меньших 20, с помощью компьютеров были найдены хорошие коды [3-5].

В отличие от блочных кодов, имеющих фиксированную длину слова n, в сверточных кодах нет определенного размера блока. Однако с помощью периодического отбрасывания сверточным кодам часто принудительно придают блочную структуру. Это требует некоторого количества нулевых разрядов, присоединенных к концу входной последовательности данных, которые служат для очистки (или промывки) регистра сдвига от бит данных. Поскольку добавленные нули не несут дополнительной информации, эффективная степень кодирования будет ниже k/n. Чтобы степень кодирования оставалась близкой к k/n, период отбрасывания чаще всего делают настолько большим, на сколько это возможно.

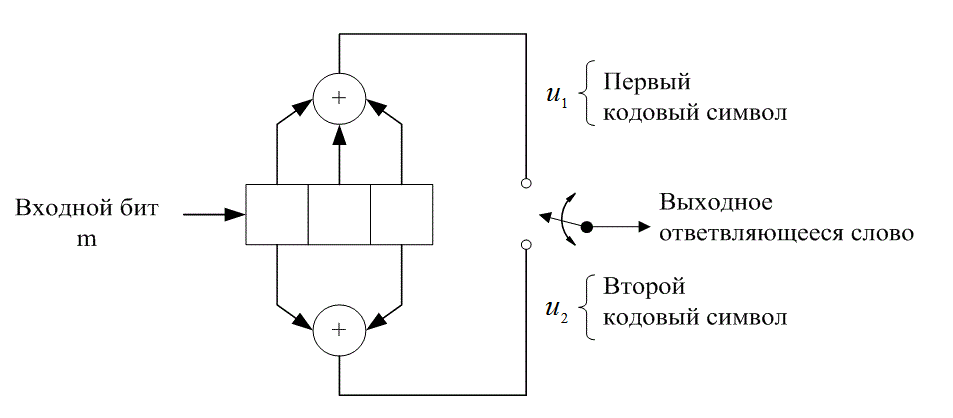
Рис. 7.3. Сверточный кодер (степень кодирования 1/2, К= 3)

Один из способов реализации кодера заключается в определении п векторов связи, по одному на каждый из п сумматоров по модулю 2. Каждый вектор имеет размерность K и описывает связь регистра сдвига кодера с соответствующим сумматором по модулю 2. Единица на i-й позиции вектора указывает на то, что соответствующий разряд в регистре сдвига связан с сумматором по модулю 2, а нуль в данной позиции указывает, что связи между разрядом и сумматором по модулю 2 не существует. Для кодера на рис. 7.2 можно записать вектор связи для верхних связей, а — для нижних.

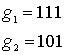
Предположим теперь, что вектор сообщения m = 1 0 1 закодирован с использованием сверточного кода и кодера, показанного на рис. 7.3. Введены три бита сообщения, по одному в момент времени , как показано на рис. 7.4. Затем для очистки регистра в моменты времени и введены нуля, что в результате приводит к смещению конечного участка на всю длину регистра. Последовательность на выходе выглядит следующим образом: 1110001011, где крайний левый символ представляет первую передачу. Для декодирования сообщения нужна полная последовательность на выходе (включающая кодовые символы). Для удаления сообщения из кодера требуется на единицу меньше нулей, чем имеется разрядов в регистре, или очищенных бит. В момент времени показан нулевой выход, это должно дать читателю возможность убедиться в том, что в момент времени регистр устанавливается в исходное состояние. Таким образом, в момент времени уже можно передавать новое сообщение.

7.2.1.1. Реакция кодера на импульсное возмущение

Мы можем описать кодер через его импульсную характеристику, т.е. в виде отклика кодера на единичный проходящий бит. Рассмотрим содержимое регистра (рис. 7.3) при прохождении через него двоичной единицы.

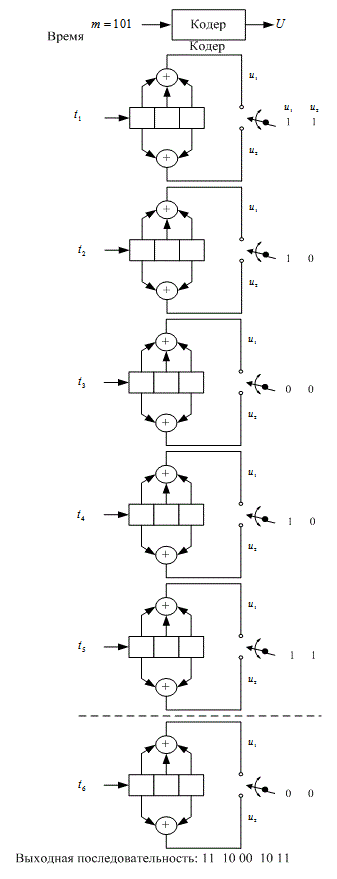
Рис. 7.4. Сверточное кодирование последовательности сообщения со степенью кодирования 1/2 кодером с К=3.

Ответвляющееся слово

	Содержимое регистра
	100	1	1
	010	1	0
	001	1	1
Входная последовательность	1 0 0
Выходная последовательность	11 10 11

Последовательность на выходе при единице на входе называется откликом кодера на импульсное возмущение, или его импульсной характеристикой. Для входной последовательности m = 1 0 1 данные на выходе могут быть найдены путем суперпозиции или линейного сложения смещенных во времени входных "импульсов".

Вход, m Выход

1	11	10	11
0		00	00	00
1		11	11	10	11
Сумма по модулю 2	11	00	00	10	11

Обратите внимание на то, что эти данные на выходе такие же, как и на рис. 7.4, что указывает на линейность сверточных кодов — точно так же как и в блочных кодах в главе 6. Название сверточный кодер (convolutional encoder) возникло именно вследствие этого свойства генерации данных на выходе с помощью линейного сложения (или свертки) смещенных во времени импульсов последовательности на входе с импульсной характеристикой кодера. Такие устройства часто описываются с помощью матричного генератора бесконечного порядка [6].

Отметим, что в рассмотренном выше примере входящей последовательности из 3 бит и последовательности на выходе из 10 бит эффективная степень кодирования составляет k/n = 3/10, что значительно меньше величины 1/2, которую можно было бы ожидать, зная, что каждый бит данных на входе порождает пару канальных битов на выходе. Причина этого заключается в том, что окончательные биты данных нужно проводить через кодер. Все канальные биты на выходе нуждаются в процессе декодирования. Если бы сообщение было длиннее, скажем 300 бит, последовательность кодовых слов на выходе содержала бы 640 бит и значение для степени кодирования кода 300/640 было бы значительно ближе к 1/2.

7.2.1.2. Полиномиальное представление

Иногда связи кодера описываются с помощью полиномиального генератора, аналогичного используемому в главе 6 для описания реализации обратной связи регистра сдвига циклических кодов. Сверточный кодер можно представить в виде набора из п полиномиальных генераторов, по одному для каждого из п сумматоров по модулю 2. Каждый полином имеет порядок или меньше и описывает связь кодирующего регистра сдвига с соответствующим сумматором по модулю 2, почти так же как и вектор связи. Коэффициенты возле каждого слагаемого полинома порядка (K - 1) равны либо 1, либо 0, в зависимости от того, имеется ли связь между регистром сдвига и сумматором по модулю 2. Для кодера на рис. 7.3 можно записать полиномиальный генератор для верхних связей и— для нижних.

Здесь слагаемое самого нижнего порядка в полиноме соответствует входному разряду регистра. Выходная последовательность находится следующим образом.

чередуется с

Прежде всего, выразим вектор сообщения m = 1 0 1 в виде полинома, т.е. . Для очистки регистра мы снова будем предполагать использование нулей, следующих за битами сообщения. Тогда выходящий полином U(X), или выходящая последовательность U кодера (рис. 7.3) для входящего сообщения m может быть найдена следующим образом.

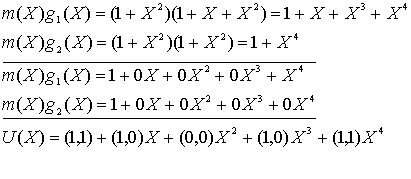
В этом примере мы начали обсуждение с того, что сверточный кодер можно трактовать как набор регистров сдвига циклического кода. Мы представили кодер в виде полиномиальных генераторов, с помощью которых описываются циклические коды. Однако мы пришли к той же последовательности на выходе, что и на рис. 7.4, и к той же, что и в предыдущем разделе, полученной при описании реакции на импульсное возмущение. (Чтобы иметь лучшее представление о структуре сверточного кода в контексте линейной последовательной схемы, обратитесь к работе [7].)

7.2.2. Представление состояния и диаграмма состояний

Сверточный кодер принадлежит классу устройств, известных как конечный автомат (finite-state machine). Это общее название дано системам, обладающим памятью о прошедших сигналах. Прилагательное конечный показывает, что существует ограниченное число состояний, которое может возникнуть в системе. Что имеется в виду под состоянием (state) в системах с конечным его числом? В более общем смысле состояние включает наименьшее количество информации, на основе которой вместе с текущими входными данными можно определить данные на выходе системы. Состояние дает некоторое представление о прошлых событиях (сигналах) и об ограниченном наборе возможных выходных данных в будущем. Будущие состояния ограничиваются прошлыми состояниями. Для сверточного кода со степенью кодирования 1/n состояние представлено содержимым K - 1 крайних правых разрядов (рис. 7.4). Знание состояния плюс знание следующих данных на входе является необходимым и достаточным условием для определения данных на выходе. Итак, пусть состояние кодера в момент времени определяется как , i-я ветвь кодовых слов полностью определяется состоянием и введенными в настоящее время битами ; таким образом, состояние описывает предысторию кодера для определения данных на его выходе. Состояния кодера считаются Марковскими в том смысле, что вероятность нахождения в состоянии , определяемая всеми предыдущими состояниями, зависит только от самого последнего состояния , т.е. она равна .

Одним из способов представления простых кодирующих устройств является диаграмма состояния (state diagram); такое представление кодера, изображенного на рис. 7.3, показано на рис. 7.5. Состояния, показанные в рамках диаграммы, представляют собой возможное содержимое K - 1 крайних правых разрядов регистра, а пути между состояниями — ответвляющиеся слова на выходе, являющиеся результатом переходов между такими состояниями. Состояния регистра выбраны следующими: а = 00, b = 10, c = 01 и d = 11 диаграмма, показанная на рис. 7.5, иллюстрирует все возможные смены состояний для кодера, показанного нарис. 7.3. Существует всего два исходящих из каждого состояния перехода, соответствующие двум возможным входным битам. Далее для каждого пути между состояниями записано ответвляющееся слово на выходе, связанное с переходами между состояниями. При изображении путей, сплошной линией принято обозначать путь, связанный с нулевым входным битом, а пунктирной линией — путь, связанный с единичным входным битом. Отметим, что за один переход невозможно перейти из данного состояния в любое произвольное. Так как за единицу времени перемещается только один бит, существует только два возможных перехода между состояниями, в которые регистр может переходить за время прохождения каждого бита. Например, если состояние кодера — 00, при следующем смещении возможно возникновение только состояний 00 или 10.

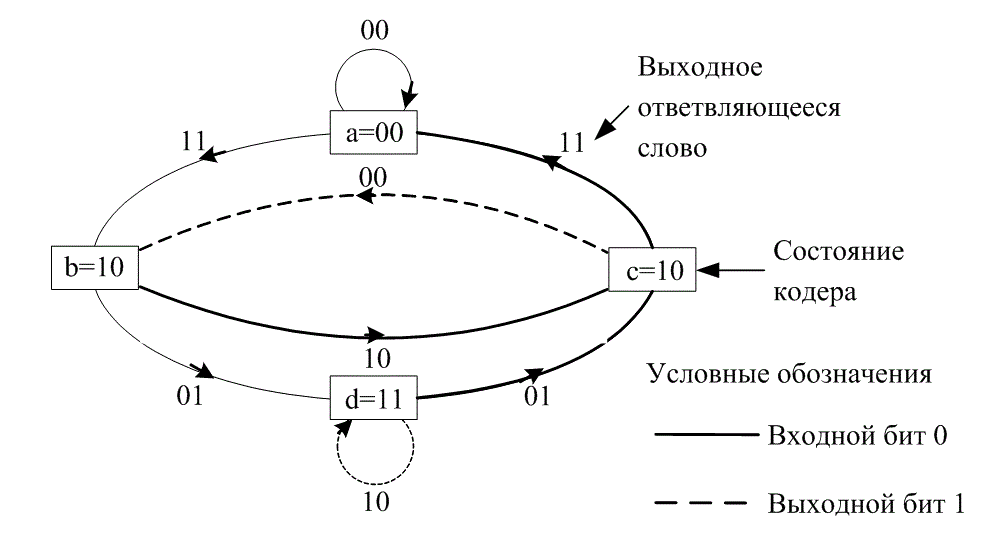
Рис. 7.5. Диаграмма состояний кодера (степень кодирования 1/2, К= 3)

Пример 7.1. Сверточное кодирование

Для кодера, показанного на рис. 7.3, найдите изменение состояний и результирующую последовательность кодовых слов U для последовательности сообщений m = 1 1 0 1 1, за которой следует нуля для очистки регистра. Предполагается, что в исходном состоянии регистр содержит одни нули.

Решение

Ответвляющееся слово в момент времени ()

Ответвляющееся слово в момент времени
Входные Биты,	Содержимое регистра	Состояние в момент времени	Состояние в момент времени
-	000	00	00	-
1	100	00	10	1	1
1	110	10	11	0	1
0	011	11	01	0	1
1	101	01	10	0	1
1	110	10	11	0	1
0	011	11	01	0	1
0	0	01	00	1	1

Последовательность на выходе U= 11 01 01 00 01 01 11

Пример 7.2. Сверточное кодирование

В примере 7.1 исходное содержимое регистра — все нули. Это эквивалентно тому, что данной последовательности на входе предшествовали два нулевых бита (кодирование является функцией настоящих информационных бит и K - 1 предыдущих бит). Повторите задание примера 7.1, предполагая, что данной последовательности предшествовали два единичных бита, и убедитесь, что теперь последовательность кодовых слов U для входящей последовательности т = 1 1 0 1 1 отличается от последовательности, найденной в примере 7.1.

Решение Запись "х" обозначает "неизвестно".

Ответвляющееся слово в момент времени ()

Ответвляющееся слово в момент времени
Входные Биты,	Содержимое регистра	Состояние в момент времени	Состояние в момент времени
-	11	1	11	-
1	111	11	11	1	0
1	111	11	11	1	0
0	011	11	01	0	1
1	101	01	10	0	0
1	110	10	11	0	1
0	011	11	01	0	1
0	0	01	00	1	1

Последовательность на выходе U= 10 10 01 00 01 01 11

Сравнивая эти результаты с результатами из примера 7.1, можно видеть, что каждое ответвленное слово выходной последовательности U является функцией не только входного бита, но и предыдущих бит.

7.2.3. Древовидные диаграммы

Несмотря на то что диаграммы состояний полностью описывают кодер, по сути, их нельзя использовать для легкого отслеживания переходов кодера в зависимости от времени, поскольку диаграмма не представляет динамики изменений. Древовидная диаграмма (tree diagram) прибавляет к диаграмме состояния временное измерение. Древовидная диаграмма сверточного кодера, показанного на рис. 7.3, изображена на рис. 7.6. В каждый последующий момент прохождения входящего бита процедура кодирования может быть описана с помощью перемещения по диаграмме слева направо, причем каждая ветвь дерева описывает ответвленное слово на выходе. Правило ветвления для нахождения последовательности кодовых слов следующее: если входящим битом является нуль, то он связывается со словом, которое находится путем перемещения в следующую (по направлению вверх) крайнюю правую ветвь; если входящий бит — это единица, то ответвленное слово находится путем перемещения в следующую (по направлению вниз) крайнюю правую ветвь. Предполагается, что первоначально кодер содержал одни нули. Диаграмма показывает, что если первым входным битом был нуль, то ответвляющимся словом на выходе будет 00, а если первым входным битом была единица, то ответвляющимся словом на выходе будет 11. Аналогично, если первым входным битом была единица, а вторым — нуль, на выходе вторым ответвляющимся словом будет 10. Если первым входным видом была единица и вторым входным битом была единица, вторым ответвляющимся словом на выходе будет 01. Следуя этой процедуре, видим, что входящая последовательность 11011 представляется жирной линией, нарисованной на древовидной диаграмме (рис. 7.6). Этот путь соответствует выходной последовательности кодовых слов 1101010001. Дополнительное временное измерение в древовидной диаграмме (по сравнению с диаграммой состояния) допускает динамическое описание кодера как функции конкретной входной последовательности. Однако заметили ли вы, что при попытке описания с помощью древовидной диаграммы последовательности произвольной длины возникает проблема? Число ответвлений растет как , где L — это количество ответвляющихся слов в последовательности. При большом L вы бы очень быстро исписали бумагу и исчерпали терпение.

7.2.4. Решетчатая диаграмма

Исследование древовидной диаграммы на рис. 7.6 показывает, что в этом примере после третьего ветвления в момент времени г4 структура повторяется (древовидная структура повторяется после К ответвлений, где К — длина кодового ограничения). Пометим каждый узел в дереве (рис. 7.6), ставя в соответствие четыре возможных состояния в регистре сдвига: а =00, b = 10, с = 01 и d = 11. Первое ветвление древовидной структуры в момент времени дает пару узлов, помеченных как а и b. При каждом последующем ветвлении количество узлов удваивается. Второе ветвление в момент времени дает в результате четыре узла, помеченных как а, b, c и d. После третьего ветвления всего имеется восемь узлов: два — а, два — b, два — с и два — d.

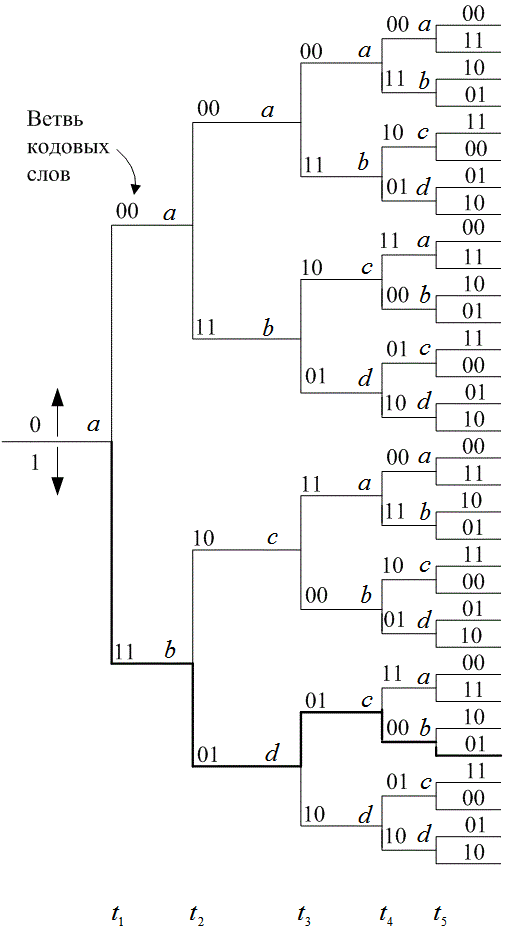
Рис. 7.6. Древовидное представление кодера (степень кодирования 1/2, К = 3)

Можно видеть, что все ветви выходят из двух узлов одного и того же состояния, образуя идентичные ветви последовательностей кодовых слов. В этот момент дерево делится на идентичные верхнюю и нижнюю части. Смысл этого становится яснее после рассмотрения кодера, изображенного на рис. 7.3. Когда четвертый входной бит входит в кодер слева, первый входной бит справа выбрасывается и больше не влияет на ответвленные слова на выходе. Следовательно, входящие последовательности 1 0 0 х у... и 0 0 0х у..., где крайний левый бит является самым ранним, после (К = 3)-го ветвления генерируют одинаковые ответвляющиеся слова. Это означает, что любые состояния, имеющие одинаковую метку в один и тот же момент , можно соединить, поскольку все последующие пути будут неразличимы. Если мы проделаем это для древовидной структуры, показанной на рис. 7.6, получим иную диаграмму, называемую решетчатой. Решетчатая диаграмма, которая использует повторяющуюся структуру, дает более удобное описание кодера, по сравнению с древовидной диаграммой. Решетчатая диаграмма для сверточного кодера, изображенного на рис. 7.3, показана на рис. 7.7

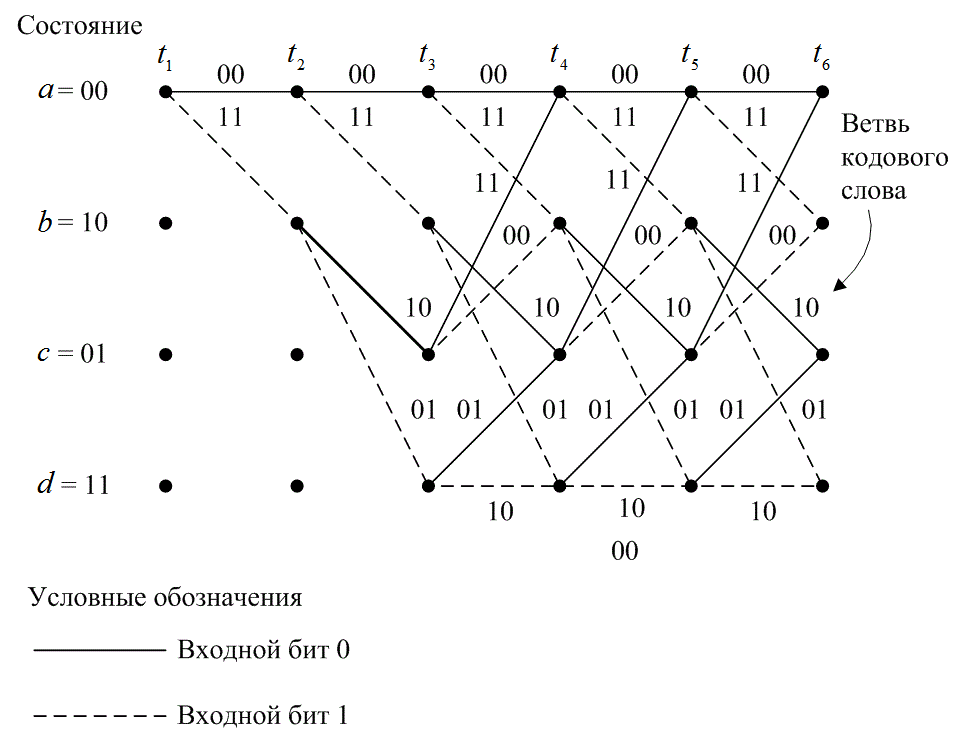
Рис. 7.7. Решетчатая диаграмма кодера (степень кодирования 1/2, К = 3)

При изображении решетчатой диаграммы мы воспользовались теми же условными обозначениями, что и для диаграммы состояния: сплошная линия обозначает выходные данные, генерируемые входным нулевым битом, а пунктирная — выходные данные, генерируемые входным единичным битом. Узлы решетки представляют состояния кодера; первый ряд узлов соответствует состоянию а = 00, второй и последующие — состояниям a = 00, b = 10, с = 01 и d = 11. В каждый момент времени для представления возможных состояний кодера решетка требует узлов. В нашем примере после достижения глубины решетки, равной трем (в момент времени ), замечаем, что решетка имеет фиксированную периодическую структуру. В общем случае фиксированная структура реализуется после достижения глубины K. Следовательно, с этого момента в каждое состояние можно войти из любого из двух предыдущих состояний. Также из каждого состояния можно перейти в одно из двух состояний. Из двух исходящих ветвей одна соответствует нулевому входному биту, а другая — единичному входному биту. На рис. 7.7 ответвляющиеся слова на выходе соответствуют переходам, между состояниями, показанными как метки на ветвях решетки.

Один столбец временного интервала сформировавшейся решетчатой структуры кодирования полностью определяет код. Несколько столбцов показаны исключительно для визуализации последовательности кодовых символов как функции времени. Состояние сверточного кодера представлено содержанием крайних правых разрядов в регистре кодера. Некоторые авторы описывают состояние с помощью крайних левых разрядов. Какое описание правильно? Они оба верны. Каждый переход имеет начальное и конечное состояние. Крайние правые разрядов описывают начальное состояние для текущих входных данных, которые находятся в крайнем левом разряде (степень кодирования предполагается равной 1/n). Крайние левые разрядов являются конечным состоянием для такого перехода. Последовательность кодовых символов характеризуется N ветвями (что представляет N бит данных), занимающими N интервалов времени. Она связана с конкретным состоянием в каждый из N + 1 интервалов времени (от начала до конца). Таким образом, мы запускаем биты в моменты времени и интересуемся метрикой состояния в моменты времени . Здесь использовано следующее условие: текущий бит располагается в крайнем левом разряде, а крайние правые разрядов стартуют из состояния со всеми нулями. Этот момент времени обозначим как начальное время, . Время завершения последнего перехода обозначим как время прекращения работы, .