2.1. Тригонометрический ряд Фурье. Спектр периодического сигнала

2.2. Амплитудный и фазовый спектры периодической последовательности прямоугольных импульсов

2.3. Интегральное преобразование Фурье

2.4. Эффективная длительность и эффективная ширина спектра сигнала

2.5. Спектры неинтегрируемых сигналов

2.6. Корреляционно-спектральный анализ детерминированных сигналов

2.1. Тригонометрический ряд Фурье. Спектр периодического сигнала

Рассмотрение методов спектрального анализа радиотехнических сигналов мы начнем с детерминированных периодических сигналов. Как уже подчеркивалось выше детерминированные сигналы характеризуются тем, что в любой наперед заданный момент времени его значения можно точно определить. Периодическим детерминированным сигналом является сигнал известной формы периодически повторяющийся через интервал времени , называемый периодом повторения. Математически периодический сигнал описывается выражением

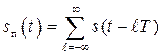, (2.1)

К периодическим сигналам относятся гармоническое колебание, определенное на бесконечном интервале времени, последовательность импульсов с известной амплитудой, длительностью и периодом повторения и другие.

Спектральный анализ предусматривает выбор системы базисных функций. На практике наибольшее распространение получили тригонометрические функции. Это обусловлено тем, что при преобразовании сигналов такой формы, например, линейными радиотехническими цепями их форма сохраняется, а меняются только амплитуда и фазы колебаний. С другой стороны, формирование таких сигналов осуществляется достаточно простыми техническими средствами.

Сигналы, описываемые тригонометрическими функциями, называются гармоническими сигналами, а спектральный анализ в системе базисных тригонометрических функций – гармоническим анализом.

Итак, выберем в качестве базисных функций систему

, (2.2)

где .

Нетрудно убедиться, что функции, образующие систему (2.2) являются ортогональными на интервале времени и удовлетворяют условию периодичности (2.1). Тогда в соответствии с (1.36) можно записать

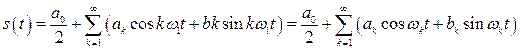, (2.3)

где .

Нормы базисных функций в соответствии с (1.26) равны

; .

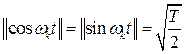Тогда из (1.39) вытекает

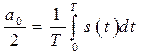, (2.4)

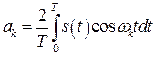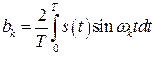, . (2.5)

Выражение (2.3) называется тригонометрическим рядом Фурье и представляет собой разложение сигнала на составляющие в системе тригонометрических функций.

В радиотехнической практике часто оказывается удобнее иное представление ряда (2.3). Выделим из (2.3) k-тую составляющую

и представим ее в виде

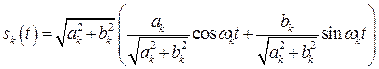, (2.6)

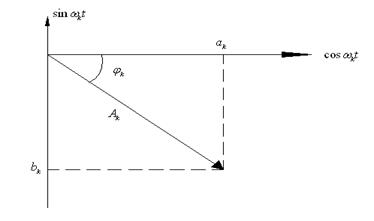
Рис. 2.1

С геометрической точки зрения составляющую можно рассматривать как вектор в системе координат (рис. 2.1). Длина вектора , а -угол, на который повернут вектор относительно оси . Нетрудно убедиться, что

, .

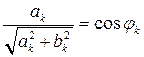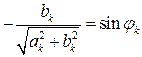Тогда выражение (2.6) принимает вид

, (2.7)

где .

С учетом (2.7), ряд Фурье (2.3) можно переписать следующим образом

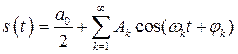. (2.8)

Составляющая

(2.9)

называется k-той гармонической составляющей или просто k-той гармоникой.

В соответствии с определением спектра, данном в предыдущем разделе, совокупность и составляют амплитудный спектр, а совокупность – фазовый спектр сигнала. Таким образом, амплитудный спектр периодического сигнала содержит постоянную составляющую и бесконечное число амплитуд соответствующих гармоник. То же самое относится и к фазовому спектру.

При спектральном анализе спектры удобно представлять в виде спектральных диаграмм.

На рис.2.2, а изображен периодический сигнал в координатах и . Проведем еще одну ось, перпендикулярную осям и и отложим на этой оси значения . Изобразим гармонические составляющие сигнала на этих частотах, а на оси частот отложим значения и в виде отрезков прямой. Если теперь развернуть всю систему координат вокруг оси на 90º в направлении стрелки, мы получим диаграмму амплитудного спектра сигнала (рис. 2.2, б). Таким же образом можно построить спектральную диаграмму фазового спектра, примерный вид которой показан на рис. 2.2, в.

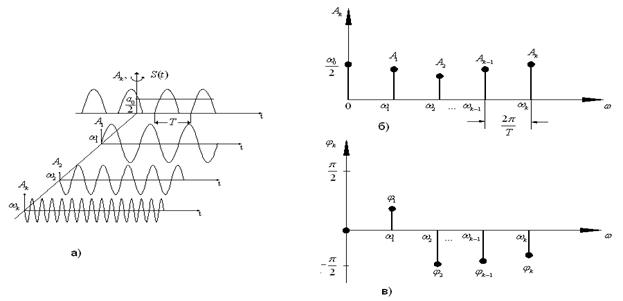
Рис. 2.2

2.2. Амплитудный и фазовый спектры периодической последовательности прямоугольных импульсов

В качестве примера приведем разложение в ряд Фурье периодической последовательности прямоугольных импульсов с амплитудой , длительностью и периодом следования , симметричной относительно нуля, т.е.

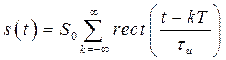, (2.10)

Здесь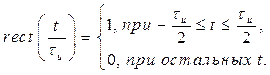

Разложение такого сигнала в ряд Фурье дает

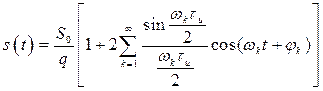, (2.11)

где – скважность.

Для упрощения записи можно ввести обозначение

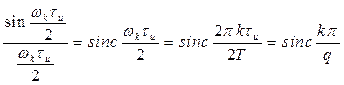, (2.12)

Тогда (2.11) запишется следующим образом

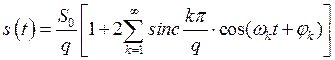, (2.13)

На рис. 2.3 изображена последовательность прямоугольных импульсов. Спектр последовательности, как впрочем, и любого другого периодического сигнала, носит дискретный (линейчатый) характер.

Огибающая спектра (рис. 2.3, б) пропорциональна . Расстояние по оси частот между двумя соседними составляющими спектра равно , а между двумя нулевыми значениями (ширина лепестка спектра) – . Число гармонических составляющих в пределах одного лепестка, включая правое по рисунку нулевое значение, составляет , где знак означает округление до ближайшего целого числа, меньшего (если скважность – дробное число), или (при целочисленном значении скважности). При увеличении периода основная частота уменьшается, спектральные составляющие на диаграмме сближаются, амплитуды гармоник также уменьшаются. При этом форма огибающей сохраняется.

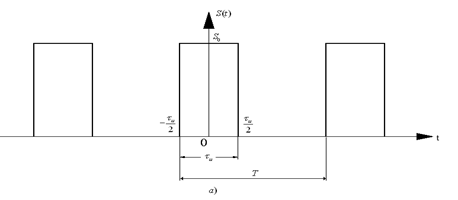
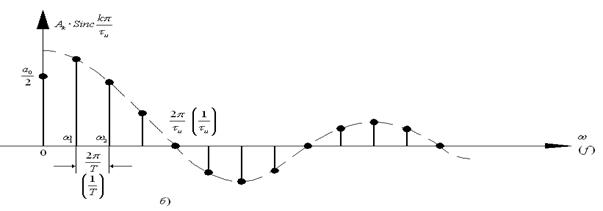
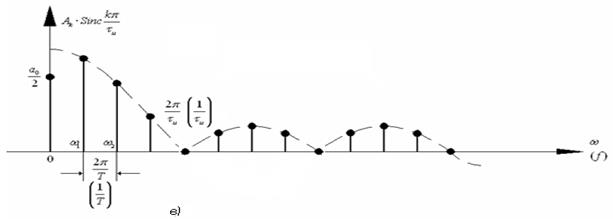
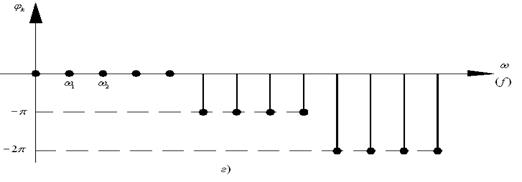
Рис. 2.3

При решении практических задач спектрального анализа вместо угловых частот используют циклические частоты , измеряемые в Герцах. Очевидно, расстояние между соседними гармониками на диаграмме составит , а ширина одного лепестка спектра – . Эти значения представлены на диаграмме в круглых скобках.

В практической радиотехнике в большинстве случаев вместо спектрального представления (рис. 2.3, б) используют спектральные диаграммы амплитудного и фазового спектров. Амплитудный спектр последовательности прямоугольных импульсов представлен на рис. 2.3, в.

Очевидно, огибающая амплитудного спектра пропорциональна .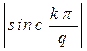

Что же касается фазового спектра (рис. 2.3, г), то полагают, что начальные фазы гармонических составляющих изменяются скачком на величину -π при изменение знака огибающей sinc kπ/q. Начальные фазы гармоник первого лепестка, полагаются равными нулю. Тогда начальные фазы гармоник второго лепестка составят φ = -π, третьего лепестка φ = -2π и т.д.

Рассмотрим еще одно представление сигнала рядом Фурье. Для этого воспользуемся формулой Эйлера

.

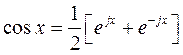В соответствии с этой формулой k-ю составляющую (2.9) разложения сигнала в ряд Фурье можно представить следующим образом

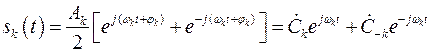, (2.14)

где

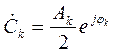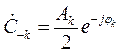; . (2.15)

Здесь величины и являются комплексными и представляют собой комплексные амплитуды составляющих спектра. Тогда ряд

Фурье (2.8) с учетом (2.14) примет следующую форму

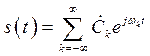, (2.16)

где

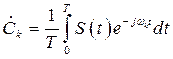, (2.17)

Нетрудно убедиться в том, что разложение (2.16) проводится по базисным функциям , которые также являются ортогональными на интервале , т.е.

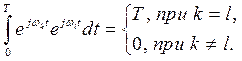
Выражение (2.16) представляет собой комплексную форму ряда Фурье, которая распространяется на отрицательные частоты. Величины и , где означает комплексную сопряженную с величину, называются комплексными амплитудами спектра. Т.к. является комплексной величиной, из (2.15) следует, что

и .

Тогда совокупность составляет амплитудный, а совокупность – фазовый спектр сигнала .

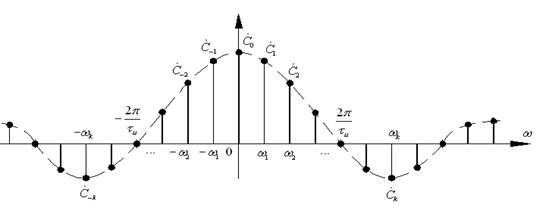
Рис. 2.4

На рис. 2.4 представлена спектральная диаграмма спектра рассмотренной выше последовательности прямоугольных импульсов, представленного комплексным рядом Фурье

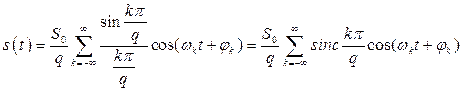
Спектр также носит линейчатый характер, но в отличие от ранее рассмотренных спектров определяется как в области положительных, так и в области отрицательных частот. Поскольку является чётной функцией аргумента , спектральная диаграмма симметрична относительно нуля.

Исходя из (2.15) можно установить соответствие между и коэффициентами и разложения (2.3). Так как

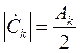и ,

то в результате получим

. (2.18)

Выражения (2.5) и (2.18) позволяют найти значения при практических расчетах.

Дадим геометрическую интерпретацию комплексной формы ряда Фурье. Выделим k-тую составляющую спектра сигнала. В комплексной форме k-я составляющая описывается формулой

, (2.19)

где и определятся выражениями (2.15).

В комплексной плоскости каждое из слагаемых в (2.19) изображается в виде векторов длиной , повернутых на угол и относительно вещественной оси и вращающихся в противоположных направлениях с частотой (рис. 2.5).

Очевидно, сумма этих векторов дает вектор, расположенный на вещественной оси, длина которого составляет . Но этот вектор соответствует гармонической составляющей

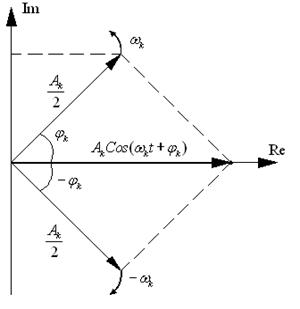
Рис. 2.5

Что касается проекций векторов на мнимую ось, то эти проекции имеют равную длину, но противоположные направления и в сумме дают ноль. А это значит, что сигналы, представленные в комплексной форме (2.16) в действительности являются вещественными сигналами. Иными словами, комплексная форма ряда Фурье является математической абстракцией, весьма удобной при решении целого ряда задач спектрального анализа. Поэтому, иногда спектр, определяемый тригонометрическим рядом Фурье, называют физическим спектром, а комплексной формой ряда Фурье – математическим спектром.

И в заключение рассмотрим вопрос распределения энергии и мощности в спектре периодического сигнала. Для этого воспользуемся равенством Парсеваля (1.42). При разложении сигнала в тригонометрический ряд Фурье выражение (1.42) принимает вид

.

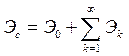Энергия постоянной составляющей

,

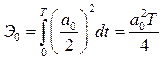а энергия k-той гармоники

.

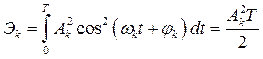Тогда энергия сигнала

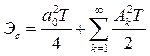. (2.20)

Т.к. средняя мощность сигнала

,

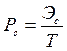то с учетом (2.18)

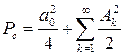. (2.21)

При разложение сигнала в комплексный ряд Фурье выражение (1.42) имеет вид

,

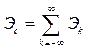где 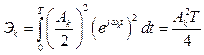- энергия k-той гармоники.

Энергия сигнала в этом случае

,

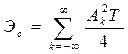а его средняя мощность

.

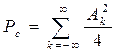Из приведенных выражений следует, что энергия или средняя мощность k-той спектральной составляющей математического спектра вдвое меньше энергии или мощности соответствующей спектральной составляющей физического спектра. Это обусловлено тем, что физического спектра распределяется поровну между и математического спектра.

Выражения (2.20) – (2.12) позволяют рассчитать и построить спектральные диаграммы распределения энергий или мощностей, т.е. энергетические спектры периодического сигнала.

2.3. Интегральное преобразование Фурье

Рассмотренный выше гармонический анализ периодических сигналов можно обобщить и на непериодические (одиночные) сигналы. Возвратимся к периодическому сигналу произвольной формы (рис. 2.6, а).

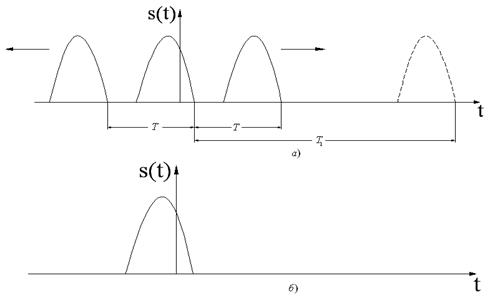
Рис. 2.6

Увеличим значение до . Соседние с центральным сигналы сдвинутся вправо и влево по оси времени. Если теперь устремить , на временной диаграмме (рис. 2.6, б) останется только одиночный сигнал конечной длительности. Если мощность сигнала отлична от нуля, то энергия такого сигнала конечна. Математически это условие равносильно требованию сходимости интеграла

,

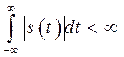где – абсолютное значение функции .

Иными словами функция должна быть абсолютно интегрируемой.

Обратимся к спектральным диаграммам (рис. 2.2, б, в). Т.к. расстояние по оси частот между соседними составляющими равно

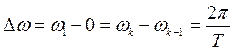, (2.24)

то с увеличением величина уменьшается и спектральные составляющие сближаются. При этом значения комплексных амплитуд составляющих уменьшаются. При величина и спектр из линейчатого становится сплошным и представляет собой бесконечно большое число гармоник и бесконечно малыми амплитудами.

Воспользуемся комплексной формой ряда Фурье (2.16). Подставляя в эту формулу выражение (2.17), получим

.

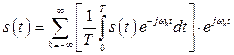Тогда с учетом того, что 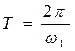и , запишем

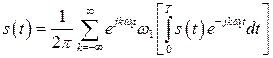. (2.25)

Т.к. в пределе при величина , то в соответствии с (2.24) превращается в бесконечно малое приращение , а частота k-той гармоники – в текущую частоту . При этом пределы внутреннего интеграла в (2.25) расширяются от до , а суммирование переходит в операцию интегрирования. С учетом этого выражение (2.25) принимает следующий вид:

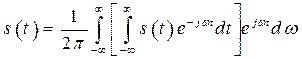. (2.26)

Интеграл, заключенный в скобки выражения (2.26), описывает комплексный спектр одиночного сигнала

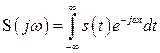. (2.27)

Тогда с учетом (2.27) выражение (2.26) запишется следующим образом

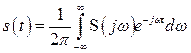. (2.28)

Выражения (2.27) и (2.28) представляют собой соответственно прямое и обратное преобразование Фурье.

Выясним физический смысл комплексного спектра одиночного сигнала. Зафиксируем некоторую частоту . Так как для периодического сигнала , то для вычисления комплексной амплитуды в выражении (2.17) пределы интегрирования можно распространить на область , т.е.

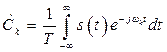. (2.29)

С другой стороны на этой же частоте для одиночного сигнала в соответствии с (2.27)

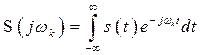. (2.30)

Так как интегралы в (2.29) и (2.30) совпадают, можно записать

, (2.31)

здесь период согласно (2.24) равен

,

где – элементарный интервал частот, измеряемый в герцах.

Тогда

.

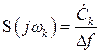В практической радиотехнике вместо комплексного спектра часто используют амплитудный спектр. В этом случае

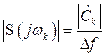. (2.32)

Отсюда следует, что характеризует плотность распределения амплитуд составляющих сплошного спектра одиночного сигнала по частоте. Если – изменяющиеся во времени напряжение или ток, то размерность составляет или .

Запишем (2.32) с учетом (2.24) в виде

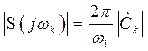. (2.33)

Отсюда следует, что огибающая сплошного спектра одиночного сигнала и огибающая соответствующего периодического сигнала совпадают по форме и отличаются только масштабом. На практике в ряде случаев при вычислении спектра периодического сигнала гораздо проще сначала найти одиночного сигнала, а затем, пользуясь соотношением (2.33) перейти к спектру периодического сигнала.

Преобразования Фурье (2.27) и (2.28) представлены в комплексной форме. Воспользовавшись известными соотношениями

, (2.34, а)

и

, (2.34,б)

можно получить тригонометрическую форму преобразований. Так, с учетом (2.34, б) выражение (2.27) принимает следующий вид

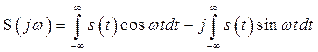, (2.35)

где первый интеграл представляет собой вещественную, а второй – мнимую часть , т.е.

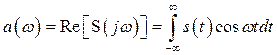, (2.36)

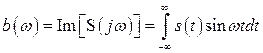. (2.37)

Тогда модуль или амплитудный спектр вычисляется по формуле

, (2.38)

а аргумент или фазовый спектр - в соответствии с выражением

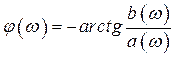. (2.39)

Если сигнал является четной функцией времени , то второй интеграл в (2.35) равен нулю, т.к. произведение является нечетной функцией, а пределы интегрирования симметричны относительно нуля. В этом случае описывается вещественной и четной функцией

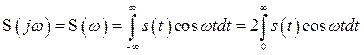. (2.40)

Если же сигнал является нечетной функцией времени, то первый интеграл обращается в ноль и представляет собой нечетную и чисто мнимую функцию частоты , т.е.

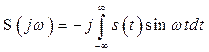. (2.41)

Таким образом (2.35), (2.40) и (2.41) характеризуют тригонометрическую форму прямого преобразования Фурье.

Обратимся теперь к обратному преобразованию Фурье (2.28).

С учетом того, что

,

выражение (2.28) можно представить в следующем виде

,

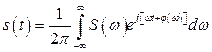или, в соответствии с (2.34,а)

.

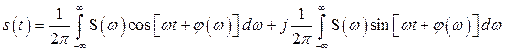Если – четная функция, то второй интеграл является нечетной функцией и его значение равно нулю. Тогда окончательно запишем

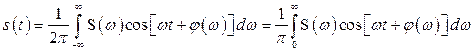. (2.42)

В качестве примера рассмотрим преобразование Фурье прямоугольного импульса длительности и амплитудой , определенного на интервале

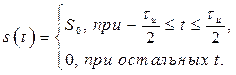
Воспользовавшись выражением (2.27), после несложных преобразований получим

.

На рис. 2.7 изображены форма импульса и его спектральная функция.

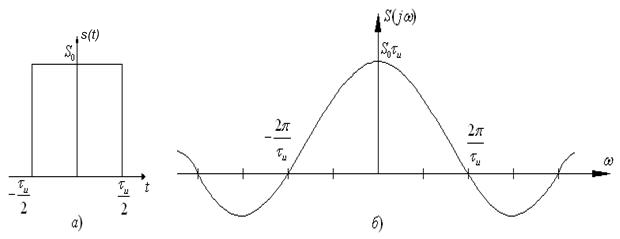
Рис. 2.7

Сравнение спектральных диаграмм рис. 2.4 и рис. 2.7,б показывает, что формы огибающей линейчатого и сплошного спектров совпадают, что подтверждает сделанные ранее выводы. При этом как огибающая линейчатого, так и огибающая сплошного спектров достигают нулевого значения на частотах ω = 2lπ/τ, где . При значение спектральной функции равно площади импульса.

Перейдем к рассмотрению основных свойств преобразования Фурье. Для краткости записи пару преобразований (прямое и обратное) символически будем представлять следующим образом:

1. Линейность преобразования Фурье

, (2.43)

где и – произвольные числовые коэффициенты.

Доказательство формулы (2.43) не вызывает затруднений, для этого достаточно подставить сумму в выражение (2.27).

2. Свойство временного сдвига (теорема запаздывания)

. (2.44)

Т.к. , то (2.44) можно представить в виде

. (2.45)

Таким образом задержка сигнала во времени на величину приводит к изменению его фазового спектра на .

3. Изменение масштаба времени

. (2.46)

В зависимости от величины имеет место либо сжатие , либо растяжение сигнала во времени. Из (2.46) следует, что при сжатии сигнала во времени в раз происходит расширение его спектра во столько же раз. И наоборот.

4. Операция дифференцирования

. 2.47)

При дифференцировании сигнала все гармонические составляющие его спектра изменяют начальную фазу на .

5. Операция интегрирования

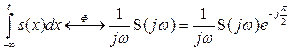. (2.48)

При интегрировании сигнала все гармонические составляющие его спектра изменяют начальную фазу на . Свойство (2.48) справедливо, если

.

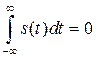6. Если , то

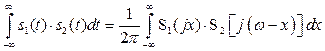. (2.49)

Интеграл в правой части выражения (2.49) называется сверткой. Таким образом, преобразование Фурье произведения сигналов представляет собой свертку (с коэффициентом ) их спектров. В частном случае при и равенстве двух сигналов можно получить следующее соотношение:

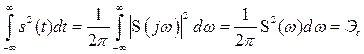, (2.50)

которое представляет собой интегральную форму равенства Парсеваля (2.22). Из этого соотношения следует, что полная энергия непериодического сигнала равна сумме энергий всех его спектральных составляющих. При этом зависимость

, (2.51)

представляет собой спектральную плотность энергии или энергетический спектр одиночного сигнала.

2.4. Эффективная длительность и эффективная ширина спектра сигнала

Для решения практических задач радиотехники крайне важно знать значения длительности и ширины спектра сигнала, а также соотношение между ними. Знание длительности сигнала позволяет решать задачи эффективного использования времени, предоставляемого для передачи сообщений, а знание ширины спектра – эффективного использования диапазона радиочастот.

Решение указанных задач требует строгого определения понятий «эффективная длительность» и «эффективная ширина спектра». На практике существует большое число подходов к определению длительности. В том случае, когда сигнал ограничен во времени (финишный сигнал), как это имеет место, например, для прямоугольного импульса, определение длительности не встречает затруднений. Иначе обстоит дело, когда теоретически сигнал имеет бесконечную длительность, например, экспоненциальный импульс

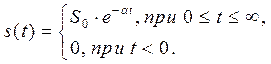
В этом случае в качестве эффективной длительности может быть принят интервал времени , в течение которого значение сигнала . При другом способе в качестве выбирают интервал времени, в течение которого . То же самое можно сказать и в отношении определения эффективной ширины спектра .

Хотя в дальнейшем, некоторые из этих способов будут использоваться при анализе радиотехнических сигналов и цепей, следует отметить, что выбор способа существенно зависит от формы сигнала и структуры спектра. Так для экспоненциального импульса более предпочтителен первый из указанных способов, а для сигнала колоколообразной формы – второй способ.

Более универсальным является подход, использующий энергетические критерии. При таком подходе в качестве эффективной длительности и эффективной ширины спектра рассматриваются соответственно интервал времени и диапазон частот, в пределах которых сосредоточена подавляющая часть энергии сигнала

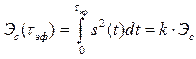, (2.52)

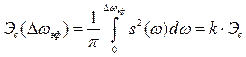, (2.53)

где – коэффициент, показывающий, какая часть энергии сосредоточена в интервалах или . Обычно величину выбирают в пределах .

Применим критерии (2.52) и (2.53) для определения длительности и ширины спектра прямоугольного и экспоненциального импульсов. Для прямоугольного импульса вся энергия сосредоточена в интервале времени или , поэтому его длительность . Что касается эффективной ширины спектра, то установлено, что более 90% энергии импульса сосредоточено в пределах первого лепестка спектра. Если рассматривать односторонний (физический) спектр импульса, то ширина первого лепестка спектра составляет в круговых частотах или в циклических частотах. Отсюда следует, что эффективная ширина спектра прямоугольного импульса равна

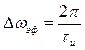или .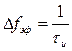

Перейдем к определению и экспоненциального импульса. Полная энергия импульса составляет

.

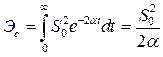Воспользовавшись (2.52), получим

.

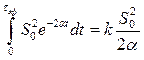Вычислив интеграл в левой части уравнения и решив его, можно прийти к следующему результату

.

Спектр экспоненциального импульса найдем, воспользовавшись преобразованием Фурье

,

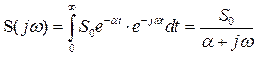откуда следует

.

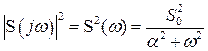Подставляя это выражение в (2.53) и решая уравнение, получим

.

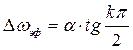Найдем произведение эффективной длительности на эффективную ширину спектра. Для прямоугольного импульса это произведение составляет

,

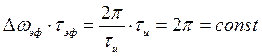или для циклических частот

.

Для экспоненциального импульса

.

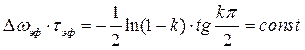Таким образом, произведение эффективной длительности на эффективную ширину спектра одиночного сигнала есть постоянная величина, зависящая только от формы сигнала и величины коэффициента . Это означает, что при уменьшении длительности сигнала его спектр расширяется и наоборот. Этот факт уже отмечался пи рассмотрении свойства (2.46) преобразования Фурье. На практике это означает, что невозможно сформировать короткий сигнал, обладающий узким спектром, что является проявлением физического принципа неопределенности.

2.5. Спектры неинтегрируемых сигналов

Одним из условий применимости преобразования Фурье функции , описывающей форму сигнала, является ее абсолютная интегрируемость, что означает конечную энергию сигнала. Вместе с тем в ряде случаев спектрально удовлетворяющих этому условию. Это может быть гармоническое колебание, используемое в качестве несущего колебания при осуществлении операции модуляции, сигналы, описываемые единичной функцией и др. Однако, и на эти сигналы может быть распространен аппарат преобразования Фурье.

Рассмотрим сначала сигнал вида

.

Очевидно такой сигнал обладает бесконечной энергией. Применим формально к этому сигналу преобразование Фурье (2.27)

.

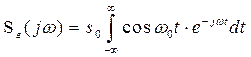Так как

,

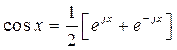то (2.54) можно переписать следующим образом

.

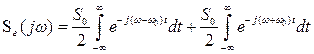Воспользовавшись табличным интегралом

,

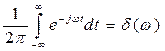где – рассмотренная выше - функция.

Тогда, с учетом этого выражения, получим

.

Из (2.55) следует, что спектр гармонического колебания определенного на интервале времени , равен нулю на всех частотах, кроме и . На этих частотах значение спектральных составляющих обращается в бесконечность (рис. 2.8, а)

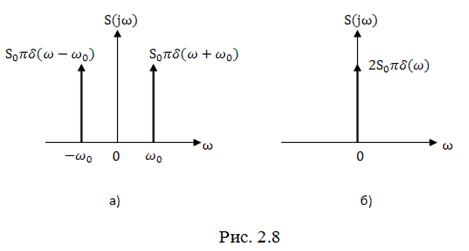
Если положить , что соответствует постоянному сигналу , то из (2.55) следует

.

Таким образом, спектр постоянного сигнала отличен от нуля только при (рис. 2.8,б). На этой частоте значение спектральной составляющей равно бесконечности.

Можно показать [Л.3], что спектр ступенчатого сигнала

,

равен

.

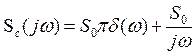Из выше изложенного следует, что спектры неинтегрируемых сигналов можно вычислить, используя преобразование Фурье с привлечением математической абстракции – - функции. Тогда возникает вопрос: а что же представляет собой спектр сигнала, форма которого описывается - функцией, т.е.

.

Применяя (2.27) к этому сигналу и учитывая фильтрующее свойство -функции, получим

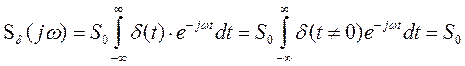. (2.56)

Следовательно сигнал, представляющий собой произведение на - функцию (на практике – очень короткий импульс очень большой амплитуды) имеет равномерный спектр по всему диапазону частот. Этот важный для радиотехнических задач вывод будет использован в дальнейшем.

2.6. Корреляционно-спектральный анализ детерминированных сигналов

Во многих радиотехнических задачах часто возникает необходимость сравнения сигнала и его копии, сдвинутой на некоторое время . В частности такая ситуация имеет место в радиолокации, где отраженный от цели импульс поступает на вход приемника с задержкой во времени. Сравнение этих сигналов между собой, т.е. установление их взаимосвязи, при обработке позволяет определять параметры движения цели.

Для количественной оценки взаимосвязи сигнала и его сдвинутой во времени копии вводится характеристика

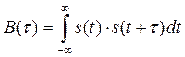, (2.57)

Которая называется автокорреляционной функцией (АКФ).

Для пояснения физического смысла АКФ приведем пример, где в качестве сигнала выступает прямоугольный импульс длительностью и амплитудой . На рис. 2.9 изображены импульс, его копия, сдвинутая на интервал времени и произведение . Очевидно, интегрирование произведения дает значение площади импульса, являющегося произведением . Это значение при фиксированном можно изобразить точкой в координатах . При изменении мы получим график автокорреляционной функции.

Найдем аналитическое выражение . Так как

то подставляя это выражение в (2.57), получим

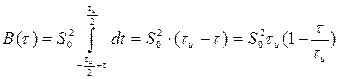. (2.58)

Если осуществлять сдвижку сигнала влево, то аналогичными вычислениями нетрудно показать, что

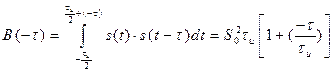. (2.59)

Тогда объединяя (2.58) и (2.59), получим

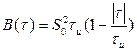. (2.60)

Из рассмотренного примера можно сделать следующие важные выводы, распространяющиеся на сигналы произвольной формы:

1.                Автокорреляционная функция непериодического сигнала с ростом убывает (необязательно монотонно для других видов сигналов). Очевидно, при АКФ также стремиться к нулю.

2.                Своего максимального значения АКФ достигает при . При этом, равна энергии сигнала. Таким образом, АКФ является энергетической характеристикой сигнала. Как и следовало ожидать при сигнал и его копия полностью коррелированны (взаимосвязаны).

3.                Из сравнения (2.58) и (2.59) следует, что АКФ является четной функцией аргумента , т.е.

.

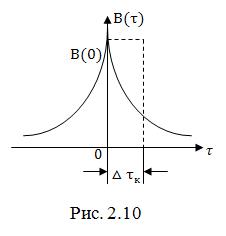
Важной характеристикой сигнала является интервал корреляции. Под интервалом корреляции понимают интервал времени , при сдвижке на который сигнал и его копия становятся некоррелированными.

Математически интервал корреляции определяется следующим выражением

,

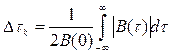или поскольку – четная функция

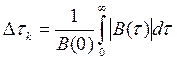. (2.61)

На рис. 2.10 изображена АКФ сигнала произвольной формы. Если построить прямоугольник, по площади равный площади под кривой при положительных значениях (правая ветвь кривой), одна сторона которого равна , то вторая сторона будет соответствовать .

Найдем интервал корреляции для прямоугольного импульса. Подставляя (2.58) в (2.60) после несложных преобразований, получим:

,

что и следует из рис. 2.9.

По аналогии с автокорреляционной функцией степень взаимосвязи двух сигналов и оценивается взаимной корреляционной функцией (ВКФ)

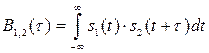. (2.62)

Найдем взаимную корреляционную функцию двух сигналов: прямоугольного импульса с амплитудой и длительностью

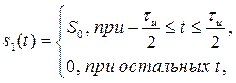
и треугольного импульса той же амплитуды и длительности

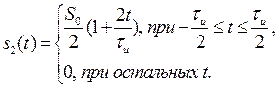
Воспользовавшись (2.61) и вычисляя интегралы отдельно для и , получим:

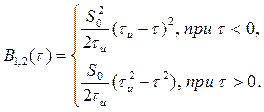
Графические построения, иллюстрирующие вычисления ВКФ, приведены на рис. 2.11

Здесь пунктирными линиями показано исходное (при ) положение треугольного импульса.

При выражение (2.61) преобразуется в (2.57). Отсюда следует, что АКФ является частным случаем ВКФ при полностью совпадающих сигналах.

Отметим основные свойства ВКФ.

1. Так же, как и автокорреляционная функция, ВКФ является убывающей функцией аргумента . При ВКФ стремиться к нулю.

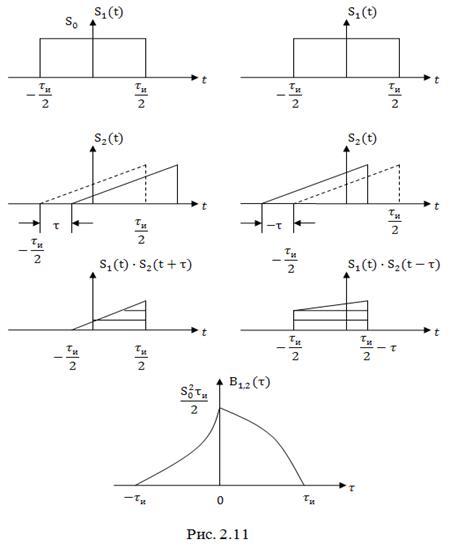
2. Значения взаимной корреляционной функции при произвольных представляют собой значения взаимной энергии (энергии взаимодействия) сигналов и .

3. При взаимная корреляционная функция (в отличие от автокорреляционной) не всегда достигает максимума.

4. Если сигналы и описываются четными функциями времени, то ВКФ тоже четна. Если же хотя бы один из сигналов описывается нечетной функцией, то ВКФ так же нечетна. Первое утверждение легко доказать, если вычислить ВКФ двух прямоугольных импульсов противоположной полярност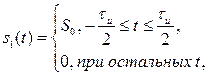и

и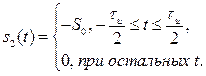

Взаимная корреляционная функция таких сигналов

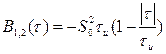, (2.63)

является четной функцией аргумента .

Что же касается второго утверждения рассмотренный пример вычисления ВКФ прямоугольного и треугольного импульсов доказывает его.

В некоторых прикладных задачах радиотехники используют нормированную АКФ

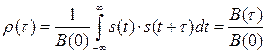, (2.64)

и нормированную ВКФ

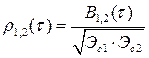, (2.65)

где и – собственные энергии сигналов и . При значение нормированной ВКФ называют коэффициентом взаимной корреляции. Если , то коэффициент взаимной корреляции

.

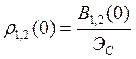Очевидно, значения лежат в пределах от -1 до +1. Если сравнить (2.65) с (1.32), то можно убедиться, что коэффициент взаимной корреляции соответствует значению косинуса угла между векторами и при геометрическом представлении сигналов.

Рассчитаем коэффициент взаимной корреляции для рассмотренных выше примеров. Так как энергия сигнала прямоугольного импульса составляет

,

а треугольного импульса

,

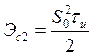то коэффициент взаимной корреляции в соответствии с (2.62) и (2.65) будет равен . Что же касается второго примера, то для двух прямоугольных импульсов одинаковой амплитуды и длительности, но противоположной полярности, .

Экспериментально АКФ и ВКФ могут быть получены с помощью устройства, структурная схема которого изображена на рис. 2.12

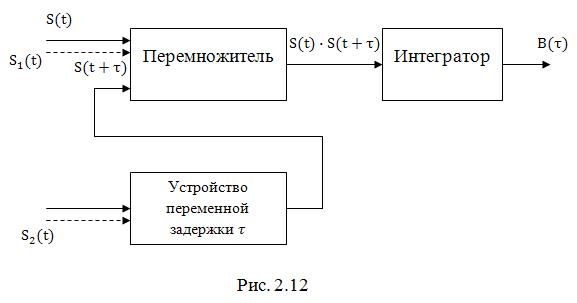
При снятии АКФ на один из входов перемножителя поступает сигнал , а на второй – этот же сигнал, но задержанный на время . Сигнал, пропорциональный произведению , подвергается операции интегрирования. На выходе интегратора формируется напряжение, пропорциональное значению АКФ при фиксированном . Изменяя время задержки, можно построить АКФ сигнала.

Для экспериментального построения ВКФ сигнал подается на один из входов перемножителя, а сигнал – на устройство задержки (входящие цепи показаны пунктиром). В остальном, устройство работает аналогичным образом. Отметим, что описанное устройство называется коррелятором и широко используется в различных радиотехнических системах для приема и обработки сигналов.

До сих пор мы проводили корреляционный анализ непериодических сигналов, обладающих конечной энергией. Вместе с тем, необходимость подобного анализа часто возникает и для периодических сигналов, которые теоретически обладают бесконечной энергией, но конечной средней мощностью. В этом случае АКФ и ВКФ вычисляются усреднением по периоду и имеют смысл средней мощности (собственной или взаимной соответственно). Таким образом, АКФ периодического сигнала:

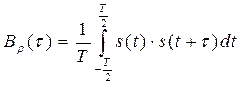, (2.66)

а взаимная корреляционная функция двух периодических сигналов с кратными периодами:

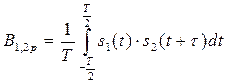, (2.67)

где – наибольшее значение периода.

Найдем автокорреляционную функцию гармонического сигнала

,

где 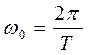– круговая частота, – начальная фаза.

Подставляя это выражение в (2.66) и вычисляя интеграл с использованием известного тригонометрического соотношения:

,

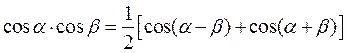получим:

.

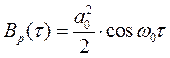Из рассмотренного примера можно сделать следующие выводы, справедливые для любого периодического сигнала.

1. АКФ периодического сигнала является периодической функцией с тем же периодом.

2. АКФ периодического сигнала является четной функцией аргумента .

3. При значение представляет собой среднюю мощность, которая выделяется на сопротивлении в 1 Ом и имеет размеренность .

4. АКФ периодического сигнала не содержит информации о начальной фазе сигнала.

Следует также отметить, что интервал корреляции периодического сигнала .

А теперь вычислим взаимную корреляционную функцию двух гармонических сигналов одинаковой частоты, но отличающихся амплитудами и начальными фазами

и .

Воспользовавшись (2.67) и проводя несложные вычисления, получим

,

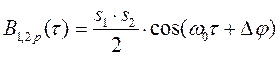где – разность начальных фаз сигналов и .

Таким образом, взаимная корреляционная функция двух рассматриваемых сигналов содержит информацию о разности начальных фаз. Это важное свойство широко используется при построении различных радиотехнических устройств, в частности, устройств синхронизации некоторых систем радиоавтоматики и других.

В заключение установим связь между АКФ непериодического сигнала и его энергетическим спектром, определение которого [см. (2.51)] было дано выше. Для этого воспользуемся (2.49) при . Тогда получим соотношение

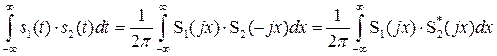, (2.68)

где – функция, комплексно сопряженная с .

Положим теперь и . В соответствии с (2.45) преобразование Фурье имеет вид

.

С другой стороны

.

Подставляя эти выражения в (2.68), получим

.

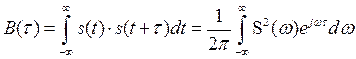Но в соответствие с (2.51) есть энергетический спектр. Тогда окончательно

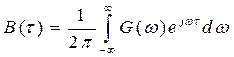. (2.69)

Применяя к прямое преобразование Фурье, приходим к соотношению

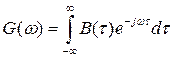. (2.70)

Таким образом, АКФ и энергетический спектр сигнала связаны парой преобразований Фурье.

Так как и – вещественные и четные функции, выражения (2.69) и (2.70) можно записать соответственно в виде

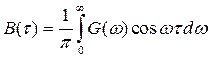, (2.71)

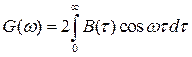. (2.72)

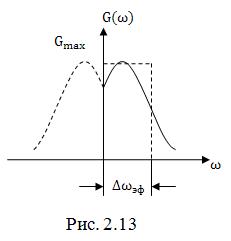
Рассмотренный корреляционно-спектральный анализ позволяет дать еще одну трактовку эффективной ширины спектра. Если известен энергетический спектр, то эффективная ширина спектра определяется так:

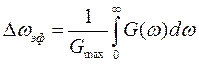. (2.73)

Иными словами представляет собой сторону прямоугольника по площади равного площади под кривой одностороннего спектра, вторая сторона которого равна (рис.2.13). Очевидно, произведение эффективной ширины энергетического спектра на величину интервала корреляции есть величина постоянная

.

Таким образом, и в этом случае мы сталкиваемся с проявлением принципа неопределенности: чем больше интервал корреляции, тем меньше ширина энергетического спектра, и наоборот.