8.1. Энергетические уровни

8.2. Квантовые переходы

8.3. Ширина спектральной линии

8.4. Возможность усиления и генерации в квантовых системах

8.5. Взаимодействие бегущих электромагнитных волн с активной средой

8.1. Энергетические уровни

Квантовая система, состоящая из микрочастиц, электронов, ядер, атомов и так далее, отличаются тем, что ее внутренняя энергия может принимать только дискретные значения. Возможные дискретные значения энергии называют энергетическими уровнями.

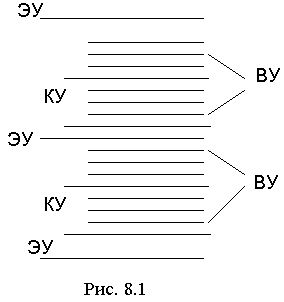
В свободных атомах квантуется энергия электронов и имеется система энергетических уровней электронов. Наблюдаются следующие движения частиц: движение электронов в атоме, колебания атомов в молекуле, вращение и поступательное движение молекул. Квантование энергии приводит к образованию сложной системы энергетических уровней. Основной системой являются электронные уровни ЭУ, отстоящие друг друга на 1 – 10 эВ. Между электронными уровнями располагаются колебательные уровни КУ с расстоянием примерно 0,1 эВ, а между колебательными уровнями находятся вращательные уровни ВУ с интервалом 10ֿ³ эВ и менее.

Переходы между электронными уровнями соответствуют излучению в видимом и ультрафиолетовом диапазонах, между колебательными уровнями - инфракрасному, а между вращательными - СВЧ диапазону.

В твёрдых телах взаимодействие частиц становится настолько сильным, что образуются зоны с очень близко расположенными уровнями, между этими зонами имеются зоны запрещённых значений энергии (запрещённые зоны).

В атомах осуществляются только те переходы между энергетическими уровнями, которые удовлетворяют правилам отбора, устанавливающим допустимые различия квантовых чисел. Переходы, удовлетворяющие правила отбора, называются разрешёнными, а остальные - запрещёнными. Переходы с излучением или поглощением квантов электромагнитной энергии (фотонов) называют излучательными, а переходы, в которых квант энергии выделяется в виде тепла в среде,- безызлучательными. Состояние, из которого запрещены все излучательные переходы в более низкие энергитические состояния, называется метастабильными.

8.2. Квантовые переходы

Спонтанные переходы – самопроизвольные квантовые переходы из верхнего энергетического состояния в нижнее. Уровень, соответствующий наименьшей возможной энергии, называется основным, а остальные – возбуждёнными. Частота излучения определяется из постулата Бора

,

где энергия верхнего (ε_j ) и нижнего (ε_i ) уровней; h- постоянная Планка. Частота называется частотой квантового перехода. Число частиц с одинаковой энергией в единице объёма называется населённостью уровня. Пусть номер верхнего уровня j=2, а нижнего i=1. Обозначим населённости этих уровней N2 и N1. При спонтанных переходах происходят изменение населённости уровней, уменьшение верхнего 2 и увеличение нижнего 1.

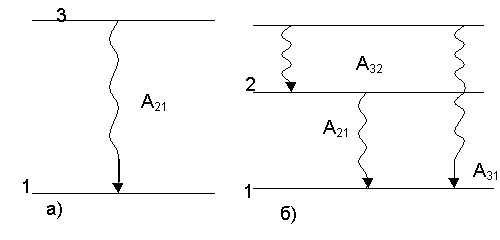
Рис. 8.2

Уменьшение населённости уровня 2 в результате только спонтанных переходов за время dt пропорционально населённости этого уровня N2 и времени dt: dN₂= -A₂₁N₂dt, где A_{21_}- коэффициент Эйнштейна для спонтанных переходов, определяющий вероятность спонтанного перехода в 1 с. Решив, получить экспоненциальный закон уменьшения населённости уровня 2 во времени:

N₂(t)=N₂(0)exp(­A₂₁t),

где N₂(0) – населённость в момент времени t = 0.

Насколько уменьшится населённость N₂ настолько же возрастёт населённость N₁ так как общее число частиц в объёме остаётся неизменным. Из этого следует, что через время t=1/A21 населённость N2 уменьшится в е = 2,718 раза по сравнению с начальным значением N2(0). Величина τ²=1/A21 характеризует время жизни в возбуждённом состоянии 2 и называется временем жизни на уровне. Коэффициент Эйнштейна объёма в 1с, или среднее число частиц, совершивших самопроизвольный переход из верхнего состояния в нижнее, т. е. имеет размерность и может быть любым, в отличии от математической вероятности, меняющейся от 0 до 1.

За 1 с в единице объёма число спонтанных переходов

N₂₁(c)=A₂₁N₂.

При каждом спонтанном переходе частицы выделяется квант энергии, поэтому за 1 с с учётом излучается энергия

P₂₁(c)=n₂₁(c)hν₂₁=A₂₁N₂hν₂₁.

Случайность спонтанных переходов означает, что различные частицы излучают неодновременно и независимо, т. е., фазы электромагнитных волн, излучаемых отдельными частицами, не согласованы друг с другом. Излучение обычных источников света есть результат спонтанных переходов.

В системе частиц, имеющих несколько энергетических уровней возможны спонтанные переходы частиц с данного уровня на нижние. Полная вероятность А_ј спонтанного перехода с уровня ј на все нижние уровни ί πавна сумме вероятностей отдельных переходов А јί:

A _ј= Σ A _јі = A _ј1+A_ј2+...+A _ј(ј-1).

Уровни, для которых вероятность спонтанных переходов очень мала, называют метастабильными.

Время жизни на уровне j в многоуровневой системе определяется аналогично с учётом.

τ _j=1/A _j.

Вынужденные переходы – это квантовые переходы частиц под действием внешнего электромагнитного поля, частота которого совпадает или близка к частоте перехода. При этом возможны переходы с верхнего уровня 2 на нижний 1 и с нижнего на верхний. В первом случае под действием внешнего электромагнитного поля с частотой ν₂₁ происходит вынужденное испускание кванта энергии hν₂₁. Особенность вынужденного испускания состоит в том, что появившийся фотон полностью идентичен фотону внешнего поля. Вынужденное излучение имеет такие же частоту, фазу, направление распространения и поляризацию, как и вынуждающее излучение. Поэтому вынужденное излучение увеличивает энергию электромагнитного поля с частотой перехода ν₂₁. Это служит предпосылкой для создания квантовых усилителей и генераторов.

В противоположность этому для перевода частицы из нижнего энергетического состояния 1 в верхнее 2 необходимо затратить энергию внешнего поля, равную разности энергии верхнего и нижнего уровней.

Таким образом, при каждом вынужденном переходе снизу вверх затрачивается квант энергии внешнего поля hν₂₁.

Вынужденные переходы, так же как и спонтанные, имеют статистический характер. Поэтому вводится вероятностные коэффициенты: W₂₁ - вероятность вынужденного перехода сверху вниз и W₁₂ - снизу вверх в 1с. Эти вероятности определяются соотношениями,

W₂₁=B₂₁u_ν, W₁₂=B₁₂u_ν,

где В₂₁ и В₁₂ - коэффициенты Эйнштейна для вынужденных переходов с излучением и поглощением энергии соответственно.

Число вынужденных переходов сверху вниз с излучением энергии в единицу времени в единицу объёма пропорционально вероятности W₂₁ и населённости верхнего уровня N₂.

n₂₁(в)=W₂₁N2=B₂₁u_νN₂.

Аналогично при тех же условиях число вынужденных переходов снизу вверх с поглощением энергии:

n₁₂(в)=W₁₂N₁=B₁₂u_νN₁

Соотношение между коэффициентами Эйнштейна.

Связь между коэффициентами Эйнштейна А₂₁, В₂₁ и В₂₁ можно установить, предполагая, что внутри полости, представляющей абсолютно чёрное тело, находится система атомов при температуре Т.

Пусть система атомов имеет два уровня энергии ε₂ и ε₁ , при переходах между которыми излучается или поглощается квант энергии hν₂₁. При термодинамическом равновесии в системе не происходит изменения энергии, поэтому число излучённых квантов должно быть равно числу поглощённых.

Следовательно, в единицу времени во всей системе общее число переходов из верхнего энергетического состояния в нижнее должно быть равно общему числу переходов из нижнего в верхнее:

n₂₁=n₁₂.

В состоянии равновесия в системе имеется равновесная плотность поля излучения u_ν, которая определяет число вынужденных переходов в системе.

Полное число переходов сверху вниз n₂₁в состоянии равновесия определяется суммой числа спонтанных переходов n₂₁(с) и вынужденных переходов с излучением энергии n₂₁(в),

n₂₁=n₂₁(с)+n₂₁(в)=(A₂₁+B₂₁u_ν)N₂.

Число переходов n₁₂ снизу вверх определяется только вынужденными переходами с поглощением.

n₁₂=n₁₂(в)=B₁₂uνN₁.

Приравнивая на основании n₂₁ и n₁₂ получаем

B₁₂u_νΝ₁=(A₂₁+B₂₁u_ν)N₂

Из этого найдём равновесную плотность энергии поля

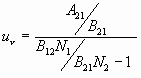
Соотношение населенностей уровней в состоянии термодинамического равновесия определяется законом Больцмана.

N₂б/N₁б=(g₂/g₁)exp[-(ε₂-ε₁)/κΤ],

где g₁ и g₂ -статистический вес уровней; κ - постоянная Больцмана; Т- абсолютная температура.

Для невырожденных уровней (g¹=g²=1) закон Больцмана принимает более простую форму записи

N₂б/N₁б=exp[-(ε₂-ε₁)/κΤ],

которая будет далее использоваться. Учитывая, что ε₂ - ε_{1 =} hν₂₁, получаем

Эйнштейн постулировал, что равновесная спектральная плотность энергии поля должна быть равна её значению, рассчитанному по формуле Планка для равновесного излучения абсолютно чёрного тела:

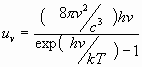
если вместо hν подставить hν₂₁.

Сравнивая с учётом этого, получаем условия тождественности этих формул:

B₁₂=B₂₁,

A₂₁=(8πhν³₂₁/c³)B₂₁.

Таким образом, если квантовая система и поле излучения находятся в состоянии термодинамического равновесия, то вероятности вынужденных переходов в единицу времени при единичной плотности полей В₁₂и В₂₁ должны быть одинаковы. Вероятность спонтанных переходов пропорциональна третьей степени частоты перехода, поэтому спонтанное излучение сильнее всего проявляется в оптическом диапазоне волн.

Безызлучательные переходы. Атомы и молекулы газа в результате неупругих соударений друг с другом или с электронами теряют или приобретают энергию. При этом энергия электромагнитного поля не излучается, не поглощается. Такие энергетические переходы принято называть безызлучательными. В твёрдом теле безызлучательные переходы происходят вследствие колебательного движения кристаллической решетки.

Безызлучательные переходы характеризуются также вероятностью перехода между уровнями j и i сверху вниз ωјі и снизу вверх ωіј соответственно с потерей и получением порции энергии

В соответствии с принципами детального равновесия в состоянии термодинамического равновесия подобно число безызлучательных переходов с уровня ј на уровень і в 1 с равно числу обратных безызлучательных переходов с уровня і на уровень ј:

ω_јіΝ_ј=ω_іјΝ_і.

В состоянии термодинамического равновесия распределение населённостей определяется законом Больцмана.

ω_јі/ω_іј = exp (hν_јі/κΤ),

Из чего следует, что вероятность безызлучательных переходов сверху вниз больше, чем снизу вверх, т.е. ω_јі>ω_іј ј>і, в отличие от вероятностей вынужденных переходов, которые одинаковы ( W_ji = W_ij). Если hν_јі<<κΤ, что обычно справедливо для квантовых приборов СВЧ диапазона, то можно заменить выражением

ω_јі/ω_іј=1+hν_јі/κΤ.

Релаксационные переходы. Изолированная система, в которой распределение частиц по энергии отличается от равновесного, называется неравновесной. Неравновесное состояние наблюдается при внешнем воздействии, после прекращения которого система возвращается в равновесное состояние. Процесс установления равновесия в системе называется релаксацией, а переходы частиц с одного уровня на другой в процессе релаксации - релаксационными переходами. В основе процесса релаксации лежит взаимодействие частиц (электронов, атомов, молекул, ионов) между собой и со стенками объёма. Рассмотренные безызлучательные переходы являются релаксационными. К релаксационным переходам следует отнести и спонтанные, роль которых в оптическом диапазоне. Рекласационные переходы приходится учитывать при рассмотрении процессов, выводящих систему из равновесного состояния. При постоянном внешнем воздействии возможна компенсация релаксационных процессов, тогда система будет находится в стационарном неравновесном состоянии. Релаксационные переходы влияют также на ширину спектральной линии.

8.3. Ширина спектральной линии

Естественная ширина спектральной линии. До сих пор предполагалось, что энергетические уровни бесконечно узкие. Однако даже в идеализированном случае, когда на частицу не действуют внешние силы, ширина энергетических уровней кончена. Другими словами, изучение для данного перехода не монохроматическое, а имеет некоторый спектр частот. Зависимость интенсивности излучения от частоты называют спектральной линией излучения, а графическое изображение её – контуром спектральной линии.

Минимальная ширина уровней, а, следовательно, и минимальная ширина спектральной линии определяется соотношением неопределённостей Гейзенберга, которое в данном случае лучше записать в виде

∆ε ∆t≥h

где ∆ε и ∆t - неопределённости энергии и времени.

Предположим, что необходимо определить частоту излучения при переходе с уровня 2 на основной уровень 1. Время жизни частиц в возбуждённом состоянии определяется τ₂=1/A₂₁. Следует считать, что неопределённость времени равна времени жизни частиц, т.е. Δt=τ₂. Подставляя Δt, получаем неопределённость энергии уровня 2 Δε₂>h/τ₂. Неопределённость энергии любого уровня j

Δ ε_ј>h/τ_ј,

где τ_ј – время жизни частицы на уровне ј, определяемое по вероятностям спонтанных переходов с него на нижние уровни.

Соотношение определяет зависимость ширины любого энергетического уровня от среднего времени жизни частиц на этом уровне. Если последнее бесконечно велико, то неопределённость энергии, или ширина уровня, бесконечно мала.

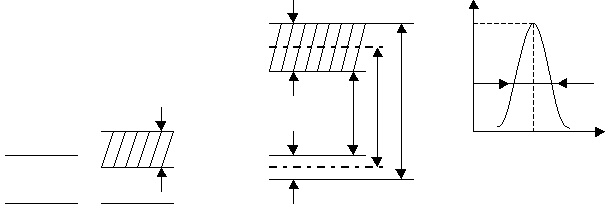
Рис. 8.3

Такими будут основной энергетический уровень, нижний уровень системы. Наиболее широкими оказываются уровни с малым временем жизни. Неопределённость частоты перехода между “размытыми” уровнями и с ширинами и находятся из соотношения и определяется суммой неопределённостей энергии обоих уровней. Ширина спектральной линии изолированного и неподвижного атома, определяемая только временем жизни естественной шириной спектральной линии. Ширину контура спектральной линии принято определять как разность частот, на которых интенсивность равна половине максимального значения. Частотой перехода называют частоту, соответствуюшую максимуму спектральной линии. Форма спектральной линии может быть представлена так называемой лоренцевой кривой совпадающей с резонансной кривой колебательного контура. Реальные наблюдаемые спектральные линии имеют ширину больше естественной.

Уширение спектральной линии из-за столкновений. В газе происходят упругие и неупругие столкновения частиц. При упругих столкновениях суммарная кинетическая энергия сталкивающихся частиц не изменяется: частицы не обмениваются внутренней энергией и не переходят на другие энергетические уровни. При неупругих столкновениях суммарная кинетическая энергия сталкивающихся частиц либо возрастает, либо убывает. В этом случае изменяется внутренняя энергия сталкивающихся частиц, связанная с электронными, колебательными и вращательными уровнями.

В результате неупругих столкновений происходит сокращение времени жизни рассматриваемых частиц в данном энергетическом состоянии до времени среднего пробега между двумя столкновениями, что эквивалентно увеличению ширины спектральной линии.

Вероятность столкновений частиц, следовательно, вероятность квантовых переходов одинаковы для частиц газа. Поэтому форма и ширина спектральной линии всего газа и каждой частицы одинаковы, при этом ширина линии газа и частиц стала больше естественной спектральной линии. Такой процесс называют уширением спектральной линии.

Однородное уширение наблюдается также в случае столкновения частиц газа со стенками, ограничивающими объём газа. Влияние этих столкновений на ширину спектральной линии становится основным при малом давлении газа, когда вероятность столкновений частиц мала.

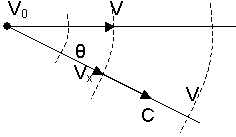
Доплеровское уширение спектральной линии. Это уширение связано с эффектом Доплера, т. е. с зависимостью наблюдаемой частоты излучения от скорости движения излучателя. Если источник, создающий в неподвижном состоянии монохроматическое излучение с частотой, движется со скоростью в сторону к наблюдателю так, что проэкция скорости на направление наблюдения составляет, то наблюдатель регистрирует более высокую частоту излучения.

где с - фазовая скорость распространения волны; 0 - угол между направлениями скорости излучателя и наблюдения.

В квантовых системах источниками излучения являются атомы или молекулы. В газообразной среде при термодинамическом равновесии скорости частиц распределены по закону Максвелла- Больцмана. Поэтому и форма спектральной линии всего вещества – будет связана с этим распределением. В спектре, регистрируемом наблюдателем, должен быть непрерывный набор частиц, так как разные атомы движутся с разными скоростями относительно наблюдателя. Учитывая лишь проекции скорости в распределении Максвелла- Больцмана, можно получить следующее выражение для формы доплеровской спектральной линии:

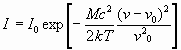
Эта зависимость является гауссовой функцией. Соответствующая значению ширина линии.

С увеличением массы частиц М и понижением температуры Т ширина линии уменьшается.

Вследствие эффекта Доплера спектральная линия всего вещества не совпадает со спектральной линией отдельной частицы. Наблюдаемая спектральная линия вещества представляет собой суперпозицию спектральных линий всех частиц вещества, т. е. линий с различными центральными частотами. Для лёгких частиц при обычной температуре ширина доплеровской линии в оптическом диапазоне может превышать естественную ширину линии на несколько порядков и достигать значения более1ГГц.

Процесс, при котором форма спектральной линии всего вещества не совпадает с формой спектральной линии каждой частицы, называют неоднородным уширением спектральной линии. В рассмотренном случае причиной неоднородного уширения был эффект Доплера. Форма доплеровской спектральной линии описывается гауссовой функцией. Если распределение скоростей частиц отличается от максвелловского, то и форма доплеровской спектральной линии будет отличаться от гауссовой функции, но уширение останется неоднородным.

Другие причины уширения спектральной линии. В квантовых приборах широко используют твёрдые вещества с примесными ионами, квантовые переходы которых являются рабочими. Колебания кристаллической решетки модулируют электрическое поле в том месте, где находится ион, и, следовательно, модулируют положение его энергетических уровней и увеличивает ширину спектральной линии. Кроме того, ширина линии увеличивается вследствие тепловых колебаний самих ионов. Причиной уширения спектральной линии твёрдого тела может быть пространственная неоднородность физических параметров среды или неоднородности электрического и магнитного полей. Эти неоднородности будут вызывать неоднородное уширение спектральной линии. Причиной уширения может быть также электромагнитное излучение, вызывающее вынужденные переходы между рассматриваемыми уровнями и приводящее к изменению времени жизни частицы. Поэтому, например, процесс генерации излучения в квантовых приборах будут приводить к изменению ширины линии

Спектральные коэффициенты Эйнштейна. Введённые ранее коэффициенты Эйнштейна определяют мощность, излучаемую или поглощаемую во всём спектральном диапазоне данного перехода между ними. Поэтому их называют интегральными коэффициентами Эйнштейна. Если их необходимо учитывать частотное распределение излучаемой или поглощаемой мощности, то используют спектральные коэффициенты Эйнштейна a_ji, b_ji, b_ij, которые связаны с А_ji, В_ji и В_ij соотношениями

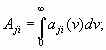
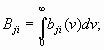
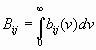
Частотная зависимость всех спектральных коэффициентов одинакова и совпадает с формой контура спектральной линии данного перехода – лоренцевой или гауссовой кривыми. Однако с введением коэффициентов а, и следует уточнить также понятие населённости уровней. Под населённостью любого уровня следует понимать частиц в единице объёма, энергия которых попадает в пределы размытости уровня по энергии. Таким образом, число спонтанных и вынужденных переходов в единичном частном интервале вблизи частоты в единицу времени можно записать с использованием дифференциальных коэффициентов Эйнштейна в виде.

8.4. Возможность усиления и генерации в квантовых системах

Возможность усиления и генерации в квантовых приборах связана с наличием вынужденного излучения в среде, на которую воздействует электромагнитное поле. Однако при этом происходят вынужденные переходы с поглощением энергии и релаксационные переходы. Вынужденные переходы с излучением и поглощением энергии имеют резонансный характер, так как происходят при совпадении частоты поля с частотой квантового перехода, точнее, когда частота поля находятся в пределах спектральной линии вещества.

Рассмотрим обмен энергии между полем и веществом. Будем предполагать, что вещество имеет два энергетических уровня с населённостями N₁ и N₂, а частота внешнего поля равна частоте квантового перехода v₂₁ . При объёмной плотности энергии число вынужденных переходов в единицу времени в единицу объёма с выделением энергии с учётом

n₁₂ = Bu_vN₂,

а выделяемая при этих переходах энергия в единице объёма в единицу времени, т. е. мощность,

Pвыд = n₂₁hv₂₁ = Bu_vN₂hv₂₁.

Аналогично число вынужденных переходов с поглощением энергии и поглощаемая от внешнего поля мощность в единице объёма соответственно равны:

n₁₂ = Bu_vN₁

Pпогл = n₁₂hv₂₁ = Bu_vN₁hv₂₁

С учётом изменение мощности электромагнитного поля. Назовём эту величину мощностью взаимодействия. P = Pвыд - Pпогл

Если Р>0, т. е. выделяемая мощность превышает поглощаемую, то в системе происходит увеличение энергии поля, или усиление электромагнитного поля. При Р<0 преобладает поглащение энергии энергия внешнего поля убывает.

В обычном состоянии термодинамического равновесия населенность верхнего уровня меньше, чем нижнего N₂<N₁, в соответствии с законом Больцмана. Поэтому вещество в этом состоянии поглощает энергию внешнего поля (Р < 0), так как число квантовых переходов снизу вверх (1→2) с поглощением энергии больше числа квантовых переходов сверху вниз (2→1) с выделением энергии.

Соотношение N₂>N₁ является обратным по отношению к состоянию термодинамического равновесия, когда N₂<N₁. Поэтому состояние, при котором N₂>N₁, т. е. возможно усиление, называют состоянием с инверсией населённостей уровней.

Закон Больцмана справедливый только для термодинамического равновесия, можно записать

Величину Тп называют температурой перехода. В состоянии термодинамического равновесия N₁>N₂, т.е. Тп>0. Если формально воспользоваться N₂>N₁, то получится отрицательная температура перехода

Тп<0. Только в состоянии термодинамического равновесия температура перехода совпадёт с истинной температурой вещества Т. Условия усиления N₂>N₁ эквивалентно отрицательной температуре перехода Тп<0. Поэтому состояние с инверсией населённостей уровней иногда называют состоянием с отрицательной температурой, а неравенство Тп<0 - условием усиления в квантовых системах. Среда, в которой имеется состояние с инверсией населённостей, называется также активной средой, так как в ней возможно усиление электрического поля.

8.5. Взаимодействие бегущих электромагнитных волн с активной средой

Предположим, что электромагнитная волна падает на активную среду и распространяется в ней в виде плоской волны по направлению оси. Пусть S - поток энергии через единичное поперечное сечение – изменяется при прохождении излучения через вещество, так как в нём происходят вынужденные переходы с выделением и поглощением энергии. Изменения в слое за 1 с, т. е. изменение мощности.

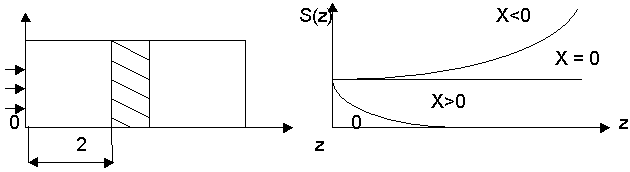
Рис. 8.4

Поток энергии связан с объёмной плотностью энергии и групповой скоростью соотношением.

Исключая u_v , получаем:

или

где, χ- коэффициентом поглощения. Сначала будем считать, что объемная плотность энергии в веществе на столько мала, что можно пренебречь изменением населенности уровней N₁ и N₂. Тогда (N₁- N₂) не зависит от координаты z, т.е. не зависит от z коэффициент χ и интегрирование приводит к формуле:

S(z)=S(0)exp(-χz),

где S(0)- плотность потока энергии в начале образца (z = 0).

Полученная формула называется интегральным законом Бугера.

Из уравнения коэффициента поглощения следует, что при N₁>N₂ (нет инверсии населенностей) и закон описывает поглощение энергии внешнего поля в веществе, а χ имеет смысл коэффициента (показателя) поглощения, показывающего, на кокой длинне энергия волны убывает в е = 2,72 раза.

При N₂>N₁ (инверсия населенностей) χ<0, поэтому отражает усиление поля в веществе. В этом случае говорят об отрицательном коэффициенте поглощения или вводят понятие показатель усиления активной среды:

χ _а = - χ = Bhυ(N₂-N₁)/υг.

Тогда закон Бугера можно записать

S(z)=S(0)exp (χ_az)

Проведенное рассмотрение не учитывало потерь энергии в среде, пропорциональных проходящей мощности S. Будем считать, что эти потери распределены равномерно по координате z. Тогда дифференциальный закон Бугера можно записать в более общем виде:

dS(z)/dz=[χ_а (υ0)-α]S(z)

Потери в активной среде ослабляют усилительный эффект и вызывают ограничение проходящей мощности. С учетом потерь интегральный закон Бугера выглядит так:

S(z)=S(0) exp (χ_a-α)z

При увеличении проходящей мощности необходимо учитывать зависимость χа от z. При небольших потерях в активной среде χа=α переходит в χа. В этом случае предельная мощность получается практически при наступлении насыщения перехода. Впред не зависит от входной мощности S(0). На рисунке показана зависимость S(z) при различных значениях S(0):

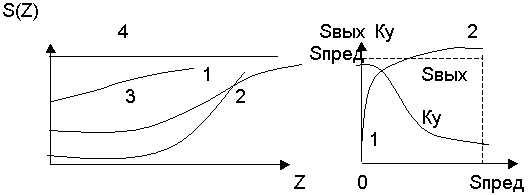
Контрольные вопросы.

1. Виды квантовых переходов. Правило Бора.
2. Понятие о населенностях уровней. Закон Больцмана.
3. Вынужденные переходы частиц между уровнями. Излучательные и безызлучательные переходы. Вероятность перехода и их число.
4. Закон Бугера. Возможность усиления электромагнитных волн веществом. Инверсия населенности уровней.