7.5.1. Последовательное декодирование

7.5.2. Сравнение декодирования по алгоритму Витерби с последовательным декодированием и их ограничения

7.5.3. Декодирование с обратной связью

7.5.1. Последовательное декодирование

Ранее, до того как Витерби открыл оптимальный алгоритм декодирования сверточных кодов, существовали и другие алгоритмы. Самым первым был алгоритм последовательного декодирования, предложенный Уозенкрафтом (Wozencraft) [24, 25] и модифицированный Фано (Fano) [2]. В ходе работы последовательного декодера генерируется гипотеза о переданной последовательности кодовых слов и рассчитывается метрика между этой гипотезой и принятым сигналом. Эта процедура продолжается до тех пор, пока метрика показывает, что выбор гипотезы правдоподобен, в противном случае гипотеза последовательно заменяется, пока не будет найдена наиболее правдоподобная. Поиск при этом происходит методом проб и ошибок. Для мягкого или жесткого декодирования можно разработать последовательный декодер, но обычно мягкого декодирования стараются избегать из-за сложных расчетов и большой требовательности к памяти.

Рассмотрим ситуацию, когда используется кодер, изображенный на рис. 7.3, и последовательность m=11011 кодирована в последовательность кодовых слов U=1101010001, как было в примере 7.1. Допустим, что принятая последовательность Z является, фактически, правильной передачей U. У декодера имеется копия кодового дерева, показанная на рис. 7.6, и он может воспользоваться принятой последовательностью Z для прохождения дерева. Декодер начинает с узла дерева в момент t и генерирует оба пути, исходящие из этого узла. Декодер следует пути, который согласуется с полученными n кодовыми символами. На следующем уровне дерева декодер снова генерирует два пути, выходящие из узла, и следует пути, согласующемуся со второй группой и символов. Продолжая аналогичным образом, декодер быстро перебирает все дерево.

Допустим теперь, что принятая последовательность Z является искаженным кодовым словом U. Декодер начинает с узла дерева в момент и генерирует оба пути, выходящие из этого узла. Если принятые п кодовых символов совпадают с одним из сгенерированных путей, декодер следует этому пути. Если согласования нет, то декодер следует наиболее вероятному пути, но при этом ведет общий подсчет несовпадений между принятыми символами и ответвляющимися словами на пути следования. Если две ветви оказываются равновероятными, то приемник делает произвольный выбор, как и в случае с нулевым входным путем. На каждом уровне дерева декодер генерирует новые ветви и сравнивает их со следующим набором п принятых кодовых символов. Поиск продолжается до тех пор, пока все дерево не будет пройдено по наиболее вероятному пути, и при этом составляется счет несовпадений.

Если счет несовпадений превышает некоторое число (оно может увеличиваться после прохождения дерева), декодер решает, что он находится на неправильном пути, отбрасывая этот путь и повторяет все снова. Декодер помнит список отброшенных путей, чтобы иметь возможность избежать их при следующем прохождении дерева. Допустим, кодер, представленный на рис. 7.3, кодирует информационную последовательность m=11011 в последовательность кодовых слов U, как показано на рис. 7.1. Предположим, что четвертый и седьмой биты переданной последовательности U приняты с ошибкой.

Давайте проследим за траекторией пути декодирования на рис. 7.23. Допустим; что критерием возврата и повторного прохождения путей будет общий счет не согласующихся путей, равный 3. На рис. 7.23 числа у путей прохождения представляют собой текущее значение счетчика несовпадений. Итак, прохождение дерева будет иметь следующий вид.

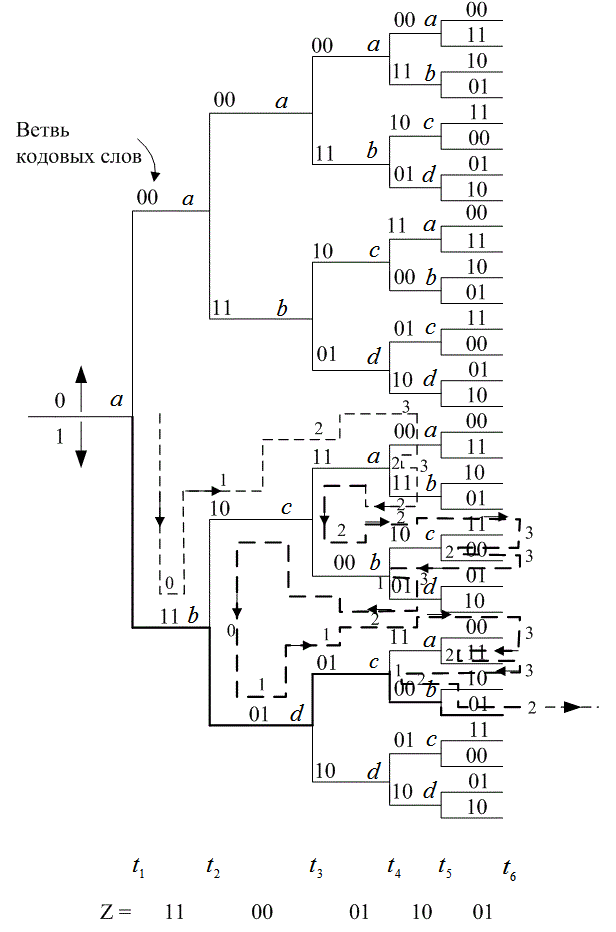
Рис. 7.23. Схема последовательного декодирования

1. В момент времени мы принимаем символы 11 и сравниваем их с ответвляющимся словами, исходящими из первого узла.

2. Наиболее вероятна та ветвь, у которой ответвляющееся слово 11 (соответствующее входной битовой единице или ответвлению вниз), поэтому декодер решает, что входная битовая единица правильно декодирована, и переходит на следующий уровень.

3. В момент на этом втором уровне декодер принимает символы 00 и сравнивает их с возможными ответвленными словами 10 и 01.

4. Здесь нет "хорошего" пути; поэтому декодер произвольно выбирает путь, соответствующий входному битовому нулю (или ответвляющемуся слову 10), и счетчик несовпадений регистрирует 1.

5. В момент времени декодер принимает символы 01 и сравнивает их на третьем уровне с ответвляющимися словами 11 и 00.

6. Здесь снова ни один из путей не имеет преимуществ. Декодер произвольно выбирает нулевой входной путь (или ответвленное слово 11), и счетчик несовпадений возрастает до 2.

7. В момент декодер принимает символы 10 и сравнивает их на четвертом уровне с ответвленными словами 00 и 11.

8. Здесь снова ни один из путей не имеет преимуществ, и декодер произвольно выбирает нулевой входной путь (или ответвленное слово 00); счетчик несовпадений возрастает до 3.

9. Поскольку счет несовпадений, равный 3, соответствует точке возврата, декодер "делает откат" и пробует альтернативный путь. Счетчик переустанавливается на 2 несовпадения.

10. Альтернативный путь на четвертом уровне соответствует пути входной битовой единицы (или ответвленному слову 11). Декодер принимает этот путь, но после сравнения его с принятыми символами 10 несовпадение остается равным 1, и счетчик устанавливается равным 3.

11. Счет 3 является критерием точки возврата, поэтому декодер делает откат назад с этого пути, и счетчик снова устанавливается на 2. На данном уровне все альтернативные пути использованы, поэтому декодер возвращается на узел в момент и переустанавливает счетчик на 1.

12. В узле декодер сравнивает символы, принятые в момент времени а именно 01, с неиспользованным путем 00. В данном случае несовпадение равно 1, и счетчик устанавливается на 2.

13. В узле декодер следует за ответвляющимся словом 10, которое совпадает с принятым в момент кодовым символом 10. Счетчик остается равным 2.

14. В узле ни один из путей не имеет преимуществ, и декодер, как и определяется правилами, следует верхней ветви. Счетчик устанавливается на 3 несовпадения.

15. При таком счете декодер делает откат, переустанавливает счетчик на 2 и пробует альтернативный путь в узле . Поскольку другим ответвляющимся словом является 00, снова получаем одно несовпадение с принятым в момент кодовым символом 01, и счетчик устанавливается равным 3.

16. Декодер уходит с этого пути, и счетчик переустанавливается на 2. На этом уровне все альтернативные пути исправлены, по этому декодер возвращается на узел в момент и переустанавливает счетчик на 1.

17. Декодер пробует альтернативные пути в узле , метрика которого возрастает до 3, поскольку в ответвляющемся слове имеется не совпадение в двух позициях. В этот момент декодер должен сделать откат всех путей до момента , поскольку все пути более высоких уровней уже использованы. Счетчик снова переустановлен на нуль.

18. В узле декодер следует ответвляющемуся слову 01. Поскольку имеются не совпадения в одной позиции с принятыми в момент кодовыми символами 00, то счетчик устанавливается на 1.

Далее декодер продолжает свои поиски таким же образом. Как видно из рис. 7.23, финальный путь, счетчик которого не нарушает критерия точки возврата, дает правильно декодированную информационную последовательность 11011. Последовательное декодирование можно понимать как тактику проб и ошибок для поиска правильного пути на кодовом дереве. Поиск осуществляется последовательно; всегда рассматривается только один путь за раз. Если принимается не правильное решение, последующие пути будут ошибочными. Декодер может со временем распознать ошибку, отслеживая метрики пути. Алгоритм напоминает путешественника, отыскивающего путь на карте дорог. До тех пор, пока путешественник видит, что дорожные ориентиры соответствуют таковым на карте, он продолжает путь. Когда он замечает странные ориентиры (увеличение его своеобразной метрики), в конце концов приходит к выводу, что он находиться на не правильном пути, и возвращается к точке, где он может узнать ориентиры (его метрика возвращается в приемлемые рамки). Тогда он пробует альтернативный путь.

7.5.2. Сравнение декодирования по алгоритму Витерби с последовательным декодированием и их ограничения

Главный недостаток декодирования по алгоритму Витерби заключается в том, что, когда вероятность появления ошибки экспоненциально убывает с ростом длины кодового ограничения, число кодовых состояний, а значит сложность декодера, экспоненциально растет с увеличением длины кодового ограничения. С другой стороны, вычислительная сложность алгоритма Витерби является независимой характеристикой канала (в отличие от жесткого и мягкого декодирования, которые требуют обычного увеличения объемов вычислений). Последовательное декодирование асимптотически достигает той же вероятности появления ошибки, что и декодирование по принципу максимального правдоподобия, но без поиска всех возможных состояний. Фактически при последовательном декодировании число перебираемых состояний существенно независимо от длины кодового ограничения, и это позволяет использовать очень большие (К = 41) длины кодового ограничения. Это является важным фактором при обеспечении таких низких вероятностей появления ошибок. Основным недостатком последовательного декодирования является то, что количество перебираемых метрик состояний является случайной величиной. Для последовательного декодирования ожидаемое число неудачных гипотез и повторных переборов является функцией канального отношения сигнал/шум (signal to noise ratio — SNR). При низком SNR приходится перебирать больше гипотез, чем при высоком SNR. Из-за такой изменчивости вычислительной нагрузки, поступившие последовательности необходимо сохранять в буфере памяти. При низком SNR последовательности поступают в буфер до тех пор, пока декодер не сможет найти вероятную гипотезу. Если средняя скорость передачи символов превышает среднюю скорость декодирования, буфер будет переполняться, вне зависимости от его емкости, и данные будут теряться. Обычно, пока идет переполнение, буфер убирает данные без ошибок, в то время как декодер пытается выполнить процедуру восстановления. Порог переполнения буфера существенно зависит от SNR. Поэтому важным техническим требованием к последовательному декодеру является вероятность переполнения буфера.

На рис. 7.24 показаны типичные кривые, отображающие зависимость от для двух распространенных схем — декодирования по алгоритму Витерби и последовательного декодирования. Здесь сравниваются их характеристики при использовании когерентной модуляции BPSK в канале AWGN. Сравниваются кривые для декодирования по алгоритму Витерби (степень кодирования 1/2 и 1/3, К = 7, жесткое декодирование), декодирования по алгоритму Витерби (степень кодирования 1/2 и 1/3, К=7, мягкое декодирование) и последовательного декодирования (степень кодирования 1/2 и 1/3, К=41, жесткое декодирование), из рис- 7.24 можно видеть, что при последовательном декодировании можно достичь эффективности кодирования порядка 8 дБ при . Поскольку в работе Шеннона (Shannon) [26] предсказывается потенциальная эффективность кодирования около 11 дБ, по сравнению с не кодированной передачей с модуляцией BPSK, похоже, что, в основном, теоретически достижимые возможности уже получены.

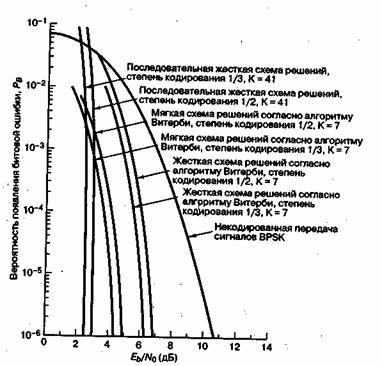
Рис. 7.24. Вероятности появления битовых ошибок для различных схем декодирования по алгоритму Витерби и последовательного декодирования, при когерентной модуляции BPSK в канале AWGN. (Перепечатано с разрешения авторов из J. К. Отит and В. К. Levitt, "Coded Error Probability Evaluation for Antijam Communication Systems". IEEE Trans. Commun., vol. COM30, n. 5, May, 1982, Fig. 4, p. 900. © 1982, IEEE.)

7.5.3. Декодирование с обратной связью

Декодер с обратной Связью реализует жесткую схему принятия решений относительно информационного бита в разряде j, исходя при этом из метрик, полученных из разрядов j, j+1…, j+т, где т—заранее установленное положительное целое число. Длина упреждения (look-ahead length) L определяется как L=m+1, количество принятых кодовых символов, выраженных через соответствующее число входных битов, задействованных для декодирования информационного бита. Решение о том, является ли информационный бит нулем или единицей, принимается в зависимости от того, на какой ветви путь минимального расстояния Хэмминга переходит в окне упреждения(look-ahead window) из разряда J в разряд j+т. Поясним это на конкретном примере. Рассмотрим декодер с обратной связью, предназначенный для сверточного кода со степенью кодирования 1/2, который показан на рис. 7.3. На рис. 7.25 приведена древовидная диаграмма и работа декодера с обратной связью при L=3. Иными словами, при декодировании бита из ветви j декодер содержит пути из ветвей j, j + 1 и j + 2.

Начиная из первой ветви, декодер вычисляет (восемь) совокупных метрик путей расстояния Хэмминга и решает, что бит для первой ветви является нулевым, если путь минимального расстояния содержится в верхней части дерева, и единичным, если путь минимального расстояния находится в нижней части дерева. Пусть принята последовательность Z=1100010001. Рассмотрим восемь путей от момента до момента t3 в блоке, обозначенном на рис. 7.24 буквой А, и рассчитаем метрики, сравнивая эти восемь путей для первых шести принятых кодовых символов (три ветви вглубь умножить на два символа для ветви). Выписав метрики Хэмминга общих путей (начиная с верхнего пути), видим, что они имеют следующие значения.

Метрики верхней части 3, 3, 6, 4

Метрики нижней части 2,2,1,3

Видим, что наименьшая метрика содержится в нижней части дерева. Следовательно, первый декодированный бит является единицей (и определяется сдвигом вниз на дереве). Следующий шаг будет состоять в расширении нижней части дерева (выживающий путь) на один разряд глубже, и здесь снова вычисляется восемь метрик, теперь уже для моментов . Получив, таким образом, два декодированных символа, мы теперь можем сдвинуться на два символа вправо и снова начать расчет метрик путей, но уже для шести кодовых символов. Эта процедура видна в блоке, обозначенном на рис. 7.25 буквой В. И снова, проследив метрики верхних и нижних путей, находим следующее.

Метрики верхней части 2, 4, 3, 3

Метрики нижней части 3, 1, 4, 4

Минимальная метрика для ожидаемой принятой последовательности находится в нижней части блока В. Следовательно, второй декодируемый бит также является единицей.

Таким образом, процедура продолжается до тех пор, пока не будет декодировано все сообщение целиком. Декодер называется декодером с обратной связью, поскольку найденное решение подается обратно в декодер, чтобы потом использовать его в определении подмножества кодовых путей, которые будут рассматриваться следующими. В канале BSC декодер с обратной связью может оказаться, почти таким же эффективным, как и декодер, работающий по алгоритму Витерби (17). Кроме того, он может исправлять все наиболее вероятные ошибочные комбинации, а именно — те, которые имеют весовой коэффициент или менее, где df — просвет кода. Важным параметром разработки сверточного декодера с обратной связью является L, длина упреждения. Увеличение L приводит к повышению эффективности кодирования, но при этом растет сложность конструкции декодера.

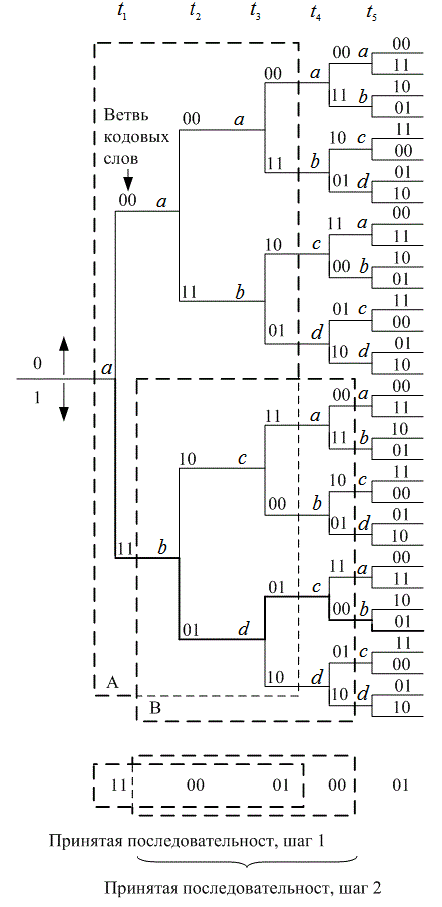
Рис. 7.25. Пример декодирования с обратной связью