В настоящее время в связи с широким распространением цифровых систем передачи и обработки информации возникла необходимость изучения принципов формирования и методов оценки характеристик таких сигналов. Как известно из предыдущего материала, формирование цифрового сигнала включает в себя следующие операции: дискретизацию аналогового сигнала во времени, квантование дискретного сигнала по уровню и перекодирование значений квантованного сигнала из одной системы счисления в другую (в подавляющем большинстве случаев – в двоичную). Мы начнем с рассмотрения спектральных характеристик дискретного сигнала.

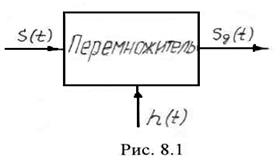Напомним, что дискретный сигнал (или дискретная последовательность) формируется при помощи перемножителя (рис. 8.1), на один из входов которого поступает аналоговый сигнал , а на второй – последовательность коротких импульсов с периодом следования , значение которого определяется теоремой Котельникова

,

где или – верхняя граничная частота аналогового сигнала .

Тогда дискретный сигнал может быть описан выражением

. (8.1)

Вычислим спектр дискретного сигнала. В первую очередь, рассмотрим второй сомножитель выражения (8.1)

. (8.2)

Этот сомножитель представляет собой математическое описание периодической последовательности импульсов. Обычно при осуществлении операции дискретизации форма импульса выбирается прямоугольной. Поэтому в дальнейшем будем полагать, что представляет собой периодическую последовательность прямоугольных импульсов амплитудой и длительностью , следующих с периодом .

Как известно, периодическая последовательность прямоугольных импульсов может быть представлена рядом Фурье, который для рассматриваемого случая принимает вид

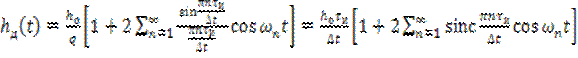. (8.3)

где , – скважность, .

Тогда с учетом (8.3) выражение (8.1) принимает вид

. (8.4)

Применим к (8.4) прямое преобразование Фурье

.

Подстановка в эту формулу выражения (8.4) дает

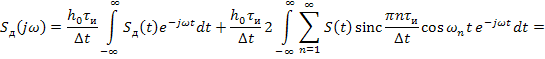
. (8.5)

Интеграл первого слагаемого в (8.5) представляет собой спектр исходного аналогового сигнала. Представим второе слагаемое в (8.5) в виде

. (8.6)

Учитывая, что , запишем

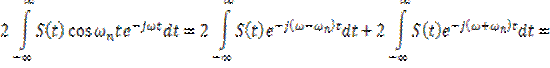
. (8.7)

Тогда с учетом (8.6) и (8.7) выражение (8.5) принимает вид

. (8.8)

Здесь пределы суммирования составляют в виду того, что спектр распространяется на область отрицательных частот.

Дальнейший спектральный анализ дискретного сигнала существенно упрощается, если предположить, что дискретизация осуществляется последовательностью прямоугольных импульсов единичной площади. В этом случае амплитуда импульса и выражение (8.8) запишется следующим образом

. (8.9)

Если устремить , т.е. перейти к последовательности бесконечно коротких импульсов ( -импульсов), т.е.

, (8.10)

то с учетом того, что , спектральная функция дискретного сигнала окончательно принимает вид

. (8.11)

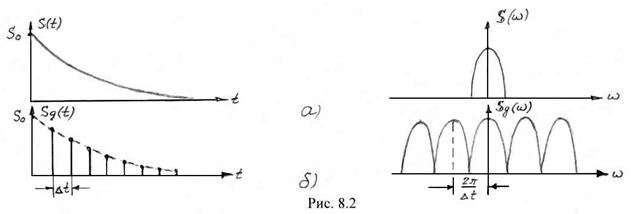
На рис. 8.2 а) представлен аналоговый сигнал и условное изображение модуля его спектральной функции , а на рис. 8.2б – дискретный сигнал и модуль его спектра . Из выражения (8.11) и рис. 8.2 следует, что спектр дискретного сигнала представляет собой бесконечную последовательность копий спектра исходного аналогового сигнала , причем эта последовательность носит периодический характер. Расстояние по оси частот между отдельными копиями составляет (или ), что соответствует периоду последовательности копий на оси частот. Отметим, что (или ) – это частота дискретизации. Таким образом, период спектральной функции дискретного сигнала равен частоте дискретизации.