10.2. Основные типы световодов
10.3. Особенности поперечных структур поля в световодах
10.1. Преимущества световодов
- Световоды обладают большой пропускной способностью (многоканальностью).
- Световоды не подвержены воздействию внешних ЭМП (наводки, молнии и т.д.).
- Малогабаритны (вес и масса малы).
- Отсутствие металлических проводников, нет металла дорогостоящего (медь, серебро, золото).
10.2. Основные типы световодов
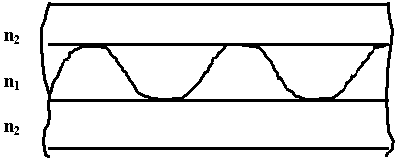
1. Планарный световод - представляет собой тонкую стеклянную пленку (плоскую).
В увеличенном виде выглядит следующем образом:
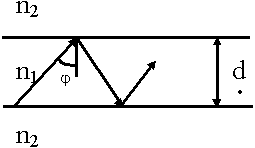
n1 - всегда > n2 - показатель преломления окружающей cреды, n1 - показатель преломления пленки. n1 > n2
Такой слой может направлять ЭМВ вдоль границы. Физической основой передачи энергии оптического диапазона во всех типах световодов является эффект полного внутреннего отражения. Если 
> кр, то волна распространяется, если это условие не выполняется, то часть энергии выходит в окружающее пространство и передача энергии не возможна.
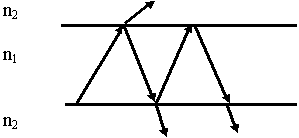
Основное назначение планарных световодов - реализация на их базе различных устройств по обработке информации в оптическом диапазоне (фильтры, различные делители энергии, направленные ответвители и т.д.).
2. Волоконный световод - тонкая стеклянная двухслойная нить в поперечном сечении. Имеет вид:
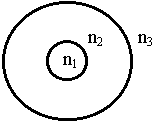
n1 - показатель преломления сердцевины;
n2 - показатель преломления оболочки;
n3 - показатель преломления окружающей cреды.
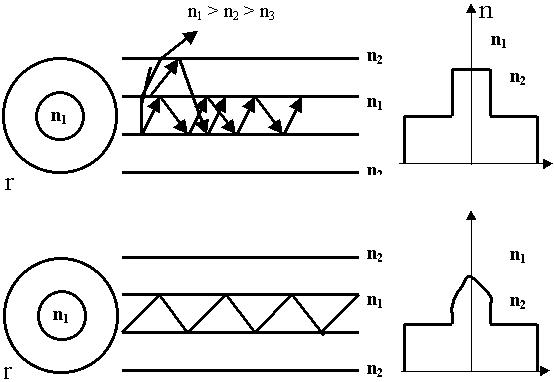
Различают ступенчатые и градиентные световоды. Если дискретно меняется показатель преломления, то такое волокно называется ступенчатым световодом.
Другая разновидность световода - световод с непрерывным распределением показателя преломления, их еще называют градиентными. Они отличаются от ступенчатых световодов тем, что показатель изменяется по определенному закону.
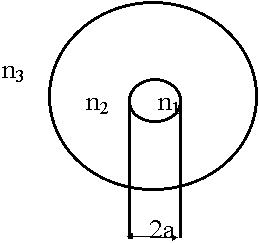
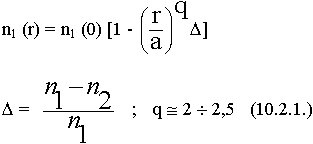
показатель степени
В центре n1 max и убывает по параболе к оболочке. Такой световод может фокусировать.
В настоящее время строгие методы расчета базируются на 2-х подходах:
- Используют геометро-оптическое представление процессов в световодах.
В основе лежит первый и второй закон Снеллиусса.
- Используют полевое описание (представление) при распространении волн.
При работе с планарными световодами чаще используют первый подход (методы геометрической оптики). Для анализа волоконных световодов используют второй метод.
10.3. Особенности поперечных структур поля в световодах
Фазовая скорость в световодах. Vф 
= 
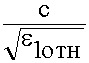< c
Vф всегда меньше скорости света (с)
m = 
- коэффициент замедления.
m всегда > 1. Световод замедляет волны.
Vф =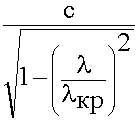 
- в волноводе
m = = 
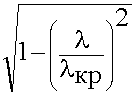< 1 (10.3.1.)
Волновод ускоряет волны.
Составляющие полей удовлетворяют условию:
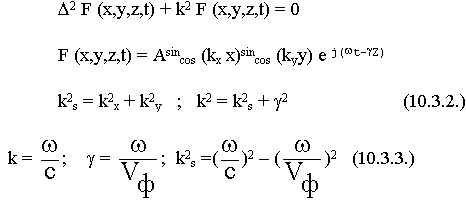
Рассмотрим выражение (10.3.3.) для световодов, когда Vф < c, то :
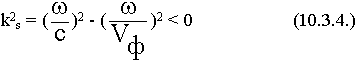
Величина ks - мнимая.
Формально отсюда, что kx и ky чисто мнимые величины.
kx = j 
; ky = j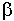 
- могут оба сразу.
или либо kx, либо ky
sin j x = j sh x ; cos j x = ch x
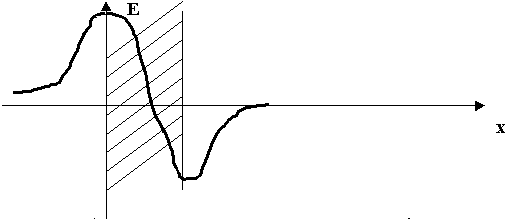
В поперечном сечении поля описываются непериодическими функциями (гиперболическими).
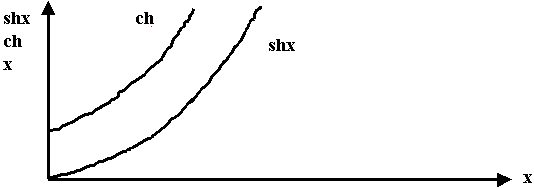
Вопрос: Что означает, что так распределено поле - Е ?
Что надо сделать чтобы было max поле?
Ответ: Сделать стенку из диэлектрика.
В линиях передачи с медленными волнами поле распределено неравномерно, оно прижато к границе раздела.
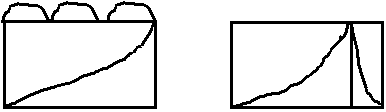
Такая ситуация напоминает поверхностные волны, которые как бы прилипают к поверхности.
10.4. Планарный световод
Задача ставится следующим образом:
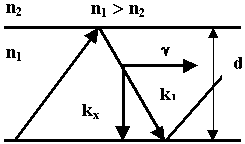
Имеется пластинка, толщиной d. На границе раздела сред выполняется условие полного внутреннего отражения. Цель определить критический размер d и 
кр, когда слой может направлять электромагнитные колебания оптического диапазона.
Выделим основные параметры внутри слоя. Направление волнового процесса вдоль оси Z -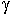 
, поперечное волновое число - kx. В поперечном сечении в результате отражения от границ раздела устанавливается стоячая волна.
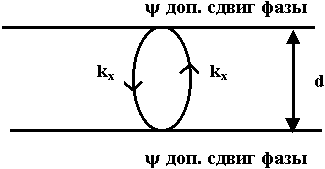
При отражении от границы раздела появляется дополнительный сдвиг фаз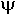 
. Сколько же всего ? Вычислим общий набег фазы:
1) kx d + 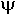(от верхней до нижней)
2) kx d + 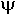(от нижней до верхней)
Синфазное сложение будет тогда, когда целое число
kx d + 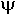+ kx d + 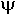= 2
(m - 1)
m = 1 , 2 . . . (10.4.1.)
или kx d = (m - 1) (10.4.2.)
Выражение (10.4.2.) можно использовать для расчета критической длины волны, передаваемой в пластинке. Представим величину kx через параметры среды и пластинки:
kx = k1 cos ; 
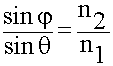(10.4.3.)
Поскольку явление полного внутреннего отражения, то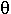 
= 900 sin 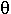= 1
sin = 
0 = 0кр
cos = 
=
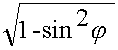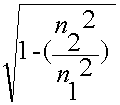(10.4.4.)
Окончательно:
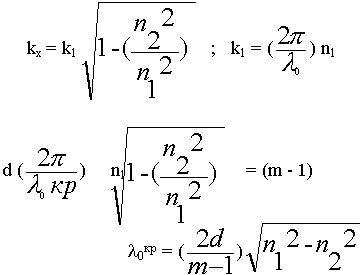
0кр зависит от размеров (толщины) и разности показателей преломления, 0кр при
m = 1 становится, б/б. Волновой процесс идет на любой частоте.
Каждому значению m соответствует своя критическая длина волны и своя структура поля, своя мода.
При m = 1 , кр =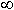 
. Такая волна называется основной волной планарного световода. Это несколько искаженная самой пластинкой плоская ЭМВ. У плоской ЭМВ нет критического режима, она существует на любых частотах.
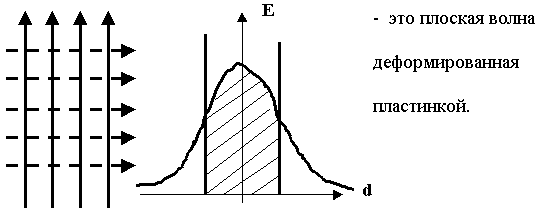
плоская ЭМВ m = 1
Если m = 2
Все остальные типы будут иметь конечные значения кр и начинают распространяться выше своих критических частот. Будущие системы будут работать в одномодовом режиме, чтобы высшие типы не распространялись. Пластинку надо делать с высоким качеством и очень тонкую (1 - 2 мкМ). Специалисты делают по другому. Они обеспечивают уменьшение 0кр при заданной толщине d , уменьшением разности показателей преломления
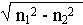
на f1 >> fкр. Идет процесс передачи по световоду (угол велик). условие полного внутреннего отражения выполняется.
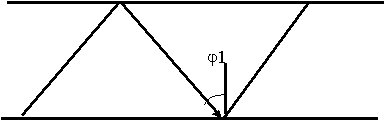
f2 < f1 2 < 1
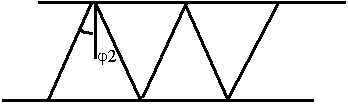
f3 < fкр - условие для выполнения полного внутреннего отражения нет, часть волны уходит в окружающую среду.
10.5. Оптическое волокно
Проследить и выделить результат многократного отражения в цилиндре сложно. Рассмотрим волокно, представляющее собой бесконечную длинную нить.
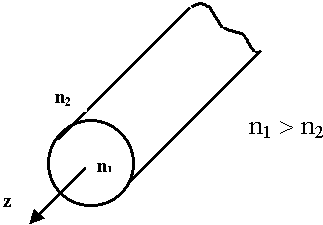
Рассмотрим задачу для Е - волн.
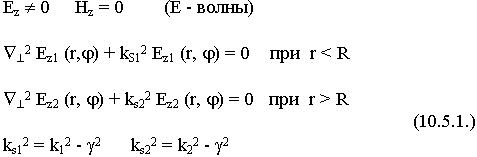
10.5.1. Симметричные волны в оптическом волокне
Рассмотрим частный случай. Симметричные волны в оптическом волокне, симметричные Е - волны, 
= 0. Это соответствует случаю, когда азимутальный индекс, который определяет порядок функции Бесселя n = 0. В цилиндрических координатах в первой среде при r < R.
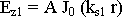- решение волновых уравнений внутри волокна (10.5.2.)
Для поля вне волокна должно выполняться условие уменьшения поля с удалением от стержня. В классе функций Бесселя надо искать условие убывания. Единственной функцией среди цилиндрических (Неймана, Ханкеля и др.) является функция Макдональда Кn (x), у которой при больших значениях аргументов функция уменьшается:
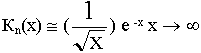- функция непериодическая. (10.5.3.)
Решение для составляющих Еz2:
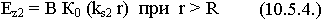
Если известны продольные составляющие, то можно выразить поперечные:
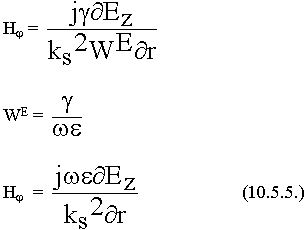
Вычислим две составляющие внутри волокна и вне.
Внутри волокна:
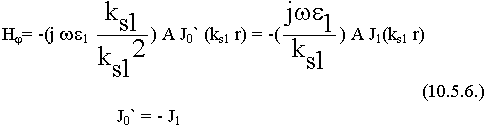
при дифференцировании
Вне волокна:
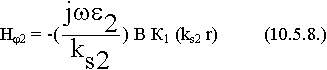
Используем непрерывность касательных составляющих:
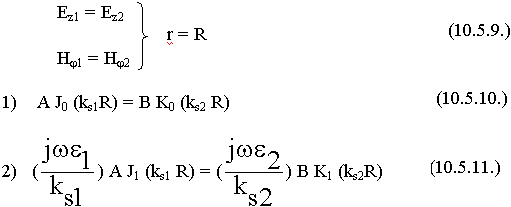
Разделим (10.5.10.) на (10.5.11.):
=
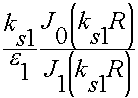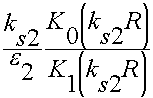(10.5.12.)
В явном виде такое уравнение решить нельзя. Оно трансцендентное, имеет большое множество решений, каждому из которых соответствует своя волна.
Простейшая волна Е01
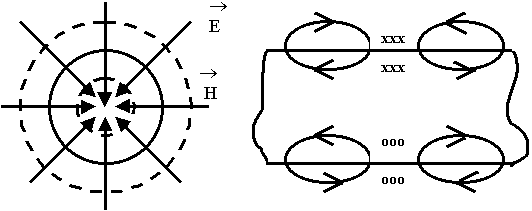
В отличие от волновода часть энергии выходит за пределы.
Возможность полевого электродинамического подхода позволяет рассчитать напряженность электрического и магнитного полей. Законы геометрической оптики позволяют определить углы.
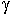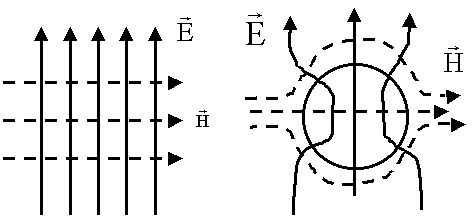
Если ks2 = 0, то = k2=k0n2 - критический режим. Волна выходит в окружающее пространство. 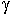- продольное волновое число Vф = с.
10.5.2. Несимметричные волны в оптическом волокне
Наряду с симметричными волнами, в волокне могут существовать и распространяться несимметричные волны.
В случае несимметричных волн, перенос энергии осуществляется гибридными волнами НЕ и ЕН. Для них (Еz 0 , Hz 0). Гибридные волны являются основными волнами в оптических волокнах.
Основная волна НЕ11 - существует на всех частотах. Когда плоская волна распространяется вдоль волокна, она искажается.
Часть энергии передается внутри стержня, часть вне. В стержне волна распространяется медленнее, чем в окружающем пространстве, за счет разности скоростей поле искажается и становится гибридным.
Все кабельные линии связи используют тип волны “Т”.
“Т” - волна. Еz = 0 Hz = 0. Из общего анализа “Т” волна возможна, когда ks = 0:
кр = 
; кр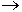 
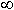
Волна “Т” существует на любых частотах.
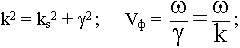Vф не зависит от частоты.
Дисперсия отсутствует в линиях передачи с волной типа “Т”.