5.1. Негармонические периодические сигналы. Разложение в ряд Фурье

5.2. Действующее, среднее значение и мощность периодического негармонического сигнала

5.3. Спектры периодических негармонических сигналов

5.4. Расчет цепей при периодических негармонических воздействиях

5.5. Вопросы и задания для самопроверки

5.1. Негармонические периодические сигналы

При передаче информации по каналам связи в процессе преобразования сигналов в различных устройствах, как правило, используют негармонические колебания, поскольку чисто гармонические колебания не могут являться носителями информации. Для передачи сообщений осуществляют модуляцию гармонического колебания по амплитуде – амплитудная модуляция (AM), частоте – частотная модуляция (ЧМ) или фазе – фазовая модуляция (ФМ), либо используют импульсные сигналы, модулируемые по амплитуде – амплитудно-импульсная модуляция (АИМ), ширине – широтно-импульсная модуляция (ШИМ), временному положению – время-импульсная модуляция (ВИМ). Существуют и другие, более сложные сигналы, формируемые по специальным законам. Отличительной чертой указанных сигналов является сложный негармонический характер. Несинусоидальный вид имеют токи и напряжения, формируемые в различных импульсных и цифровых устройствах, несинусоидальный характер приобретают гармонические сигналы, проходящие через различные нелинейные устройства и т. д. Все это приводит к необходимости разработки специальных методов анализа и синтеза электрических цепей, находящихся под воздействием периодических несинусоидальных и непериодических токов и напряжений. В основе этих методов лежат спектральные представления несинусоидальных воздействий, базирующиеся на разложении в ряд или интеграл Фурье.

Из математического анализа известно, что периодическая негармоническая функция f(t), удовлетворяющая условиям Дирихле, может быть разложена в ряд Фурье: 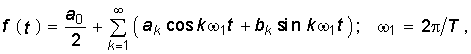   (5.1) где a_k, b_k — коэффициенты разложения, определяемые уравнениями  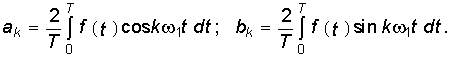  (5.2)

Величина 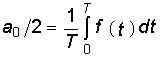представляет среднее за период значение функции f(t) и называется постоянной составляющей.

В теоретических исследованиях обычно вместо формулы (5.1) используют другую, основанную на замене независимой переменной :  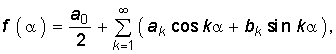  (5.3) где  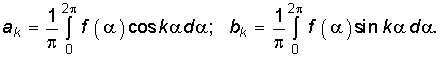  (5.4)

Уравнение (5.3) есть тригонометрическая форма ряда Фурье. При анализе цепей часто удобней пользоваться комплексной формой ряда Фурье, которая может быть получена из (5.3) с помощью формул Эйлера:    (5.5)

Подставив (5.5) в уравнение (5.3), после несложных преобразований получим комплексную форму ряда Фурье: 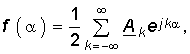   (5.6) где A_k — комплексная амплитуда k-й гармоники:    (5.7) где – амплитуда; – начальная фаза k-й гармоники.

Подставив значения a_k и b_k из (5.4) в (5.7), получим: 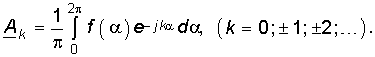   (5.8)

Совокупность амплитуд 0,5А_k = 0,5А_–k в разложении (5.6), отложенных против соответствующих положительных и отрицательных частот, образует симметричный относительно оси координат (вследствие четности коэффициентов а_k) линейчатый амплитудный спектр.

Совокупность ординат _k = –_–k из (5.7), входящих в разложение (5.6) и отложенных против соответствующих положительных и отрицательных частот, образует симметричный относительно начала оси координат (вследствие нечетности коэффициентов b_k) линейчатый фазовый спектр.

Разложение (5.3) можно представить и в другой форме. Если учесть, что а_k = А_kcos _k и b_k = А_ksin _k, то после подстановки в (5.3) получим: 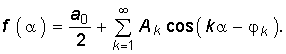   (5.9)

Если рассматривать постоянную составляющую a₀/2 как нулевую гармонику с начальной фазой ₀ = 0, то разложение (5.9) примет вид 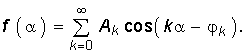   (5.10)

В частном случае, когда функция f(a) симметрична относительно оси ординат (рис. 5.1, а), в разложении (5.3) окажутся только четные (косинусоидальные) гармоники:

   (5.11)

а при симметричности f(a) относительно начала координат (рис. 5.1, б) нечетные гармоники    (5.12)

При сдвиге начала отсчета функции f(a) ее амплитудный спектр не изменяется, а меняется только фазовый спектр. Действительно, сдвинем функцию f(a ) по оси времени влево на t₀ и обозначим .

Тогда разложение (5.9) примет вид 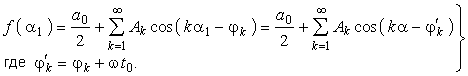   (5.13)

Пример. Разложить в ряд Фурье прямоугольные колебания (рис. 5.1, б). Учитывая, что f(a) симметрична относительно начала координат в разложении (5.3) останутся только синусоидальные гармоники (5.12), где b_k определится согласно (5.4): 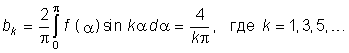Подставив b_k в (5.12), получим разложение в ряд Фурье:    (5.14) Далее сдвинем f(a) на p/2 влево (см. рис. 5.1, а). Тогда согласно (5.13) получим 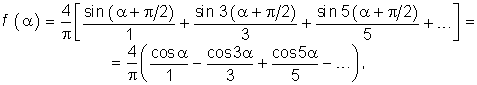   (5.15) т. е. получили разложение по косинусоидальным составляющим как и должно быть для симметричного относительно оси ординат сигнала.

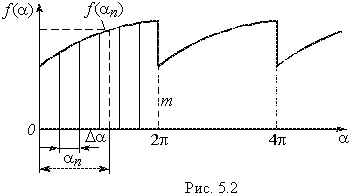
В ряде случаев, когда периодичная функция f(a) задана графически и имеет сложную форму, ее разложение в ряд Фурье можно осуществить графо-аналитическим способом. Его суть заключается в том, что период сигнала Т (рис. 5.2) разбивают на m интервалов, равных , причем точки разрыва f(a) не должны попадать на середину участков разбиения; определяют значение сигнала f(a_n) в середине каждого участка разбиения.

Находят коэффициенты разложения а_k и b_k путем замены интеграла в (5.2) конечной суммой 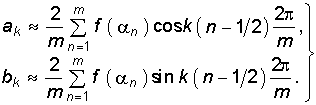   (5.16)

Уравнение (5.16) легко программируется и при вычислении а_k и b_k, может использоваться ЭВМ.

5.2. Действующее, среднее значение и мощность периодического негармонического сигнала

Для определенности положим, что f(t) имеет смысл тока i(t). Тогда действующее значение периодического негармонического тока определяется согласно (3.5), где i(t) определяется уравнением (5.10): 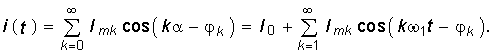   (5.17)

Подставив это значение тока в (3.5), после интегрирования получим 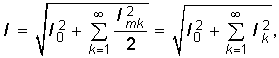   (5.18)

т. е. действующее значение периодического негармонического тока I полностью определяется действующими значениями его гармоник I_k и не зависит от их начальных фаз _k.

Аналогичным образом находим действующее значение периодического несинусоидального напряжения: 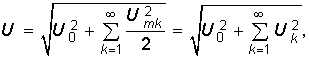   (5.19)

Среднее значение тока определяется согласно общему выражению (3.9). Причем обычно берут среднее значение i(t) по абсолютной величине 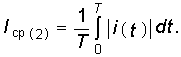   (5.20)

Аналогично определяется U_ср(2).

С точки зрения теории цепей, большой интерес представляет средняя активная мощность негармонического сигнала и распределение ее между отдельными гармониками.

Средняя активная мощность периодического несинусоидального сигнала 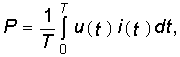   (5.21) где  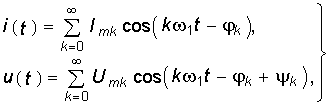  (5.22)

_k — фазовый сдвиг между током и напряжением k-й гармоники.

Подставляя значения i(t) и u(t) из (5.22) в уравнение (5.21), после интегрирования получаем: 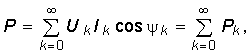   (5.23) т, е. средняя за период активная мощность периодического негармонического сигнала равна сумме мощностей отдельных гармоник. Формула (5.23) является одной из форм широко известного равенства Парсеваля.

Аналогично находим реактивную мощность 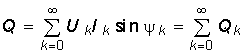   (5.24) и полную мощность  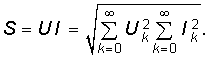  (5.25)

Следует подчеркнуть, что в отличие от гармонических сигналов для негармонических сигналов    (5.26)

Величина P_иcк = носит название мощности искажений и характеризует степень различия в формах тока i(t) и напряжения u(t).

Кроме мощности искажений периодические негармонические сигналы характеризуются еще рядом коэффициентов: мощности, k_м = P/S; формы K_ф = U/U_ср(2); амплитуды K_a = U_m/U; искажений k_и = U₁/U; гармоник k_г = 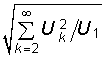и др.

Для синусоидального сигнала k_ф = /21,11; k_a = 1,41; k_и = 1; k_г = 0.

5.3. Спектры периодических негармонических сигналов

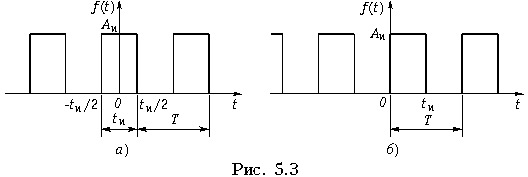
Рассмотрим последовательность прямоугольных импульсов, изображенную на рис. 5.3, а. Сигналы подобной формы находят очень широкое применение в радиотехнике и электросвязи: телеграфия, цифровые системы передачи, системы многоканальной связи с временным разделением каналов, различные импульсные и цифровые устройства и др. (см. гл. 19). Импульсная последовательность характеризуется следующими основными параметрами: амплитудой импульса A_и , его длительностью t_и и периодом следования Т. Отношение периода Т к длительности t_и называется скважностью импульсов и обозначается через q = T/t_и. Обычно значения скважности импульсов лежат в пределах от нескольких единиц (в измерительной технике, устройствах дискретной передачи и обработки информации), до нескольких сотен или тысяч (в радиолокации).

Для нахождения спектра последовательности прямоугольных импульсов воспользуемся рядом Фурье в комплексной форме (5.6). Комплексная амплитуда k-й гармоники равна согласно (5.8) после возвращения к исходной переменной t.

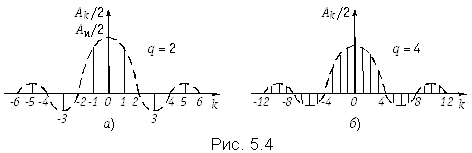
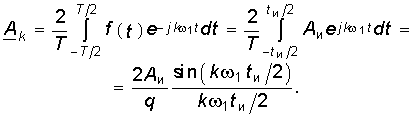   (5.27)

Подставив значение A_k в уравнение (5.6), получим разложение в ряд Фурье: 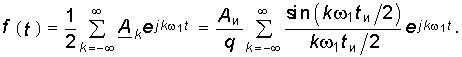   (5.28)

На рис. 5.4 изображен спектр комплексных амплитуд для q = 2 и q = 4. Как видно из рисунка, спектр последовательности прямоугольных импульсов представляет собой дискретный спектр с огибающей (штриховая линия на рис. 5.4), которая описывается функцией    (5.29) носящей название функции отсчетов (см. гл. 19). Число спектральных линий между началом отсчета по оси частот и первым нулем огибающей равно q—1. Постоянная составляющая сигнала (среднее значение) , а действующее значение A = , т.е. чем больше скважность, тем меньше уровень постоянной составляющей и действующее значение сигнала. С увеличением скважности q число дискретных составляющих увеличивается — спектр становится гуще (см. рис. 5.4, б), и амплитуда гармоник убывает медленнее. Следует подчеркнуть, что в соответствии с (5.27) спектр рассматриваемой последовательности прямоугольных импульсов вещественный.

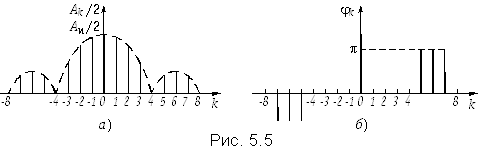
Из спектра комплексных амплитуд (5.27) можно выделить амплитудный A_k = |A_k| и фазовый спектр _k = argA_k, изображенный на рис. 5.5 для случая q = 4. Из рисунков видно, что амплитудный спектр является четной, а фазовый — нечетной функцией частоты. Причем, фазы отдельных гармоник принимают либо нулевое значение между узлами, где синус положительный, либо ±, где синус отрицательный (рис. 5.5, б)

На основании формулы (5.28) получим тригонометрическую форму разложения в ряд Фурье по четным гармоникам (сравни с (5.15)): 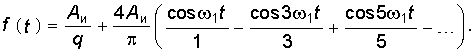   (5.30)

При сдвиге импульсной последовательности по оси времени (рис. 5.2, б) в соответствии с (5.13) ее амплитудный спектр останется прежним, а фазовый спектр изменится: 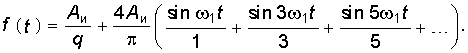   (5.31)

В случае, когда периодическая последовательность имеет разнополярную форму (см. рис. 5.1), в спектре будет отсутствовать постоянная составляющая (сравните (5.30) и (5.31) с (5.14) и (5.15)).

Аналогичным образом можно исследовать спектральный состав периодических негармонических сигналов другой формы. В табл.5.1 приведено разложение в ряд Фурье некоторых наиболее распространенных сигналов.

Таблица 5.1

	Типы сигнала	Разложение в ряд Фурье
1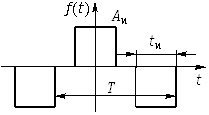
2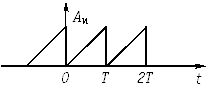
3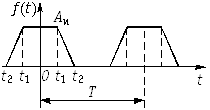
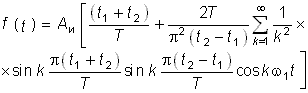4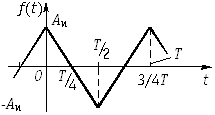
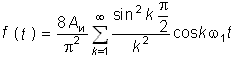5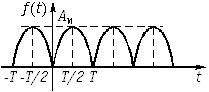
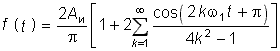6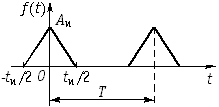

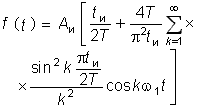5.4. Расчет цепей при периодических негармонических воздействиях

В основе расчета линейных электрических цепей, находящихся под воздействием периодических негармонических сигналов, лежит принцип наложения. Его суть применительно к негармоническим воздействиям заключается в разложении негармонического периодического сигнала в одну из форм ряда Фурье (см. 5.1. Негармонические периодические сигналы. Разложение в ряд Фурье) и определении реакции цепи от каждой гармоники в отдельности. Результирующая реакция находится путем суперпозиции (наложения) полученных частичных реакций. Таким образом, расчет цепей при периодических негармонических воздействиях включает в себя задачу анализа спектрального состава сигнала (разложение его в ряд Фурье), расчет цепи от каждой гармонической составляющей и задачу синтеза, в результате которого определяется результирующий выходной сигнал как функция времени (частоты) или его действующее (амплитудное значение).

При решении задачи анализа обычно пользуются тригонометрической (5.3) или комплексной (5.6) формой ряда Фурье с ограниченным числом членов разложения, что приводит к некоторой погрешности аппроксимации истинного сигнала. Коэффициенты разложения a_k и b_k в (5.3) или A_k и _k в (5.6) определяются с помощью уравнений (5.4), (5.7) и (5.8). При этом входной сигнал f(a) должен быть задан аналитически. В случае, если сигнал задается графически, например в виде осциллограммы, то для нахождения коэффициентов разложения a_k и b_k можно использовать графоаналитический метод (см. (5.16)).

Расчет цепи от отдельных гармоник ведется обычно символическим методом. При этом необходимо иметь в виду, что на k-й гармонике индуктивное сопротивление X_L(k) = kL, а емкостное сопротивление X_C(k) = 1/(kС), т. е. на k-й гармонике индуктивное сопротивление в k раз больше, а емкостное в k раз меньше, чем на первой гармонике. Этим в частности объясняется то обстоятельство, что высокие гармоники в емкости выражены сильнее, а в индуктивности слабее, чем в приложенном к ним напряжении. Активное сопротивление R на низких и средних частотах можно считать не зависящим от частоты.

После определения искомых токов и напряжений от отдельных гармоник методом наложения находят результирующую реакцию цепи на негармоническое периодическое воздействие. При этом либо определяют мгновенное значение результирующего сигнала на основании расчета амплитуд и фаз отдельных гармоник, либо его амплитудные или действующие значения согласно уравнениям (5.18), (5.19). При определении результирующей реакции необходимо помнить, что в соответствии с представлением периодических негармонических колебаний на комплексной плоскости векторы различных гармоник вращаются с различной угловой частотой.

Пример. К цепи, изображенной на рис. 5.6, приложено напряжение u(t) в форме прямоугольных импульсов с периодом повторения T = 2t_и и амплитудой A_и = 1В (см. рис. 5.3, б). Определить мгновенное и действующее значения напряжения на емкости.

Разложение данного напряжения в ряд Фурье определяется по формуле (5.31). Ограничимся первыми тремя членами разложения (5.31):

Таким образом, приложенное напряжение содержит постоянную составляющую U₀ = 1/2, первую U₁ = 4/ и третью U₃ = 4/(3) гармоники с нулевыми начальными фазами. Найдем напряжение на емкости от постоянной составляющей приложенного напряжения U₀: .

Комплексное действующее напряжение от первой гармоники

Токи I₂₍₁₎ или I₃₍₁₎ можно найти по формуле разброса. Например, для I₃₍₁₎ имеем:

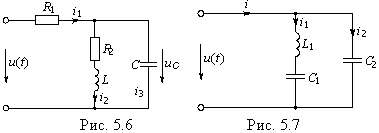
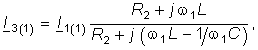где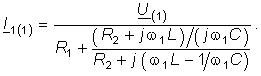

Аналогичным образом находится напряжение на емкости от 3-й гармоники: где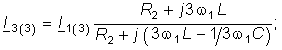

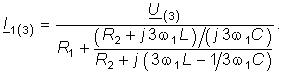
После нахождения комплексных действующих значений напряжений на емкости отдельных гармоник и выделения в них модулей U_C(1), U_C(3) и фаз _C1 = arg U_C(1), _C3 = arg U_C(3) записывает мгновенное значение напряжения на емкости в форме суммы (ряда): .

Действующее значение напряжения определяем согласно (5.19)

При анализе резонансных явлений в электрических цепях при периодических несинусоидальных воздействиях следует иметь в виду, что резонанс напряжений и токов может достигаться на разных гармониках. При этом, как и ранее, резонансом на k-й гармонике называется такое состояние электрической цепи, состоящей из разнохарактерных реактивных элементов, при котором фазовый сдвиг между входным током и приложенным напряжением k-x гармоник равен нулю. Явление резонанса может быть использовано для выделения отдельных гармоник из периодического несинусоидального сигнала. Следует подчеркнуть, что в цепи может одновременно быть достигнут резонанс токов на одной частоте и резонанс напряжений на другой.

Пример. Для цепи, изображенной на рис. 5.7, при заданной ₁, L₁ найти значение C₁ и C₂, при которых одновременно возникает резонанс напряжений на 1-й и резонанс токов на 5-й гармонике.

Из условия резонанса напряжений находим, что входное реактивное сопротивление цепи на первой гармонике должно равняться нулю: 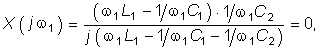   (5.32)

а на пятой — бесконечности (входная реактивная проводимость на пятой гармонике должна быть равна нулю): 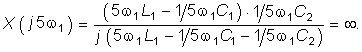   (5.33)

Из условий (5.32) и (5.33) находим искомое значение емкостей:

5.5. Вопросы и задания для самопроверки

1. Какова математическая модель спектра периодического несинусоидального сигнала?
2. Какой вид имеет спектр периодического негармонического сигнала?
3. Как изменяется спектр периодического негармонического сигнала при сдвиге начала отсчета заданной функции?
4. Как определить спектр периодической функции, заданной графически?
5. Как определяется средняя за период активная мощность периодического негармонического сигнала?
6. Как определяется и что характеризует мощность искажений?
7. Как рассчитывается спектр комплексных амплитуд последовательности прямоугольных импульсов?
8. Как влияет скважность импульсов на спектр сигнала?
9. Рассчитать и построить спектр амплитуд последовательности прямоугольных импульсов с параметрами: U_m = 3В, f = 0,5 кГц для двух случаев (q = 2, q = 5).

   Ответ: 1) q = 2; U₀ = 3 В; U_m1 = 1,9 В; U_m2 = 0; U_m3 = 0,64 В;U_m4 = 0; U_m5 = 0,38 В; U_m6 = 0.

   2) q = 5; U₀ = 1,2 В; U_m1 = 1,1 В; U_m2 = 0,91 В; U_m3 = 0,6 В; U_m4 = 0,28 В; U_m5 = 0; U_m6 = 0,19 В; U_m7 = 0,25 В; U_m8 = 0,23 В; U_m9 = 0,12 В; U_m10 = 0.

10. Каков алгоритм расчета линейных электрических цепей, находящихся под воздействием периодических негармонических сигналов?
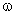11. На вход цепи, изображенной на рис. 5.8, поступает периодический негармонический сигнал u(t) = U₀ + U_m1sin₁t + U_m3sin(3₁t + 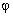₃); U₀ = 30 В; U_m1 = 100 В; U_m3 = 40 В; 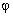₃ = 20°. Параметры элементов цепи на основной частоте известны: 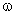₁L = 12 Ом; 1/(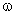₁С) = 30 Ом; R₁ = 6 Ом; R₂ = 5 Ом; R₃ = 20 Ом. Рассчитать: 1) ток в неразветвленной части схемы и записать его мгновенное значение; 2) действующие значения всех токов; 3) активную мощность, потребляемую цепью.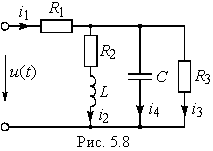

    Ответ: 1) i₁(t) = 3 + 5,88sin(₁t – 16° 30' ) + 2,6sin(3₁t + 55°), A. 2) I₁ = 5,45 А; I₂ = 4,4 А; I₃ = 2,64 А; I₄ = 2,57 А. 3) P = 415 Вт.

12. Резонансные явления в линейных электрических цепях при негармонических периодических воздействиях.
13. Для цепи изображенной на рис. 5.7, найти значения С₁ и С₂, при которых одновременно возникает резонанс напряжений на 1-ой гармонике и резонанс токов на 5-ой гармонике, если заданы L₁ = 10 мГн; ₁ = 5×10³ рад/с.

    Ответ: С₁ = 4 мкФ; С₂ = 0,167 мкФ.