3.1. Теорема Котельникова

3.2. Спектр дискретного сигнала

3.3. Аналого-цифровое и цифро-аналоговое преобразование сигналов

3.1. Теорема Котельникова

Передача непрерывных (аналоговых) сигналов по линии связи предполагает передачу бесконечного множества их мгновенных значений на протяжении конечного промежутка времени. При этом спектр финитного, т.е. ограниченного во времени, непрерывного сигнала бесконечен. Однако, на практике различные радиотехнические устройства (фильтры, усилители и другие) имеют ограниченную полосу пропускания, что приводит к ограничению спектра сигнала некоторой граничной частотой  (или ), которая определяется свойствами получателя сообщений. Так например, общепринятой нормой в системах передачи речевых сигналов является ограничение спектра сигнала в пределах , в системах телевидения – . Как преодолеть противоречие между ограничением спектра сигнала и конечным временем его существования? Ответ на этот вопрос даёт теорема, сформулированная и доказанная академиком В.А. Котельниковым и получившая название теоремы Котельникова или теоремы отсчётов.

Теорема Котельникова формулируется следующим образом. Непрерывный сигнал , ограниченный по спектру частотой  (или), полностью определяется совокупностью мгновенных значений (отсчётов)  в моменты времени , отстоящие друг от друга на интервал времени  .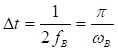

Математически теорема Котельникова определяется выражением

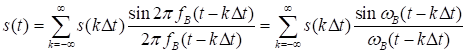,         (3.1)

или с учётом (2.12)

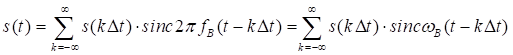,     (3.2)

которое представляет собой разложение сигнала  в особого рода ряд по системе базисных функций

,

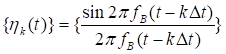являющихся ортогональными на интервале времени  (сравните с разложением сигнала в ряд Фурье).

Доказательство теоремы Котельникова приведено в литературе  [1]. Мы же остановимся на вопросах физического толкования и практического применения результатов теоремы.

Выделим одно из слагаемых ряда (3.1)

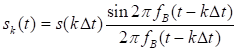.                            3.3)

Это слагаемое представляет собой отклик идеального фильтра нижних частот (ФНЧ), т.е. фильтра с постоянным коэффициентом передачи в пределах полосы частот от нуля до , на очень короткий импульс с амплитудой . (рис. 3.1).

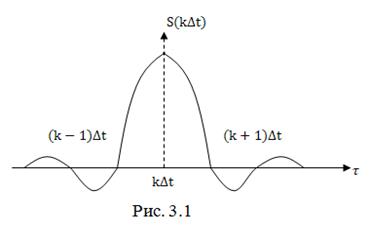
Отметим, что в моменты времени ,  и т.д. значения отклика равны нулю. Это определяет механизм восстановления непрерывного сигнала по его отсчётам.

Формирование последовательности отсчётов непрерывного сигнала, которая представляет собой дискретный сигнал, т.к. значение любого отсчёта  сохраняется неизменным в течение интервала времени  (см. классификацию сигналов), осуществляется при помощи импульсного модулятора.

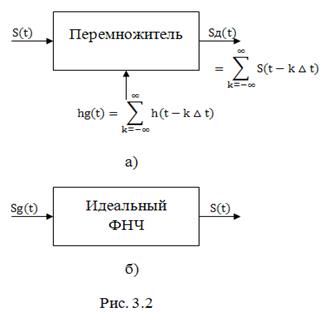Простейший вариант импульсного модулятора представляет со­бой перемножитель (рис. 3.2), на один вход которого подаётся непре­рывный сигнал , а на второй – последовательность

коротких единичных импульсов вида (1.13), следующих друг за другом с периодом  (рис. 3.2, а). Тогда на выходе перемножителя будет иметь место последовательность коротких импульсов

,

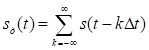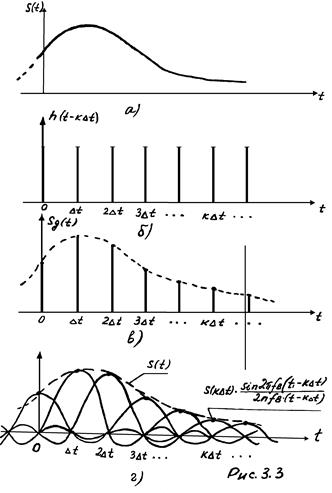амплитуды которых равны , т.е. соответствуют мгновенным значениям сигнала , отсчитанным в момент времени . (рис 3.3, в).

Процесс формирований последовательности отсчётов называется дискретизацией непрерывного сигнала.

Восстановление непрерывного сигнала осуществляется путём подачи дискретного сигнала  на идеальный фильтр нижних частот. Отклик фильтра на каждый отсчёт определяется выражением (3.2). При этом, в момент времени , значение отклика определяется только k -тым отсчётом дискретного сигнала; отклик на остальные отсчёты равны нулю (Рис. 3.3, г). Суммируясь, эти отклики дают на выходе ФНЧ исходный сигнал .

Отметим два важных обстоятельства.

Во-первых, точное восстановление сигнала имеет место только при 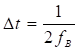. Введя в рассмотрение частоту дискретизации , получим так называемую частоту Найквиста, т.е. минимальное значение частоты дискретизации, при котором возможно точное восстановление непрерывного сигнала. Обычно, на практике частоту дискретизации выбирают выше предела Найквиста. Так, например, частота Найквиста для речевого сигнала при  составляет . В реальных РТИС эта частота составляет .

Во-вторых, точное восстановление сигнала возможно при суммировании бесконечного числа откликов, что соответствует сигналу , неограниченному во времени. Но в действительности, сигналы являются ограниченными и по спектру и по времени. Однако, при определённых допущениях теорема Котельникова справедлива и для этого случая.

Если сигнал, длительностью  ограничивается радиотехническим устройством с граничной частотой , то для его представления в дискретной форме требуется конечное число  отсчетов, где

.                               (3.4)

Таким образом для восстановления сигнала длительностью , ограниченного по спектру частотой  достаточно передать  независимых отсчетов, однозначно связанных с его формой.

Но теоретически сигнал, ограниченный по времени имеет бесконечный спектр. А это означает, что при восстановлении сигнала по  отсчетам будет иметь место ошибка, т.е. восстановленный сигнал ŝ(t) будет отличаться от исходного . Казалось бы, теорема Котельникова неприменима к реальным сигналам. Тем не менее, если к точности восстановления сигнала  по  отсчетам предъявить определенные требования, например, допустить его восстановление с заданным уровнем ошибки, то утверждения теоремы Котельникова можно с успехом распространить на реальные сигналы, несколько изменив частоту дискретизации по сравнению с пределом Найквиста.

Теперь с учетом того, что реальный сигнал длительностью  представляется  отсчетами мгновенных значений, выражение (3.1) принимает вид:

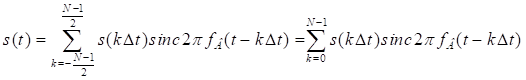.    (3.5)

Величина  называется базой сигнала . Понятие базы играет важную роль при представлении непрерывного сигнала конечным числом отсчетов. Соответствующим образом выбранная база определяет информационные показатели сигналов, способность противостоять помехам при передаче по каналам связи, энергетическую скрытность и другие.

Рассмотрим теперь вопрос оценки точности восстановления непрерывного сигнала по совокупности  отсчетов его мгновенных значений. Как уже неоднократно подчеркивалось выше, ограниченный во времени сигнал имеет бесконечный спектр. Согласно равенству Парсеваля (2.50) энергия такого сигнала равна

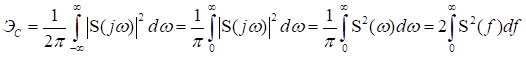,    3.6)

где         или  – энергетический спектр, представленный как функция либо круговой , либо циклической  частоты.

Энергия за пределами частоты (или ) составляет величину

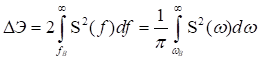.                        (3.7)

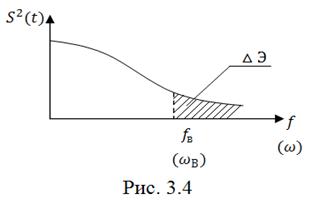
На рис. 3.4 изображен энергетический спектр сигнала, ограниченного во времени и граничная частота .

Площадь под всей кривой характеризует полную энергию сигнала , а площадь заштрихованного участка - ту часть энергии , которая сосредоточена за пределами .

Тогда отношение

               (3.8)

может  служить  оценкой точности восстановления сигнала. Задаваясь величиной  можно определить частоту , а следовательно и частоту дискретизации .

Рассмотрим следующий пример. Пусть сигнал  на интервале времени  описывается экспоненциальной функцией

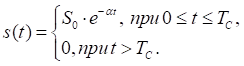
Воспользовавшись преобразованием Фурье, найдем спектральную функцию сигнала

.

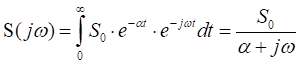Модуль спектральной функции

,

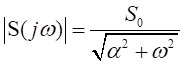а энергетический спектр

.

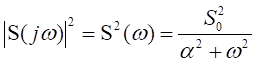Воспользовавшись выражением (3.5), найдем энергию сигнала

.

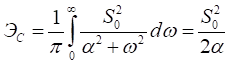В соответствии с (3.6), вычислим :

.

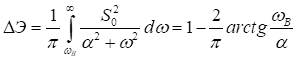При расчете  и  использован табличный интеграл

.

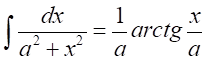Найдем величину среднеквадратичной ошибки восстановления

.

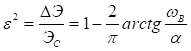Представим

.

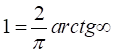Тогда

,

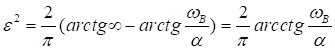откуда следует

.

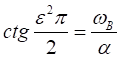Полагая, что для малых значений

,

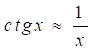получим

.

Теперь можно найти

,

или переходя к циклическим частотам

.

Частота дискретизации

.

Таким образом, задаваясь величиной  можно определить частоту дискретизации непрерывного сигнала. Очевидно, число отсчетов при дискретизации рассматриваемого сигнала будет равно

.

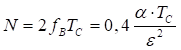Из приведенного примера следует, что чем меньшую ошибку восстановления требуется обеспечить, тем выше должна быть частота дискретизации.

Теорема Котельникова устанавливает однозначное соответствие между аналоговым сигналом и отсчетами его мгновенных значений во временной области. Оказывается, можно сформулировать теорему отсчетов и в частотной области. При этом примем во внимание, что комплексный спектр одиночного сигнала длительностью  является сплошным. Тогда имеет место следующее утверждение. Спектральная функция  сигнала , ограниченного во времени величиной  полностью определяется совокупностью отсчетов , отстоящих друг от друга на частотный интервал 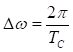, т.е.

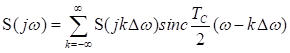.                     (3.9)

Теорема отсчетов в частотной области основывается на свойстве симметрий преобразований Фурье относительно переменных (или ) и . Суть этого свойства состоит в том, что преобразование Фурье периодического сигнала с периодом  приводит к линейчатой (дискретной) спектральной функции, где отдельные спектральные составляющие (см. подраздел 2.1) отстоят друг от друга по оси частот на величину  (или ), и наоборот, преобразование Фурье периодической спектральной функции с периодом  приводит к дискретной временной функции с периодом .

Исходя из этого свойства, если в (3.2) заменить  на ;  на , а  на , то в результате получим выражение (3.9). Как и в случае разложения сигнала  в ряд Котельникова, разложение его спектра ограничивается  отсчетами. Тогда выражение (3.5) в частотной области принимает вид

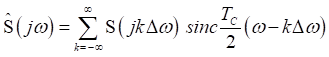.             (3.10)

Казалось бы, для восстановления спектральной функции  по совокупности отсчетов , необходимо знать  отсчетов модуля и  отсчетов аргумента комплексных величин . Однако, если учесть, что модуль спектра , т.е. амплитудный спектр является четной функцией, а аргумент , т.е. фазовый спектр – нечетной функцией, то число независимых отсчетов сокращается вдвое и составляет , т.е. равно базе сигнала.

Подводя итог вышеизложенному, отметим, что теорема Котельникова устанавливает принципиальную возможность представления непрерывного сигнала последовательностью его мгновенных значений. Такую операцию иногда называют импульсным преобразованием непрерывного сигнала. Такое преобразование лежит в основе импульсных методов передачи сообщений в радиотехнических системах. Более того, дискретизация непрерывных сигналов в соответствии с теоремой Котельникова является промежуточной операцией при формировании цифровых сигналов, которые в настоящее время нашли самое широкое распространение как в радиотехнических системах передачи сообщений, так и радиоэлектронных системах обработки, отображения и регистрации информации, и во многих других областях.

3.2. Спектр дискретного сигнала

Перейдем теперь к рассмотрению спектра дискретного сигнала. Очевидно, в соответствии с изложенным выше свойством симметрии преобразования Фурье следует ожидать периодического характера спектральной функции дискретного сигнала.

Итак, дискретный сигнал , как уже подчеркивалось выше, формируется на выходе перемножителя, на один вход которого, подается непрерывный сигнал , а на второй – периодическая последовательность коротких импульсов длительностью

,

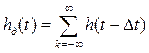с периодом .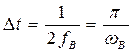

Здесь – функция, определяющая форму импульсов периодической последовательности. Обычно в качестве периодической последовательности импульсов дискретизации выбирают импульсы прямоугольной формы вида (1.13). Периодическую последовательность импульсов дискретизации можно описать выражением

.

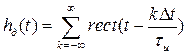Тогда дискретный сигнал запишется в виде

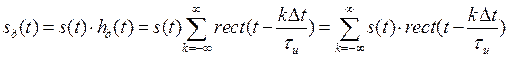. (3.11)

С другой стороны, последовательность прямоугольных импульсов может быть представлена комплексным рядом Фурье

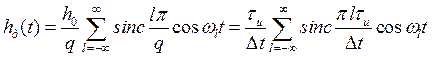. (3.12)

Здесь учтено, что период последовательности равен , амплитуда единичного импульса , а также .

Теперь можно представить с учетом (3.12) в виде ряда

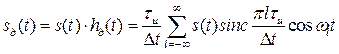. (3.13)

Применим к (3.13) прямое преобразование Фурье

.

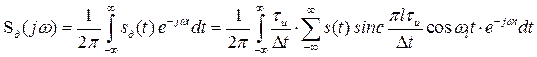Изменив порядок суммирования и интегрирования, запишем

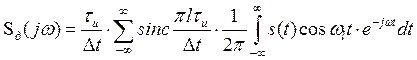. (3.14)

Так как

,

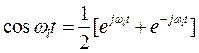то

.

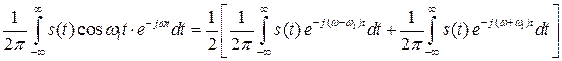В свою очередь

,

.

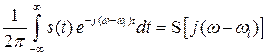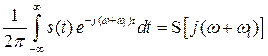Тогда окончательно выражение (3.14) принимает вид

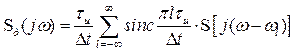. (3.15)

Спектральный анализ дискретного сигнала существенно упрощается, если предположить, что дискретизация осуществляется последовательностью прямоугольных импульсов единичной площади. В этом случае амплитуда импульса 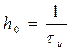и выражение (3.15) запишется следующим образом

.

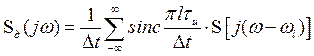Если устремить к нулю при сохранении единичной площади импульса и перейти к последовательности бесконечно коротких импульсов ( -импульсов), т.е.

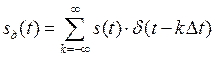, (3.16)

то

,

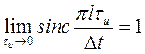а спектральная функция дискретного сигнала примет вид

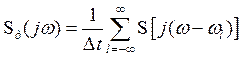. (3.17)

На рис. 3.5, а представлен непрерывный сигнал , а на рис. 3.5, б – условное изображения модуля его спектральной функции .

Как известно, спектр непрерывного одиночного сигнала является сплошным.

Спектр же дискретного сигнала, как это следует из (3.16), представляет собой периодическую по частоте последовательность копий спектров исходного сигнала, сдвинутых относительно друг друга на величину (или ), что составляет период последовательности. Очевидно, периодическим по частоте с тем же периодом является и модуль спектра и его аргумент, т.е. фазовый спектр.

Отметим, что (или ) – это частота дискретизации. Таким образом, период спектральной функции дискретного сигнала равен частоте дискретизации. На рис. 3.5. в, г изображены графики дискретного сигнала и модуля его спектра.

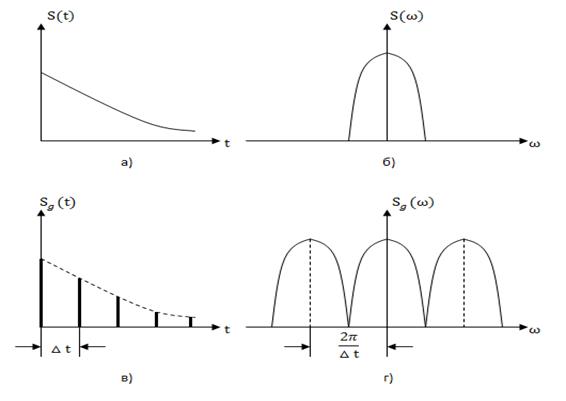
Рис. 3.5

Расположение отдельных составляющих периодической функции спектра дискретного сигнала на оси частот зависит от значения частоты дискретизации . На рис. 3.5,г и на рис. 3.6, а, б изображены соответственно функции дискретного сигнала при частотах дискретизации (или ), (или ) и (или ). Из этих рисунков следует, что при частоте дискретизации, меньшей чем частота, определяемая пределом Найквиста, копии спектра исходного непрерывного сигнала перекрываются, т.е. имеет место явление наложения спектров. Это приводит к искажению исходного сигнала при его восстановлении. Таким образом, и спектральный анализ дискретного сигнала согласуется с выводами теоремы Котельникова.

3.3. Аналого-цифровое и цифро-аналоговое преобразование сигналов

Представление непрерывного сигнала в виде последовательности дискретных отсчётов предполагает, что любой отсчёт может принимать любое значение из непрерывного множества значений . Вместе с тем, цифровые технологии в радиотехнике требуют преобразований совокупности значений отсчётов в цифровую последовательность, т.е. в последовательность чисел. Процесс преобразования аналогового (непрерывного) сигнала в такую последовательность называется аналогово-цифровым преобразованием (АЦП).

Итак, на первом этапе аналогово-цифрового преобразования осуществляется дискретизация непрерывного сигнала, т.е. преобразование в в соответствии с теоремой Котельникова, которая была рассмотрена выше. В результате дискретизации непрерывный (аналоговый) сигнал преобразуется в последовательность отсчётов .

На втором этапе последовательность отсчётов подвергается процедуре квантования по уровню. Квантование по уровню значений отсчётов в простейшем случае представляет собой округление этих значений до ближайшего целого числа. Процедуру квантования осуществляет устройство с амплитудной характеристикой ступенчатого вида, которое называется квантователем. Амплитудная характеристика квантователя изображена на рис. 3.7.

При реализации квантователя диапазон изменения уровня дискретного сигнала разбивается на уровней (включая нулевой), каждый из которых отличается от соседних на величину , называемую шагом квантования.

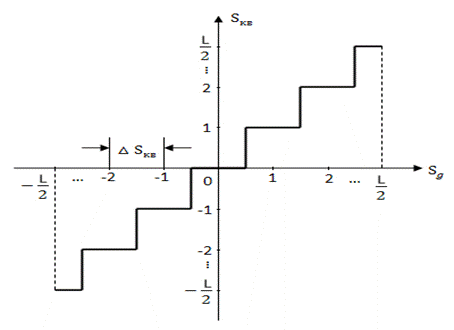
Рис. 3.7

Таким образом, максимальное и минимальное значения квантованного сигнала соответственно равны

, .

В процессе квантования значение в момент времени сравнивается со значением , где . Квантованный сигнал принимает значение

, (3.18)

если

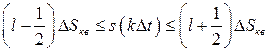. (3.19)

Отметим, что значение запоминается до момента следующего отсчёта дискретного сигнала.

Процедура квантования показана на рис. 3.8.

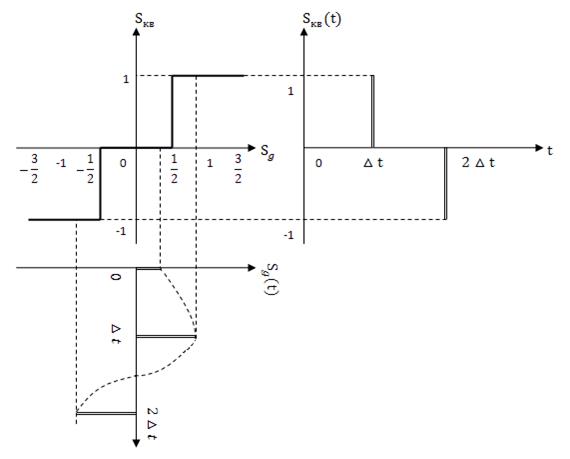
Рис. 3.8

На этом рисунке изображены фрагмент амплитудной характеристики квантователя, дискретный сигнал , временная диаграмма которого повёрнута на для удобства пояснения процедуры квантования, и квантованный сигнал .

Поясним процедуру квантования. Рассмотрим отсчёт . Поскольку значение этого отсчёта находится в интервале , в соответствии с (3.18) значение квантованного сигнала будет равно , т.к. условие (3.19) выполняется при . Значение отсчёта , как это следует из рисунка, находится в пределах , т.е. условие (3.19) выполняется при , поэтому значение квантованного сигнала . И, наконец, значение отсчёта находится в интервале 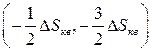, а значение квантованного сигнала .

Ввиду того, что при квантовании осуществляется фактически округление значений , квантованный сигнал будет отличаться от дискретного. При этом искажения, вносимые квантователем

, (3.20)

принципиально неустранимы. Поэтому, при преобразовании непрерывного сигнала в цифровой необходимо оценивать степень искажений, вносимых квантователем.

Искажения, вносимые квантователем, целесообразно оценивать величиной среднеквадратичной ошибки. При исследовании процедур квантования было установлено, что величина среднеквадратичной ошибки

.

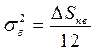Таким образом, ошибка квантования тем меньше, чем меньше шаг квантования .

Физически при преобразовании реальных сигналов проявляется в виде шума. Поэтому искажения получили название шума квантования.

Сигнал на выходе квантователя уже представляет собой цифровой сигнал, однако, представленный в -ичной системе счисления. Напомним, что любое число может быть представлено в системе счисления с основанием следующим образом:

,

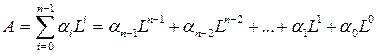где принимает значение из совокупности значений от до ;

– значность числа (количество разрядов, которым представлено число).

Так, например, число в десятичной системе счисления, т.е. при , записывается следующим образом

.

Нетрудно убедится в том, что любое значение на промежутке времени от момента до момента (вспомним замечание о том, что значение запоминается) равно

.

Иными словами, квантованный сигнал представлен одноразрядным числом в -ичной системе счисления. Так как - число уровней квантования, которое выбирается довольно большим, осуществлять передачу и обработку такого сигнала средствами вычислительной техники, которые оперируют в подавляющем большинстве случаев с числами в двоичной системе счисления, неудобно. Поэтому квантованный сигнал, как число, необходимо перевести из - ичной системы в некоторую другую, более удобную с точки зрения дальнейшей передачи и обработки, систему счисления. Эта операция называется кодированием.

Перевод числа из одной системы счисления в другую сопровождается изменением разрядности числа. Соотношение разрядности числа, представленного в системах с основаниями и определяются формулой

.

Поэтому, при переводе числа из системы с основанием в систему с основанием число разрядов будет равно

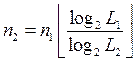, (3.21)

где знак означает округление до ближайшего верхнего целого числа.

Практикой установлено, что для передачи речевого сигнала в цифровой форме необходимо 256 уровней квантования. Эта величина принята в качестве международного стандарта. Значит, при квантовании речевого сигнала значение будет представлено одним разрядом в 256-ричной системе счисления. Для дальнейшей передачи и обработки эти числа обычно переводят в двоичную систему счисления. При этом количество разрядов числа , в соответствии с (3.21), составит

,

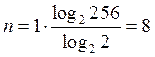а значение каждого разряда может быть или нулем, или единицей.

Таким образом, в результате кодирования квантованный сигнал принимает форму двоичной последовательности, называемой кодовой комбинацией или кодовым словом.

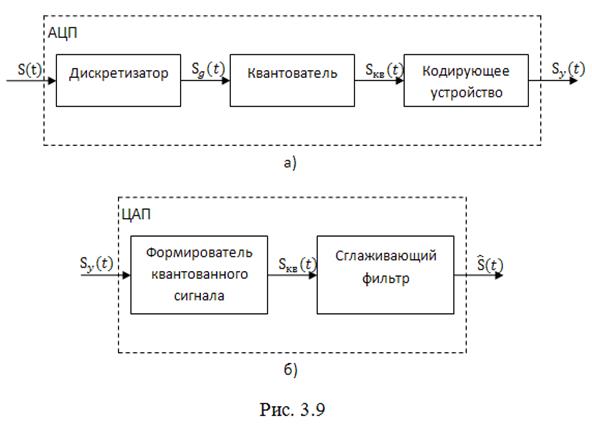
На рис. 3.9 в качестве примера представлен квантованный сигнал при числе уровней квантования и кодовые слова для значений и . Очевидно при в соответствии с (3.21) число разрядов кодового слова составит

.

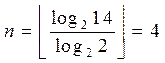Тогда при кодировании значения образуется кодовое слово 1101, а при кодировании кодовое слово 0101.

Отметим, что минимальное значение квантованного сигнала в рассмотренном случае кодируется кодовым словом 0000 .

Если физически разряд кодового слова представлен в виде прямоугольного импульса амплитудой , то двоичный цифровой сигнал будет иметь вид представленный на рис. 3.9, б.

Длительность кодовой комбинации цифрового двоичного сигнала, очевидно должна быть равна т.е. интервалу дискретизации. Отсюда длительность элемента (разряда) кодовой комбинации

.

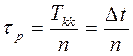Выше было отмечено, что для уменьшения ошибки квантования необходимо уменьшать величину шага квантования . Однако при этом увеличивается число уровней, что в свою очередь приводит к увеличению разрядности кодовой комбинации цифрового сигнала, уменьшению длительности разряда и, следовательно, расширению спектра цифрового сигнала. Это обстоятельство необходимо учитывать при проектировании систем передачи цифровых сигналов по каналам связи.

На практике операции дискретизации, квантования и кодирования осуществляются в одном устройстве называемом аналого-цифровым преобразователем (АЦП). Структурная схема АЦП представлена на рис. 3.9, а. На схеме показаны основные элементы АЦП и сигналы на их входах.

Операция обратного преобразования цифрового сигнала в аналоговый выполняется цифро-аналоговым преобразователем (ЦАП), схема которого представлена на рис. 3.9, б, и предусматривает ряд этапов.

В первую очередь цифровой двоичный сигнал подвергается поразрядному взвешенному (с «весом» ) суммированию, в результате чего в моменты времени формируется квантованный сигнал . После этого последовательность значений квантованного сигнала поступает на сглаживающий фильтр с амплитудно-частной характеристикой

в пределах полосы пропускания или . Как известно из предыдущего материала, при поступлении на вход фильтра сигнала в виде короткого импульса амплитудой , сигнал на выходе будет иметь вид

.

Сложение откликов фильтра дает сигнал ŝ(t). Следует подчеркнуть, что восстановленный сигнал ŝ(t) будет отличатся от исходного ввиду наличия ошибки квантования.