4.3.2. Корреляционный приемник
Полосовая модель процесса обнаружения, рассмотренная в данной главе, практически идентична узкополосной модели, представленной в главе 3. Дело в том, что принятый полосовой сигнал вначале преобразовывается в узкополосный, после чего наступает этап окончательного обнаружения. Для линейных систем математика процесса обнаружения не зависит от смещения частоты. Фактически теорему эквивалентности можно определить следующим образом: выполнение полосовой линейной обработки сигнала с последующим наложением сигнала (превращением полосового сигнала в узкополосный) дает те же результаты, что и наложение сигнала с последующей узкополосной линейной обработкой сигнала. Термин "наложение сигнала" (heterodyning) обозначает преобразование частоты или процесс смешивания, вызывающий смещение спектра сигнала. Как следствие теоремы эквивалентности, любая линейная модель обработки сигналов может использоваться для узкополосных сигналов (что предпочтительнее с точки зрения простоты) с теми же результатами, что и для полосовых сигналов. Это означает, что производительность большинства цифровых систем связи часто можно описать и проанализировать, считая канал передачи узкополосным.
4.3.1. Области решений
Предположим, что двухмерное пространство сигналов, изображенное на рис. 4.6, — это геометрическое место точек, возмущенных шумом двоичных векторов-прототипов ![]() . Вектор шума n — это случайный вектор с нулевым средним; следовательно, вектор принятого сигнала г — это случайный вектор со средним значением s, или s2. Задачей детектора после получения г является принятие решения относительно классификации сигнала, имеющего минимальную вероятность ошибки Pв, хотя возможны и другие стратегии принятия решения [2]. Для случая М = 2 с равновероятными сигналами s1 и s2 и при шуме AWGN (additive white Gaussian noise — аддитивный белый гауссов шум) использование при принятии решения критерия минимума ошибки равносильно такому выбору класса сигнала, чтобы расстояние
. Вектор шума n — это случайный вектор с нулевым средним; следовательно, вектор принятого сигнала г — это случайный вектор со средним значением s, или s2. Задачей детектора после получения г является принятие решения относительно классификации сигнала, имеющего минимальную вероятность ошибки Pв, хотя возможны и другие стратегии принятия решения [2]. Для случая М = 2 с равновероятными сигналами s1 и s2 и при шуме AWGN (additive white Gaussian noise — аддитивный белый гауссов шум) использование при принятии решения критерия минимума ошибки равносильно такому выбору класса сигнала, чтобы расстояние ![]() было минимальным, где ||х|| — норма или абсолютная величина вектора х. Последнее правило часто формулируется в терминах областей решений. Обратимся к рис. 4.6 и рассмотрим формирование областей решений. Итак, вначале необходимо соединить концы векторов-прототипов s1 и s2. Затем через середину полученного отрезка проводится плоскость, перпендикулярная к нему. Отметим, что поскольку амплитуды сигналов s1 и s2 равны, эта плоскость проходит через начало координат и является биссектрисой угла, образованного векторами-прототипами. Эта биссекторная плоскость, изображенная на рис. 4.6 для случая М = 2, является геометрическим местом точек, равноудаленных от векторов s1 и s2; следовательно, она является границей между областью решений 1 и областью решений 2. Правило принятия решения, используемое детектором, формулируется в терминах областей решений следующим образом: если сигнал расположен в области 1 — отнести принятый сигнал к s1; если в области 2 — выбрать сигнал s2. Если угол θ (рис. 4.6) равен 180°, набор сигналов s1 и s2 описывает модуляцию BPSK. Впрочем, для иллюстрации идеи области решений вообще угол θ на рисунке был заведомо выбран меньшим 180°.
было минимальным, где ||х|| — норма или абсолютная величина вектора х. Последнее правило часто формулируется в терминах областей решений. Обратимся к рис. 4.6 и рассмотрим формирование областей решений. Итак, вначале необходимо соединить концы векторов-прототипов s1 и s2. Затем через середину полученного отрезка проводится плоскость, перпендикулярная к нему. Отметим, что поскольку амплитуды сигналов s1 и s2 равны, эта плоскость проходит через начало координат и является биссектрисой угла, образованного векторами-прототипами. Эта биссекторная плоскость, изображенная на рис. 4.6 для случая М = 2, является геометрическим местом точек, равноудаленных от векторов s1 и s2; следовательно, она является границей между областью решений 1 и областью решений 2. Правило принятия решения, используемое детектором, формулируется в терминах областей решений следующим образом: если сигнал расположен в области 1 — отнести принятый сигнал к s1; если в области 2 — выбрать сигнал s2. Если угол θ (рис. 4.6) равен 180°, набор сигналов s1 и s2 описывает модуляцию BPSK. Впрочем, для иллюстрации идеи области решений вообще угол θ на рисунке был заведомо выбран меньшим 180°.
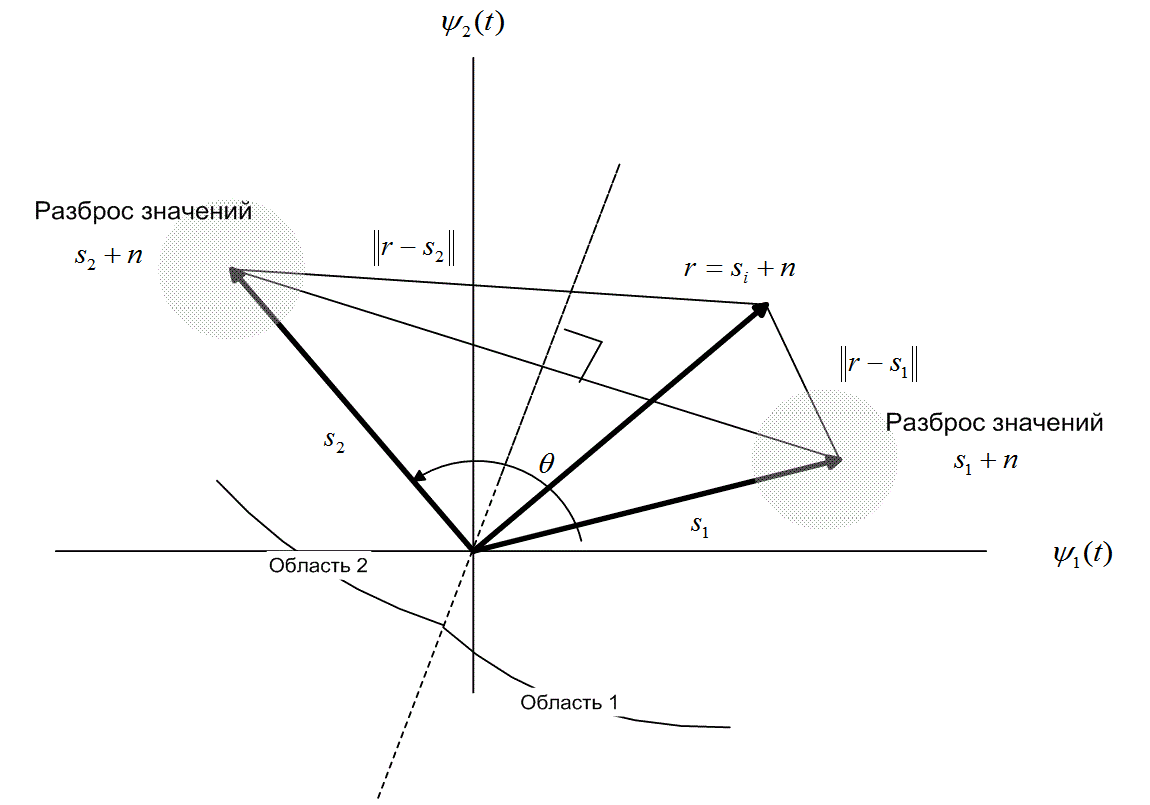
Рис. 4.6. Двухмерное пространство сигналов с равными по модулю произвольными векторами s1 и s2
4.3.2. Корреляционный приемник
В разделе 3.2 было рассмотрено обнаружение узкополосных двоичных сигналов в гауссовом шуме. Поскольку при обнаружении полосовых сигналов используются те же понятия, в данном разделе мы просто обобщим ключевые результаты. Основное внимание будет уделено реализации согласованного фильтра, известного как коррелятор (correlator). Помимо двоичного обнаружения будет рассмотрен более общий случай М-арного обнаружения. Предполагается, что сигнал искажается только вследствие шума AWGN. Принятый сигнал будем описывать как сумму переданного сигнала и случайного шума.
![]() (4.14)
(4.14)
При наличии подобного принятого сигнала процесс обнаружения, как показано на рис. 3.1, включает два основных этапа. На первом этапе принятый сигнал r(t) усекается до одной случайной переменной z(T) или до набора случайных переменных zi(T) (i=1,...,М), формируемых на выходе демодулятора и устройства дискретизации в момент времени t = Т, где Т — длительность символа. На втором этапе на основе сравнения z(T) с порогом или согласно критерию максимума zi(T) принимается решение относительно значения cимвола. Вообще, этап 1 можно рассматривать как преобразование сигнала в точку в пространстве решений. Эту точку, представляющую собой важнейшую контрольную точку в приемнике, можно назвать додетекторной (predetection). Когда мы говорим о мощности принятого сигнала, мощности принятых шумов или отношении еь/nq, все эти величины всегда рассматриваются относительно додетекторной точки. Иногда такие параметры определяются относительно входа приемника или принимающей антенны. Но в подобных случаях всегда подразумевается, что между выбранной и додетекторной точками не происходит снижения отношения сигнал/шум, или Eb/N0. В каждый момент передачи символа сигнал, доступный в додетекторной точке, является выборкой узкополосного импульса. На данный момент битового значения у нас еще нет. Стоит ли удивляться, что отношение энергии бита к N0 определено там, где еще не существует бита? В действительности, нет, поскольку данная точка является удобной контрольной точкой, где узкополосный импульс — даже до принятия решения на битовом уровне — может давать эффективное представление битов. Этап 2 можно рассматривать как определение того, в какой области решений расположена данная точка. Для оптимизации детектора (в смысле минимизации вероятности ошибки) необходимо оптимизировать преобразование сигнала в случайную переменную с использованием согласованных фильтров или корреляторов на этапе 1 и оптимизировать критерий принятия решения на этапе 2.
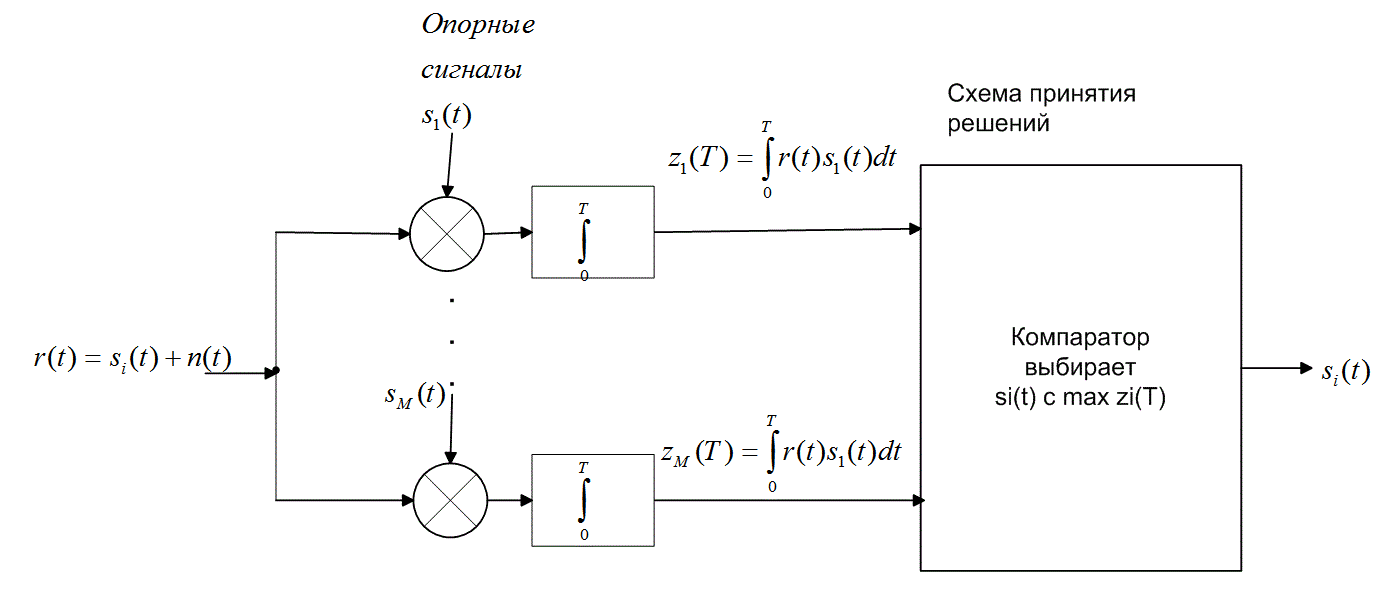
В разделах 3.2.2 и 3.2.3 показывалось, что согласованный фильтр обеспечивает максимальное отношение сигнал/шум на выходе фильтра в момент t = Т. Как одна из реализаций согласованного фильтра описывался коррелятор. Теперь мы можем определить корреляционный приемник (correlation receiver), состоящий, как показано на рис. 4.7, а, из М корреляторов, выполняющих преобразование принятого сигнала r(t) в последовательность М чисел или выходов коррелятора, zi(T) (i=1,...,М). Каждый выход коррелятора описывается следующим интегралом произведения или корреляцией с принятым сигналом.
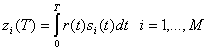 (4.15)
(4.15)
а)
б)
Рис. 4.7. Корреляционный приемник: а) корреляционный приемник с опорными сигналами ![]() ; б) корреляционный приемник с опорными сигналами
; б) корреляционный приемник с опорными сигналами ![]()
Глагол "коррелировать" означает "совпадать", "согласовываться". Корреляторы пытаются найти соответствие принятого сигнала r(t) с каждым возможным сигналом-прототипом si(t), известным приемнику априори. Разумное правило принятия решения звучит так: выбирать сигнал si(t), лучше всего согласующийся, (или имеющий наибольшую корреляцию) с r(t). Другими словами, правило принятия решения выглядит следующим образом.
Выбрать сигнал si(t), индекс которого
Соответствует максимальной zi(T) (4.16)
Следуя формуле (3.10), любой набор сигналов ![]() можно выразить через определенный набор базисных функций
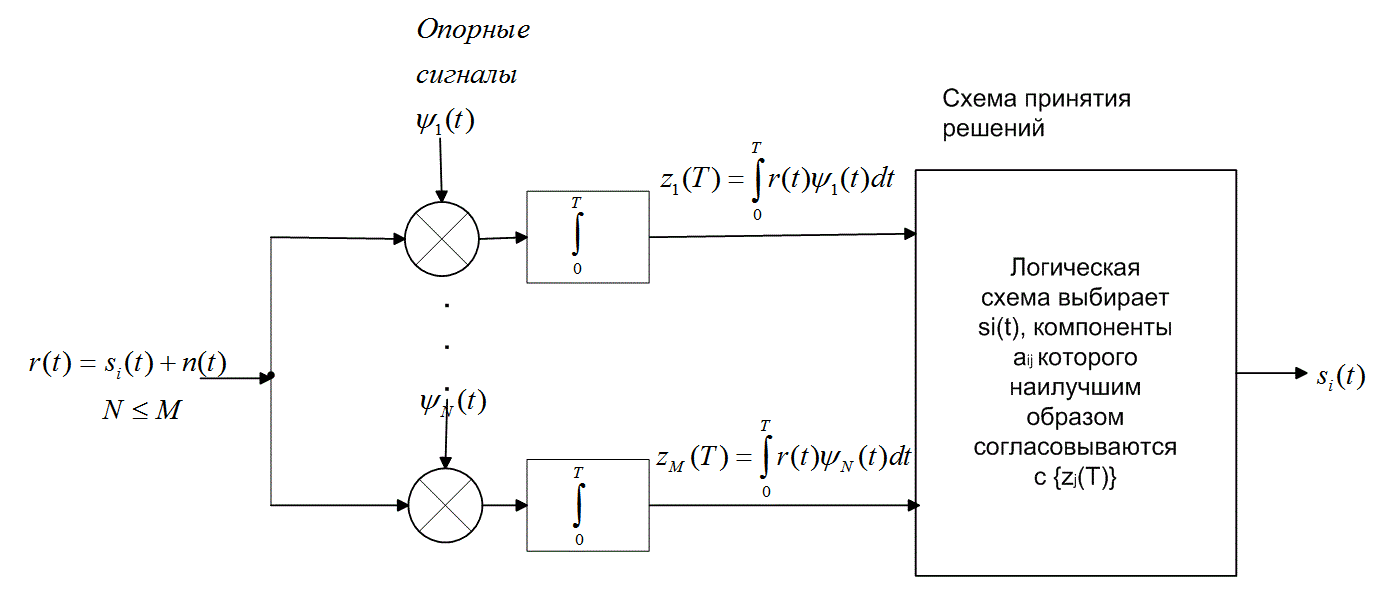
можно выразить через определенный набор базисных функций ![]() . Таким образом, группу из М корреляторов, изображенную на рис. 4.7, а, можно заменить группой из N корреляторов, показанной на рис. 4.7, б, где в качестве опорных сигналов используется набор базисных функций
. Таким образом, группу из М корреляторов, изображенную на рис. 4.7, а, можно заменить группой из N корреляторов, показанной на рис. 4.7, б, где в качестве опорных сигналов используется набор базисных функций ![]() . Для принятия решения с помощью указанных корреляторов необходима логическая схема выбора сигнала si(t) Выбор производится на основе определения наилучшего согласования коэффициентов aij, фигурирующих в формуле (3.10), с набором выходов {zj(T)}. Если набор сигналов-прототипов {s,{t)} формирует ортогональное множество, реализация приемника, показанная на рис. 4.7, а, идентична реализации, показанной на рис. 4.7, б (могут отличаться масштабом). Если же {si(t)} не является ортогональным множеством, приемник (рис. 4.7, б), использующий N корреляторов с опорными сигналами
. Для принятия решения с помощью указанных корреляторов необходима логическая схема выбора сигнала si(t) Выбор производится на основе определения наилучшего согласования коэффициентов aij, фигурирующих в формуле (3.10), с набором выходов {zj(T)}. Если набор сигналов-прототипов {s,{t)} формирует ортогональное множество, реализация приемника, показанная на рис. 4.7, а, идентична реализации, показанной на рис. 4.7, б (могут отличаться масштабом). Если же {si(t)} не является ортогональным множеством, приемник (рис. 4.7, б), использующий N корреляторов с опорными сигналами ![]() вместо М, представляет более рентабельную реализацию. В разделе 4.4.3 мы рассмотрим применение подобного устройства для обнаружения сигнала в модуляции MPSK (multiple phase shift keying — многофазная манипуляция).
вместо М, представляет более рентабельную реализацию. В разделе 4.4.3 мы рассмотрим применение подобного устройства для обнаружения сигнала в модуляции MPSK (multiple phase shift keying — многофазная манипуляция).
В случае двоичного обнаружения корреляционный приемник, как показано на рис. 4.8, а, можно построить как согласованный фильтр или интегратор произведений с опорным сигналом, равным разности двоичных сигналов-прототипов ![]() . Выход коррелятора z(T) используется непосредственно в процессе принятия решения.
. Выход коррелятора z(T) используется непосредственно в процессе принятия решения.
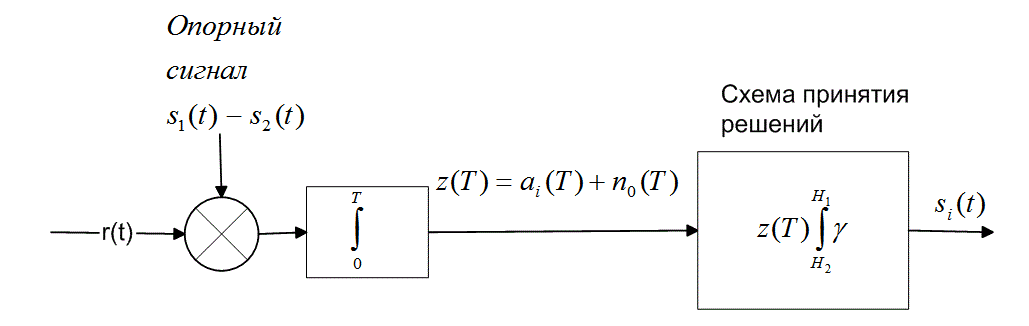
а)
б)
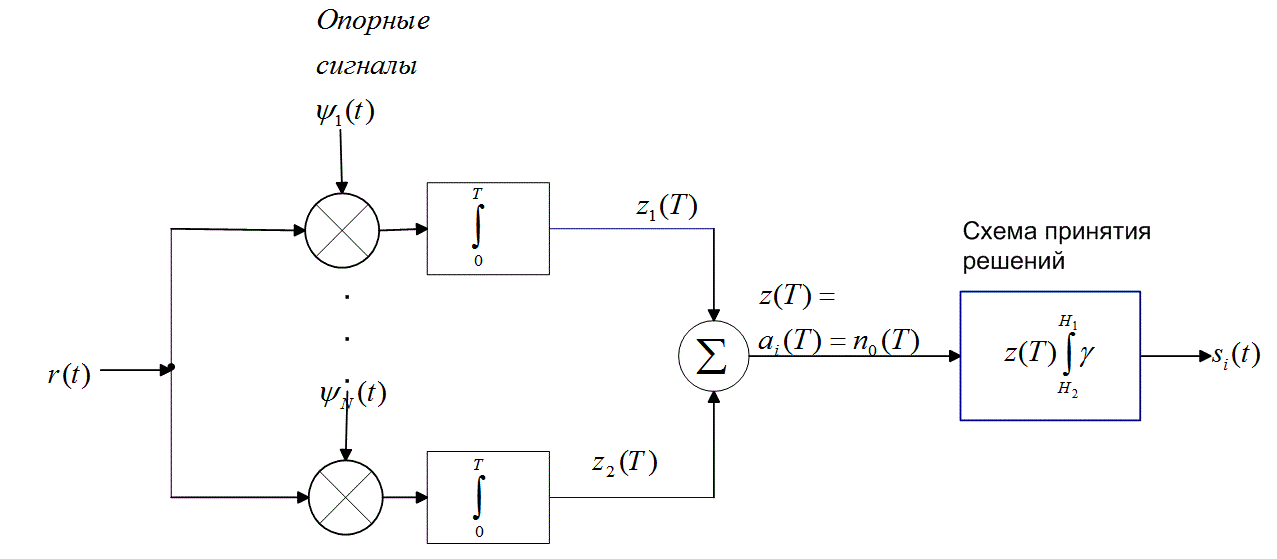
Рис. 4.8. Двоичный корреляционный приемник: а) использование одного коррелятора; б) применение двух корреляторов
При двоичном обнаружении корреляционный приемник можно изобразить как два согласованных фильтра или интегратора произведений, один из которых согласовывается с s1(t), а второй — с s2(t) (рис. 4.8, б). На этапе принятия решения теперь может использоваться правило, приведенное в формуле (6.16), или же из выхода одного коррелятора можно вычесть выход другого и на этапе принятия решения использовать разность
![]() , (4.17)
, (4.17)
как показано на рис. 4.8, б. Здесь z(T), называемое тестовой статистикой (test statistic), подается в схему принятия решения, как и в случае только одного коррелятора. В отсутствие шума на выходе мы получаем z(7) = аi(T), где ai(T) — сигнальный компонент. Входной шум и(7) при этом является случайным гауссовым процессом. Поскольку коррелятор — это линейное устройство, выходной шум является случайным гауссовым процессом [2]. Таким образом, можно записать выражение с выхода коррелятора в момент взятия выборки t = Т:
![]()
где п0(Т) — компонент шума. Для сокращения записи мы иногда будем выражать z(t) как а, + n0. Компонент шума п0 — это гауссова случайная переменная с нулевым средним; следовательно, z(T) — это гауссова случайная переменная со средним a1 или а2в зависимости от того, была передана двоичная единица или двоичный нуль.
4.3.2.1. Порог двоичного решения
На рис. 4.9 для случайной переменной z(T) показаны две плотности условных вероятностей — ![]() и
и ![]() — со средними значениями а1и а2. Эти функции, именуемые правдоподобием s1 и правдоподобием s2, были представлены в разделе 3.1.2. Приведем их повторно.
— со средними значениями а1и а2. Эти функции, именуемые правдоподобием s1 и правдоподобием s2, были представлены в разделе 3.1.2. Приведем их повторно.
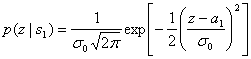 (4.18,а)
(4.18,а)
и
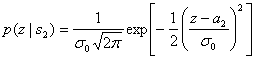 (4.18,б)
(4.18,б)
Здесь ![]() — дисперсия шума. На рис. 4.9 правое правдоподобие
— дисперсия шума. На рис. 4.9 правое правдоподобие ![]() иллюстрирует вероятностное распределение сигналов на выходе детектора z(T) при переданном сигнале s1. Подобным образом левое правдоподобие p(z|s2) демонстрирует вероятностное распределение сигналов на выходе детектор z(T) при переданном сигнале s2. Абсцисса z(T) представляет полный диапазон возможных значений выборок на выходе корреляционного приемника, показанного на рис. 4.8.
иллюстрирует вероятностное распределение сигналов на выходе детектора z(T) при переданном сигнале s1. Подобным образом левое правдоподобие p(z|s2) демонстрирует вероятностное распределение сигналов на выходе детектор z(T) при переданном сигнале s2. Абсцисса z(T) представляет полный диапазон возможных значений выборок на выходе корреляционного приемника, показанного на рис. 4.8.
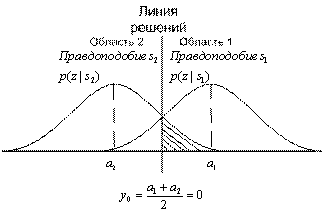
Рис. 4.9. Плотности условных вероятностей ![]() и
и ![]()
При рассмотрении задачи оптимизации порога двоичного решения относительно принадлежности принятого сигнала к одной из двух областей, в разделе 3.2.1 было показано, что критерий минимума ошибки для равновероятных двоичных сигналов, искаженных гауссовым шумом, можно сформулировать следующим образом.
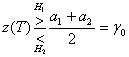 (4.19)
(4.19)
Здесь ![]() — сигнальный компонент z(Т) при передаче s1(t), а
— сигнальный компонент z(Т) при передаче s1(t), а ![]() — сигнальный компонент z(T) при передаче s2(t). Порог γ0, равный (а1 + а2)/2 — это оптимальный порог для минимизации вероятности принятия неверного решения при равновероятных сигналах и симметричных правдоподобиях. Правило принятия решения, приведенное в формуле (4.19), указывает, что гипотеза H1 (решение, что переданный сигнал — это s1(t)) выбирается при z(T)> γ0, а гипотеза Н2(решение, что переданный сигнал — это s2(t)) — при z(T) < γ0. Если z(T) = γ, решение может быть любым. При равновероятных антиподных сигналах с равными энергиями, где s1(t)= -s2(t) и а1 = -а2, оптимальное правило принятия решения принимает следующий вид.
— сигнальный компонент z(T) при передаче s2(t). Порог γ0, равный (а1 + а2)/2 — это оптимальный порог для минимизации вероятности принятия неверного решения при равновероятных сигналах и симметричных правдоподобиях. Правило принятия решения, приведенное в формуле (4.19), указывает, что гипотеза H1 (решение, что переданный сигнал — это s1(t)) выбирается при z(T)> γ0, а гипотеза Н2(решение, что переданный сигнал — это s2(t)) — при z(T) < γ0. Если z(T) = γ, решение может быть любым. При равновероятных антиподных сигналах с равными энергиями, где s1(t)= -s2(t) и а1 = -а2, оптимальное правило принятия решения принимает следующий вид.
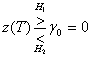 (4.20,а)
(4.20,а)

