12.3.1. Пример схемы прямой последовательности

12.3.2. Коэффициент расширения спектра и производительность

На блок-схеме, приведенной на рис. 12.9, а, изображен модулятор схемы прямой последовательности (direct-sequence — DS). "Прямая последовательность" — это модуляция несущей информационным сигналом x(t) с последующей модуляцией высокоскоростным (широкополосным) расширяющим сигналом g(t). Рассмотрим модулированную данными несущую с постоянной огибающей, которая имеет мощность Р, угловую частоту mo, информационную модуляцию фазы x(t).

(12.7)

После модуляции расширяющим сигналом g(r) с постоянной огибающей переданный сигнал можно представить в следующем виде:

(12.8)

причем фаза несущей теперь состоит из двух компонентов: x(t), который соответствует данным, и g(t), возникший из-за применения расширяющего сигнала.

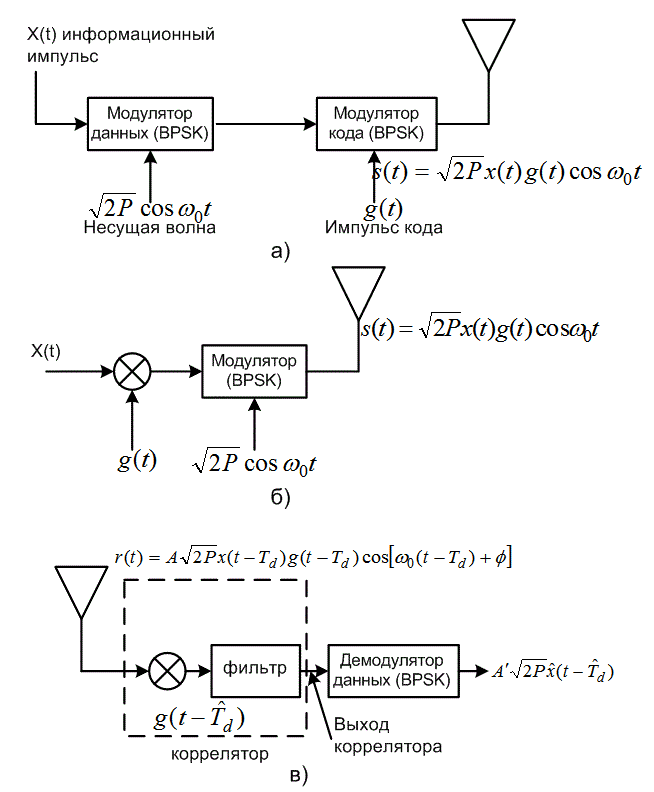
Рис. 12.9. Система расширения спектра методом прямой последовательности: а) передатчик BPSK ; б) упрощенный передатчик BPSK; в) приемник BPSK

В главе 4 было показано, что двоичная фазовая манипуляция (binary phase shift keying — BPSK) с подавлением несущей приводит к мгновенным изменениям фазы несущей на радиан согласно передаваемой информации. Формулу (12.7) также можно записать как произведение несущей и x(t), потока антиподных импульсов со значениями импульсов +1 либо -1.

(12.9)

Если модуляция расширяющей последовательности — это также BPSK, a g(t) — антиподный поток импульсов со значениями импульсов +1 либо -1, уравнение (12.8) может быть представлено в следующем виде.

(12.10)

Модулятор, построенный согласно формуле (12.10), изображен на рис. 12.9, б. Вначале производится перемножение потока импульсных данных и расширяющего сигнала, после чего несущая модулируется полученным сигналом x(t). Если присвоение значений импульсов бинарным значениям выполняется следующим образом

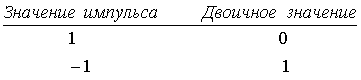
то исходный этап модуляции DS/BPSK может выполняться путем суммирования по модулю 2 двоичной информационной последовательности и двоичной расширяющей последовательности.

Демодуляция сигнала DS/BPSK производится с помощью вычисления корреляции или повторной модуляции принятого сигнала синхронизированной копией расширяющего сигнала (рис. 12.9, в), где — оценка приемником задержки распространения Td между передатчиком и приемником. При отсутствии шумов и интерференции выходной сигнал коррелятора может быть записан следующим образом:

(12.11)

где постоянная А — коэффициент усиления системы, — случайное значение фазового угла из диапазона (0,2). Поскольку g(t)=±1, произведение g(t-Td)g(t-) будет равно единице, если =Td, т.е. если кодовый сигнал в приемнике точно синхронизирован с кодовым сигналом в передатчике. При такой синхронизации выход принимающего коррелятора — это суженный сигнал, модулированный данными (за исключением случайной фазы и времени Td). После этого для восстановления исходных данных используется обычный демодулятор.

12.3.1. Пример схемы прямой последовательности

На рис. 12.10 приводится пример процессов модуляции и демодуляции DS/BPSK, выполняемых в соответствии с блок-схемами рис. 12.9, б и в. На рис. 12.10, а показана двоичная информационная последовательность (1,0) и ее эквивалент в виде биполярного импульсного сигнала x(t). Присвоение двоичных значений импульсам выполняется аналогично случаю, описанному в предыдущем разделе. Примеры двоичной расширяющей последовательности и ее биполярного эквивалента g(t) приводятся на рис. 12.10, б. Результат суммирования по модулю 2 информационной и кодовой последовательностей, а также произведение x(t)g(t) представлены на рис. 12.10, в.

Как показано на рис. 12.10, г, при модуляции BPSK (см. уравнения (12.8) и (12,10)) фаза несущей равна , если произведение сигналов x(t)g(t) равно -1 (или сумма по модулю 2 данных и кода является двоичной единицей). Подобным образом фаза несущей равна нулю, если значение x(t)g(t) равно +1 (или сумма по модулю 2 данных и кода равна двоичному нулю). При сравнении рис. 12.10, б и в легко заметить, что важной особенностью сигналов расширенного спектра является их скрывающее свойство. График на рис. 12.10, в содержит "скрытый" сигнал x(t). Глядя на график, сложно выделить медленно меняющийся информационный сигнал из быстро меняющейся кодовой последовательности. Аналогичная сложность возникает при восстановлении приемником сигнала, если отсутствует точная копия кодового сигнала.

Как видно из рис. 12.10, в, демодуляция DS/BPSK проходит в два этапа. Первый этап — сужение полученного сигнала — выполняется путем определения корреляции этого сигнала с синхронизированной копией кодового сигнала. Второй этап — демодуляция данных — производится с помощью обычного демодулятора. На рис. 12.10, д представлена копия кода g(t) в виде сдвига фазы (0 или ), который осуществляется приемником с целью сужения кода. На рис. 12.10, е представлен процесс вычисления фазы несущей после сужения либо после суммирования g(t) и x(t)+ g(t).

После указанных преобразований исходные данные фактически уже восстановлены и представлены в виде значений фазы несущей. Завершающий этап, показанный на рис. 12.10, ж, предполагает восстановление информационного сигнала с помощью демодулятора BPSK.

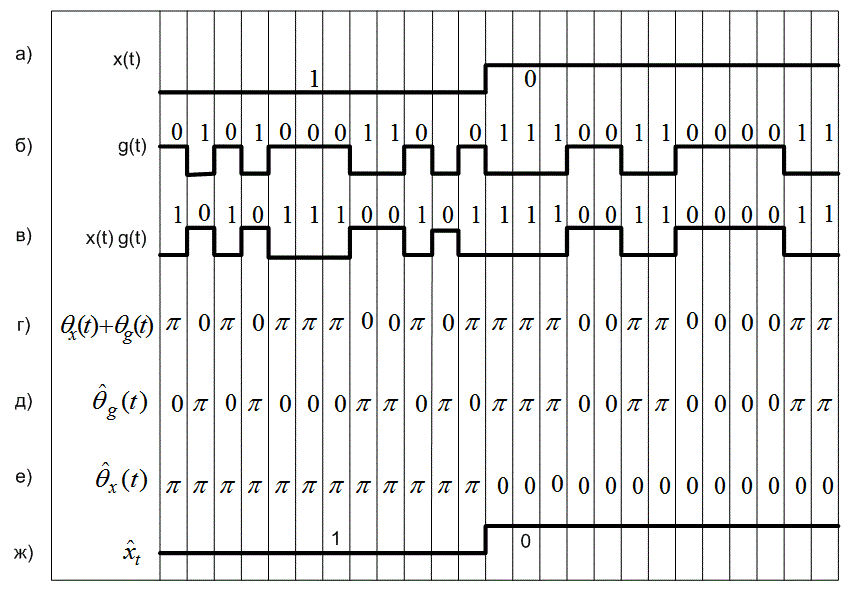
Рис. 12.10. Пример расширения спектра методом прямой последовательности: а) исходные двоичные данные; б) кодовая последовательность; в) переданная последовательность; г) фаза переданной несущей; д) фазовый сдвиг, выполненный кодом приемника; е) фаза принятой несущей после сдвига фаз (сужения); ж) демодулированный информационный сигнал

12.3.2. Коэффициент расширения спектра и производительность

Фундаментальным вопросом в использовании систем расширенного спектра является предлагаемая ими степень защиты сигнала от помех ограниченной мощности. Методы расширения спектра расширяют относительно низкоразмерный сигнал в многомерное сигнальное пространство. Сигнал "скрыт" в этом сигнальном пространстве, поскольку предполагается, что станции-постановщику преднамеренных помех неизвестны координаты передачи сигнала в каждый момент времени. Связь можно нарушить путем создания помех во всем диапазоне, используя при этом всю ограниченную мощность генератора. В этом случае в каждой точке диапазона будут присутствовать помехи ограниченной мощности. Еще одним способом нарушения связи может быть создание помех в некоторых точках диапазона. Соответственно, весь остальной диапазон будет свободен от преднамеренных шумов.

Рассмотрим набор из D ортогональных сигналов si(t), 1<i<D, в N-мерном пространстве. Будем считать, что в общем случае D<<N. В соответствии с выкладками, приведенными в разделе 3.1.3, можно записать следующее.

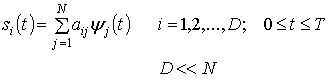(12.12)

где

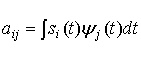(12.13)

а также

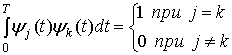(12.14)

Линейно независимые функции охватывают или характеризуют N-мерное ортогональное пространство; их называют базисными функциями пространства. При передаче каждого информационного символа, чтобы скрыть D-мерный сигнал в N-мерном пространстве с помощью псевдослучайного расширяющего кода, независимо выбирается набор коэффициентов {aij}. Набор случайных переменных {aij} может с вероятностью 1/2 иметь значение ±а. Для корректного сужения сигнала приемник, разумеется, должен иметь доступ к каждому набору коэффициентов. Характерно, что даже если передача одного и того жеj-го символа многократно повторяется, набор {aij} выбирается заново для каждого процесса передачи. Предположим, что энергия всех сигналов набора D одинакова. Тогда среднюю энергию сигнала можно записать в следующем виде:

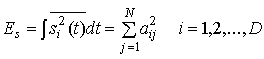(12.15)

где черта над выражением означает математическое ожидание по ансамблю большого числа процессов передачи символов. Независимые коэффициенты имеют нулевое среднее и корреляцию.

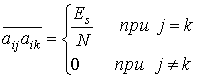(12.16)

Обычно считается, что станция умышленных помех не обладает априорной информацией о наборе коэффициентов {aij}. С точки зрения станции помех коэффициенты равномерно распределены по N базисным координатам. Если помехи создаются равномерно по всему диапазону, сигнал помех w(t) может быть записан в следующем виде.

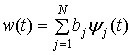(12.17)

Полная энергия такого сигнала равна следующему.

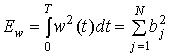(12.18)

Станция умышленных помех может выработать стратегию выбора частей полной (фиксированной) энергии Еw таким образом, чтобы свести к минимуму отношение сигнал/шум (signal-to-noise ratio — SNR) в приемнике после демодуляции.

Выходной сигнал детектора в приемнике

(12.19)

коррелирует с набором переданных сигналов (собственными шумами приемника пренебрегаем), так что выход /-го коррелятора можно записать в следующем виде.

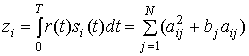(12.20)

Усредненное значение второго члена правой части уравнения (12.20) по ансамблю всех возможных псевдослучайных кодовых последовательностей равно нулю, поскольку считается, что элементы множества случайных переменных {aij} с вероятностью 1/2 принимают значения ± а. Следовательно, если считать, что передан был сигнал sm(t), математическое ожидание выхода i-го коррелятора может быть записано в следующем виде [6, 7].

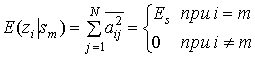(12.21)

Для случая i=m член E(zi|sm) можно интерпретировать следующим образом. Пусть требуется передать сигнал si{t). Выбирается N псевдослучайных коэффициентов аij (1jN). При этом считается, что при восстановлении исходных данных приемник имеет Доступ к каждому набору aij. Таким образом, хотя при вычислении E(zi|sm) i-й информационный символ задается в передатчике, передается набор коэффициентов, которые кажутся случайными для постороннего приемника. Отметим, что в уравнении (12.21) не учитывается возможность использования станцией умышленных помех изощренных, усложненных методов (описанных в разделе 12.6).

Предположим, что D сигналов равновероятны. Тогда математическое ожидание для выхода любого из D корреляторов можно записать следующим образом.

(12.22)

Подобным образом с помощью уравнений (12.15)-(12.21) вычисляем , дисперсию выхода i-го коррелятора, считая что передан i-й сигнал.

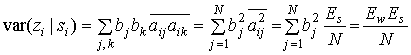(12.23)

(12.24)

Для полноты рассмотрения можно подобным образом вычислить дисперсию выхода i-го коррелятора после передачи m-го сигнала ().

(12.25)

Отношение мощности сигнала к мощности преднамеренной помехи (signal-to-jammer ratio — SJR) на выходе i-го коррелятора может быть определено следующим образом.

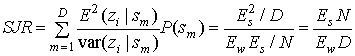(12.26)

Поскольку считается, что вероятность передачи каждого из сигналов одинакова, вероятность передачи т-го сигнала P(Sm) равна 1/D. Энергия сигнала и помехи обозначается, соответственно, E²(zi) и var(zi). В соответствии с уравнением (12.21) члены суммы в (12.26) не равны нулю только при i=m. Таким образом, результат не зависит от распределения энергии станции умышленных помех. Какими бы ни были коэффициенты bj в сумме , значение SJR в уравнении (12.26) свидетельствует о том, что при расширении спектра энергия сигнала превосходит энергию помех в N/D раз. Данное отношение N/D называют коэффициентом расширения спектра (processing gain) Gp.

Если считать размерность сигнала с шириной полосы W и длительностью Т приблизительно равной 2WТ, коэффициент расширения спектра можно записать в следующем виде.

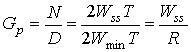(12.27)

где Wss — ширина полосы расширенного спектра (полная ширина полосы, используемая в методе расширения), Wmin, — минимальная ширина полосы данных (считается равной скорости передачи данных, R). Для систем с использованием метода прямой последовательности Wss и Wmin, приблизительно равны, соответственно, скорости передачи элементарных сигналов Rch и скорости передачи данных R. В результате можно записать следующее.

(12.28)

В данном случае под элементарным сигналом (chip) подразумевается наименьший непрерывный сигнал в системе. Для систем расширения спектра методом прямой последовательности элементарный сигнал представляет собой импульс (или элемент сигнала) псевдослучайного кода.

В любом случае использования расширенного спектра (например, для подавления интерференции или достижения высокого временного разрешения) коэффициент расширения спектра — это параметр, описывающий преимущество системы расширенного спектра перед узкополосной системой. В общем случае для модуляции сигнала в системе расширения спектра методом прямой последовательности используется схема BPSK или QPSK. Предположим, что двоичный символ состоит из 1000 элементарных кодовых сигналов BPSK. В соответствии с уравнением (12.28) коэффициент расширения спектра в данном случае будет равен 1000. Для демонстрации того, что такая система расширенного спектра позволяет более устойчивую передачу (относительно узкополосной системы), рассмотрим следующий пример. Представим, что в процессе обнаружения решение относительно значения принятого символа принимается для каждого из 1000 элементарных сигналов. Разумеется, в действительности такое не происходит; 1000 элементарных сигналов собираются, и проверяется их корреляция с кодом, что порождает единое решение относительно значения бита. Но даже если принять такую схему, то бит будет обнаружен правильно, даже если 499 решений из 1000 будут неверными.