Система связи служит для передачи сообщений от отправителя к получателю. Однако не всякое сообщение содержит информацию. Информация - это совокупность сведений об объекте или явлении, которые увеличивают знания потребителя об этом объекте или явлении.

В математической теории связи (теории информации) исходят из того, что в некотором сообщении xi количество информации I(xi) зависит не от её конкретного содержания, степени важности и т.д., а от того, каким образом выбирается данное сообщение из общей совокупности возможных сообщений.

В реальных условиях выбор конкретного сообщения производится с некоторой априорной вероятностью p(xi). Чем меньше эта вероятность, тем больше информации содержится в данном сообщении.

При определении количества информации исходят из следующих требований:

1. Количественная мера информации должна обладать свойством аддитивности: количество информации в нескольких независимых сообщениях должно равняться сумме количества информации в каждом сообщении.

2. Количество информации о достоверном событии (p(xi)=1) должно равняться нулю, так как такое сообщение не увеличивает наших знаний о данном объекте или явлении.

Указанным требованиям удовлетворяет логарифмическая мера, определяемая формулой

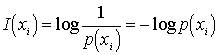. (1)

Чаще всего логарифм берется с основанием 2, реже - с основанием e:

двоичных единиц информации (бит),

натуральных единиц информации (нит).

Одну двоичную единицу информации содержит сообщение, вероятность выбора которого равняется 1/2. В этом случае

дв. ед. инф. (бит).

При применении натуральных логарифмов одну натуральную единицу информации содержит сообщение, вероятность выбора которого равняется 1/e:

нат. ед. инф. (нит).

Учитывая, что в практике передачи и преобразования информации широко применяются двоичные символы, двоичная логика, двоичные источники сообщений и двоичные каналы передачи, наиболее часто используется двоичная единица информации(бит).

Хотя при определении количества информации под сообщениями можно понимать любые фразы или телеграфные сообщения, мы здесь элементарными сообщениями будем называть отдельные буквы или слова. При использовании двухуровневых дискретных сигналов, например, мы будем пользоваться элементарными двоичными сигналами “1” и “0”, называя их буквами. Таким образом, алфавит двоичного источника состоит всего из двух букв, из которых можно строить более длинные комбинации, называемые кодовыми словами.

Вопросы

1. Что такое информация? Как определяется количество информации в сообщении?
2. Почему для определении количества информации в сообщении используется логарифмическая мера?
3. Какое сообщение содержит одну двоичную единицу информации?
4. Какое сообщение содержит одну натуральную единицу информации?