Для дискретных каналов с помехами Шеннон доказал теорему, имеющую фундаментальное значение в теории передачи информации. Эта теорема может быть сформулирована следующим образом.

Если производительность источника, где ε — сколь угодно малая величина, то существует способ кодирования, позволяющий передавать все сообщения источника со сколь угодно малой вероятностью ошибки. При такая передача невозможна.

Предположим, на вход канала поступают сигналы и, которые вызывают, на его выходе сигналы v. Предварительно будем полагать, что по каналу могут передаваться исключительно типичные последовательности (§6.3), состоящие из п сигналов и:. Соответственно на выходе канала сигналы при достаточно большом п образуют типичные последовательности: , содержащие типичные последовательности ошибок. Общее число типичных последовательностей и на основании (6.23) равно:

где Н(и) — энтропия сигналов и. Соответственно число типичных последовательностей V определяется как

(6.60)

где H(v) — энтропия сигналов v.

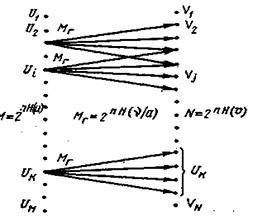
Рис. 6.3. Схема переходов типичных последовательностей сигналов от входа к выходу канала с шумами

Действие помех проявляется в том, что нарушается однозначное соответствие между последовательностями U и V, т. е. при передаче некоторой последовательности Ui возможно появление на выходе канала одной из нескольких последовательностей V. Процесс передачи в этих условиях можно представить так, как показано на рис. 6.3, где стрелками отмечены переходы от типичных последовательностей V к типичным последовательностям V. Так как последовательности ошибок типичные, то и переходы от U к V также являются типичными. Каждой последовательности U соответствует определенная группа типичных переходов, которая характеризует неопределенность, возникающую при передаче U. Количественно указанная неопределенность описывается произведением nH(v/u), где H(v/u) — условная энтропия сигналов при передаче сообщений и (6.48). Тогда в соответствии с (6.23) количество типичных переходов в каждой группе

(6.61)

В общем случае переходы перекрещиваются, т. е. одна и та же последовательность может образоваться в результате передачи одной из нескольких последовательностей U. Для того чтобы иметь возможность с высокой точностью однозначно определить принадлежность принятой последовательности V переданной последовательности U (на рис. 6.3 этому условию удовлетворяет. U), очевидно, необходимо между грушами последовательностейV установить достаточный интервал. Поэтому из всего набора последовательностей U только часть может использоваться для передачи информации.

Обозначим последовательности, выбранные для переноса информации, через UИ, а их число — буквой МИ. Выясним взаимосвязь МИс вероятностью ошибки при определении принадлежности V, т. е. взаимосвязь с вероятностью ошибки при декодирования принятых сигналов. Вероятности всех типичных переходов от U, к V одинаковы, поэтому полная вероятность ошибки равна вероятности перекрещивания переходов Р. Для вычисления Р. необходимо знать ансамбль последовательностей UИ. Иными словами, нужно указать конкретный способ кодирования. Решение вопроса об оптимальном выборе последовательностей UИ в общем случае представляет собой чрезвычайно сложную задачу, требующую отдельного рассмотрения. С целью ее упрощения будем полагать, что последовательности UИ выбираются из последовательностей U случайным образом. При этом условии вероятность того, что случайный переход от UИ к V будет перекрещиваться с другими переходами, приближенно равна отношению общего числа переходов ко всему количеству типичных последовательностей V. Следовательно, вероятность ошибки декодирования

(6.62)

Эта оценка вероятности ошибки является грубым приближением, однако она правильно указывает на характер зависимости Род от М и.

При согласовании канала с источником каждой типичной последовательности источника присваивается одна из последовательностей , поэтому их число МИвыбирается равным количеству типичных последовательностей источника. Если энтропия источника равна , то на основании (6.23) можно записать

(6.63)

Подставляя в (6.62) значения МИ, МГи N из (6.63), (6,61) и (6.60) и логарифмируя, получаем

Разделив это равенство на среднюю длительность сообщений в соответствии с (6.50), будем иметь

где

При максимальной скорости передачи сообщений по каналу и

(6.64)

Из выражения (6.62) следует, что вероятность ошибки декодирования Род может быть сколь угодно малой при неограниченном уменьшении g. Для того чтобы при этих, условиях сохранить достаточно малой величину ε, необходимо увеличивать количество сообщений п в типичных последовательностях. Что касается всех остальных нетипичных последовательностей из п сообщений, которые до сих пор не рассматривались, то их можно закодировать весьма сложными сигналами, обладающими высокой помехоустойчивостью, не заботясь о длительности таких сигналов, поскольку суммарная вероятность нетипичных последовательностей весьма кала и они не вызовут существенного уменьшения скорости передачи информации.

Таким образом, возможность одновременного установления сколь угодно малой вероятности ошибки декодирования Род и малой величины ε доказывает справедливость теоремы Шеннона.

Обратное утверждение теоремы о том, что при RИ>C декодирование со сколь угодно малой ошибкой невозможно, следует из того факта, что в этих условиях MИMГ>N и, следовательно, всегда будут иметь место перекрещивания переходов от U к V, coздающие неопределенность в установлении принадлежности V.

На первый взгляд может показаться, что поскольку вероятность ошибки в канале Р0монотонно уменьшается с увеличением длительности сигналов, то сколь угодно высокая достоверность при декодировании достигается только при неограниченном уменьшении скорости передачи. Теорема Шеннона доказывает, что наличие помех и ошибок в канале само по себе не препятствует передаче сообщений со сколь угодно малой вероятностью ошибок декодирования Род, а лишь ограничивает максимальную скорость передачи информации С. Высокая достоверность декодирования и конечная скорость передачи не исключают друг друга. В этом состоит чрезвычайно важное значение теоремы для теории и техники связи. Вместе с тем следует подчеркнуть, что из теоремы не вытекает конкретный способ наилучшего кодирования.

Применение на практике рассмотренного в теореме Шеннона общего метода, основанного на укрупнении кодируемых последовательностей, сильно усложняет кодирующие и декодирующие устройства и увеличивает задержку сигналов. Поэтому с инженерной точки зрения такой метод не эффективен. Однако теорема не утверждает, что укрупнение кодируемых сообщений является единственным способом. Поэтому в настоящее время продолжаются интенсивные поиски способов кодирования, которые бы позволяли с аппаратурой приемлемой сложности достигать предельных возможностей, указанных теоремой Шеннона.

Для обеспечения высокой достоверности передачи сообщений необходимо применять коды с избыточностью. Если R=C, то в соответствии с (6.50) средняя взаимная информация . В канале без помех она приобретает максимальное значение . Тогда коэффициент избыточности по аналогии с (6.12) равен:

(6.65)

Иными, словами, теорема утверждает, что для перелагай сообщений со сколь угодно малой вероятностью ошибки декодирования: Род могут быть найдены коды с минимальной избыточностью, равной χ. При передаче бинарных сигналов на основании (6.65), (6.33) и (6.58) минимальная избыточность равна:

(6.66)