6.3.1.1. Дискретный канал без памяти
6.3.2. Степень кодирования и избыточность
6.3.3. Коды с контролем четности
6.3.4. Зачем используется кодирование с коррекцией ошибок
6.3.4.1. Компромисс 1: достоверность илиполоса пропускания
6.3.4.2. Компромисс 2: мощность или полоса пропускания
6.3.4.3. Эффективность кодирования
6.3.4.4. Компромисс 3: скорость передачи данных или полоса пропускания
6.3.4.5. Компромисс 4: пропускная способность или ширина полосы пропускания
В разделе 4.8 мы рассмотрели цифровую передачу данных посредством M=2k сигналов (М-арная передача сигнала), где каждый сигнал содержит k бит информации. Было показано, что при ортогональной M-арной передаче сигналов уменьшения вероятности ошибки РB можно добиться путем увеличения М (расширения полосы пропускания). В разделе 6.1 мы показали, что РB можно уменьшить за счет кодирования k двоичных битов в одно из М ортогональных кодовых слов. Одним из основных недостатков ортогонального кодирования является неэффективное использование полосы пропускания. При наборе ортогональных кодов, включающем М=2k сигналов, требуемая ширина полосы пропускания в M/k раз больше необходимой для передачи некодированного сигнала. В этом и последующих разделах мы отойдем от рассмотрения ортогональных или антиподных свойств сигналов и сосредоточим внимание на классе процедур кодирования, известных как коды с контролем четности (parity-check codes). Эти процедуры канального кодирования относятся к структурированным последовательностям, поскольку они представляют методы введения в Исходные данные структурированной избыточности таким образом, что это позволяет обнаруживать или исправлять ошибки. Как показано на рис. 6.1, структурированные последовательности делятся на три подкатегории: блочные, сверточные и турбокоды. Блочное кодирование рассматривается в этой главе, а другие описываются в главах 7 и 8.
6.3.1. Модели каналов
6.3.1.1. Дискретный канал без памяти
Дискретный канал без памяти (discrete memoryless channel — DMC) характеризуется дискретным входным алфавитом, дискретным выходным алфавитом и набором условных вероятностей 
где i представляет модулятор M-арного входного символа, j — демодулятор Q-арного выходного символа, a P(i\j) — это вероятность приема символа j при переданном символе i. Каждый выходной символ канала зависит только от соответствующего входного символа, так что для данной входной последовательности 
условную вероятность соответствующей выходной последовательности Z = z1,z2,...,zm,..., zn можно записать следующим образом.
(6.12)
Если же канал имеет память (т.е. в пакете данных имеются помехи или канал подвергается воздействию замирания), условную вероятность последовательности Z нужно выражать как совместную вероятность всех элементов последовательности. Уравнение (6.12) — это условие отсутствия памяти у канала. Поскольку считается, что шум в канале без памяти влияет на каждый символ независимо от других, то в этом случае условная вероятность Z является произведением вероятностей независимых элементов.
6.3.1.2. Двоичный симметричный канал
Двоичный симметричный канал (binary symmetric channel — BSC) является частным случаем дискретного канала без памяти, входной и выходной алфавиты которого состоят из двоичных элементов (0 и 1). Условные вероятности имеют симметричный вид.
и (6.13)
Уравнение (6.13) выражает так называемые вероятности перехода. Иными словами, при передаче канального символа вероятность принятия его с ошибкой равна р (относительно значения энергии), а вероятность того, что он передан без ошибки, — (1-р). Поскольку на выход демодулятора поступают дискретные элементы 0 или 1, говорят, что по отношению к каждому символу демодулятор принимает жесткое решение (hard decision). Рассмотрим наиболее распространенную схему кодирования — данные в формате BPSK плюс демодуляция по принципу жесткого решения. Вероятность появления ошибки в канальном символе находится с использованием метода, обсуждавшегося в разделе 4.7.1, и дается уравнением (4.79).
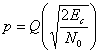
Здесь EJN0 — отношение энергии канального символа к плотности помех, а функция Q(x) была определена в уравнении (3.43).
Если описанная схема жестких решений применяется в системах с бинарными кодировками, то с демодулятора на декодер поступают двоичные кодовые символы или биты канала. Поскольку декодер работает на основе жестких решений, определяемых демодулятором, декодирование в двоичном симметричном канале называется также жестким декодированием.
6.3.1.3. Гауссов канал
Определение двоичного симметричного канала можно использовать и для каналов с недискретным алфавитом. Пример — гауссов канал с дискретным входным алфавитом и непрерывным выходным алфавитом, лежащим в диапазоне (
). Этот канал добавляет шум ко всем передаваемым символам. Поскольку шум — это гауссова случайная переменная с нулевым средним и дисперсией σ2, результирующую функцию плотности вероятности принятой случайной величины z при условии передачи символа uk (правдоподобие uk) можно записать следующим образом.
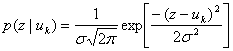(6.14)
для всех z, где k = 1,2,..., М.
В этом случае отсутствие памяти имеет то же значение, что и в разделе 6.3.1.1, а само уравнение (6.12) можно использовать при вычислении условной вероятности для последовательности Z.
Если на выходе демодулятора находится непрерывный алфавит или его квантовое приближение (с более чем двумя квантовыми уровнями), говорят, что демодулятор принимает мягкое решение (soft decision). Если в системе используется кодирование, демодулятор подает такие квантовые кодовые символы на декодер. Поскольку декодер работает на основе мягких решений, определяемых демодулятором, декодирование в гауссовом канале называется мягким.
В канале с жестким решением процесс обнаружения можно описать через вероятность символьной ошибки. Но в канале с мягкими решениями выбор детектора нельзя однозначно отнести к верному или неверному. Таким образом, поскольку определенного решения не существует, не может быть и выражения для вероятности ошибки; детектор может только определять семейство условных вероятностей или правдоподобий разных типов символов.
В принципе, декодеры с мягкими решениями можно сделать, но для блочных кодов они будут значительно сложнее декодеров с жесткими решениями; поэтому, как правило, блочные коды реализуются в системах с декодерами, работающими по принципу жесткого решения. Для свёрточных кодов реализация и жестких, и мягких решений одинаково популярна. В этой главе мы предполагаем, что каналы являются двоичными симметричными и, следовательно, декодеры используют жесткие решения. В главе 7 мы перейдем к обсуждению жесткого и мягкого декодирования для свёрточных кодов, а также продолжим обсуждение моделей канала.
6.3.2. Степень кодирования и избыточность
При использовании блочных кодов исходные данные делятся на блоки из k бит, которые иногда называют информационными битами, или битами сообщения; каждый блок может представлять любое из 2k отдельных сообщений. В процессе кодирования каждый k-битовый блок данных преобразуется в больший блок из п бит, который называется кодовым битом, или канальным символом. К каждому блоку данных кодирующее устройство прибавляет (n - k) бит, которые называются избыточными битами (redundant bits), битами четности (parity bits), или контрольными битами (check bits); новой информации они не несут. Для обозначения описанного кода используется запись (n, k). Отношение числа избыточных бит к числу информационных бит, (n - k)/k, называется избыточностью (redundancy) кода; отношение числа бит данных к общему числу бит, k/n, именуется степенью кодирования (code rate). Под степенью кодирования подразумевается доля кода, которая приходится на полезную информацию. Например, в коде со степенью 1/2, каждый кодовый бит несет 1/2 бит информации.
В этой главе и в главах 7 и 8 мы рассмотрим методы кодирования, получающие избыточность за счет увеличения необходимой ширины полосы. Например, метод защиты от ошибок, использующий код со степенью 1/2 (100%-ная избыточность), будет требовать двойной, по сравнению с некодированной передачей, полосы пропускания. В то же время, если использовать код со степенью 3/4, то избыточность составит 33%, и увеличение полосы пропускания будет всего 4/3. В главе 9 мы рассмотрим методы модуляции/кодирования для узкополосных каналов, где защита от ошибок происходит не за счет увеличения полосы пропускания, а за счет усложнения метода (и, как следствие, его аппаратной реализации).
6.3.2.1. Терминология в кодировании
Разные авторы по-разному называют элементы на выходе кодирующего устройства: кодовые биты (code bits), канальные биты (channel bits), кодовые символы (code symbols), канальные символы (channel symbols), биты четности (parity bits), символы четности (parity symbols). Вообще, по смыслу эти термины очень похожи между собой. В этой книге для двоичных кодов .термины "кодовые биты", "канальные биты", "кодовые символы" и "канальные символы" употребляются как синонимы. Следует уточнить, что названия "кодовые биты" и "канальные биты" подходят для описания только двоичных кодов. Такие общие названия, как "кодовые символы" и "канальные символы", зачастую более предпочтительны, поскольку они могут означать как двоичное, так и любое другое кодирование. Отметим, что эти понятия не следует путать с тем, что получается при группировке битов в передаваемые символы, о которых шла речь в предыдущей главе. Термины "биты четности" k "символы четности" применяются только к тем составляющим кода; которые представляют избыточные компоненты, прибавляемые к исходным данным.
6.3.3. Коды с контролем четности
6.3.3.1. Код с одним контрольным битом
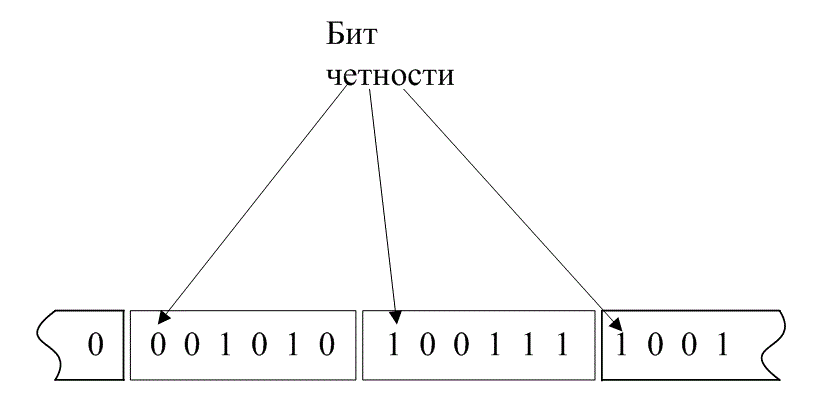
Коды с контролем четности (parity-check code) для обнаружения или исправления ошибок используют линейные суммы информационных битов, которые называются символами (parity symbols), или битами четности (parity bits). Код с одним контрольным битом — это прибавление к блоку информационных битов одного контрольного бита. Этот бит (бит четности) может быть равен нулю или единице, причем его значение выбирается так, чтобы сумма всех битов в кодовом слове была четной или нечетной. В операции суммирования используется арифметика по модулю 2 (операция исключающего ИЛИ), описанная в разделе 2.9.3. Если бит четности выбран так, что результат четный, то говорят, что схема имеет положительную четность (even parity); если при добавлении бита четности результирующий блок данных является нечетным, то говорят, что он имеет отрицательную четность (odd parity). На рис. 6.8, а показана последовательная передача данных (первым является крайний справа бит). К каждому блоку добавляется один бит четности (крайний слева бит в каждом блоке), дающий положительную Четность.
а)
б)
Рис. 6.8. Проверка четности для последовательной и параллельной структуры кода: а) последовательная структура; б) параллельная структура
В приемном оконечном устройстве производится декодирование, заключающееся в проверке, дают ли нуль суммы принятых битов кодового слова по модулю 2 (положительная четность). Если полученный результат равен 1, то кодовое слово заведомо содержит ошибки. Степень кодирования такого кода можно записать как k/(k + 1). Как вы думаете, может ли декодер автоматически исправить цифру, полученную с ошибкой? Нет, это невозможно. Можно только обнаружить, что в кодовом символе присутствует нечетное количество ошибок. (Если ошибка была внесена в четное число битов, то проверка четности покажет отсутствие ошибок; данный случай — это пример необнаруженной ошибки.) Предполагая, что ошибки во всех разрядах равновероятны и появляются независимо, можно записать вероятность появления у ошибок в блоке, состоящем из я символов.
(6.15)
Здесь р — вероятность получения канального символа с ошибкой, а через
(6.16)
— обозначается число различных способов выбора из и бит j ошибочных. Таким образом, для кода с одним битом четности вероятность необнаруженной ошибки Рnd в блоке из п бит вычисляется следующим образом.
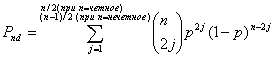(6.17)
Пример 6.1. Код положительной четности
Нужно создать код обнаружения ошибок (4, 3) положительной четности, причем символ четности должен располагаться на крайней левой позиции кодового слова. Какие ошибки может обнаружить код? Вычислите вероятность необнаруженной ошибки сообщения, предполагая, что все символьные ошибки являются независимыми событиями и вероятность ошибки в канальном символе равна р = 10-3.
Решение
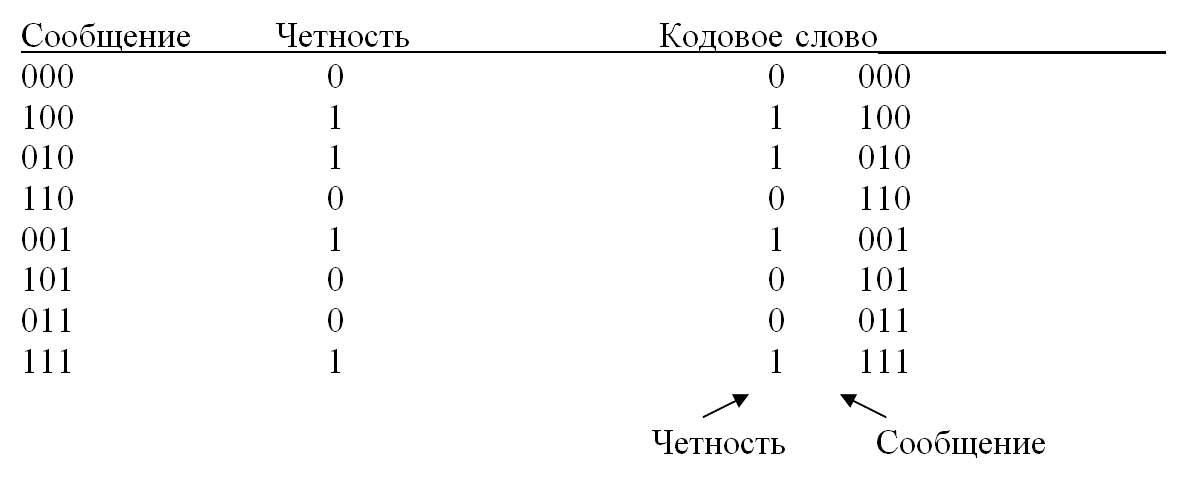
Код может выявлять все комбинации с одной или тремя ошибками. Вероятность необнаруженной ошибки равна вероятности появления где-либо в кодовом слове двух или четырех ошибок.
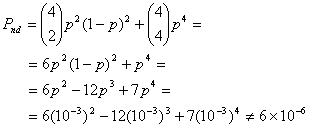
6.3.3.2. Прямоугольный код
Прямоугольный код (rectangular code), называемый также композиционным (product code), можно представить в виде параллельной структуры кода, изображенной на рис. 6.8, б. Код создается следующим образом. Вначале из битов сообщения строятся прямоугольники, состоящие из М строк и N столбцов; затем к каждой строке и каждому столбцу прибавляется бит четности, что в результате дает матрицу размером (М+ 1) х (N+1). Степень кодирования прямоугольного кода, k/n, может быть записана следующим образом.
Насколько прямоугольный код мощнее кода, который имеет один контрольный бит и предоставляет только возможность обнаружить ошибку? Отметим, что любая отдельная ошибка в разряде приведет к нарушению четности в одном столбце и в одной из строк матрицы. Следовательно, прямоугольный код может исправить любую единичную ошибку, поскольку расположение такой ошибки однозначно определяется пересечением строки и столбца, в которых была нарушена четность. В примере, показанном на рис. 6.8, б, размеры матрицы равны М= N = 5; следовательно, на рисунке отображен код (36, 25), способный исправлять единичные ошибки, расположенные, в любом из 36 двоичных разрядов. Вычислим для такого блочного кода с коррекцией ошибок вероятность появления неисправленной ошибки, для чего учтем все способы появления ошибки сообщения. Исходя из вероятности наличия j ошибок в блоке из п символов, записанной в выражении (6.5), можно записать вероятность ошибки сообщения, называемой также блочной ошибкой или ошибочным словом, для кода, который может исправить ошибочные комбинации, состоящие из t или менее ошибочных битов.
(6-18)
Здесь р — вероятность получения ошибочного канального символа. В примере на рис. 6.8, б код может исправить все однобитовые ошибки (t = 1) в прямоугольном блоке, состоящем из n = 36 бит. Следовательно, суммирование в уравнении (6.18) начинается с j = 2.
При достаточно малом р, наибольший вклад дает первое слагаемое суммы. Следовательно, для примера с прямоугольным кодом (36, 25) можно записать следующее.
Точная вероятность битовой ошибки РВзависит от конкретного кода и используемого декодера. Приближенные значения РB приводятся в разделе 6.5.3.
6.3.4. Зачем используется кодирование с коррекцией ошибок?
Кодирование с коррекцией ошибок можно рассматривать как инструмент, реализующий различные компромиссы системы. На рис. 6.9 приведен сравнительный вид двух кривых, описывающих зависимость достоверности передачи от отношения Eb/N0 Одна кривая соответствует обычной схеме модуляции без кодирования, а вторая представляет такую же модуляцию, но уже с использованием кодирования; Ниже подробно рассмотрено четыре компромисса, имеющие место при канальном кодировании.
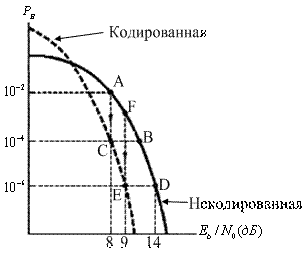
Рис. 6.9. Сравнение типичной достоверности передачи при использовании схемы с кодированием и схемы без кодирования
6.3.4.1. Компромисс 1: достоверность или полоса пропускания
Представим себе, что разработана простая, недорогая система речевой связи, которая была установлена у заказчика. Система не использует кодирование с коррекцией ошибок. Пусть рабочая точка системы совпадает с точкой А на рис. 6.9 (Eb/N0 = 8 дБ, РВ - 10-2). После нескольких испытаний у заказчика появляются жалобы на качество связи; Он полагает, что вероятность появления битовой ошибки должна быть не выше 10-4. Обычным способом удовлетворения требования заказчика является сдвиг рабочей точки из точки А, например, в точку В (рис. 6.9). В то же время допустим, что Eb/N0, равное 8 дБ, — это максимальное значение, возможное в данной системе. Из рис. 6.9 видим, что один из возможных выходов из ситуации (компромиссов) — это сдвиг рабочей точки из точки А в точку С. Иными словами, "съехав" по вертикали вниз в точку С на кривой, отвечающей кодированному случаю, можно предоставить заказчику более высокую достоверность передачи данных. Чего это будет стоить? Помимо введения новых компонентов (кодера и декодера), это приведет к увеличению необходимой полосы пропускания. Кодирование с коррекцией ошибок требует избыточности. Если предположить, что связь будет происходить в реальном времени (так что сообщения не могут задерживаться), добавление избыточных битов потребует увеличения, скорости передачи и, конечно же, большей полосы пропускания.
6.3.4.2. Компромисс 2: мощность или полоса пропускания
Допустим, заказчику установлена система без кодирования £ рабочей точкой, совпадающей с точкой D на рис. 6.9 (Eb/N0 = 14 дБ, РB = 10-6). Заказчик не имеет претензий к качеству связи, но с помощью данного оборудования затруднительно получить требуемые Eb/N0 = 14 дБ. Иными словами, оборудование постоянно работает на грани отказа. Если снизить требования к Eb/N0 или мощности, то проблем с надежностью оборудования можно избежать. В контексте рис. 6.9 данные меры выглядят как сдвиг рабочей т,очки из D в E. Другими, словами, требуемое значение Eb/N0 можно получить, если применить кодирование с коррекцией ошибок. Таким образом, при фиксированном качестве связи компромисс заключается в получении большей производительности при снижении требований к мощности или Eb/N0. Чем за это приходится платить? Тем же, чем и в прошлый раз, — большей полосой пропускания.
Заметим, что в системах, где не используется связь в реальном времени, применение кодирования с коррекцией ошибок даст несколько отличные результаты. Повышение достоверности передачи или понижение потребляемой мощности (подобное описанным выше случаям 1 или 2) будет достигаться за счет увеличения времени задержки, а не за счет расширения полосы пропускания.
6.3.4.3. Эффективность кодирования
Пример компромиссных решений, рассмотренный в предыдущем разделе, позволяет понизить Eb/N0 с 14 до 9 дБ при поддержании той же достоверности передачи. В контексте этого примера и с помощью рис. 6.9 мы можем ввести понятие эффективность кодирования (coding gain). Итак, при данной вероятности битовой ошибки эффективность кодирования определяется как уменьшение Eb/N0, которое достигается при использовании кодирования. Эффективность кодирования G, как правило, выражается в децибелах.
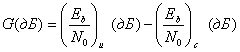(6.19)
Здесь (Eb/N0)u и (Eb/N0)с— требуемые некодированное и кодированное значения.
6.3.4.4. Компромисс 3: скорость передачи данных или полоса пропускания
Пусть разработана система без кодирования с рабочей точкой, совпадающей с точкой D на рис. 6.9 (Eb/N0 = 14 дБ, РB =10-6). Допустим, что с качеством данных нет никаких проблем и нет особой нужды в снижении мощности. Однако у заказчика возросли требования к скорости передачи данных. Напомним в связи с этим уравнение (5.20,6).
Если в системе ничего не менять, кроме скорости передачи данных R, то из приведенного выше выражения видно, что это приведет к уменьшению значения Eb/N0 и перемещению рабочей точки вверх, например из точки D в некоторую точку F. А теперь представим, что она "съезжает" вниз по вертикали в точку Е на кривую, которая представляет кодированную модуляцию. Возрастание скорости передачи данных плохо отражается на качестве их передачи. В то же время применение кодирования с коррекцией ошибок восстанавливает утраченное качество, сохраняя при этом прежний уровень мощности (Pr/N0). Итак, значение Eb/N0 понижено, но код способствует получению той же вероятности ошибки при сниженном значении Eb/N0. Какова цена такого увеличения скорости передачи данных или увеличения емкости? Как и раньше, это увеличение полосы пропускания.
6.3.4.5. Компромисс 4: пропускная способность или ширина полосы пропускания
Компромисс 4 сходен с компромиссом 3 в том, что оба дают возрастание пропускной способности. Метод множественного доступа, именуемый множественным доступом с кодовым разделением каналов (code-division multiple access — CDMA), который описывается в главе 12, — это один из стандартов, используемых в сотовой связи. При CDMA, когда все клиенты совместно используют общий спектр частот, каждый клиент является источником помех для других пользователей в той же ячейке или соседних. Поэтому пропускная способность (максимальное число клиентов) ячейки обратно пропорциональна значению Eb/N0 (см. раздел 12.8). При этом снижение Eb/N0 дает в итоге увеличение пропускной способности; код позволяет снизить мощности, используемые каждым клиентом, что, в свою очередь, приводит к увеличению общего числа клиентов. И снова платой за это является увеличение полосы пропускания. Но в этом случае увеличение полосы сигнала, получаемое при переходе к кодированию с коррекцией ошибок, незначительно, по сравнению с существенным увеличением полосы пропускания, получаемым при расширении спектра сигнала; поэтому при передаче данных оно не оказывает влияния на полосу пропускания.
В каждом из упомянутых выше компромиссов предполагалось использование "традиционного" кода с избыточными битами и более быстрая передача сигналов (для систем связи реального времени); следовательно, в каждом случае платой было расширение полосы передачи. В то же время существуют методы коррекции ошибок, называемые решетчатым кодированием (trellis-coded modulation), которые не требуют увеличения скорости передачи сигналов или расширения полосы частот для систем связи реального времени. (Эти методы рассмотрены в разделе 9.10.)
Пример 6.2. Связь вероятности ошибки с использованием кодирования
Сравните вероятность ошибки в сообщении для двух каналов связи — обычного и использующего кодирование с коррекцией ошибок. Пусть некодированная передача имеет следующие характеристики: модуляция BPSK, гауссов шум, Pr/N0 = 43 776, скорость передачи данных R — 4800 бит/с. Для случая с кодированием предполагается использование кода с коррекцией ошибок (15, 11), предоставляющего возможность исправления любых однобитовых ошибочных комбинаций кода в блоке из 15 бит. Будем считать, что демодулятор принимает жесткие решения и передает демодулированный код прямо на декодер, который, в свою очередь, определяет исходное сообщение.
Решение
Используем уравнение (4.79). Пусть 
и 
—вероятности символьных ошибок в канале без кодирования и в канале с кодированием, где 
— отношение энергии бита к спектральной плотности мощности шума, a — отношение энергии кодированного бита к спектральной плотности мощности шума.
Без кодирования
и
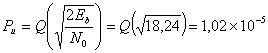(6.20)
Для Q(x) используется следующее приближение, приведенное в уравнении (3.44).
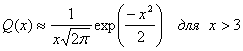
Вероятность того, что некодированный блок сообщений 
будет принят с ошибкой, равна 1 минус произведение вероятностей того, что каждый бит будет обнаружен правильно. Таким образом,
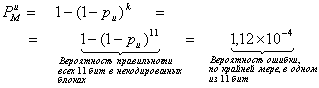(6.21)
С кодированием
Допустим, рассматриваемая система — это система связи реального времени, где задержки недопустимы, а скорость передачи канальных символов, или скорость передачи кодированных битов, равна Rc = 15/11 скорости некодированной передачи.
и
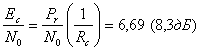
Для каждого кодового бита значение меньше, чем в случае с некодированными битами данных. Это объясняется тем, что скорость передачи канальных битов возросла, а мощность передатчика при этом не изменилась.
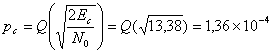(6.22)
Сравнивая выражения (6.20) и (6.22), можно видеть, что вследствие внесения избыточности вероятность ошибки в канальном бите уменьшилась. За то же время и с теми же номинальными мощностями нужно обнаружить большее число бит; повышение производительности в результате кодирования еще не очевидно. Вычислим теперь с помощью уравнения (6.18) частоту появления ошибок в кодированном сообщении Рсм.
Суммирование начинается с j = 2, поскольку код позволяет исправлять все однобитовые ошибки в блоках из n = 15 бит. Достаточно хорошее приближение можно получить, используя только первый член суммы. Для рс используем значение, полученное из уравнения (6.22).
(6.23)
Сравнивая выражения (6.21) и (6.23), можно видеть, что вследствие применения кода с коррекцией ошибок вероятность ошибки сообщения была уменьшена примерно в 58 раз. Данный пример иллюстрирует типичное поведение систем связи реального времени при использовании кодирования с коррекцией ошибок. Введение избыточности означает увеличение скорости передачи сигналов, уменьшение энергии, приходящейся на канальный символ, и увеличение числа ошибок вне демодулятора. Преимуществом такого подхода является то, что декодер (при разумном значении ) позволяет с лихвой компенсировать слабую производительность демодулятора.
6.3.4.6. Характеристики кода при низком значении
В конце данной главы читателю предлагается решить задачу 6.5, сходную с примером 6.2. В п. а задачи 6.5, где значение принимается равным 14 дБ, кодирование дает повышение достоверности передачи сообщения. В то же время в п. б, где значение снижается до 10 дБ, кодирование не дает улучшения; фактически происходит ухудшение. Может возникнуть вопрос, почему в п. б происходит такое ухудшение? По сути, в обоих пунктах задачи применяется одна и та же процедура. Ответ можно найти на рис. 6.9, который наглядно показывает связь между кодированными и некодированными вероятностями ошибки. Хотя в задаче 6.5 речь идет о вероятности ошибки сообщения, а на рис. 6.9 приведен график битовой ошибки, следующее объяснение остается в силе. Итак, на подобных графиках кривые пересекаются (как правило, при низких значениях ). Смысл этого пересечения (порога) в том, что у всех систем кодирования имеется ограниченная способность к коррекции ошибок. Если в блоке имеется больше ошибок, чем способен исправить код, система будет работать плохо. Представим себе, что значение снижается непрерывно. Что мы увидим на выходе демодулятора? Демодулятор будет допускать все больше и больше ошибок. Следовательно, такое постепенное уменьшение должно в конце концов создать пороговую ситуацию, когда декодер будет переполнен ошибками. При достижений этого порога снижение производительности можно объяснить поглощением энергии избыточными битами, которые не дают никакого выигрыша. Не удивляет ли читателя то, что в области (низких значений ), где больше всего следовало бы ожидать улучшения достоверности передачи, код имеет наименьшую эффективность? Впрочем, существует класс мощных кодов, называемых турбокодами (turbo code), которые позволяют повысить надежность передачи при низких значениях ; у турбо-кодов точка пересечения графиков находится значительно ниже, чем у сверточных кодов. (Турбокоды рассматриваются в разделе 8.4.)