Условием существования направляемой моды является экспоненциальное убывание её поля в оболочке вдоль координаты r, причём степень уменьшения напряжённости с ростом r определяется значением n, уменьшение которого приводит к перераспределению поля в оболочку ОВ – появлению вытекающих волн. При n=0 происходит качественное изменение волнового процесса, заключающегося в невозможности существования направляемой моды. Этот режим называется критическим, в связи с чем очень важно определение условий его возникновения, что можно осуществить подстановкой в последнее уравнение значения n=0, в результате чего правые части уравнений обращаются в бесконечность и для Е и Н мод будет справедливо условие [7]

I₀`(cr)=0, (3.3.1)

которое определяет границы их возникновения или исчезновения.

Последнее уравнение имеет бесчисленное множество решений, поэтому, обозначив положительный корень через p_0m, а также используя выражения для c и n, мы получим

.

Введём величину, которая носит название нормированной частоты

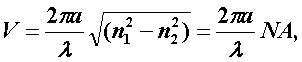(3.3.2)

где а – радиус сердцевины волокна.

Это один из важнейших обобщающих параметров, используемых для оценки свойств ОВ, который связывает его структурные параметры и длину световой волны, распространяемой в волокне.

С увеличением радиуса сердцевины волокна величина V растет, а с увеличением длины волны уменьшается. В табл. 3.1. приведены соотношения нормированной частоты, длины волны и радиуса сердцевины при различных значениях коэффициента преломления оболочки (n₁=1,51) [11].

Таблица 3.1 – Соотношения для нормированной частоты

Одномодовый режим реализуется, если нормированная частота V≤2,405.Чем меньше разность ∆n=n₁-n₂, тем при большем радиусе световода обеспечивается одномодовый режим.

В этом случае:

(3.3.3)

и при n=0 для каждого из корней имеет место критическое значение нормированной частоты:

P_0m = c_кр а = V_0m, где m = 1,2,3,…M, а

p₀₁ = 2,405; p₀₂ = 5,520; p₀₃ = 8,654 и т. д.

Если для некоторой симметричной моды нормированная частота больше её критического значения (V>V_0m), то она распространяется в ОВ, в противном случае – нет. Так, при 2,405<V<5,520 в ОВ распространяются моды Е₀₁ и Н₀₁, а при 5,520<V<8,654 к ним добавляются моды Е₀₂ и Н₀₂ и т.д., в то время как неравенство V<2,405 указывает на отсутствие симметричных мод.

Последняя формула позволяет определить значения критических длин волн l_0m^кр для симметричных волн в виде [2]

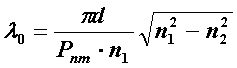, (3.3.4)

или, переходя к частоте,

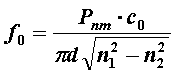. (3.3.5)

Очевидно, что для распространяющейся моды должно выполняться условие l<l_0m^кр, то есть V>V_0m, в противном случае этой моды нет.

В отличие от симметричных мод несимметричные имеют все шесть составляющих векторов электромагнитного поля и их невозможно разделить на электрические и магнитные. Критическая нормированная частота в этом случае определяется выражением [7]

V_nm = p_nm, n = 1, 2, 3 … N; m = 1, 2, 3, … M, (3.3.6)

где p_nm – положительный корень соответствующего трансцендентного уравнения, который характеризует тип волны (моду) и может быть определен из таблицы 3.2 [11]

Таблица 3.2 – Значения корней трансцендентного уравнения

Среди направляемых мод особое положение занимает мода НЕ₁₁, у которой критическое значение нормированной частоты n = 0. Это основная (фундаментальная) мода ступенчатого ОВ, так как она распространяется при любой частоте и структурных параметрах волокна. С точки зрения геометрической оптики, она образуется лучом, вводимым вдоль оси волокна, так как только характеристики такого луча не зависят от условий отражения на границе «сердцевина – оболочка». Выбирая параметры ОВ, можно получить режим распространения только этой моды, что реализуется при условии

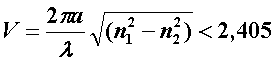. (3.3.7)