Да, существуют. В литературе типовыми звеньями дискретных цепей считаются звенья 1-го и 2-го порядков. Они получаются из общей структуры рис. 46, если оставить в ней только один либо два элемента задержки.
На рис. 53,а показано звено 1-го порядка с передаточной функцией
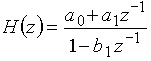
и АЧХ
.
Типовое звено 2-го порядка изображено на рис. 53,б. Его передаточная функция
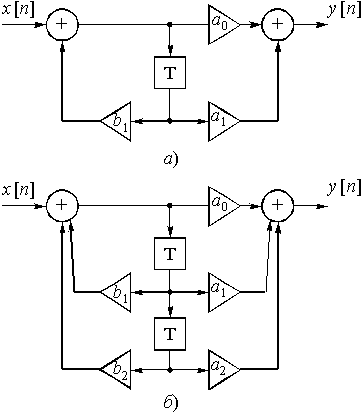
Рис. 53
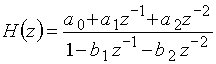
и АЧХ
.
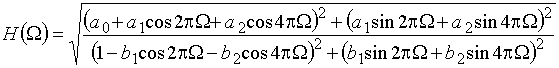Пример 18.1. Построим график АЧХ звена первого порядка, у которого 
, 
.
Передаточная функция такого звена первого порядка
.
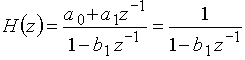Амплитудно-частотная характеристика
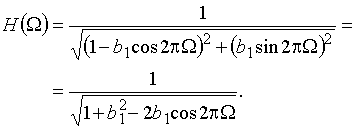
Поскольку полюс 
передаточной функции 
равен 
, то для того, чтобы цепь была устойчивой необходимо выбирать значения 
такими, чтобы выполнялось условие 
.
На рис. 54 приведены графики АЧХ, построенные для значений 
= 0,5 и 
= -0,5.
АЧХ рассматриваемого фильтра зависит от знака коэффициента 
. При 
> 0 получаем режекторный фильтр, при 
< 0 - полосовой.
Пример 18.2. Найдем передаточную функцию и построим график АЧХ звена 2-го порядка (рис. 52,б) при 
, 
, 
= 0,2 и 
= -0,4.
Передаточная функция такого звена
.
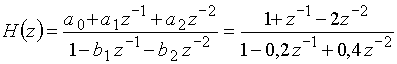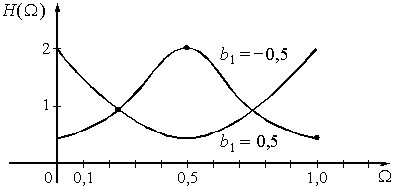
Рис. 54
Как указывалось ранее (Вопрос 15), рекурсивную цепь с прямыми и обратными связями можно представить как каскадное соединение рекурсивного фильтра с передаточной функцией 
и нерекурсивного фильтра с передаточной функцией 
. В нашем случае, для звена второго порядка,
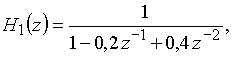
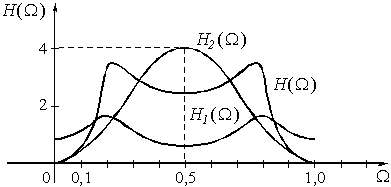
Рис. 55
График АЧХ для 
уже был построен и приведен на рис. 52. АЧХ 
рекурсивного фильтра рассчитывается по формуле
.
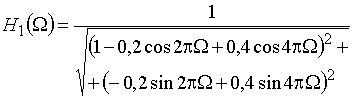Графики 
, 
и 
изображены на рис. 55.
Самоконтроль
1. Какова структура звеньев 1-го и 2-го порядков дискретных цепей?
2. Как рассчитываются передаточные функции типовых звеньев дискретных цепей?
3. Запишите выражения для выходных напряжений 
звеньев 1-го и 2-го порядков.