Частотный метод является достаточно эффективным и наглядным при анализе передачи сигналов через линейную систему. Он позволяет оценить частотные искажения в канале связи, требования к характеристикам электрической цепи. Особенно важно определить требования к АЧХ и ФЧХ цепи с точки зрения искажения формы сигнала. Определим условия неискажаемой передачи сигнала через линейную систему. Предположим, что на входе линейной цепи, как четырехполюсника действует сигнал f1(t) определенной формы (рис. 9.12). На выходе в результате прохождения сигнала через четырехполюсник с комплексной передаточной функцией H(jw) амплитуда сигнала может измениться (на рис. 9.12 уменьшилась), и сигнал вследствие конечности скорости его распространения может запаздывать относительно входного воздействия на t0. Однако важно, чтобы при этом не изменилась форма сигнала. Таким образом, условие безыскаженной передачи можно сформулировать с помощью равенства
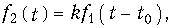
где k – некоторая вещественная постоянная; t0 –время задержки (запаздывания) выходного сигнала относительно входного. Применив к (9.52) прямое преобразование Фурье и учтя свойство линейности и теорему запаздывания, перепишем условие (9.52) в частотной области:
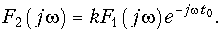
Так как комплексная передаточная функция цепи с учетом (4.5) должна быть
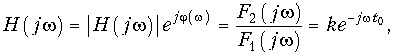
то отсюда получаем требование к АЧХ и ФЧХ неискажающей цепи
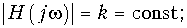
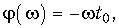
т. е. для того, чтобы линейная цепь не искажала форму сигнала ее АЧХ должна быть равномерной (рис. 9.13, а), а ФЧХ – линейной (рис. 9.13, б).
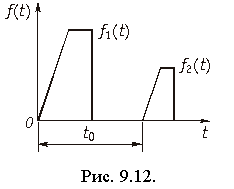
Условие безыскаженной передачи во всем частотном диапазоне можно выполнить лишь для резистивных цепей. В цепях с реактивными элементами условия (9.54) и (9.55) можно обеспечить лишь в ограниченном частотном диапазоне w0 (на рис. 9.13 показано пунктиром).
В этой связи представляет практический интерес вопрос о влиянии на форму сигнала отклонения АЧХ и ФЧХ от идеальной. Рассмотрим в качестве примера прохождение сигнала в форме единичной функции, в форме единичного импульса и импульса прямоугольной формы через цепь с АЧХ, изображенной на рис. 9.14. Эта цепь соответствует идеальному ФНЧ и задается условием
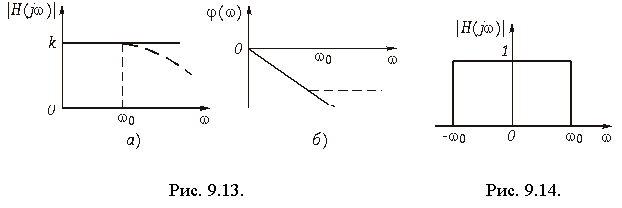
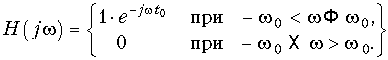
Фильтр нижних частот пропускает без искажений все частотные составляющие от 0 до w0 и задерживает составляющие больше w0.
Единичный импульс. Рассмотрим вначале входной сигнал f1(t) в форме единичного импульса (рис. 7.2, б). Так как для единичного импульса F1(jw) = 1, то с учетом (9.56) и обратного преобразования Фурье (9.7), получим:
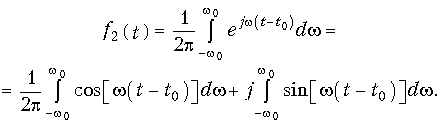
Учитывая, что второй интеграл равен нулю, окончательно после интегрирования получаем:
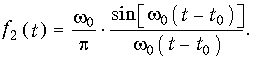
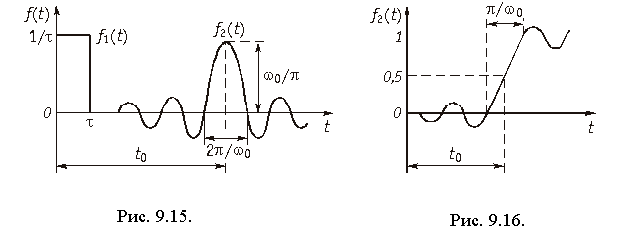
На рис. 9.15 изображена форма выходного сигнала f2(t), определяемая функцией (9.57). Из рисунка видно, что форма выходного сигнала существенно отличается от входного импульса f1(t): он искажается по форме и растягивается во времени (теоретически на бесконечность), что отражает установленное ранее соотношение между длительностью сигнала и шириной его спектра: сигнал ограниченный по частоте — бесконечен во времени и наоборот. Запаздывание выходного сигнала t0 определяется крутизной ФЧХ: t0 = —dj/dw). С увеличением w0 (с расширением полосы пропускания фильтра) ширина главного лепестка импульса равная 2p/w0 — сужается, задержка t0 уменьшается, амплитуда импульса увеличивается. Важно отметить, что теоретически согласно (9.57) сигнал f2(t) существует и при t < 0, т. е. до воздействия входного сигнала, что конечно, противоречит условию физической реализуемости и является следствием идеализации АЧХ ФНЧ.
Единичный сигнал. Рассмотрим теперь прохождение сигнала в форме единичной функции (рис. 7.2, а) через ФНЧ с характеристикой (9.56). Запишем уравнение единичной функции 1(t) в интегральной форме:
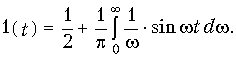
Интеграл в (9.58) можно рассматривать как вещественную форму обратного преобразования Фурье (9.7) для нечетной функции f(t) = 1(t) – 1/2, спектр которой равен 1/w. Тогда на основании (9.58) и с учетом условий (9.52) и (9.56), для выходного сигнала можно записать:
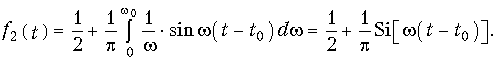
Интеграл в (9.59) табулирован и носит название интегрального синуса: Si[w(t – t0)]. На рис. 9.16 приведен график сигнала на выходе идеального ФНЧ, определяемой функцией (9.59).
Как следует из представленного графика, чем уже полоса пропускания ФНЧ (меньше w0), тем меньше крутизна фронта нарастания импульса:df2/dt = w0/p. Таким образом, как и в случае единичного импульса для уменьшения искажений выходного сигнала необходимо расширять полосу пропускания ФНЧ. Выбросы в выходном сигнале обусловлены теми же причинами, что и в случае, изображенном на рис. 9.15 (идеализация АЧХ ФНЧ).
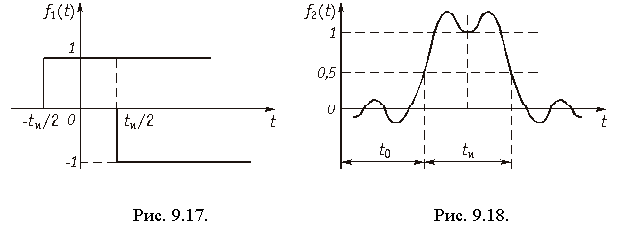
Прямоугольный импульс можно рассматривать как разность двух единичных функций сдвинутых относительно друг друга на tи/2 (рис. 9.17). Тогда учитывая линейность цепи и равенство (9.59) получим уравнение выходного сигнала для этого случая:
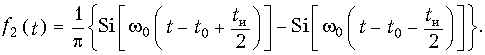
На рис. 9.18 изображен вид выходного сигнала f2(t), т. е., как и в предыдущих случаях, длительность фронта нарастания и спада импульса обратно пропорциональна полосе пропускания цепи w0. Чем уже полоса, тем более затянут фронт импульса; чем меньше длительность импульса, тем шире должна быть полоса пропускания цепи. Обычно на практике полосу пропускания выбирают из условия: SA = 2/tи.

