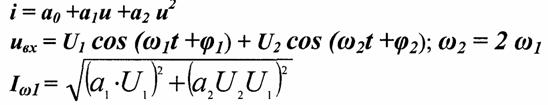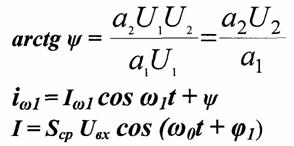
Существуют следующие режимы работы НЭ.
1. Моногармонический режим возбуждения.
2.Биогармонический режим 
3. Полигармонический режим
Для ФУ с Нелинейным элементом существует два случая:
Если 
(
), можно представить в виде отношения небольших чисел, то такой режим называется синхронным режимом возбуждения.
Если (), не возможно представить в виде отношения небольших чисел, то такой режим называется - асинхронный.
В зависимости от выбора аппроксимирующей функции применяют тот или иной метод определения спектральной составляющей (метод спектрального анализа).
1. Аппроксимация полиномом пой степени. i = а0 +a1u +a2 и2 + ... + anun
Используют тригонометрические формулы от кратных аргументов.
2. Аппроксимация ломаной линии: используют метод угла отсечки.
3. Метод трех и пяти ординат, аппроксимация не требуется, спектральные составляющие тока определяются графоаналитическим методом.
4. Аппроксимация экспонентой или сумма экспонент: применяется разложение тока при помощи функции Бесселя от мнимого аргумента.
5. Аппроксимация функцией гиперболического тангенса: разложение в ряд Тейлора.
МЕТОД ПРИМЕНЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФОРМУЛ ОТ КРАТНОГО АРГУМЕНТА.
Этот метод применятся при анализе модуляторов, детекторов, умножителей частоты и т.д.
Рассмотрим действие гармонического сигнала на НЭ, ВАХ которого аппроксимирована полиномом 3ей степени.
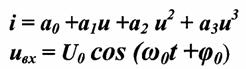Спектральные составляющие тока.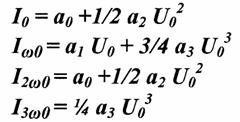 
Наивысший номер гармоники равен в степени аппроксимированного полинома.
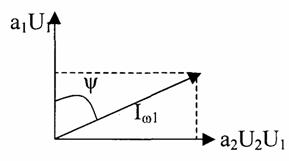
ДЕЙСТВИЕ ДВУХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ С РАЗЛИЧНЫМИ ЧАСТОТАМИ И НАЧАЛЬНЫМИ ФАЗАМИ
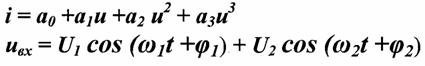
Спектральные составляющие тока.
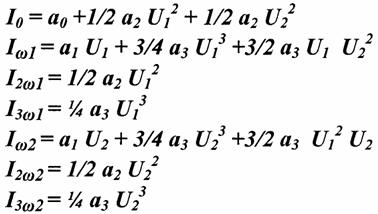Комбинационные частоты: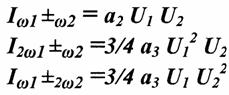 
Комбинационные составляющие характеризуются порядком:
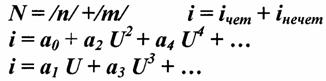
ДЕЙСТВИЕ ДВУХ ГАРМОНИЧЕСКИХ СИГНАЛОВ С КРАТНЫМИ ЧАСТОТАМИ НА НЭ
