3.5.1. Выполнение основных логических операций

3.5.2. Преобразования над цифровыми и аналоговыми картинами

3.5.3. Преобразования в когерентных пучках

3.5.1. Выполнение основных логических операций

Рассмотренные устройства позволяют реализовать разнообразные вычисления и преобразования информации как в аналоговой, так и в цифровой формах. Аналоговая форма обработки привлекательна тем, что всевозможные датчики, приемники и средства отображения физических величин работают в режиме непрерывного изменения входных и выходных сигналов, а цифровая, как уже отмечалось, характеризуется более высокой точностью, надежностью и помехоустойчивостью, поскольку основывается на идентификации легко различимых состояний.

Рассмотрим сначала, как оптическими методами выполняются элементарные логические операции. Будем изображать (рис. 3.11) оптический элемент, пропускающий свет при наличии управляющего сигнала х, незаштрихованным прямоугольником (Т), а элемент, пропускающий свет в отсутствие управляющего сигнала,— заштрихованным прямоугольником (Т). На рис. 3.11 стрелками показаны как управляющие сигналы (х, х₁, х₂), так и управляемый пучок (оптическое «питание»). Оптический сигнал на выходе обозначен у.

В случае, когда оптический пучок проходит последовательно через управляемые элементы Т, реализуется операция логического умножения (у = х₁ ^ х₂, И). В этом легко убедиться на примере устройства с двумя входами (рис. 3.11, а). Свет через устройство не пройдет (у = 0) как при отсутствии обоих управляющих сигналов (х₁ =0, х₂ =0), так и при подаче сигнала только на один из элементов (х₁=l, х₂=0 или х₁=0, х₂ =1); свет попадает на выход (у = 1), только если управляющие сигналы подать и на один, и на другой входы (х₁=l, х₂=1).

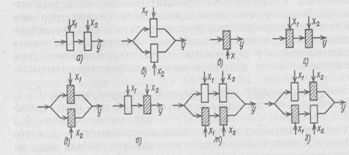
Для выполнения операции логического суммирования (у= х₁х₂, ИЛИ) управляемые оптические элементы Т «включены» параллельно (рис. 3.11, б). В этом случае для попадания света на выход (у = 1) достаточно, чтобы управляющий сигнал был подан хотя бы на один из элементов (х₁=0, х₂ =1 или х₁=l, х₂=0). Разумеется, y=l и при подаче управляющего сигнала на оба элемента (х₁=l, х₂ =1).

Операции инверсии (у = , НЕ выполняется при помощи одного элемента, пропускающего свет в отсутствие управляющего сигнала, т. е. при помощи элемента (рис. 3.11, в). Легко убедиться в том, что если два элемента включить параллельно, реализуется операция И—НЕ (штрих Шеффера, у = х₁↑ х₂ ), а операция ИЛИ — НЕ (стрелка Пирса, у = х₁↓ х₂ )—при их последовательном включении (рис. 3.11, г, д). Если же свет проходит последовательно через элементы Т и , выполняется операция запрета у= х₁← х₂ (рис. 3.11, е). Смысл этого преобразования состоит в том, что при отсутствии запрещающего сигнала (х₂=0) свет проходит через устройство при х₁ =1 и не проходит при х₁ =0. При подаче запрещающего сигнала (х₂ = 1) свет на выход не попадает при любом значении х₁.

На рис. 3.11, ж, з продемонстрировано, как оптическими методами можно выполнить операции равнозначности (у = х₁~ х₂) и неравнозначности (у = х₁ х₂). В этом случае управляющий сигнал х₁, как и х₂, попадает сразу на два оптических элемента Т и . Из рисунка видно, что в схеме равнозначности свет попадает на выход при совпадении состояний входных сигналов, т. е. как при х₁ =0, х₂ =0, так и при х₁ =1, х₂ =1. Если же на один из входов управляющий сигнал подавать, а на другой нет, свет на выходе отсутствует. В схеме неравнозначности, наоборот, свет на выходе попадает при различных состояниях х₁ и х₂ (х₁ =1, х₂ =0 или х₁ =0, х₂=1) и не попадает при одинаковых х₁ и х₂ (х₁ =1, х₂ =1 или х₁ =0, х₂ =0). Комбинируя элементы Т и , можно выполнять и другие преобразования.

3.5.2. Преобразования над цифровыми и аналоговыми картинами

В качестве оптических элементов Т и могут использоваться ячейки матричных оптических транспарантов, управляемых либо оптически, либо электрически. Важно, что при помощи транспарантов можно производить обработку информации сразу по многим каналам параллельно, т. е. выполнять преобразования над картинами. Одна из возможных схем предназначенного для этого оптического процессора (вычислителя) представлена на рис. 3.12.

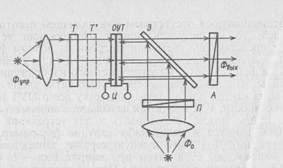
Коллимированный пучок света Ф_упр направляют на ОУТ, работающий на отражение и фиксирующий результат вычислений. В схему считывания ОУТ (при помощи пучка Ф₀) входят скрещенные поляризатор П и анализатор А, так что при отсутствии управляющего оптического сигнала Ф_упр на входе интенсивность света на выходе (Ф_вых) также равна нулю. Этот транспарант должен обладать памятью и, кроме того, позволять за счет изменения режима питания U преобразовывать позитивное изображение в негативное и наоборот (см. § 3.3). На пути пучка Ф_упр помещен работающий на просвет транспарант Т, предназначенный для формирования нужных картин и проецирования их на ОУТ.

Запишем на ОУТ заданное транспарантом Т изображение, а затем, не снимая напряжения U, другое изображение. При считывании окажутся светлыми те места ОУТ, на которые попал управляющий сигнал при проецировании первого, второго, либо того и другого изображений. Очевидно, что таким образом производится операция сложения изображений (картин). Операцию умножения картин можно осуществить, если на пути пучка Ф_упр за транспарантом Т (или перед ним) поместить еще один транспарант Т'. Если транспарантами Т и Т' задать нужные картины, то при их одновременной записи на ОУТ свет попадет только в те его места; против которых прозрачны как Т, так и Т', что и требуется для операции умножения.

Если после записи одного изображения при напряжении U записать другое изображение при напряжении — U (используя один транспарант Т), то произойдет взаимное стирание сигналов в тех местах ОУТ, на которые попал свет при проецировании как одного, так и другого изображений. При считывании (U=0) на выходе сигнал будет присутствовать только в тех местах, на которых свет в одном изображении присутствовал, а в другом нет, или же наоборот. Такому преобразованию соответствует операция вычитания картин.

Изменяя последовательность записи, режим питания ОУТ при записи и считывании, можно выполнять и многие другие преобразования над изображениями. Если, например, из картины, содержащей множество элементов, вычесть такую же, но отличающуюся отсутствием или наличием некоторых новых деталей, то на результирующем изображении те и другие будут представлены светлыми местами на черном фоне. Часто такие «лишние» или «отсутствующие» детали удобнее наблюдать на фоне слабого, малоконтрастного изображения исходной картины, что довольно просто осуществить, вводя при записи одной из картин однородную подсветку всего ОУТ подходящей интенсивности, т. е. вводя так называемое оптическое смещение. Этот прием можно использовать и для устранения фона, если таковой имеется в какой-либо картине (например, вуаль на фотографии). Для этого нужную картину записывают на ОУТ при напряжении U, а затем при напряжении — U производят запись равномерной засветки. При определенной экспозиции засветки фон в результирующей картине исчезнет (разумеется, если фон и засветка строго равномерны).

При помощи процессора, схема которого изображена на рис. 3.12, можно производить пространственное дифференцирование изображений. Для этого нужно записать на ОУТ исходное изображение, а затем вычесть из него изображение той же картины, но несколько сдвинутое или расфокусированное. При этом на результирующей картине на черном фоне будут изображены не сами объекты, а их контуры. Вводя оптическое смещение, можно одновременно наблюдать малоконтрастное изображение исходной картины, детали которой окаймлены светлыми линиями. Польза от такого преобразования становится очевидной, если производить пространственное дифференцирование не цифровой картины, а полутонового изображения. В этом случае на выходе ОУТ черные места останутся черными, белые также станут черными, а проявятся только те места, которые соответствуют наибольшему градиенту освещенности. При помощи такого аналогового преобразования, следовательно, на отображенном объекте можно выделить трудно различимые мелкие детали.

Важные прикладные аспекты имеет использование и других операций над изображениями. Операция умножения, например, может эффективно использоваться для ослабления влияния на изображение мешающих помех. Для этого на транспарантах Т и Т' (рис.3.12) формируются два изображения одного и того же объекта. Если эти изображения содержат случайные помехи (некоррелированный шум), то, производя умножение изображений, т. е. пропуская пучок света последовательно через транспаранты Т и Т' и записывая результирующую картину на ОУТ, на его выходе получают изображение с увеличением соотношения сигнал/шум по сравнению с изображениями на Т и Т'. Некоторые помехи все же пройдут на выход, но только те, пространственное положение которых на транспарантах Т и Т' случайно совпадет.

3.5.3. Преобразования в когерентных пучках

Использование когерентного излучения расширяет и обогащает возможности оптической обработки информации.

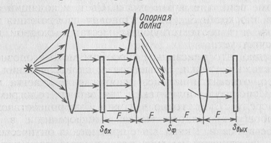
На рис. 3.13 показана упрощенная схема, объясняющая работу оптического процессора с использованием пространственной фильтрации. На плоскость S_BX (входную) направлен параллельный, коллимированный от точечного источника пучок когерентного излучения. Схема включает в себя две сферические собирающие линзы с фокусным расстоянием F, расположенные на расстоянии F и 3F от входной плоскости. Если в плоскости S_BX поместить оптический транспарант (например, ЭУТ), формирующий какую-либо картину Ф_вх, то в соответствии с законами лучевой оптики в плоскости S_вых (выходной или корреляционной) будет воспроизведена картина, перевернутая по отношению к Ф_вх. В плоскости S_ф, которую называют частотной или плоскостью фильтрации, сформируется распределение амплитуды и фазы светового поля, пропорциональное спектру пространственных частот картины Ф_вх (будет выполнено преобразование Фурье функции Ф_вх). Любой транспарант, помещенный в плоскости S_ф, по существу выполняет функцию пространственного фильтра. Экран с прямоугольным отверстием, например, является двумерным пространственным фильтром нижних частот, непрозрачный прямоугольник — двумерным фильтром высоких частот, узкая щель—одномерным пространственным фильтром низких частот и т. д. Привлекательно применение в качестве пространственного фильтра ЭУТ, что позволяет производить фильтрацию, изменяющуюся во времени.

Практически недоступные для ЭВМ возможности открывает использование в системах оптической обработки информации голографических методов. Введение в плоскость S_ф голограмм позволяет анализировать пространственный спектр картины, сформированной во входной плоскости S_BX, в частности решать такую важную прикладную задачу, какой является распознавание образов.

Выделение нужного объекта включает в себя предварительное изготовление так называемого согласованного фильтра и последующую идентификацию объекта в массиве информации, поступающей на входную плоскость процессора. Предположим, что на странице текста необходимо опознать и определить координату какого-либо знака, например цифры или буквы. Для изготовления согласованного фильтра во входной плоскости S_BX помещают транспарант с изображением этого знака. В плоскости S_ф сформируется световая волна, соответствующая его пространственному спектру. Если при помощи светоделителя и зеркал на плоскость S_ф одновременно направить опорную волну, когерентную с волной, освещающей входную плоскость S_BX (схема Вандер Люгта), то в плоскости S_ф образуется интерференционная картина, представляющая собой голограмму Фурье-образа объекта, помещенного в плоскости S_ВХ. Зафиксированная голограмма и представляет собой согласованный фильтр пространственных частот этого объекта. Эта голограмма содержит амплитудную и фазовую информацию о знаке, который изображен на входе, и ее можно использовать для распознавания данного знака. Для этого голограмму-фильтр оставляют в плоскости S_ф, убирают опорную волну, а в плоскости S_BX помещают страницу с текстом, осветив ее тем же источником света. Голографический метод распознавания образов основывается на том, что если голограмму восстанавливать излучением объекта, который использовался при ее регистрации, т. е. его световое поле использовать в качестве считывающей волны, то при этом будет восстановлено изображение используемого точечного источника. В выходной плоскости S_ВЫХ, следовательно, в местах, соответствующих изображению заданного знака, появятся изображения источника света, т. е. яркие пятна. Свет, исходящий от других знаков в плоскости S_BX, не восстановит изображения точечного источника и в соответствующих местах выходной плоскости свет отсутствует.

Очевидно, что описанным способом можно опознать сколь угодно сложные знаки, целые слова, словосочетания, рисунок, например, отпечатки пальцев, изображение участка местности и т. д. Используя, опять-таки, для записи голограмм реверсивную среду с достаточно высоким быстродействием, можно вести обработку целого массива информации в реальном масштабе времени. Уникальные применения оптических процессоров рассматриваемого типа открываются, если использовать возможность синтеза пространственно-частотных фильтров при помощи ЭВМ.