Для нахождения реакции нелинейной электрической цепи с нелинейным двухполюсником или четырехполюсником на заданное воздействие можно использовать графические построения. Статические характеристики нелинейного прибора, т. е. зависимость между воздействием и реакцией на его внешних зажимах для режима постоянного тока, считаются известными. Ими могут быть, например, вольт-амперная характеристика нелинейного резистора, или зависимость между постоянными напряжениями на входе и выходе нелинейного четырехполюсника и др. Эти характеристики находятся, как правило, в результате измерений и представляются в виде графических зависимостей, что и оправдывает использование графических методов решения рассматриваемой задачи.

В основе метода лежит предположение о том, что в любой момент времени реакция нелинейного прибора на подведенное к нему воздействие будет такой же, как и его реакция на постоянное воздействие той же величины. Иными словами, предполагается, что модель анализируемой цепи является моделью резистивной электрической цепи. Ниже на примере рассматривается методика графического нахождения реакции нелинейного прибора с однозначной характеристикой нелинейности.

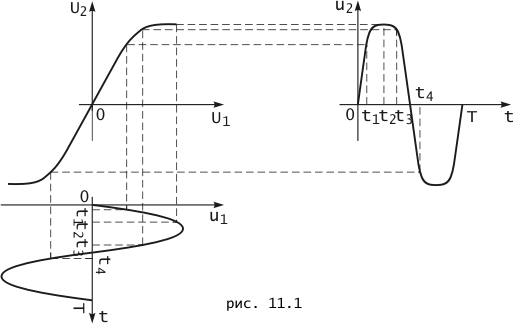
Рассмотрим зависимость постоянного напряжения U ₂ на выходе нелинейного четырехполюсника от постоянного напряжения U ₁, подведенного к его входу. Ее график U ₂ = U ₂(U ₁) показан па Рис. 11.1 рис. 11.1. На этом же рисунке, приведен график воздействия u ₁(t). Он повернут на угол по часовой стрелке по сравнению с общепринятым графическим изображением функции времени. Воздействие в примере тождественно равно нулю вне интервала 0 < t < T, внутри которого оно описывается функцией u ₁(t) = U _msin(2 pt /T).

В момент времени t = t ₁ ко входу нелинейного прибора, как это следует из рис. 11.1., подводится напряжение u ₁(t ), т. е. при t = t₁ : U₁ = u ₁ (t ₁ ). Напряжение на его выходе, которое находится по графику U ₂ (U ₁ ), т. е. напряжение U ₂ при U₁ = u ₁ (t ₁ ) и будет напряжением реакции u ₂ (t ₁ ) нелинейного при6oрa в момент времени t ₁ . Значение реакции отложено на графике u ₂ (t), приведенном на том же рисунке. Отсчетные значения u₁ (t₁ )и u₂ (t₁ ) соединены на рис. 11.1. штриховой линией. Аналогичные построения приведены на рисунке и для трех других моментов времени t = t₂ , t = t₃ , t = t₄ . В результате подобных построений и находится график реакции u₂ (t).

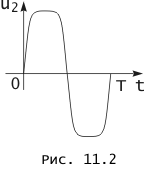
Сопоставление графиков воздействия u ₁(t ) и реакции u ₂(t ), приведенных на рис. 11.1., показывает, что они отличаются друг от друга формой. Следовательно, в рассматриваемой нелинейной электрической цепи произошло искажение формы реакции по сравнению с формой воздействия, обусловленное нелинейностью характеристики используемого нелинейного прибора. Из тех же графиков следует, что указанные искажения уменьшаются с уменьшением амплитуды воздействия и для любого t при условии | u₁ (t)| < u₁ (t₁ ), зависимость реакции от воздействия будет близка к линейной. Итак, анализируемую цепь в ряде случаев можно рассматривать как линейную электрическую цепь и с тем большим основанием, чем меньше амплитуда воздействия. Наоборот, с увеличением амплитуды воздействия заметнее отличия формы реакции от формы воздействия. В частности, значение реакции u ₂(t) по абсолютной величине практически не зависит от воздействия, если | u₁ (t)| > u₁ (t₂ ) (см. рис. 11.1. ), а при | u ₁ (t)| = u ₁ (t ₂ ) реакция принимает вид двух трапецеидальных импульсов различной полярности. Ее график показан на рис. 11.2.

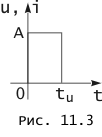
Искажение формы реакции относительно формы воздействия свойственно электрическим цепям и с другими характеристиками нелинейности, отличающимися от рассмотренных в примере, в том числе и многозначными. Вместе с тем в рассматриваемых резистивных нелинейных цепях не искажается форма воздействия в виде импульса прямоугольной формы, график которого приведен на рис. 11.3. Здесь нелинейность проявляется в отсутствии прямой пропорциональности между амплитудами реакции и воздействия, а при больших амплитудах воздействия – в независимости их друг от друга.

Естественно, что если характеристика нелинейности задана аналитически, то реакция нелинейного прибора на заданное воздействие может быть найдена и в результате численного решения нелинейного уравнения, связывающего мгновенные значения реакции и воздействия в выбранной совокупности дискретных моментов времени.