Характеристическое уравнение

Операторный метод анализа автогенератора состоит в исследовании характеристического уравнения (14.11) цепи с ОС и выявлении из этого уравнения условий самовозбуждения. Записать характеристическое уравнение генератора можно было бы непосредственно по дифференциальному уравнению (15.9), однако это можно сделать и не прибегая к составлению дифференциального уравнения. Генератор как цепь с ОС описывается характеристическим уравнением:

Операторная передаточная функция такого усилителя равна:

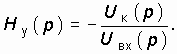
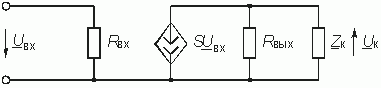
В свою очередь, из рис. 15.11 следует, что

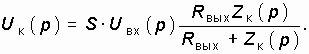
Поэтому

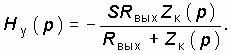
На практике в качестве усилительного элемента используют такой транзистор, у которого R_вых достаточно велико. В этом случае

Учитывая, что сопротивление параллельного контура

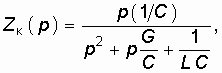
получаем окончательное выражение передаточной функции усилителя

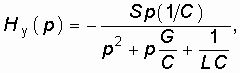
Передаточную функцию цепи ОС легко найти, если вспомнить, что

или для изображений по Лапласу

Отсюда

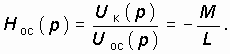
После того, как получены выражения для Н_у(р) и Н_ос(р), характеристическое уравнение (15.14) можно записать в следующем виде:

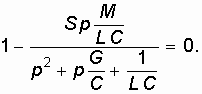
После простейших преобразований получим:

или

В режиме самовозбуждения рабочая точка располагается на линейном участке ВАХ и, следовательно, крутизна S является постоянной величиной.

Корни характеристического уравнения (15.16)

где – частота свободных колебаний в контуре.

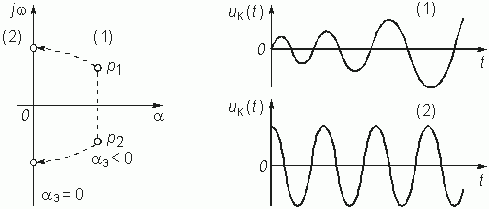
Чтобы в генераторе возникли незатухающие колебания корни должны лежать в правой полуплоскости комплексной переменной р (рис. 15.12, случай 1), т. е. a _э < 0. Таким образом, условие самовозбуждения примет вид M > LG/ S, что совпадает с выражением (15.10).

В стационарном режиме работы генератора корни перемещаются на мнимую ось комплексной плоскости р (рис. 15.12, случай 2). Из условия a _э = 0 можно найти стационарное значение средней крутизны:

Анализ в частотной области

Заменяя в выражениях для операторных передаточных функций оператор р на оператор jw , запишем передаточную функцию цепи с разомкнутой ОС:

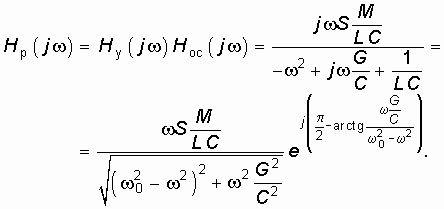
Из условия баланса фаз на частоте генерации

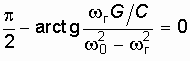
убеждаемся, что генератор возбуждается на частоте w _г = w ₀.

Из условия баланса амплитуд, которое должно выполняться на частоте генерации

находим, что самовозбуждение происходит при M > LG/ S, что совпадает с полученными ранее результатами.

Баланс амплитуд на частоте генерации позволяет определить стационарное значение средней крутизны

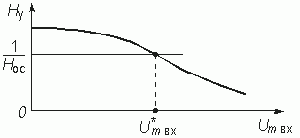
Можно построить зависимость Н_у на частоте генерации от стационарной амплитуды колебаний U_m.. (рис. 15.13). Функцию Н_у(U_m..) легко получить из формулы (15.15), зная среднюю крутизну S_ср(U_m..) и сопротивление контура на частоте генерации Z_к(w _г) = 1/G:

.

В стационарном режиме выполняется условие

Воспользовавшись этим условием, можно найти стационарную амплитуду колебаний на входе усилителя, как это сделано на рис. 15.13. Стационарная амплитуда колебаний на выходе генератора определяется по формуле