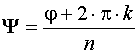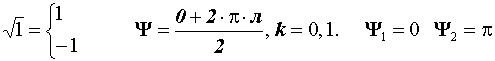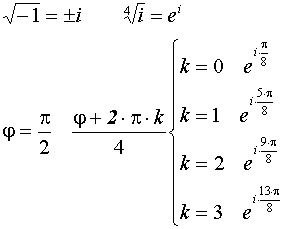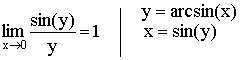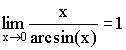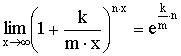1.2. Функция, способы задания, простейшие свойства
1.1. Комплексные числа (КЧ)
Комплексным числом z называется выражение z = a+bi, где ![]() , i – мнимая единица. i 2 = –1.
, i – мнимая единица. i 2 = –1.
a – действительная часть КЧ или a = Re z.
b – мнимая часть КЧ или b = Im z.
0+bi = bi - чисто мнимое число
a + 0i = a - действительное число
|
0 + 1i = i |
1 + 0i = 1 |
0 + 0i = 0 |
|
мнимая единица |
обычная единица |
обычный нуль |
Z1 = a1 + b1i
Z2 = a2 + b2i
![]()
Действия над КЧ
Z1 ![]() Z2 = (a1
Z2 = (a1 ![]() a2) + (b1
a2) + (b1 ![]() b2)
b2)![]() i – сложение/вычитание КЧ.
i – сложение/вычитание КЧ.
Возведение в степень мнимой единицы:
i1 = i i2 = – 1 i3 = i i4 = 1
Z1 ![]() Z2 = (a1 + b1
Z2 = (a1 + b1![]() i)
i)![]() (a2 + b2
(a2 + b2![]() i) = a1
i) = a1![]() a2 + a1
a2 + a1![]() b2
b2![]() i
i
+ a2![]() b1
b1![]() i
i
+ b1![]() b2
b2![]() i2 =
i2 =
= (a1![]() a2 – b1
a2 – b1![]() b2) + (a1
b2) + (a1![]() b2 + a2
b2 + a2![]() b1)
b1)![]() i – произведение КЧ.
i – произведение КЧ.
Сопряженным числом (![]() ) для данного комплексного числа называется число, которое отличается только знаком мнимой части от данного числа.
) для данного комплексного числа называется число, которое отличается только знаком мнимой части от данного числа.
![]()
Пример: ![]()
![]()
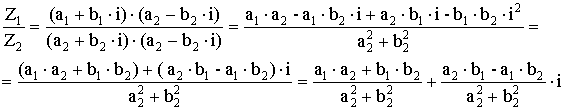 – деление КЧ.
– деление КЧ.
Пример:
![]()
Комплексная плоскость
Z = a + bi – алгебраическая форма записи КЧ.
Модуль КЧ
![]()
Аргумент КЧ
Аргумент КЧ – ![]() .
.
Полярная система координат
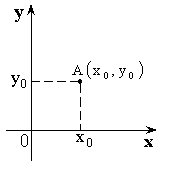
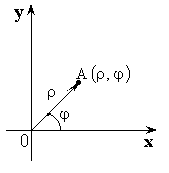
Декартова система. Полярная система
![]() – полярный радиус,
– полярный радиус, ![]() – полярный угол,
– полярный угол, ![]() – полярные координаты.
– полярные координаты.
![]()
![]()
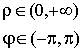
![]() ;
; ![]()
![]()
Пример:
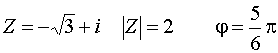
![]()
![]() – тригонометрическая форма записи КЧ.
– тригонометрическая форма записи КЧ.
Примеры:
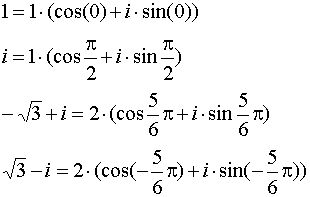
Формула Эйлера
|
|
– Формула Эйлера |
|
|
|
– взаимосвязь между e, i и |
![]() – показательная форма КЧ.
– показательная форма КЧ.
![]()
КЧ не сравнивают между собой. Множество КЧ не упорядоченно.
Возведение в степень КЧ
![]()
При возведении в степень модуль возводиться в эту степень, а аргумент умножается на показатель степени.
Формула Муавра
![]()
Возведение во 2 – ю и 3 – ю степень по формуле Муавра:
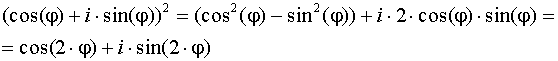
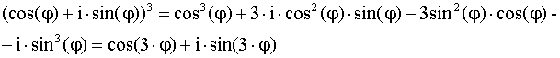
Используя равенство КЧ, получим: 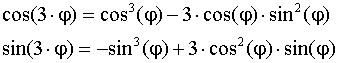 s
s
Извлечение корня из КЧ
![]()
![]()
![]()
![]()
|
|
k = 0, 1…,n – 1. |
Корень n – ой степени из КЧ имеет n различных значений.
Примеры:
Все корни n-ой степени из единицы находятся на единичной окружности и делят эту окружность на n равных частей.
1.2. Функция, способы её задания, простейшие свойства
Основные обозначения:
N – натуральные числа,
Q – рациональные(дробные),
Z – целые числа,
R – действительные числа;
![]()
Счетное множество – это множество, элементы которого можно пересчитать.
![]() – счетные и имеют одинаковую мощность
– счетные и имеют одинаковую мощность
R – несчетное множество.
 Множество действительных чисел всюду плотно на числовой оси.
Множество действительных чисел всюду плотно на числовой оси.
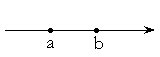 [a, b] – замкнутый интервал, (a, b) – открытый интервал
[a, b] – замкнутый интервал, (a, b) – открытый интервал
Окр [x0] – окрестность точки x0 , любой открытый интервал, содержащий x0.
Окр [x0] = (a, b), где (a, b) содержит x0 – это окрестность.
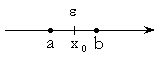 ax0 = x0b,
ax0 = x0b, ![]() – окрестность x0
– окрестность x0
Кванторы
1) ![]() – кванты всеобщности;
– кванты всеобщности;
2) ![]() – кванты существования.
– кванты существования.
|x – x0| – расстояние от точки x до точки x0
Числовой функцией называется соответствие между числовыми множествами X![]() Y, при котором каждому значению x соответствует (сопоставлено) некоторое значение y.
Y, при котором каждому значению x соответствует (сопоставлено) некоторое значение y.
![]()
![]()
![]()
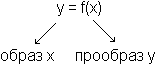
У каждого прообраза всегда один образ, у каждого образа может быть много прообразов.
Взаимнооднозначная функция – это когда разные x имеют разные y.
Способы задания функций:
а) аналитический;
б) графический;
в) табличный;
г) алгоритмический.
Функции делятся на 2 класса
- Элементарные
- Неэлементарные (специальные).
Элементарные функции изучаются в школьной математике и делятся на:
- Основные элементарные функции
а) степенные y = xn
б) показательные y = ax
в) тригонометрические y = sin x и другие.
- Элементарные, полученные из основных с помощью арифметических операций и операции получения сложной функции (операции композиции).
f
X Y
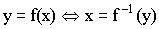
f -1 (обратная функция)
Обратные к показательным функциям – логарифмические функции. Обратные к тригонометрическим
Пример:
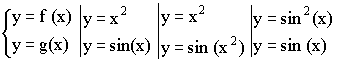
y = f (g(x)) – сложная функция – композиция элементарных функций.
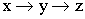
Элементарными функциями называются функции, полученные из элементарных базисных функций с помощью алгебраических операций и операций композиции.
Г(f) – график функции. График функции есть множество точек (x, y), где y = f(x).
Общие свойства функций
- Четность –
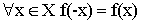
- Нечетность –
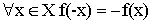
- Периодичность –
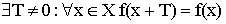
f(x) – ограниченная сверху, если ![]()
f(x) – ограниченная снизу, если ![]()
f(x) – ограниченная, если ![]()
f(x) – монотонная, если она постоянно возрастает или постоянно убывает
Если y = f(x), то Д – область определения данной функции.
Свойства модулей суммы и разности
1.3. Предел функции. Свойства пределов
Число b называется пределом функции в точке а, если для любой ![]() – окрестности точки b существует
– окрестности точки b существует ![]() – окрестность точки а.
– окрестность точки а.
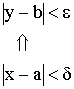
![]()
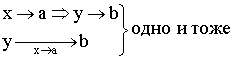
![]() – предел функции при
– предел функции при ![]() , равный b.
, равный b.
Число b называется пределом функции при неограниченном возрастании аргумента ![]() .
.
Для любого ![]() существует такое N, и если
существует такое N, и если ![]() , то
, то ![]() .
.
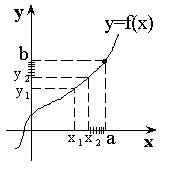
Примеры:
y = f(x) = ![]()
![]()
y = f(x) = x2 ![]()
Пример:
y =![]() , когда
, когда ![]() ,
, ![]()
Неопределенности: 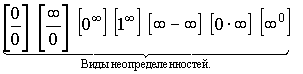
Раскрытие неопределенностей.
Теорема об ограниченности функции, имеющей предел
Если функция f(x) имеет предел в точке a ![]() , то она ограниченна в некоторой окрестности точки a.
, то она ограниченна в некоторой окрестности точки a.
Доказательство:
Пусть ![]() , тогда
, тогда ![]() , отсюда получаем
, отсюда получаем ![]() .
.
Обратное неверно.
Контрольный пример:
![]() в окрестности точки 0.
в окрестности точки 0.
![]() – не существует.
– не существует.
Бесконечно малой величиной при ![]() называется функция, предел которой в точке a равен 0.
называется функция, предел которой в точке a равен 0.
![]()
![]() – бесконечно малая величина (б.м.в.).
– бесконечно малая величина (б.м.в.).
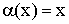 – бесконечно малая величина при
– бесконечно малая величина при 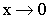
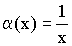 – бесконечно малая величина при
– бесконечно малая величина при 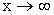
s
Бесконечно большой величиной при ![]() называется функция неограниченно возрастающая.
называется функция неограниченно возрастающая.
![]()
![]() – бесконечно большая величина (б.б.в.)
– бесконечно большая величина (б.б.в.)
Любая бесконечно большая величина неограниченна.
Теорема о связи предела и бесконечно малой величины
Если ![]() , то
, то ![]() , где
, где ![]() – бесконечно малая величина. Или
– бесконечно малая величина. Или ![]() .
.
Доказательство:
Допустим, что ![]() , тогда
, тогда 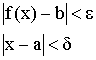 .
.
![]() , значит
, значит ![]() ,
, ![]() – бесконечно малая величина.
– бесконечно малая величина.
Пример:
f(x) = x2 + 1
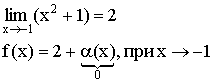
Теорема о связи бесконечно малой и бесконечно большой величиной
Если ![]() – бесконечно малая величина при
– бесконечно малая величина при ![]()
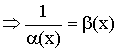 – бесконечно большая величина.
– бесконечно большая величина.
Если ![]() – бесконечно большая величина при
– бесконечно большая величина при ![]()
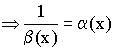 – бесконечно малая величина.
– бесконечно малая величина.
Доказательство:
Допустим, что ![]() – бесконечно малая величина при
– бесконечно малая величина при ![]() , то
, то ![]() , что
, что ![]() .
.
Значит ![]()
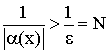
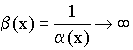
Следствие: 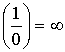 и
и 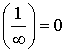
Свойства бесконечно малых величин
1) Алгебраическая сумма бесконечно малых величин есть бесконечно малая: ![]()
Доказательство:
![]()
![]() или
или ![]() , значит
, значит ![]() – бесконечно малая величина.
– бесконечно малая величина.
2) Произведение бесконечно малой величины на ограниченную функцию есть бесконечно малая: ![]() , где f(x) – ограниченная.
, где f(x) – ограниченная.
Доказательство:
![]()
![]() , значит
, значит ![]() – бесконечно малая величина.
– бесконечно малая величина.
3) Частное от деления бесконечно малой величины на любую функцию, предел которой не равен 0, есть бесконечно малая: 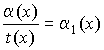 при
при ![]() и
и ![]() .
.
Теоремы о пределах
Теорема 1. Предел суммы равен сумме пределов, если они существуют: ![]()
Доказательство:
![]()
![]()
Из теоремы о связи между пределом и бесконечно малой величиной следует:
![]()
![]()
![]()
Получаем ![]()
![]()
Теорема 2. Предел произведения равен произведению пределов, если они существуют: ![]()
Доказательство:
![]()
![]()
Из теоремы о связи между пределом и бесконечно малой величиной следует:
![]()
![]()
![]()
Получаем ![]()
![]()
![]()
Теорема 3. Предел частного равен частному пределов: 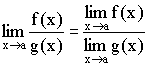 .
.
При условии: все пределы существуют и ![]() .
.
Доказательство:
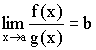
![]()
Из теоремы о связи между пределом и бесконечно малой величиной следует:
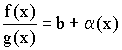
![]() ;
;
Получаем: 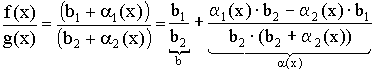
![]()
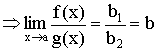
Теорема 4. Предел сохраняет знак неравенства. Если ![]()
![]() .
.
Доказательство:
![]()
Следовательно, ![]()
![]()
Следствие:
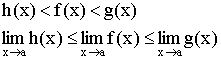
Теорема 5. Если функция ограниченна и монотонна на (a, b), то она имеет предел: ![]()
Теорема 6. Критерий Коши.
Если ![]() , тогда и только тогда
, тогда и только тогда ![]() .
.
Приемы раскрытия неопределенностей.
1) Выделение общего множителя (для неопределенности ![]() ).
).
Пример:
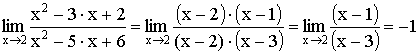
2) Умножение на сопряженное выражение (для неопределенности ![]() ).
).
Пример:
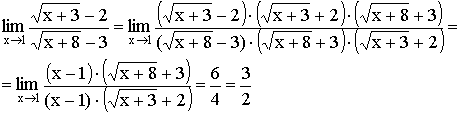
3) Выделение главной части (для неопределенности ![]() ).
).
Примеры:
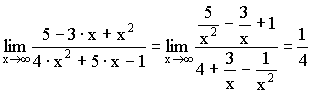
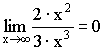 ;
;
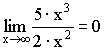
Теорема. Первый замечательный предел ![]() .
.
Доказательство (геометрическое):
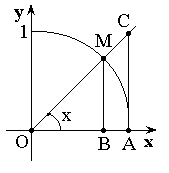
![]()
![]()
![]()
![]()
![]()
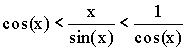
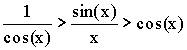
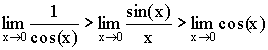
Так как 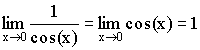 ,
,
то ![]() .
.
Следствия из теоремы:
1)
2)
3)
4)
5)
Теорема. Второй замечательный предел 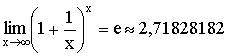 .
.
Доказательство:
Бином Ньютона:
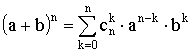 ,
,
где 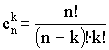 .
.
Используем бином Ньютона для доказательства неравенства: 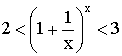
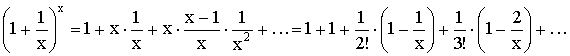
Отсюда заключаем, что 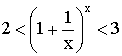 ,
,
а значит 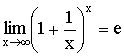 .
.
Следствия из теоремы:
1)
2)
3)
4)
Доказательство:
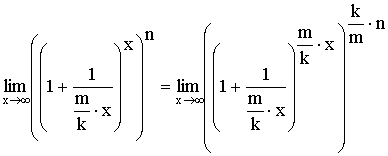
Если принять, что ![]() ,
,
то 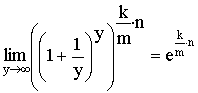
Примеры:
1) 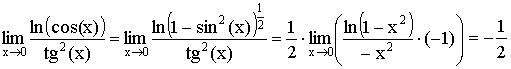
Учитывая, что ![]() .
.
2) ![]()
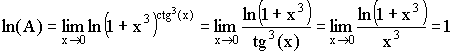 . Отсюда A = e.
. Отсюда A = e.
Учитывая, что ![]() .
.
Сравнение бесконечно малых величин (б.м.в.)
Пусть ![]() – бесконечно малые величины при
– бесконечно малые величины при ![]() , т.е.
, т.е. ![]() .
.
Определение 1. Если 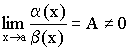 , то
, то ![]() – б.м.в. одного порядка малости.
– б.м.в. одного порядка малости.
Определение 2. Если 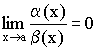 , то
, то ![]() – б.м.в. более высокого порядка, чем
– б.м.в. более высокого порядка, чем ![]() .
.
![]() –
– ![]() более высокого порядка, чем
более высокого порядка, чем ![]() ("о" – читается как "о малое").
("о" – читается как "о малое").
![]() –
– ![]() более низкого порядка, чем
более низкого порядка, чем ![]() ("О" – читается как "О большое").
("О" – читается как "О большое").
Определение 3. Если 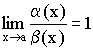 , то
, то ![]() и
и ![]() эквивалентны –
эквивалентны – ![]() .
.
Следствие из определения 3: ![]() при
при ![]() .
.
Теорема. Если ![]() и
и ![]() эквивалентны (
эквивалентны (![]() ), то
), то ![]() и
и ![]() .
.
Доказательство:
Пусть ![]() – бесконечно малые величины при
– бесконечно малые величины при ![]() и они эквивалентны (
и они эквивалентны (![]() ).
).
Тогда 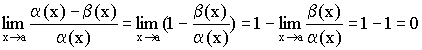 .
.
1.4. Непрерывность функции в точке и на интервале
Определение 1.
Пусть функция ![]() определена в окрестности точки
определена в окрестности точки ![]() , тогда функция непрерывна в
, тогда функция непрерывна в ![]() , если
, если ![]() .
.
Определение 2.
Функция ![]() непрерывна, если
непрерывна, если![]() .
.
Определение 3.
Функция ![]() непрерывна в точке
непрерывна в точке ![]() , если
, если ![]() .Приращение аргумента
.Приращение аргумента ![]() . Приращение функции
. Приращение функции ![]() .
.
Определение 4. Функция ![]() непрерывна в точке
непрерывна в точке ![]() , если
, если ![]() .Если функция не является непрерывной в точке
.Если функция не является непрерывной в точке ![]() , то эта точка – точка разрыва. Если функция непрерывна на отрезке (a, b), то функция неразрывна на отрезке (a, b).
, то эта точка – точка разрыва. Если функция непрерывна на отрезке (a, b), то функция неразрывна на отрезке (a, b).
Определение 5.
Функция ![]() непрерывна в точке
непрерывна в точке ![]() справа, если
справа, если ![]() .
.
Определение 6.
Функция ![]() непрерывна в точке
непрерывна в точке ![]() слева, если
слева, если ![]() .
.
Функция непрерывна на отрезке ![]() , если она непрерывна в каждой внутренней точке этого отрезка и односторонне непрерывна на его концах.
, если она непрерывна в каждой внутренней точке этого отрезка и односторонне непрерывна на его концах.
Теоремы о непрерывных функциях
Теорема 1. Сумма, произведение и частное непрерывных функций – непрерывны (кроме случая, когда знаменатель обращается в нуль).
Доказательство:
Пусть ![]() и
и ![]() .
.
Тогда ![]() .
.
Доказательство для умножения и деления аналогично доказательству для сложения.
Теорема 2. Композиция непрерывных функций непрерывна:
Функция ![]() непрерывна в точке
непрерывна в точке ![]() , если g(x) непрерывна в точке
, если g(x) непрерывна в точке ![]() и f(y) непрерывна в
и f(y) непрерывна в ![]() .
.
Теорема 3. Все элементарные функции непрерывны в своей области определения.
Разрывы функции
Разрыв первого рода
Пусть ![]() и
и ![]() существуют:
существуют:
I. Если ![]() , то в точке
, то в точке ![]() функция
функция
испытывает разрыв скачок первого рода.
Примеры:
-
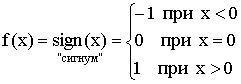
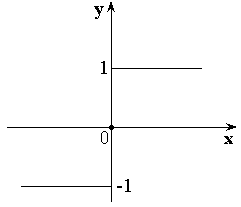
 – целая часть числа x.
– целая часть числа x.
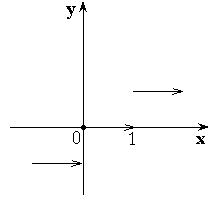
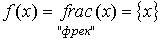 – дробная часть от числа x.
– дробная часть от числа x. 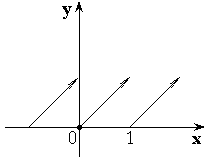
II. Если ![]() , то в точке
, то в точке ![]() функция испытывает устранимый разрыв первого рода.
функция испытывает устранимый разрыв первого рода.
Примеры:
1) 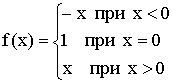
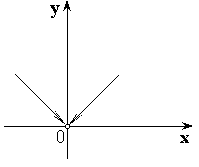
2) 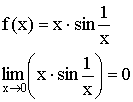
3) 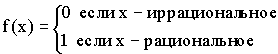
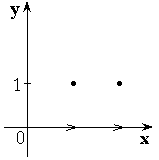
4) 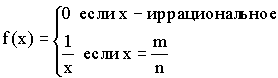
Разрыв второго рода
Функция испытывает разрыв второго рода, если ![]() – не существует.
– не существует.
Свойства функции, непрерывной на замкнутом отрезке
Пусть функция ![]() непрерывна на замкнутом отрезке
непрерывна на замкнутом отрезке ![]() .
.
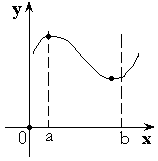
Теорема 1. Функция принимает наибольшее и наименьшее значение на ![]() .
.
Или ![]() , где
, где ![]() .
.
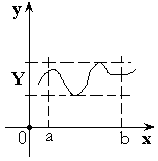
Теорема 2. Функция принимает все свои промежуточные
значения на ![]() .
.
Или ![]() , где
, где ![]() – область значений.
– область значений.
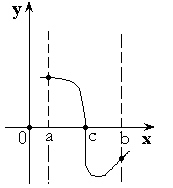
Теорема 3. Если функция принимает на концах отрезка ![]() значения разных знаков, то внутри отрезка найдется точка, в которой
значения разных знаков, то внутри отрезка найдется точка, в которой ![]() .
.
Или ![]() .
.