1. Взаимные влияния в линиях связи

1.1. Проблема электромагнитной совместимости в линиях связи

1.2. Основные определения и методы исследования взаимных влияний

1.3. Влияния в однородных симметричных линиях связи

1.4. Влияние между цепями симметричных кабельных линий связи

1.5. Влияния в строительных длинах кабеля

2. Кабельные линии связи

2.1. Классификация кабелей связи

2.2. Конструктивные элементы кабелей связи

2.2.1. Токопроводящие жилы

2.2.2. Изоляция

2.2.3. Скрутка кабельных цепей

2.2.4. Защитные оболочки и покровы

2.3. Маркировка кабелей связи

2.3.1. Междугородные коаксиальные кабели

2.3.2. Междугородные симметричные кабели

2.3.3. Зоновые (внутриобластные) кабели

3. Коаксиальные кабели

3.1. Электрические процессы в коаксиальных цепях

3.2. Первичные параметры коаксиальной цепи

3.3. Вторичные параметры передачи коаксиальной цепи

4. Симметричные кабели

4.1. Электрические процессы в симметричных цепях

4.2. Емкость и проводимость изоляции симметричной цепи

5. Теория передачи по линиям связи

5.1. Исходные положения

5.2. Уравнения однородной линии

5.3. Волновое сопротивление

5.4. Коэффициент распространения

5.5. Скорость распространения электромагнитной энергии по цепям связи

1. Взаимные влияния в линиях связи

1.1. Проблема электромагнитной совместимости в линиях связи

Цепи и тrакты линий связи постоянно находятся под воздействием сторонних электромагнитных полей того или иного происхождения. Различают две основные группы источников сторонних полей: внешние энергетически и конструктивно не связанные с линией связи – и внутренние – соседние физически и искусственные цепи данной линии связи.

Внешние источники помех по своему происхождению делятся на:

• естественные – грозовые разряды, солнечная радиация, космическое излучение, магнитные бури;

• созданные человеком – высоковольтные линии передачи, радиостанции различного назначения, линии электрифицированных железных дорог, метро и трамвая, электрические сети промышленных предприятий и отдельных энергоемких устройств.

Сторонние электромагнитные поля индуцируют в цепях и трактах линий связи помехи, которые не только снижают качество передачи, но иногда возбуждают большие напряжения и токи, приводящие к разрушению линий связи и аппаратуры, а также создающие опасность для жизни и здоровья эксплуатационного персонала. Поэтому для оценки свойств линий связи помимо изучения законов передачи сигналов необходимо также исследование процессов, связанных с воздействием сторонних электромагнитных полей на линии связи и методы защиты. Указанные воздействия называют электромагнитными влияниями или просто влияниями на цепи линий связи.

Данная проблема является общей для всех систем и устройств, связанных с генерацией, передачей, приемом и обработкой электрических сигналов и называется проблемой электромагнитной совместимости. Сущность ее состоит в том, что в процессе проектирования, строительства и эксплуатации вышеуказанных устройств и систем необходимо учитывать, с одной стороны, воздействие на них сторонних электромагнитных полей заданного характера и обеспечить достаточную для их нормальной работы защиту от этих воздействий, а с другой – предусмотреть мероприятия по ограничению уровней влияния электромагнитных полей проектируемых устройств и систем на другие устройства допустимыми значениями.

В большинстве случаев можно выделить следующие основные этапы решения данной проблемы:

• анализ характера сторонних электромагнитных полей и зависимостей параметров их источников от различных факторов (состояния внешней среды, режима работы источников излучений, их конструкции, времени и т. д.);
• исследование (теоретическое и экспериментальное) законов индуцирования помех, определение их интенсивности, спектральных и временных характеристик, а также степени воздействия на качество передачи информации по линиям связи для различных типов линий связи и систем передачи;
• разработка и анализ эффективности мер защиты цепей и трактов от влияния сторонних электромагнитных полей и их оптимизация по заданным критериям (стоимости, эффективности, надежности и др.); при этом рассматриваются как меры по уменьшению интенсивности влияющих полей, так и меры защиты цепей и трактов, подверженных влиянию;
• выбор (или разработка) мер защиты линий связи от мешающих или опасных влияний сторонних электромагнитных полей, создаваемых внешними и внутренними источниками;
• реализация мер защиты, теоретическое и экспериментальное исследование их эффективности и соответствия максимального уровня помех нормативным значениям.

1.2. Основные определения и методы исследования взаимных влияний

В теории взаимных влияний между цепями линий связи приняты следующие основные определения:

• влияющая цепь – цепь, создающая первичное электромагнитное поле (рис.1);

• цепь, подверженная влиянию – цепь, на которую воздействует влияющее электромагнитное поле и в которой определяются помехи;

• ближний конец линии (кабеля, цепи, тракта) – конец линии, на котором включен генератор влияющей цепи;

• дальний конец линии (кабеля, цепи, тракта) – конец линии, на котором включена нагрузка влияющей цепи;

• непосредственные (прямые) влияния – помехи, индуцируемые цепи в цепи, подверженной влиянию;

• косвенные влияния – помехи, индуцируемые в цепи, подверженной влиянию, вторичными полями влияющей цепи и слагающиеся из влияний от отражений и третьих цепей;

• влияния от отражений – помехи, обусловленные отраженными от концевых, стыковых и внутренних неоднородностей электромагнитными полями в цепях 1 и 2 (рис.2,а);

• влияния через третьи цепи – помехи, индуцируемые вторичными электромагнитными полями, возникающими под воздействием поля влияющей цепи в третьих физических и искусственных цепях линии (рис.2,б);

• влияния, индуцируемые по закону ближнего конца линии – помехи, наводимые в цепи, подверженной влиянию, и распространяющиеся встречно (обратно) направлению передачи сигналов во влияющей цепи (рис.2,в);

• влияния, индуцируемые по закону дальнего конца линии – помехи, наводимые в цепи, подверженной влиянию, и распространяющиеся в направлении передачи сигналов во влияющей цепи (рис.2,в);

• влияния на ближнем конце цепи (тракта) – влияния, определяемые суммарной мощностью помех на ближнем конце цепи, подверженной влиянию (рис.1);

• влияния на дальнем конце цепи (тракта) – влияния, определяемые суммарной мощностью помех на дальнем конце цепи, подверженной влиянию.

Рис. 1

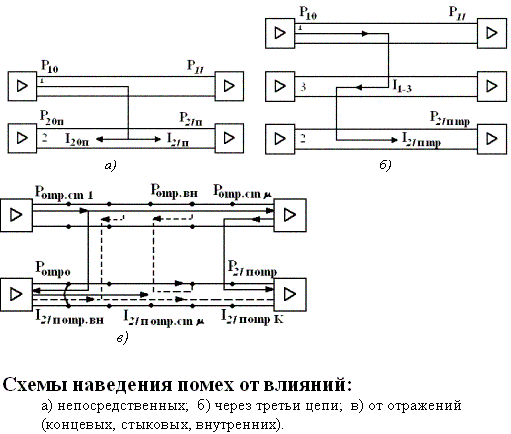
Рис. 2

На рис.1 обозначены мощности, напряжения и токи сигналов и помех на ближнем и дальнем концах влияющей цепи в цепи, подверженной влиянию линии связи, работающих в квазистационарном режиме:

Ρ₁₀(ω), U₁₀(ω), ²₁₀(ω) – мощность, напряжение и ток сигнала на ближнем конце влияющей цепи соответственно на частоте ω;

Ρ_1l(ω), U_1l(ω), ²_1l(ω) – то же, на дальнем конце влияющей цепи;

Ρ₂₀(ω), U₂₀(ω), ²₂₀(ω) – то же, на ближнем конце цепи, подверженной влиянию;

Ρ_20п(ω), U_20п(ω), ²_20п(ω) – мощность, напряжение и ток помехи, наведенной на ближнем конце цепи, подверженной влиянию;

Ρ_2lп(ω), U_{2l п}(ω), ²_{2l п}(ω) – то же, на дальнем конце цепи, подверженной влиянию;

Ζ_В1(ω), Ζ_В2(ω), Ζ_l1(ω), γ₁(ω), Ζ_l2(ω), γ₂(ω) – Волновые сопротивления, коэффициенты распространения цепей, нагрузки на концах цепей соответственно.

Абсолютные значения мощностей и напряжений помех не дают представления о параметрах взаимных влияний линий связи, так как зависят от уровней сигналов во влияющей цепи, значения которых не связаны с параметрами цепи. Поэтому взаимные влияния между цепями принято характеризовать в относительных единицах отношением модулей кажущихся мощностей сигнала во влияющей цепи и помехи от взаимного влияния в цепи, подверженной влиянию, выраженным в логарифмическом масштабе. Подобные параметры влияний не зависят от абсолютных значений сигналов во влияющей цепи вследствие линейности рассматриваемой системы.

Определим основные параметры взаимного влияния между цепями линий связи.

Переходное затухание на частоте ω на ближнем конце линии, дБ или Нп,

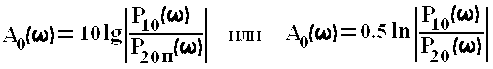
Переходное затухание на дальнем конце линии, дБ или Нп,

·

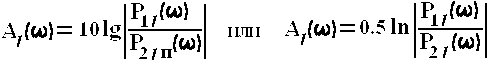1.3. Влияния в однородных симметричных линиях связи

Взаимные влияния между симметричными цепями обусловлены взаимодействием электромагнитных полей этих цепей, которое можно представить в виде суммарного воздействия электрического и магнитного полей. Влияние от электрического поля называют электрическим, а от магнитного поля магнитным. Значения электрического и магнитного влияний можно определить экспериментально и в некоторых случаях путем расчета.

Экспериментальные методы раздельного определения влияний основаны на измерении токов и напряжений во влияющей цепи и цепи, подверженной влиянию в режимах, когда между цепями существует в основном либо электрическое поле, либо магнитное. Эти условия создаются в коротких по сравнению с длиной волны сигнала λ=υ/f отрезках линий при режимах холостого хода (электрическое поле) и короткого замыкания (магнитное поле).

Отношение комплексных амплитуд тока помех I_2π(ω), наведенного в цепи длиной l, подверженной влиянию, и напряжения U₁(ω), во влияющей цепи, определенных в режиме холостого хода цепей, называют электрической связью между этими цепями, См:

(2)

где g₁₂ - активная составляющая электрической связи; iωk₁ - емкостная связь между цепями 1 и 2.

Магнитной связью между цепями 1 и 2 называют отношение комплексных амплитуд ЭДС, наведенной в цепи длиной l, подверженной влиянию Е_2π(ω), и тока I₁(ω) во влияющей цепи в режиме короткого замыкания в обеих цепях, Ом:

 

(3)

 

где r₁₂ - активная составляющая связи; m₁ - индуктивная составляющая связи между цепями 1 и 2.

Для однородных линий коэффициенты связи К₁₂(iω), См/км, и М₁₂(iω), Ом/км, обычно нормируют на единицу длины линии:

(4)

Под действием напряжения влияющей цепи U₁ в цепи, подверженной влиянию, возникает ток помехи, значение которого пропорционально разности частичных емкостей между проводами цепей 1 и 2 на длине линии l (с_{13 l} + с_{24 l}) - (с_{14 l} + с_{23 l}). Значение этой разности, отнесенное на единицу длины однородной линии, называют коэффициентом емкости или просто емкостной связью, Ф/км,

k₁= (с₁₃ + с₂₄ ) - (с₁₄ + с₂₃ ),

где с₁₃₌ с_{13 l} / l; с₂₄₌ с_{24 l} / l ; с₁₄₌ с_{14 l} / l; с₂₃₌ с_{23 l} / l .

Емкостная связь характеризует емкостную асимметрию между цепями, а после умножения на частоту сигналов определяет мнимую составляющую электрические связи.

Активная составляющая электрической связиg₁₂ между первой и второй цепями выражается через разность потерь в диэлектрике g_{13 l} , g_{14 l} , g_{24 l} аналогичным выражением, См/км

g_{12 =} (g₁₃₊ g₂₄ ) - (g_{14 +} g₂₃ ).

Индуктивная связь m₁ между цепями по аналогии представляется мостом частичных индуктивностей, имеющих трансформаторную связь. Коэффициент индуктивной связи характеризует асимметрию моста и соответственно относительную величину перехода энергии магнитного поля влияющей цепи в цепь, подверженную влиянию, Гн/ км,

 

m₁= ( m₁₃+ m₂₄)-( m₁₄+ m₂₃).

 

Активная составляющая магнитной связи r₁₂ обусловлена различием потерь на вихревые токи в проводах и металлических оболочках кабеля, возникающих вследствие несимметричности расположения проводов цепей относительно оболочки экранов и третьих цепей кабеля. В результате мост активных сопротивлений r_{13 l} , r_{23 l}, r_{14 l}, r_{24 l} расстраивается и появляется активная составляющая комплексной магнитной связи, Ом/км,

r₁₂ = (r₁₃ + r₂₄ ) - (r₁₄ + r₂₃).

1.4. Влияние между цепями симметричных кабельных линий связи

Общие положения.

Взаимные влияния между цепями симметричных кабельных линий связи характеризуются следующими особенностями:

• расстояния между цепями в симметричных кабельных линиях связи сопоставимы с диаметрами проводников кабеля, а окружающее цепи пространство заполнено диэлектриком, часто неоднородной структуры, проводниками соседних цепей, металлическими экранами и оболочками. Указанные факторы приводят к заметному искажению электромагнитных полей, возрастанию случайных составляющих электромагнитных связей и к усложнению задачи расчета и оценки взаимных помех;

• кабельные линии связи создаются в два этапа: на первом этапе изготавливаются строительные длины кабеля, на втором – строится кабельная магистраль;

• процессы индуцирования взаимных влияний в строительных длинах кабеля и на длинных линиях существенно различаются, что приводит к необходимости раздельного рассмотрения этих процессов. Кроме того, возникают задачи измерения и нормирования параметров влияния в строительных длинах кабеля и на ретрансляционных (усилительных и регенерационных) участках линии;

• симметричные кабельные линии используются для организации различных систем передачи (аналоговых и цифровых), работающих в диапазоне от тональных частот до десятков мегагерц. Это приводит к необходимости определения частотных характеристик первичных и вторичных параметров взаимных влияний для каждой из 10…12 систем передачи, работающих по симметричным кабелям.

• Рассмотрим параметры влияния в строительных длинах симметричных кабелей связи. В общем случае здесь необходимо учитывать все четыре первичных параметра влияния (m, k, r и g), причем в зависимости от частоты их соотношение и удельная значимость меняются.

В тональном спектре частот (0,3…3,4 кГц) значения активных составляющих электромагнитных связей (r и g) малы по сравнению с реактивными, а емкостная связь ωk₁Z_в на частоте 1 кГц примерно в 10 раз превышает магнитную (ωm₁/Z_в) вследствие большого значения Z_в (1 кГц) ≈ 600 Ом. Поэтому на строительной длине низкочастотных кабелей электромагнитные связи на ближний N_{12 нч} и дальний - F_{12 нч} концы кабеля оказываются примерно одинаковыми и равными N_{12 нч} ≈ F_{12 нч} ≈ iωk₁Z_в.

1.5. Влияния в строительных длинах кабеля

Теоретическое и экспериментальное исследование первичных параметров влияния в строительных длинах кабеля в области высоких частот сопряжено с большими трудностями в связи с невозможностью выполнения условия l_С.Д < λ_min/4, при котором | Z_x.x(ω) | >>| Z_в(ω) | θ | Z_кз(ω) | << | Z_в(ω) |, ΰ также со случайным характером электромагнитных связей. Так, строительная длина кабеля MKC-4×4×1,2 ñоставляет 0,825 км, а минимальная длина волны на частоте 252 кГц (система К-60) равна примерно 1 км, что делает невозможным раздельное измерение комплексных электрической и магнитной связей.

В качестве основного параметра взаимных влияний на строительных длинах кабеля приняты значения переходных затуханий на ближний и дальний концы цепей кабеля и их частотные характеристики.

Частотные характеристики переходных затуханий на ближнем А₀(ω)_С.Д и дальнем А_l(ω)_С.Д концах строительной длины зависит от значений и функции распределения электромагнитных связей по длине кабеля (параметр x) как между взаимовлияющими, так и между третьими физическими и искусственными цепями.

В области средних частот, при которых λ_min > (1,25…2,5)l_С.Д переходные затухания в строительных длинах кабеля определяются в основном непосредственными влияниями. Характеристики А₀(ω)_С.Д и А_l(ω)_С.Д имеют вид монотонно убывающих с ростом частоты кривых. Годографы ПФВП на ближнем конце А₀(iω)_С.Д обычно представляются начальными отрезками спирали. Кривые А_l(iω)_{С.Д 1/2} и А_l(iω)_{С.Д 2/1} имеют плавный характер, а различия влияния 1/2 и 2/1 незначительны по модулю и сравнительно малы по аргументу (фазе). Различия фазо-частотных характеристик А_l(iω)_{С.Д 1/2} и А_l(iω)_{С.Д 2/1} возрастают, если взаимовлияющие цепи расположены в разных четверках, когда фазовые постоянные цепей различаются друг от друга вследствие неодинаковых шагов скрутки четверки.

Косвенные влияния на строительных длинах кабеля в диапазоне частот до 250…500 кГц обычно остаются значительно меньше непосредственных влияний, что затрудняет их учет при измерении переходного затухания.

Вместе с тем уже в процессе изготовления магистральных симметричных кабелей возникает необходимость контроля косвенных влияний через третьи цепи и отражений, которые быстро возрастают при соединении строительных длин кабеля в процессе строительства кабельных магистралей. Поэтому в высокочастотных кабелях типа МКС и аналогичных им марок нормируются не только значения переходных затуханий на ближний и дальний концы строительной длины, но и значения емкостных связей между основными и искусственными цепями, расположенными в одной четверке (к₂ и к₃),емкостная асимметрия цепей относительно земли (e₁ и e₂), а также отклонения величины рабочей емкости.

Для иллюстрации приведем нормы на вышеуказанные величины для MKC-4×4×1,2, ïредназначенного для передачи сигналов до 252 кГц. В диапазоне частот до 12…252 кГц значения А₀(ω)_С.Д должны быть не менее 62,5 дБ для 90% комбинаций влияния и 59,0 дБ для 100% измеренных величин. Значения А_l(ω)_С.Д должны быть соответственно не менее 73,8 дБ для 90% и 67,7 дБ для 100% измеренных величин.

Распределение емкостных связей к₂, к₃ и емкостной асимметрии e₁ и e₂ – не более 230 пФ для 90% и 570 пФ для 100% измеренных величин. Отклонение рабочей емкости от номинального значения 25 нФ/км не должны превышать ±0,8 пФ/км.

Для контроля за косвенными влияниями во всем диапазоне рабочих частот производится измерение распределения так называемого параметра симметрируемости внутричетверочных комбинаций влияния, определяемого минимальным значением А_l(ω)_сим, которого можно достичь при компенсации непосредственных влияний. Для кабеля MKC-4×4×1,2 ýта величина должна составлять не менее 85,1 дБ для 90% и 80,8 дБ для 100% измеренных величин.

В области высоких частот (системы ЦСП и К-1020с), когда λ_min << l_{С. Д}, характер взаимных влияний между цепями на строительной длине кабеля изменяется. Усиливаются косвенные влияния между цепями, режимы работы основных и третьих цепей приближаются к режимам работы электрически длинных линий. Однако самое существенное изменение состоит в том, что структура параметров взаимных влияний на ближнем конце строительной длины кабеля при высоких частотах становится иной. Влияния уже не могут рассматриваться как единая случайная величина, а начинают распадаться на ряд случайных величин, соответствующих параметрам влияния более коротких отрезков кабеля. Этот процесс характеризуется множителем е^–(γ₁ ^{+ γ}₂^)l в уравнении (6.19) неравномерной зависимостью параметров влияния N₁₂ от х. Под воздействием этих факторов единые для строительных длин кабеля при низких и средних частотах параметры N₁₂(х, ω) распадаются на независимые случайные величины, число которых определяется значением радиуса частотной корреляции ρ(ƒ ) ÏФВП. При l_С.Д ≈ 1 км ρ(ƒ ) ≈ 0,5…1,2 ÌГц. Данное обстоятельство означает, что в интервале частот |ƒ₁ – ƒ₂ | = ∆ ƒ > ρ(ƒ ) βлияние на ближнем конце строительной длины кабеля при частоте ƒ₁ (ƒ₂). Указанный вывод следует из характера влияний, индуцируемых по закону ближнего конца. Возрастание фазовых сдвигов сигнала и помехи за счет множителя е^–(γ₁ ^{+ γ}₂^)l в уравнении (6.19) при неравномерном распределении связей по длине кабеля приводит к изменению величины и фазы составляющих помех, приходящих с отдельных участков строительной длины кабеля. В результате этого, а также вследствие все более заметного увеличения затухания токов помех, приходящих с дальних участков строительной длины кабеля с ростом частоты, изменяется исходная совокупность случайных величин, сумма которых при ∆ ƒ > ρ(ƒ) ρтановится практически независимой от исходного значения тока помех.

2. Кабельные линии связи

2.1. Классификация кабелей связи

Кабелем называется конструкция, состоящая из скрученных вместе изолированных проводников (сердечник), заключенных в общую влагозащитную оболочку и броневые покровы.

Кабели связи классифицируются по следующим признакам:

по области применения – на магистральную зоновые (внутриобластные, сельские, городские, для соединительных линий и вставок, а так же радиогоктотные кабели)

по условиям прокладки – на подземные, подводные, подвесные и кабели для протяжки в телефонной канализации;

по спектру передаваемых частот - на низкочастотные НЧ (тональные до 10кГц) и высокочастотные ВЧ (свыше 10кГц);

по конструкции – на симметричные и коаксиальные. Симметричная цепь состоит из двух совершенно одинаковых в конструктивном и электрическом отношении изолированных проводников (рис 1.1 а). Коаксиальная цепь представляет собой два цилиндра в совмещенной осью, причем один цилиндр – сплошной проводник, концентрически расположен внутри другого цилиндра - полого (рис 1.1б)

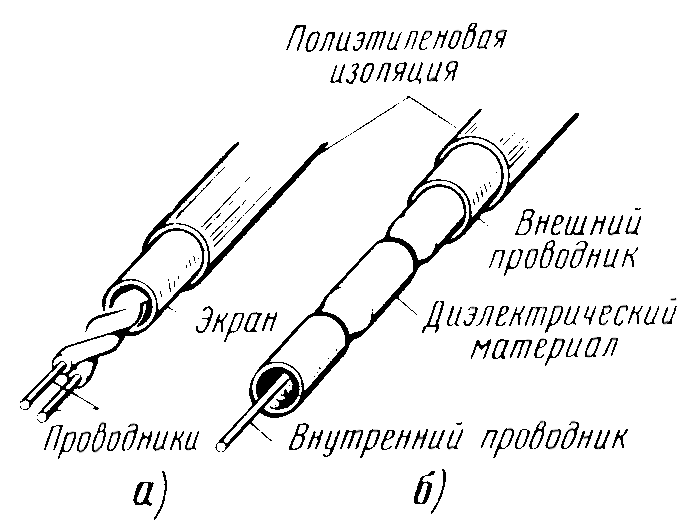
Рисунок 1.1.

Кроме того различают кабели:

 

по способу построения сердечника - с пучковой и повивной скруткой;

по способу скрутки жил – на парную и звездную скрутки;

по роду защитных оболочек – на кабели с металлическими, пластмассовыми и металлопластмассовыми оболочками;

по типу бронепокровов – на голые (безброневые) и бронированные стальными лентами либо плоскими или круглыми проволоками.

2.2. Конструктивные элементы кабелей связи

2.2.1. Токопроводящие жилы

Токопроводящие жилы кабелей связи должны обладать высокой электрической проводимостью, гибкостью и достаточной механической прочностью. Проволока, применяемая для кабельных жил. должна быть на всем протяжении гладкой. без трещин, спайки и иметь одинаковый диаметр. Токопроводящие жилы изготавливаются в основном из меди и алюминия.

Для кабелей городских телефонных сетей обычно используется медная проволока диаметром 0.32; 0.4; 0.5; 0.6; 0.7 мм, для междугородных кабелей диаметром 0.8; 0.9; 1.2; 1.4 мм. Наиболее широко применяются на городских сетях кабели с жилами диаметром 0.5 мм, для междугородной связи кабели с жилами диаметром 1.2 мм.

Алюминиевые жилы – используются в производстве кабелей связи, имеют диаметр 1.15; 1.55; 1.8 мм. Эти жилы аналогичны по электрической проводимости медным с диаметрами 0.9; 1.2; 1.4 мм соответственно. Применения алюминиевых жил вместо медных вызывает увеличение диаметра кабеля в 1.28 раза, а следовательно, и увеличение расхода дорогостоящего свинца на изготовление защитной оболочки. Поэтому применение алюминиевых жил наиболее рентабельно в кабелях без свинцовой оболочки.

Кабельные проводники имеют преимущественно сплошную цилиндрическую конструкцию. Кроме того используют проводники и более сложной конструкции. В тех кабелях, где требуется повышенная гибкость и механическая прочность, токопроводящая жила скручивается в литцу из нескольких проволок, чаще 7,12,19. Изготавливают кабели также с биметаллическими проводниками конструкции алюминий – медь, сталь – медь.

В подводных кабелях применяется многопроволочная жила, состоящая из проволок разного сечения. В центре такой жилы размещается толстый проводник, повив состоит из тонких проволок.

В коаксиальных кабелях внутренний проводник сплошной, а внешний представляет собой полый цилиндр, изготавливаемый из меди или алюминия.

В электрическом отношении наилучшей формой внешнего проводника коаксиального кабеля является однородная по всей длине трубка. Однако изготовить такой проводник крайне затруднительно. Промышленное применение нашли разновидности гибких внешних проводников коаксиального кабеля.

Наиболее широко в коаксиальных кабелях магистральной связи используется первая конструкция внешнего проводника (медный цилиндр со швом молния) как более технологичная и обеспечивающая требуемую электрическую однородность по длине.

2.2.2. Изоляция

В электрическом отношении свойства изоляции характеризуются следующими четырьмя параметрами:

• • электрической прочностью U, при которой происходит пробой изоляции;
  • удельным электрическим сопротивлением 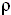, характеризующим величину тока утечки в диэлектрике;
  • диэлектрической проницаемостью 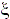, характеризующей степень смещения (поляризации) зарядов в диэлектрике при воздействии на него электрического поля;
  • тангенсом угла диэлектрических потерь tg 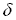(или величиной диэлектрических потерь), характеризующим потери высокочастотной энергии в диэлектрике.

Наилучшим диэлектриком является воздух, у которого 1, , tg 0.

Однако создать изоляцию только из воздуха практически невозможно.

Поэтому кабельная изоляция является комбинированной и содержит как воздух так и твердый диэлектрик, причем количество твердого диэлектрика должно быть минимальным и определяется требованиями устойчивости изоляции и жесткости ее конструкции. Изоляция должна предохранять токопроводящие жилы от соприкосновения между собой и строго фиксировать взаимное расположение жил в группе по всей длине кабеля.

Для изоляции жил кабелей наряду с бумагой применяются современные полимеры типа полиэтилен, стирофлекс (полистирол), фторопласт, поливинилхлорид и др.

Известны следующие типы изоляции кабелей связи:

Трубчатая, выполняется из бумажной или пластмассовой ленты, наложенной в виде трубки (рис 1.2а);

Кордельная, состоит из нити корделя, расположенного открытой спиралью на проводнике, и ленты, которая накладывается поверх корделя (рис 1.2б);

Сплошная, выполняется из сплошного слоя пластмассы (рис 1.2в);

Пористая, образуется из слоя пенопласта (рис 1.2г);

Баллонная, представляет собой тонкостенную пластмассовую трубку, внутри которой свободно располагается проводник. Трубка периодически в точках или по спирали обжимается и надежно удерживает жилу в цетре изоляции (рис 1.2д,е);

Шайбовая, выполняется в виде шайб толщиной 1.5–2.5 мм из твердого диэлектрика, насаживаемых на проводник через определенные промежутки 20-30 мм (рис 1.2ж);

Спиральная, представляет собой равномерно распределенную по длине проводника пластмассовую спираль, имеющую прямоугольное сечение (рис 1.2з);

Колпачковая, выполняется из цилиндрических, пластмассовых или керамических колпачков, насажанных на проводник вплотную (рис 1.2.1);

Втулочная, выполняется из полиэтиленовых втулок длиной 12мм, растяженных на проводнике с интервалом 6мм (рис 1.2.5и);

Ленточная, выполняется из продольно расположенной полиэтиленовой ленты толщиной 0,4мм, на которой имеется по четыре выступа высотой 1,2мм с интервалом 12мм;

Кордельно–трубчатая, состоит из полиэтиленового корделя диаметром 0,6 – 0,8 мм и полиэтиленовой трубки толщиной 0,2 – 0,3 мм.

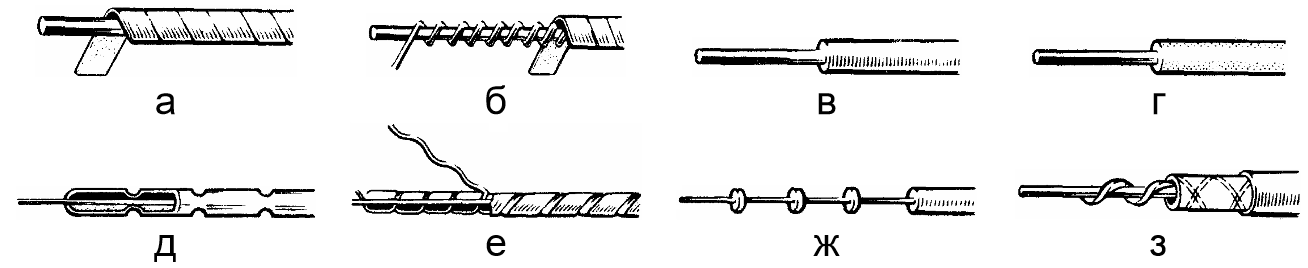
Рисунок 1.2.

Рисунок 1.2.1.

Наибольшее применение в настоящее время получили:

• для кабелей городской и сельской связи трубчатая, сплошная полиэтиленовая, пористая бумажная или полиэтиленовая;

• для симметричных кабелей междугородной связи кордельно – полистирольная, баллонная, кордельно–трубчатая или пористая из полиэтилена;

• для коаксиальных кабелей шайбовая, баллонная, спиральная и пористая. Во всех случаях диэлектриком является полиэтилен;

• для подводных коаксиальных кабелей сплошная полиэтиленовая изоляция.

2.2.3. Скрутка кабельных цепей

В симметричных кабелях применяется несколько способов скрутки изолированных проводников в группы (рис 1.3).

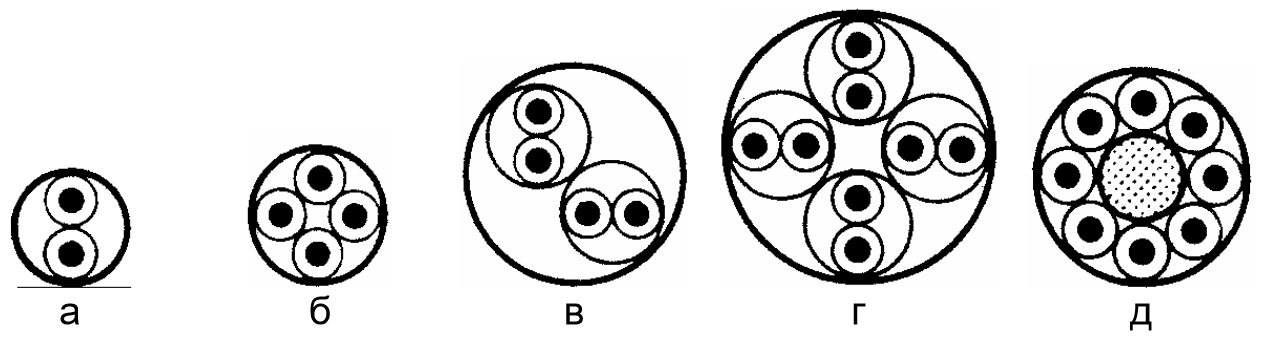
Рисунок 1.3

Парная скрутка (П) – две изолированных жилы скручиваются в пару с шагом скрутки не более 300мм (рис 1.3а).

Скрутка четверочная или звездная (3) - четыре изолированные жилы расположенные по углам квадрата, скручиваются с шагом скрутки 150 – 300 мм (рис 1.3б). разговорные пары (цепи) в этой скрутке образуются из диагональных жил. Так, жилы а и б образуют одну пару, а жилы с и д другую.

Скрутка двойная пара (ДП) – две предварительно свитые пары скручиваются между собой в четверку (рис 1.3в). Шаги скрутки пар должны быть отличными как один от другого так и от шага скрутки самой четверки. Шаг скрутки пар принимается в пределах 400 – 800 мм, а шаг скрутки четверки 150 – 300 мм.

Скрутка двойной звездой (ДЗ) – четыре предварительно свитые пары вновь скручивают вместе по способу звезды, образуя восьмерку (рис 1.3г). Шаги скрутки пар, составляющих восьмерку, делают различными и берут в пределах 150 – 250 мм, а шаг скрутки восьмерки 200 – 400 мм. Направление скрутки пар и скрутки восьмерки должны быть противоположными.

Восьмерочная скрутка (В) – восемь жил группы располагаются концентрически вокруг сердечника из изолированного материала, например стирофлексного полиэтиленового корделя (рис 1.3д).

Наиболее экономичной,обеспечивающей лучшую стабильность по электрическим параметрам, является звездная скрутка. Эта скрутка получила преимущественное применение в междугородных кабелях связи.

Группы (пары, четверки и т.д.) скручиваются в общий кабельный сердечник. Различают две системы скрутки в сердечник: пучковую и повивную. При пучковой скрутке группы сначала скручиваются в пучки (по 50 или 100 групп), после чего пучки скручиваются в сердечник.

При повивной скрутке группы располагаются последовательными концентрическими слоями (повивами) вокруг центрального повива, состоящего из одной – пяти групп.

При повивной скрутке число групп в каждом последующем повиве n_x увеличивается на шесть по сравнению с предыдущим n:

n_x =n+6

Исключением из этого правила является второй повив в том случае, когда в первом (центральном) повиве имеется лишь одна группа. Тогда во втором повиве увеличение будет не на шесть, а на пять групп.

2.2.4. Защитные оболочки и покровы

Сердечник кабеля, состоящий из скрученных по определенной системе групп, покрывают поясной изоляцией и заключают в герметичную оболочку, предохраняющую кабель от влаги и возможных механических воздействий, которые могут возникнуть в процессе транспортировки, прокладки и эксплуатации кабеля.

В кабельной промышленности применяют следующие кабельные оболочки: металлические, пластмассовые и металлопластмассовые.

К металлическим оболочкам относятся, главным образом, свинцовые, алюминиевые и стальные. Свинцовые оболочки накладывают на кабель методом опрессования в горячем виде. Чтобы свинцовая оболочка имела большую твердость и вибростойкость, ее изготовляют из легированного свинца с присадкой 0,4 – 0,8 % сурьмы. Толщина свинцовых оболочек в зависимости от диаметра кабеля приведена в табл. 2.12.

Таблица 2.12

Алюминиевые оболочки выпрессовывают в горячем виде или изготовляют холодным способом из ленты со сварным продольным швом. Известны методы сварки оболочки из алюминиевых лент высокочастотными токами или способом холодной сварки, давлением. Для больших диаметров кабеля (свыше 20–30 мм применяют алюминиевые) оболочки гофрированной конструкции.

Применение алюминиевых оболочек является весьма прогрессивным. Алюминиевая оболочка легкая, дешевая и обладает высокими экранирующими свойствами. Однако алюминий весьма подвержен электрохимической коррозии и поэтому его надежно защищают полиэтиленовым шлангом.

Стальные оболочки изготовляют путем сварки лент толщиной 0,3–0,5 мм, свернутых в трубку. Для повышения гибкости стальные оболочки подвергают гофрированию. С целью защиты от коррозии стальные оболочки покрывают полиэтиленовым шлангом с предварительно наложенным слоем битума. Стоимость стальных оболочек составляет 50% от стоимости свинцовой оболочки и 64 % от алюминиевой . Такие оболочки не требуют дополнительной механической защиты.

Из пластмассовых оболочек наибольшее использование получили полиэтилен, поливинилхлорид и полизобутиленовые композиции. Пластмассовые оболочки выгодно сочетают влагостойкость, стойкость против электрической и химической коррозий и придают кабелю легкость, гибкость и вибростойкость. Однако через пластмассу постепенно диффундируют водные пары, что приводит к падению сопротивления изоляции кабеля. Поэтому пластмассовые оболочки применяют, главным образом, в кабелях с негигроскопической изоляцией типа полиэтилена, фторопласта и др.

В настоящее время известна целая серия комбинированных металлопластмассовых оболочек. Оболочка "алпэт" состоит из продольно-наложенной (с перекрытием) на сердечник кабеля гофрированной алюминиевой ленты толщиной 0,2 мм и полиэтиленового шланга. Оболочка "сталпэт" состоит из двух гофрированных лент – алюминиевой толщиной 0,13–0,2 мм и стальной оцинкованной толщиной 0,2 мм, - наложенных на сердечник продольно, и наружного полиэтиленового шланга. При этом нижнюю – алюминиевую – ленту накладывают с небольшим зазором, а верхнюю – стальную – с перекрытием. Продольный шов стальной ленты сваривают.

Известны также комбинированные оболочки, в которых сочетаются тонкая оболочка из свинца и полиэтиленовый шланг (оболочка "свипэт"). Такие оболочки используются для защиты кабелей от повреждений при ударах молнии, а также для защиты свинца от коррозии.

Сопоставляя различные конструкции защитных оболочек, следует отметить как наиболее перспективные алюминиевые и стальные, надежно защищенные полиэтиленовым шлангом.

Снаружи кабеля располагаются бронепокровы, защищающие кабель от механических повреждений и коррозии. В состав этих покровов входят три основные части: стальной покров и два волокнистых покрова, располагаемых под и над броней.

Волокнистые покровы состоят из кабельной пряжи (джута), пропитанной битумным составом.

В зависимости от механических воздействий на кабель в процессе прокладки и эксплуатации применяются следующие разновидности брони

• две стальные ленты (марка Б);

• повив из круглых стальных проволок (марка К);

• повив из плоских стальных проволок (марка П);

Кроме того, применяется усиленная двойная броня, состоящая из комбинации различных типов брони (БК, КК).

2.3. Маркировка кабелей связи

Для удобства классификации и пользования кабелями им присваивается определенное условное обозначение – марка кабеля. Магистральные и междугородные кабели маркируются буквой М; буквы КМ обозначают коаксиальные магистральные. Телефонным городским кабелям присваивается буква Т. Если кабель имеет стирофлексную (полистирольную) изоляцию, то дополнительно вводится буква С, полиэтиленовую изоляцию – то буква П. В кабелях с алюминиевой оболочкой еще добавляется буква А, а со стальной – буква С.

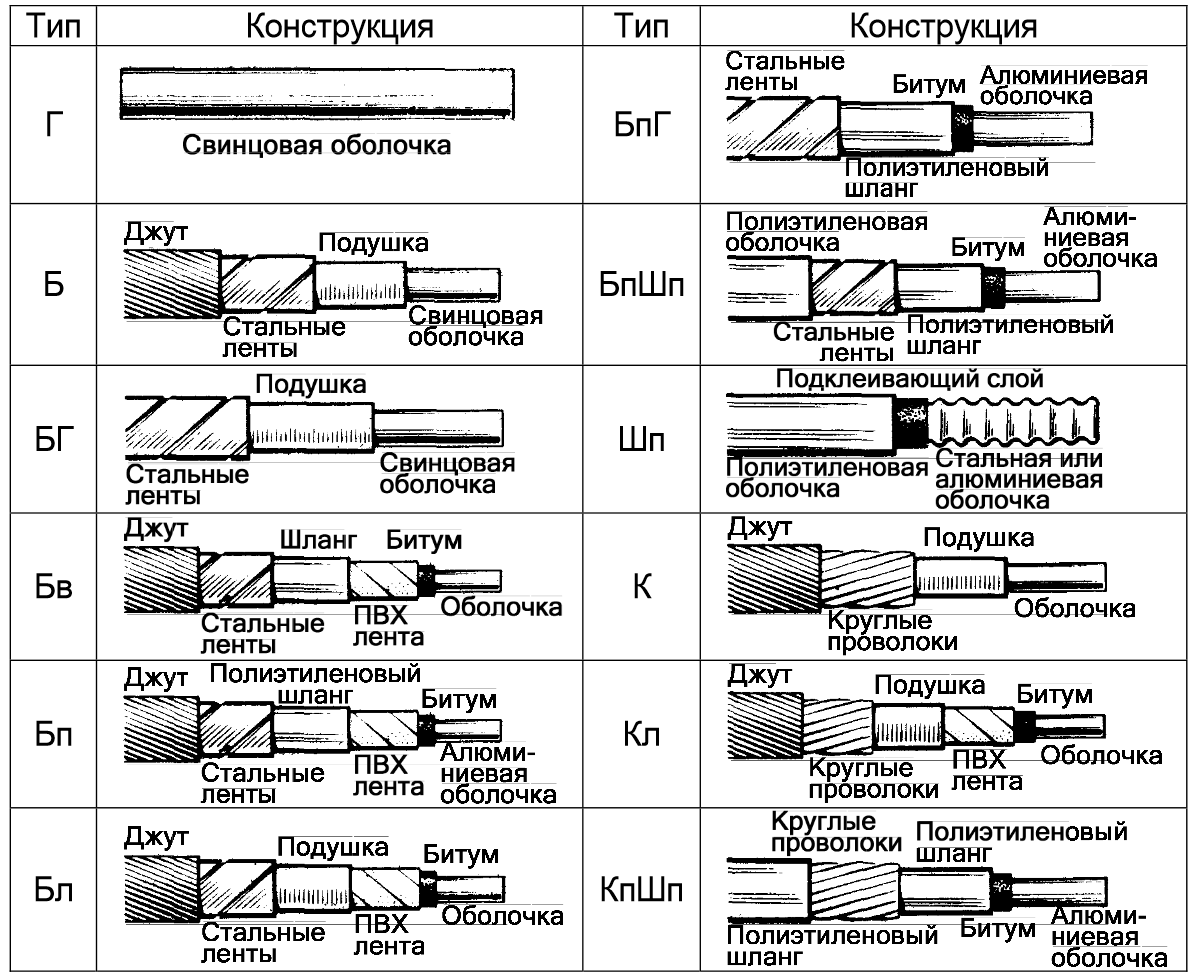
В зависимости от вида защитных покровов кабели маркируются буквами: Г – голые (освинцованные), Б – с ленточной броней и К – с кругло проволочной броней. Наличие наружной пластмассовой оболочки обозначается буквой П (полиэтиленовая) или В (поливинилхлоридная).

2.3.1. Междугородные коаксиальные кабели

Магистральный коаксиальный кабель 2,6/9,4 марки КМБ-4 состоит из четырех коаксиальных пар и пяти звездных четверок (рис 1.4.). Каждая коаксиальная пара состоит из внутреннего медного проводника диаметром 2,6 мм и внешнего проводника в виде медной трубки диаметром 9,4 мм с одним продольным швом. Коаксиальная пара имеет изоляцию из полиэтиленовых шайб толщиной 2,2 мм с расстоянием между ними 25 мм. Поверх внешнего проводника расположен дополнительный экран в виде двух мягких стальных лент толщиной 0,15 – 0,2 мм, который покрывается одним – двумя слоями кабельной бумаги. Кабель имеет свинцовую оболочку и обычные броневые покровы и маркируется КМБ, КМГ и КМК. Кабель типа 2,6/9,4 используется в основном по однокабельной системе.

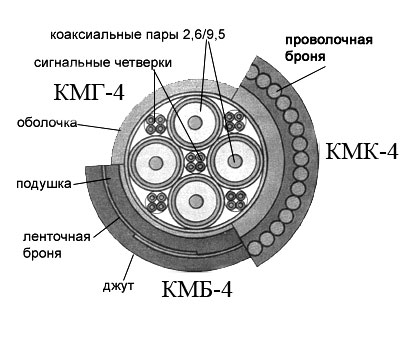
Рисунок 1.4

В четырехкоаксиальном кабеле две диаметрально расположенные коаксиальные пары служат для многоканальной телефонной связи, а вторые две пары - для телевидения. По телефонным парам можно передавать 1920 каналов в спектре 312 8500 кГц. Для телевидения как черно – белого, так и цветного занимается спектр частот 6 МГц.

Возможно также использование коаксиальной пары для 300 телефонных разговоров в спектре 312 1500 кГц и телевизионных программ в спектре 1900 8500 кГц.

Имеются системы уплотнения кабеля в спектре до 12 МГц, по которым можно получить 2700 телефонных каналов, и до 17 МГц для 3600 каналов.

Малогабаритные коаксиальные кабели изготовляются с диаметрами:

1,2/4,6; 1,2/5,3; 1,5/5,4 и др. Наибольшее применение получил кабель с соотношением диаметров проводников 1,2/4,6 мм.

Малогабаритные коаксиальные кабели предназначены для строительства кабельных магистралей ограниченной протяженности, рокадных линий между магистралями, устройство глубоких вводов радиорелейных линий и обеспечения областных связей.

Достоинством малогабаритных кабелей является простота конструкции, дешевизна и технологичность их изготовления. Если средние коаксиальные кабели целесообразно применять при большом пучке связей (500 и больше), то малогабаритные кабели эффективны и при малом числе каналов, начиная с десятков (60-120). Эти кабели, вотличие от симметричных, не требуют выполнения сложных работ по симметрированию.

Наибольшее применение получил четырехкоаксиальный малогабаритный кабель. Он может изготавливаться как в пластмассовой оболочке (МКТП- 4), так и в свинцовой оболочке с ленточной броней (МКТСБ–4). Сердечник кабеля в обоих случаях идентичный.

Комбинированные коаксиальные кабели содержат средние пары 2,6 9,4, малогабаритные коаксиальные пары 1,2 4,6 и симметричные группы. Комбинированные кабели позволяют:

• • организовать мощные пучки телефонных каналов и телевизионную передачу на большие расстояния по коаксиальным парам 2,6/9,4 при помощи систем уплотнения К-1920 и К-3600;
  • обеспечить распределительные каналы по связи между городами и промежуточными пунктами, расположенными по магистрали по коаксиальным парам 1,2/4,6 при помощи системы К – 300 и в последующем системы К – 1320 ;
  • обеспечить выделение необходимого количества каналов в любом пункте трассы из системы уплотнения аппаратуры К -300 и системы К - 24к уплотнения симметричных пар ;
  • организовать служебную связь и телесигнализацию по симметричным парам и четверкам.

2.3.2. Междугородные симметричные кабели

Междугородные симметричные кабели подразделяются на три вида: кабели с кордельно–бумажной изоляцией МК, с кордельно-полистирольной (стирофлексной) изоляцией МКС и с полиэтиленовой изоляцией МКП. Наружные оболочки изготавливаются из свинца, алюминия или стали.

Для междугородной связи применяются в основном кабели конструкции 4*4 и 7*4, а для зоновой (внутриобластной ) связи – 1*4.

Кабели предназначены для высокочастотного уплотнения в спектре до 252 кГц, аппаратурой К–60, работающей при напряжении дистанционного питания 1000 В постоянного тока (690 В переменного тока). Расстояние между НУП – 20 км, между ОПУ – 160 –250 км. Максимальная дальность – 12500 км.

Наибольшее применение имеют кабели с кордельно-полистирольной (стирофлексной) изоляцией МКС. В зависимости от типа оболочки они классифицируются: МКС – в свинцовой оболочке, МКСА – в алюминиевой оболочке, МКСС – в стальной оболочке. Во всех случаях сердечник кабеля идентичен. Кабели типа МКС изготавливаются в виде конструкций 7*4 ; 4*4 и 1*4 строительной длиной 825 м.

Конструкция наиболее распространенного четырехчетверочного симметричного кабеля с кордельно–полистирольной изоляцией МКС – 4*4 приведена на рис 1.5. Диаметр медных жил – 1,2 мм. Токопроводящие жилы высокочастотных четверок изолируются разноцветным полистирольным корделем диаметром 0,8 мм и полистирольной лентой толщиной 0,05 мм с перекрытием 25 30%. Первая пара каждой четверки состоит из красного и желтого цветов, вторая пара – из жил синего и зеленого цветов.

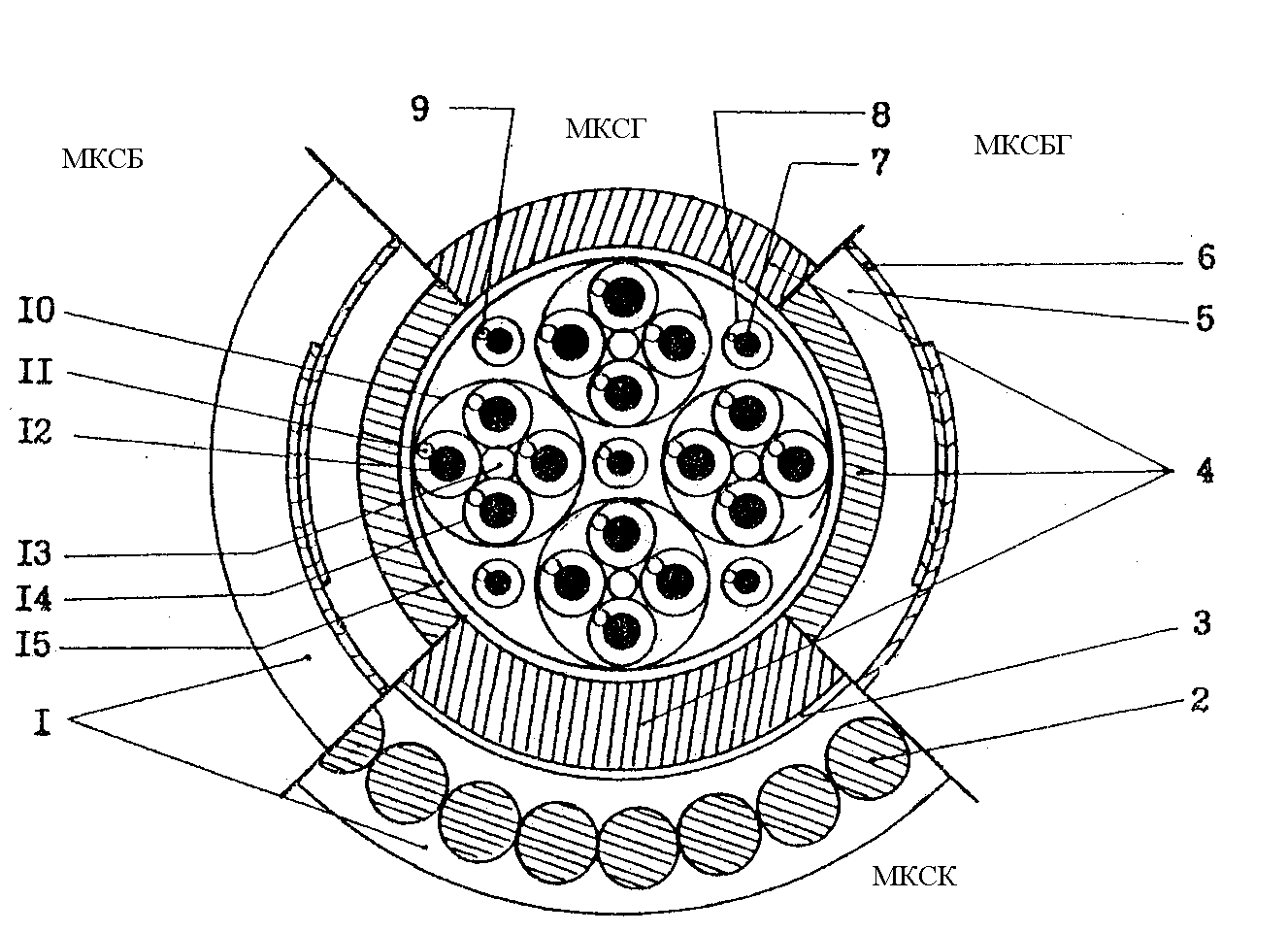
Рисунок 1.5

1 - Наружный покров (джут)

2 - Бронепроволока

3 - Две ленты крепированной бумаги

4 - Свинцовая оболочка

5 - Подушка

6 - Две бронеленты

7 - Медная проволока диаметром 0.9мм

8 - Полистирольная лента

9 - Кордель диаметром 0.4 мм

10 - Цветная хб пряжа

11 - Кордель диаметром 0.8 мм

12 - Токопровоящая жила диаметром 1.2мм

13 - Центрирующий кордель диаметром 1.1мм

14 - Полистирольная лента

15 - Поясная изоляция

Две жилы в четверке, расположенные по диагонали, образуют рабочую пару. Изоляция жил первой пары четверки имеет красный и желтые цвета, второй пары – синий и зеленый. Внешне четверки отличаются расцветкой хб пряжи или ленты из синтетического материала, наложенной поверх четверки открытой спиралью. Цвет соответственно порядковым номерам следующий: первая (счетная) - красный; вторая (направления счета) – зеленый, третья – синий; четвертая – желтый.

Центр четверки заполняется стирофлексным корделем диаметром 1,1 мм. Шаги скрутки всех четверок различны, взаимно согласованы и лежат в пределах 125 275 мм.

Кабели со свинцовой оболочкой и соответствующей броней имеют марки: МКСГ, МКСБ и МКСК. Толщина свинцовой оболочки у кабеля МКСБ – 1,25 мм а у остальных 1,4мм.

Кабели с алюминиевой оболочкой имеют поверх алюминия антикоррозийный защитный покров в виде битума и полиэтиленового шланга. В названии таких кабелей дополнительно приписываются буквы "АП": МКСАП, МКСАПБ, МКСАПК и др. Толщина алюминиевой оболочки при высокочастотной сварке – 1.0 мм, при прессовании – 1,3 мм.

Кабели в стальной оболочке маркируются МКССП. Стальная оболочка имеет толщину 0,4 мм и для большей гибкости гофрируется по всей длине. Поверх стали наносится антикоррозийный покров ввиде битума и полиэтиленового шланга.

2.3.3. Зоновые (внутриобластные) кабели

Для зоновой связи, т.е. связи областного центра с районами, нашли применение однокоаксиальные кабели ВКПАП–1 (с парой 2,1/9,7), уплотняемые аппаратурой К–120 по однокабельной системе, и одночетверочные кабели различных модификаций с полиэтиленовой МКП – 1*4 и кордельно–полистирольной (стирофлексной) МКС – 1*4 изоляцией, уплотняемые аппаратурой К-60 по двухкабельной системе.

3. Коаксиальные кабели

3.1. Электрические процессы в коаксиальных цепях

Способность коаксиальной цепи (пары) пропускать широкий спектр частот конструктивно обеспечивается коаксиальным расположением внутреннего и внешнего проводников. Особенности распространения электромагнитной энергии по коаксиальной паре обусловливают возможность передачи широкого спектра частот и ставят высокочастотные связи в преимущественное положение по сравнению с низкочастотными. Как будет показано ниже, взаимодействие электромагнитных полей внутреннего и внешнего проводников коаксиальной пары таково, что внешнее поле равно нулю. Рассмотрим раздельно электрическое и магнитное поле коаксиальной пары.

Результирующее магнитное поле коаксиальной пары представлено на рисунке 1.1, где показаны также напряженности магнитного поля H_φ^а и H_φ^б каждого проводника (а и б) в отдельности. В металлической толще проводника а магнитное поле Н_φ^а= I/2πr, где r – расстояние от центра проводника. Поле Н_φ^бпроводника б вне его выражается таким же уравнением, как и для сплошного проводника: Н_φ^б=I/2πr, где r – расстояние от центра полого проводника. Поэтому при определении внешних магнитных полей коаксиального кабеля параметр r для проводников а и б принимается одинаковым и исчисляется от центра проводников (нулевой точки).

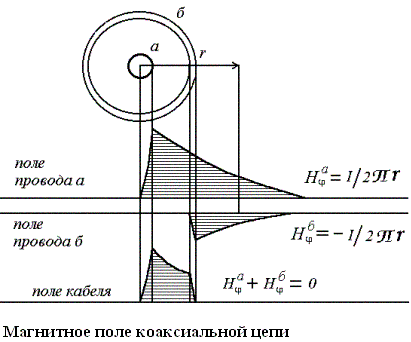
Рис 1.1

Учитывая, что точки в проводниках а и б равны по величине и обратны по знаку, магнитные поля внутреннего и внешнего проводников H_φ^а и H_φ^б в любой точке пространства вне коаксиальной пары также будут равны по величине и направлены в разные стороны. Следовательно, результирующее магнитное поле вне коаксиальной пары равно нулю:

H_φ = H_φ^а + H_φ^б= (I/2πr) + (-I/2πr) = 0.

Таким образом, силовые линии магнитного поля располагаются внутри коаксиальной пары в виде концентрических окружностей; вне коаксиальной пары магнитное поле отсутствует. Электрическое поле внутри коаксиальной пары также замыкается по радиальным направлениям между проводниками а и б ,а за ее пределами равно нулю.

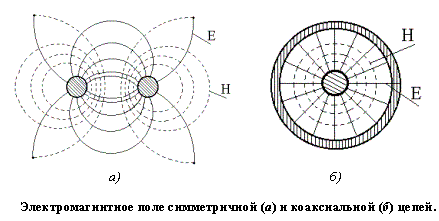
Рис 1.2

На рис.1.2 изображены электромагнитные поля коаксиальной и симметричной цепи. Как видно из рисунка, электромагнитное поле коаксиальной пары полностью замыкается внутри нее, а силовые линии электрического поля симметричной пары действуют на довольно значительном от нее расстоянии. Отсутствие внешнего электромагнитного поля обусловливает основные достоинства коаксиальных кабелей: широкий диапазон частот, большое число каналов, защищенность от помех и возможность организации однокабельной связи. В симметричных цепях из-за наличия внешнего электромагнитного поля возникают вихревые токи в соседних цепях и окружающих металлических массах (свинцовой или алюминиевой оболочке, экране и т.д.) и часть энергии рассеивается в виде потерь на тепло.

3.2. Первичные параметры коаксиальной цепи

В отличие от проводников, где имеются свободные электроны и действует ток проводимости І_пр, в диэлектрике нет свободных электронов, а имеются ионы и связанные диполи. Под действием переменного электромагнитного поля в диэлектрике происходит смещение диполей, их переориентация и поляризация.

Поляризацией называется смещение положительных и отрицательных зарядов в диэлектрике под действием электрического поля. Переменная поляризация обусловливает возникновение и действие токов смещения – емкостных токов І_см и вызывает затраты энергии на переориентацию диполей (потери в диэлектрике). Чем выше частота колебаний, тем сильнее токи смещения и больше потери. При постоянном токе эти явления отсутствуют.

Явления в диэлектрике полностью характеризуются двумя параметрами: емкостью С, определяющей способность поляризации и величину токов смещения, и проводимостью G, определяющей величину потерь в диэлектрике. Емкость кабеля аналогична емкости конденсатора, где роль обкладок выполняют проводники, а диэлектриком служит расположенный между ними изоляционный материал или воздух. При определении емкости коаксиального кабеля учитывают, что он аналогичен цилиндрическому конденсатору и его электрическое поле создается двумя цилиндрическими поверхностями с общей осью. Вследствие осевой симметрии напряженность электрического поля имеет равные потенциалы на определенном расстоянии от центра кабеля.

Проводимость изоляции G может быть определена как составляющая потерь в диэлектрике конденсатора, емкость которого эквивалентна емкости кабеля (рис. 2.1).

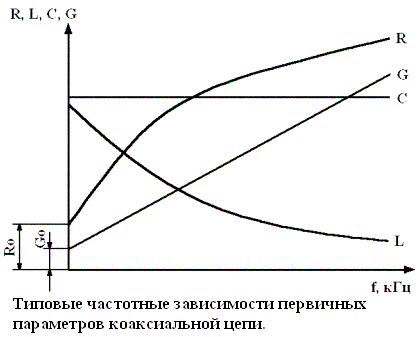
Рис 2.1

Проводимость изоляции и емкость коаксиального кабеля могут быть рассчитаны по формулам. Емкость C=2πε_a/ln(r_b/r_a), Ф/м. Проводимость изоляции G=2πσ/ln(r_b/r_a), См/м.

Обычно принято проводимость изоляции G выражать через тангенс угла диэлектрических потерь в изоляции кабеля

tg δ=G/ωC=σ/ωε_a.

Тогда G = [2π/ln(r_b/r_a)] ωε_a tg δ = ωC tg δ.

Заменяя в выражении емкости ε_а=ε₀ε_r , получим для 1 км кабеля (где ε₀=10^-9/(36π), Ф/м)

C=ε_r10^-6/[18ln(r_b/r_a)].

Соответственно

G=ωC tg δ, Cм/км,

Тип кабеля	Тип изоляции	εэ	Отношение υд/υв	tg δэ 10-4 при частоте, МГц
				1	5	10	60
2,6/9,5	Полиэтиленовая шайба	1,13	8,8	0,5	0,5	0,7	0,8
2,6/9,5	Полиэтиленовая спираль	1,1	6	0,4	0,4	0,5	0,6
1,2/4,6	Баллонно-полиэтиленовая	1,22	9	1,2	1,3	1,5	―
2,1/9,7	Пористо-полиэтиленовая	1,5	50	2	3	3	―
5/18	Кордельно-стирофлексная	1,19	12	0,7	0,8	1,0	1,2

где ε_r и tg δ – δиэлектрическая проницаемость и тангенс угла диэлектрических потерь изоляции. Эффективность значения ε_э и tg δ_э комбинированной изоляции, применяемой в коаксиальных кабелях, приведены в таблице.

В общем виде, кроме проводимости изоляции, обусловленной диэлектрическими потерями G, необходимо учитывать также проводимость, обусловленную утечкой тока в силу несовершенства изоляции: G=1/R_из. По величине эта проводимость изоляции обратно пропорциональна сопротивлению изоляции кабеля. В коаксиальных кабелях R_из нормируется величиной 10 000 МОм·км. Таким образом, проводимость изоляции коаксиального кабеля, G=1/R_из+ωC·tgδ, См/км. По абсолютной величине в используемом диапазоне частот второй член существенно больше первого, поэтому 1/R_из можно не учитывать.

Проанализируем полученные результаты и рассмотрим зависимости первичных параметров коаксиального кабеля. На рис.2.1 приведены частотные зависимости параметров коаксиального кабеля

Из рисунка видно, что с тостом частоты активное сопротивление закономерно возрастает за счет поверхностного эффекта и эффекта близости. Причем наибольшее удельное значение имеет сопротивление внутреннего проводника: величина R_а больше R_б в 3-4 раза. Индуктивность с увеличением частоты уменьшается. Это обусловлено уменьшением внутренней индуктивности проводников L_а и L_б за счет поверхностного эффекта. Внешняя индуктивность L_вш не меняется с изменением частоты. Емкость не зависит от частоты. Проводимость изоляции с ростом частоты линейно возрастает. Величина ее зависит в первую очередь от качества диэлектрика, используемого в кабеле и характеризуемого величиной угла диэлектрических потерь tg δ.

3.3. Вторичные параметры передачи коаксиальной цепи

Коаксиальные кабели практически используются в спектре частот от 60 кГц и выше, где R<<ωL и G<<ωC. Поэтому вторичные параметры передачи их рассчитываются по следующим формулам:

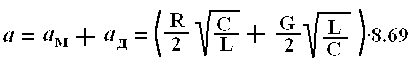
где а_м – коэффициент затухания вследствие потерь в металле; а_д – коэффициент затухания вследствие потерь в диэлектрике.

Однако вторичные параметры передачи коаксиальных кабелей целесообразно выражать непосредственно через габаритные размеры (d и D) и параметры изоляции(ε и tg δ).

Коэффициент затухания а, дБ/км, находится при подстановке в формулу первичных параметров. Для кабеля с медными проводниками получим:

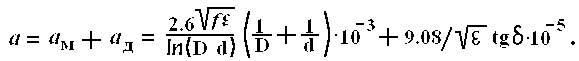
При замене медных проводников на алюминиевые затухание возрастает пропорционально соотношению активных сопротивлений или соответствий обратно пропорционально корню квадратному или проводимостей металлов

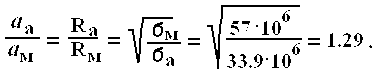
т.е. затухание коаксиального кабеля с алюминиевыми проводниками больше, чем с медными, на 29%.

При замене только внешнего проводника на алюминиевый затухание возрастает в соотношении

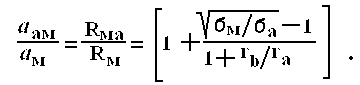
При соотношении радиусов проводников r_b/r_a=3.6 получим

а_ма/а_м=R_ма/R_м=1.06,

т. е. Затухание кабеля возрастает всего на 6%.

Изложенное дает основание сделать вывод о целесообразности применения коаксиальных кабелей с внешним алюминиевым проводником. В этом случае затухание увеличивается всего на 6%, а расход меди на изготовление коаксиального кабеля сокращается на 65%.

Потери в металле а_и изменяются пропорционально , а потери в диэлектрике а_д связаны с частотой линейным законом и с увеличением ƒ

Возрастают значительно быстрее (Рис.3.1).

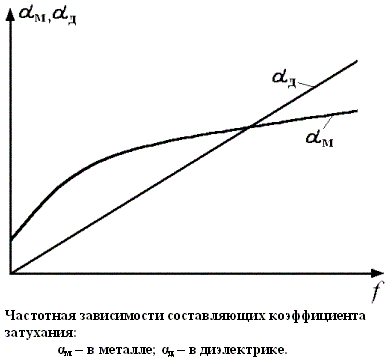
Рис 3.1

При использовании высококачественных диэлектриков (с малым tg δ) можно добиться в определенном частотном диапазоне очень малых диэлектрических потерь и положить а_д=0. при очень высоких частотах они настолько возрастут, что величина а_д играет значительную роль в общем затухании кабеля. В практически используемом спектре частот передачи по коаксиальным кабелям (до 60·10⁶ Гц) при современных кабельных диэлектриках величина а_д незначительна (не превышает 2-3% а_м) и затухание увеличивается примерно пропорционально .

Коэффициент фазы β, рад/км, коаксиальной пары определяется из уравнения . Подставляя сюда значения L и C, получим . Коэффициент фазы можно выразить также через С и , рад/км, где С – скорость света равная 300 000 км/с.

Скорость распространения υ, км/с, электромагнитной энергии по коаксиальным парам

.

Коэффициент сдвига фаз определяет длину волны в кабеле:

Из приведенных формул видно, что коэффициент фазы возрастает с увеличением частоты прямолинейно. Это обусловливает почти полное постоянство скорости передачи энергии по коаксиальному кабелю во всем рассматриваемом спектре частот. Скорость передачи уменьшается с увеличением диэлектрической проницаемости. Так, при сплошной полиэтиленовой изоляции (ε_r=2.3) с=200 000 км/с, а при воздушно комбинированной изоляции коаксиальной пары (ε_r=1.1), с=285 000 км/с.

Скорость передачи энергии по коаксиальным парам выше, чем по симметричным, и почти приближается к скорости распространения электромагнитных волн в воздухе (300 000 км/с).

Волновое сопротивление Ζ_в, Ом, коаксиальной пары для высоких частот определяется выражением

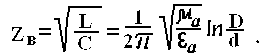
или

где - волновое сопротивление диэлектрика.

Имея в виду, что μ_а=μ₀μ_r и α_a=ε₀ε_r ,где μ₀=4π·10^-7, Гн/м, и ε₀=10^-9/36π, Τ/м, получим

где - волновое сопротивление воздушного пространства. Для среды μ_r=1 получим

В коаксиальных парах со сплошным диэлектриком (ε_r=2.3) Ζ_B=50 Ом, а при комбинированной изоляции (ε_r=1.1) величина волнового сопротивления составляет примерно 75 Ом.

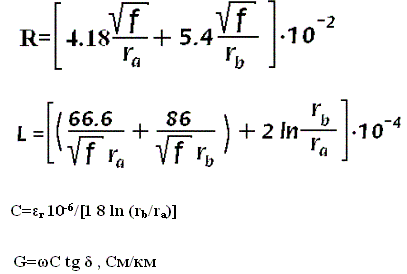
Формулы

4. Симметричные кабели

4.1. Электрические процессы в симметричных цепях

Электромагнитное поле симметричной цепи показано на рисунке. В отличие от коаксиального кабеля, не имеющего внешнего поля, в симметричной цепи поле открытое, действующее на значительном расстоянии.

Под действием переменного поля происходит перераспределение электромагнитной энергии по сечению проводников, при этом наблюдаться следующие явления: поверхностный эффект; эффект близости соседних проводников; воздействие на параметры цепи окружающих металлических масс(соседних проводников, экрана брони). В симметричных кабельных цепях действуют все три фактора одновременно. В воздушных линиях, где провода расположены сравнительно далеко друг от друга и отсутствуют наружные металлические оболочки, следует учитывать лишь поверхностный эффект. В коаксиальных кабелях, являющихся закрытой системой, не учитывается действие окружающих металлических масс.

За счет указанных явлений происходит перераспределение электромагнитного поля и изменяются параметры цепей. Активное сопротивление R и емкость С возрастают, индуктивность L уменьшается. Наиболее существенно возрастет сопротивление цепи:

R = R₀ + R_п.э + R_э.б + R_м ,

где R₀ - сопротивление постоянному току; R_п.э - сопротивление за счет эффекта близости; R_м- сопротивление, обусловленное потерями в окружающих металлических массах.

Поверхностный эффект был рассмотрен ранее.

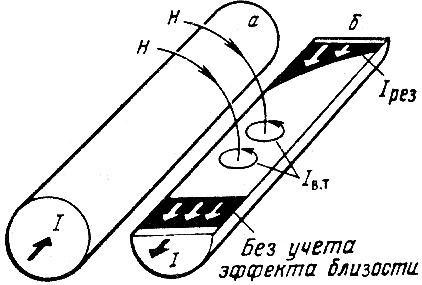
Эффект близости связан с взаимодействием внешних полей. Как видно из рис. 1, внешнее поле Н проводника а, пересекая толщу проводника б, наводит в нем вихревые тока. На поверхности проводника б, обращенной к проводнику а, они совпадают по направлению с протекающим по нему основным током (I+I_в.т), на противоположной поверхности проводника б, они направлены навстречу основному току (I- I_в.т). Аналогичное перераспределение токов происходит в проводнике а.

При взаимодействии вихревых токов с основным плотность результирующего тока на обращенных друг к другу поверхностях проводников а и б увеличиваться, а на отдаленных - уменьшается. Это явление ("сближение" токов в проводниках а и б) носит название эффект близости. Из-за неравномерного тока увеличивается активное сопротивление цепи переменному току.

Эффект близости также прямо пропорционален частоте, магнитной проницаемости, проводимости и диаметру проводника и, кроме того, зависит от расстояния между проводниками. С уменьшением этого расстояния действие эффекта близости возрастает в квадрате. Если по двум соседним проводникам токи проходят в одном направлении, то перераспределение их плотности из-за взаимодействия внешних электромагнитных полей приводит к увеличению плотности токов на взаимно отдаленных поверхностях проводников а и б.

4.2. Емкость и проводимость изоляции симметричной цепи

Емкость С и проводимость изоляции G связаны с процессами в диэлектрике. Под действием переменного электромагнитного поля в диэлектрике происходит смещение диполей, их переориентация и поляризация. Емкость характеризует способность поляризации и величину токов смещения, проводимость изоляции определяет величину потерь в диэлектрике на переориентацию диполей и характеризуется тангенсом угла потерь tgδ.

Емкость и проводимость изоляции симметричных цепей можно рассчитать по ранее выведенным формулам. Обычно принято проводимость изоляции выражать через тангенс угла диэлектрических потерь: tgδ=G/(ωC)=σ/(σε_a). При этом G= ωπε_atgδ/ln[(a-r/r)]=ωC tgδ. Заменяя в данном выражении ε_a=ε_оε_r, где ε_о =10 ^{- 9} /(36π), получим для 1 км кабеля, Ф/км,

(1.1)

Соответственно G= ωΡtgδ, См/км, где ε_rи tgδ - диэлектрическая проницаемость и тангенс угла диэлектрических потерь; а - расстояние между проводниками; r - радиус проводника.

Реальные конструкции симметричных кабелей, как правило, содержат много пар и находятся в общих металлических оболочках. С учетом близости соседних пар и влияния наружной металлической оболочки емкость симметричных кабелей для различных типов скрутки рассчитывают по следующей формуле, Ф/км:

С= ε_r 10 ^{- 6} / [36 ln(aψ/r)], (1.2)

где - коэффициент скрутки кабельных цепей (1,02 … 1,07); ε_r- эффективная диэлектрическая проницаемость изоляции; ψ - поправочный коэффициент, характеризующий близость металлической оболочки проводников.

Расчетные формулы коэффициента ψ для различных видов группообразования кабелей приведены ниже:

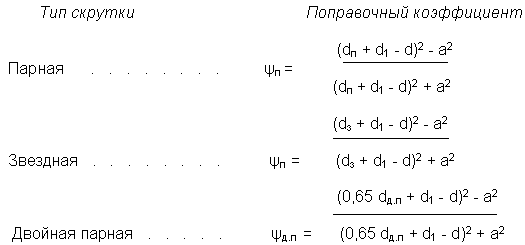
При расчете проводимости изоляции G следует, кроме проводимости, обусловленной диэлектрическими потерями, учитывать также проводимость, обусловленную утечкой тока в силу несовершенства диэлектрика: G₀=1/R_из ._.

По величине эта проводимость изоляции обратно пропорциональна сопротивлению изоляции кабеля (линии). В результате проводимость изоляции кабельной цепи, См/м,

G=G₀+G_f=1/R_из.=ωΡtgδ. (1.3)

При расчете проводимости изоляции кабельных линий учитывают, что по абсолютной величине потери в диэлектрике при переменном G_f существенно больше, чем при постоянном токе G₀, по этому проводимость в кабельных линиях рассчитывают по формуле G=G_f.=ωΡtgδ. При рассчете проводимости изоляции по постоянному току G₀ принимают: для городских телефонных кабелей R_и= 2 000 МОм·км, а для кабелей дальней связи - 10 000 МОм·км.

Кабели связи, как правило, имеют сложную комбинированную изоляцию, состоящую из твердого диэлектрика (бумаги, стирофлекса, полиэтилена и др.) и воздуха. Результирующие эквивалентные значения диэлектрической проницаемости ε_э.и угла диэлектрических потерь tgδ_э сложной изоляции определяются электрическими свойствами и соотношением объемов составных ее частей. Причем эквивалентные значения ε_э.и tgδ_э сложной изоляции близки к величинам ε и tgδ той части изоляции, которая занимает большой объем.

Рассмотрим графики зависимости первичных параметров линий связи R, L, C, G от частоты, диаметра проводника и расстояния между проводниками.

С увеличением частоты значение параметров R и G возрастает за счет потерь в проводниках на вихревые токи и в изоляции на диэлектрическую поляризацию, а индуктивность L уменьшается,так как из-за поверхностного эффекта уменьшается внутренняя индуктивность проводника. Емкость C от частоты не зависит.

При увеличении расстояния между проводниками параметры R, C, G закономерно уменьшаются, а индуктивность L возрастает. Снижение R обусловлено уменьшением потерь на эффект близости. Рост L связан с увеличением площади контура, пронизываемого магнитным потоком. Емкость C уменьшается, так как проводники удаляются друг от друга и уменьшается их взаимодействие.

С увеличением диаметра проводников параметры C и G растут, а L уменьшается. Изменение активного сопротивления имеет сложный характер. Это обусловлено тем, что с увеличением диаметра проводника сопротивление постоянному току резко уменьшается, а сопротивление за счет поверхностного эффекта и эффекта близости растет. Поэтому вначале R снижается резко, а затем снижение замедляется.

Порядок величин первичных параметров существующих типов линий связи следующий: R=5 . . . 200Ом/км; L=0,6 … 2 мГн/км; С=5… 50 мФ/км; G=1 … 200 мкСм/км. В кабельных линиях за счет тонких проводников и близкого их расположения превалируют параметры R и C. Емкость кабеля в 3…5 раз больше емкости воздушной линии, а активное сопротивление - в 5…10 раз. Индуктивность кабеля, наоборот, меньше в 2…3 раза.

Теоретически от температуры зависят все четыре первичных параметра. Однако практически следует учитывать лишь температурную зависимость активного сопротивления. Изменение от температуры L, C, G весьма незначительно.

Температурная зависимость активного сопротивления цепи определяется по формуле

R_t=R₂₀[1+α_R(t-20)], (2.1)

где R_t - сопротивление при температуре t˚ C; R₂₀- тоже при температуре 20˚С;

α_R - температурный коэффициент сопротивления, равный для меди 0,004 и для алюминия 0,0037.

С увеличением сопротивление цепи растет. Физически это объясняется тем, что с увеличением температуры возрастает хаотическое движение атомов решетки и затрудняется прохождение электронов через нее.

Вторичные параметры симметричных цепей Z_в, α, β, υ рассчитываются по формулам, приведенным ранее в таблице. В ряде случаев вторичные параметры выражают непосредственно через параметры цепей (a,d) и качество исходных материалов (ε, tgα).

Подставив в формулу Z_в =√L/C значения L и C получим значение волнового сопротивления симметричной цепи, Ом,

Коэффициент затухания симметричной цепи с медными проводниками, дБ/км,

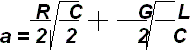
Путем подстановки в эту формулу значений первичных параметров:

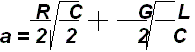(2.2)

Коэффициент фазы, рад/км, определяется формулой

β=ω√LC или β=ω√ε/c , (2.3)

где с- скорость света , равна 30 000 км/с.

Скорость распространения энергии, км/с,

υ=1√LC=с/√ε. (2.4)

Типовые частотные зависимости вторичных параметров цепи распространяются и на симметричные цепи.

5. Теория передачи по линиям связи

5.1. Исходные положения

Строгое решение задач распространения электромагнитной энергии по направляющим системам (кабелей, волноводы, световоды и т.д.) требует применения классической электродинамики и управлений Максвелла. На основе электродинамики можно рассмотреть практически все вопросы передачи, излучения, влияния, поглощения, экранирования в любых направляющих системах при различных диапазонах частот и скоростях передачи.

Правда, во многих случаях очень сложно искать точные решения на базе электродинамики. Под влиянием запросов практики в свое время были разработаны приближенные методы решения задач различных классов. Такими наиболее характерными методами являются методы теории цепей и, с другой стороны, теории лучевой оптики. В первом случае (квазистационарный режим) совершается переход от волновых электродинамических процессов к колебательным (λ >> D), а во втором случае (квазиоптический режим) – к лучевым процессам (λ<<D). При λ >> D в области сравнительно низких частот (до 10⁸ Гц) справедливы методы теории цепей и уравнения однородной линии. При λ<<D в области очень высоких частот (свыше 10¹³ Гц) справедливы уравнения лучевой оптики.

Однако оба эти режима являются предельными случаями строгих уравнений электродинамики, поэтому курс технической электродинамики (ТЭД) является основным (базовым) аппаратом изучения, исследования и расчета направляющих систем передачи.

5.2. Уравнения однородной линии

Качество передачи по линейным цепям связи и их электрические свойства полностью характеризуются первичными параметрами. По физической природе параметры цепи связи аналогичны параметрам колебательных контуров, составленных из элементов R, L, C. Разница состоит лишь в том, что в контурах эти параметры являются сосредоточенными, а в цепях связи они равномерно распределены по всей длине линий. Параметры R и L, включенные последовательно (продольные), образуют суммарное сопротивление Z=R+iωL, а параметры G и C (поперечные) – суммарную проводимость Y=G+iωC. Из указанных четырех параметров лишь R и C обусловливают потери энергии: первый – тепловые потери в проводах и других металлических частях кабеля (экран, оболочка, броня); второй – потери в изоляции.

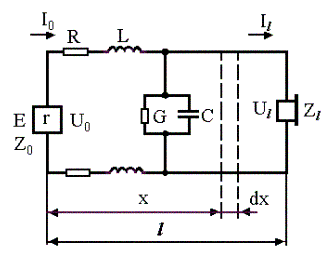
Рис 2.1

Рассмотрим однородную цепь связи с первичными параметрами R, L, C и G (рис. 2.1). В начале цепи имеется генератор с сопротивлением Z₀, в конце – нагрузка Z_l. Обозначим напряжение и ток в начале цепи U₀L₀, в конце – U_lL_l. Выделим на расстоянии x от начала цепи бесконечно малый участок dx. Обозначим ток, проходящий по элементу цепи dx, I и напряжение между проводами через U. Тогда падение напряжения на участке dx будет равно: - dU/dx=I(R+iωL). Σтечка тока на участке: - dI/dx=U(G+iωC).

Произведя соответствующие преобразования и имея в виду, что ch x=(е^γx+е^–γx)/2 и sh x=( е^γx–е^–γx)/2, получим значения напряжения U_x и тока I_x в любой точке цепи x:

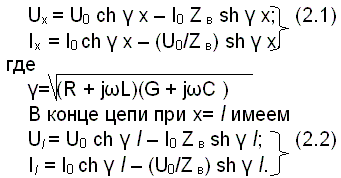
Практически оказывается удобнее пользоваться выражениями, устанавливающими зависимость напряжения и тока в начале цепи от напряжения и тока в конце цепи. Тогда, решая предыдущею систему относительно U₀ и I₀, получаем:

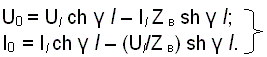(2.3)

Уравнения (2.1) – (2.3) устанавливают взаимную связь токов и напряжений с параметрами цепи R, L, C и G или γ и Z _в и позволяют определить напряжения и ток в любой точке цепи в зависимости от значений U и I в начале или конце ее. Эти уравнения справедливы при любых нагрузках (Z ₀ и Z _l) на концах цепи.

При согласованных нагрузках Z ₀ =Z _l =Z _в и U₀/I₀ = =U_l/I_l = Z _в уравнения (2.1) - (2.3) упрощаются и принимают вид:

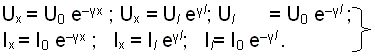(2.4)

Практически наиболее часто пользуются уравнениями в виде U₀/U_l = е^γl и I₀/I_l = е^γl . Аналогично для мощности P=UI получим P₀/P_l = е^2γl. Таким образом, получены уравнения однородной цепи в общем виде при любых нагрузках по концам и при согласованных нагрузках.

Из приведенных формул следует, что распространение энергии по линии, ток и напряжение в любой точке цепи обусловлены в первую очередь параметрами γ и Z _в.

5.3. Волновое сопротивление

Волновое (характеристическое) сопротивление Z _в и коэффициент распространения γ являются вторичными параметрами линии и широко используются для оценки эксплуатационно-технических качеств линии связи. Волновое сопротивление – это сопротивление, которое встречает электромагнитная волна при распространении вдоль однородной линии без отражения, т. е. при условии, что на процесс передачи не влияют несогласованности на концах линии. Оно свойственно данному типу кабеля и зависит лишь от его первичных параметров и частоты передаваемого тока.

Электромагнитную волну можно представить в виде двух волн: волны напряжения, соответствующей электрической энергии, и волны тока, соответствующей магнитной энергии. Количественное соотношение, имеющее место между волной напряжения и волной тока в линии, и есть волновое сопротивление цепи. При этом, как следует из данного выше определения волнового сопротивления, необходимо рассматривать лишь падающую (движущуюся вперед) электромагнитную волну: Z _в=U_n/I_n. Если в линии выделить отдельно отраженную волну, то она, двигаясь к началу линии, также будет встречать сопротивление, равное волновому сопротивлению: Z _в=U₀/I₀.

Волновое сопротивление рассчитывается по формуле

По своей физической природе, что также следует из приведенной формулы, величина Z _в не зависит от длины волны и постоянна в любой точке цепи.

В общем виде волновое сопротивление является комплексной величиной и может быть выражено через его действительную и мнимую части:

Z _в = |Z _в| е^iφ_в = |Z _в| cos φ_в + i |Z _в| sin φ_в.

5.4. Коэффициент распространения

Электромагнитная энергия, распространяясь вдоль линии, уменьшается по величине от начала к концу линии. Ослабление или затухание энергии объясняется потерями ее в цепи передачи. Следует различать два вида потерь энергии: в металле и в диэлектрики. При прохождение тока по кабельной цепи происходит нагревание токопроводящих жил и создаются тепловые потери энергии. С ростом частоты эти потери увеличиваются: чем больше активное сопротивление цепи, тем больше потери энергии в металле. Потери энергии в диэлектрике обусловлены несовершенством применяемых диэлектриков (бумаги, резины и др.) и затратами энергии на диэлектрическую поляризацию (G=ωC tgδ). Βсе эти потери учитываются посредством коэффициента распространения γ.

Коэффициент распространения γ является комплексной величиной и может быть представлен в виде суммы действительной и мнимой частей ее:

Уравнение для токов и напряжения можно представить в следующем виде:

U₀/U_l = I₀/I_l = е^{(α + i β) l} = е^{α l} е ^{i βl} = A е ^{i φ} .

Модуль этого выражения А= е^αl характеризует уменьшение абсолютного значения тока или напряжения при прохождении по линии длиной l. Угол φ=βl характеризует изменение угла векторов тока или напряжения на этом же участке линии длиной l.

Аналогичные выражения для мощностей имеют вид

P₀/P_l = е^2γl = е^{2α l} е ^{i 2βl} .

Следовательно, действительная часть – αl коэффициента распространения показывает уменьшение электромагнитной энергии в конце линии по сравнению с началом:

|U₀/U_l| = |I₀/I_l|= е^{α l} ; P₀/P_l = е^2αl .

Мнимая часть выражения – βl показывает изменение фазы (угла) при распространении энергии по цепи:

βl = φ_0U – φ_lU = φ_0I – φ_lI; 2βl = φ_0P – φ_lP .

При передаче сигналов связи параметры α и β характеризуют соответственно затухание и изменение фаз тока, напряжения и мощности на участке кабельной цепи длиной 1 км и называются коэффициентом затухания и коэффициентом фазы. Коэффициент распространения γ = α + i β одновременно определяет изменение сигнала как по абсолютной величине, так и по фазе на 1 км длины кабеля.

Логарифмируя обе части приведенных выше выражений, получаем формулы для расчета величины затухания:

αl = ln |U₀/U_l| = ln |I₀/I_l| ; αl = [ln (P₀/P_l)]/2.

Затухание цепи по связи (α = αl) принято оценивать в децибелах (белах) или неперах. Для децибелов (белов) используется десятичная система логарифмов, а для неперов – натуральная.

Затухание в 1 бел (Б) соответствует уменьшению мощности в 10 раз, а ток или напряжения – в 3,17 раз.

5.5. Скорость распространения электромагнитной энергии по цепям связи

Электромагнитная энергия распространяется по линии с определенной скоростью. Посланный в линию сигнал достигает конца ее лишь через соответствующий промежуток времени. Скорость передачи зависит от параметров цепи и частоты тока. Она определяется из выражения υ = ω/β.

Из этой формулы видно, скорость распространения является функцией частоты f = ω/2π и коэффициент фазы β, который в свою очередь зависит от первичных параметров линии. Таким образом, если затухание цепи определяет качество и дальность связи, то коэффициент фазы β обусловливает скорость движения энергии по линии.

В диапазоне высоких частот, когда β = ω√ LC , скорость не зависит от частоты и определяется лишь параметрами кабеля:

.

При постоянном токе

На рис. представлена частотная зависимость скорости распространения электромагнитной энергии по кабельным линиям с диаметром токопроводящих жил 1,2 мм.

Анализируя приведенные выше формулы и кривые, можно отметить, что с возрастанием частоты скорость распространения электромагнитной энергии по кабельным линиям также существенно возрастает. Скорость распространения электромагнитной энергии по линии при постоянном токе составляет примерно 10 000 км/c, а при токах высоких частот имеет величину порядка 250 000 км/с, приближаясь к скорости света (c=300 000 км/с).