9.1. Бинарные последовательности с непротивоположными символами
Хотя бинарные m–последовательности и последовательности Лежандра наряду с тремя другими классами бинарных кодов обладают максимальным периодическим боковым лепестком ![]() , снижающимся с ростом длины, все же вероятны ситуации, когда нужное значение
, снижающимся с ростом длины, все же вероятны ситуации, когда нужное значение ![]() для них можно получить лишь за счет неприемлемо больших длин
для них можно получить лишь за счет неприемлемо больших длин ![]() . К примеру, для многих локаторов, сонаров и других дальномерных систем требование временного разрешения сигналов в динамическом диапазоне более 80 дБ является вполне рутинным. Для его выполнения на основе оптимальных бинарных кодов длины последних должны превышать
. К примеру, для многих локаторов, сонаров и других дальномерных систем требование временного разрешения сигналов в динамическом диапазоне более 80 дБ является вполне рутинным. Для его выполнения на основе оптимальных бинарных кодов длины последних должны превышать ![]() , что может неоправданно замедлить процедуру начального поиска. Разумеется, во многих подобных сценариях наилучшим выбором были бы последовательности с идеальной ПАКФ, которая, однако, нереализуема на множестве бинарных кодов, традиционно считающихся наиболее привлекательными технологически. В настоящем разделе анализируются возможности осуществления идеальной периодической АКФ в случаях, когда алфавит последовательности не ограничен рамками противоположной бинарной пары
, что может неоправданно замедлить процедуру начального поиска. Разумеется, во многих подобных сценариях наилучшим выбором были бы последовательности с идеальной ПАКФ, которая, однако, нереализуема на множестве бинарных кодов, традиционно считающихся наиболее привлекательными технологически. В настоящем разделе анализируются возможности осуществления идеальной периодической АКФ в случаях, когда алфавит последовательности не ограничен рамками противоположной бинарной пары ![]() .
.
9.1. Бинарные последовательности с непротивоположными символами
Замена противоположного алфавита ![]() на некоторый бинарный непротивоположный позволяет обратить в нуль все периодические боковые лепестки любой бинарной минимаксной последовательности. Простейший путь построения упомянутого алфавита – добавление константы
на некоторый бинарный непротивоположный позволяет обратить в нуль все периодические боковые лепестки любой бинарной минимаксной последовательности. Простейший путь построения упомянутого алфавита – добавление константы ![]() (в общем случае комплексной) к начальной
(в общем случае комплексной) к начальной ![]() последовательности
последовательности ![]() с заменой тем самым символов +1 и –1 на
с заменой тем самым символов +1 и –1 на ![]() и
и ![]() соответственно. Периодическая АКФ модифицированной таким образом последовательности вычисляется непосредственно:
соответственно. Периодическая АКФ модифицированной таким образом последовательности вычисляется непосредственно:
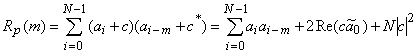 ,
,
где 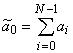 , как обычно, постоянная составляющая исходной последовательности
, как обычно, постоянная составляющая исходной последовательности ![]() .
.
Для любой минимаксной последовательности 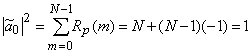 , т.е.
, т.е. ![]() . Так как изменение знака всех элементов последовательности не меняет АКФ, можно, не ограничивая общности, считать
. Так как изменение знака всех элементов последовательности не меняет АКФ, можно, не ограничивая общности, считать ![]() . Поэтому, потребовав равенства боковых лепестков последовательности
. Поэтому, потребовав равенства боковых лепестков последовательности ![]() нулю и учитывая минимаксные свойства исходной последовательности, получаем уравнение для комплексной неизвестной
нулю и учитывая минимаксные свойства исходной последовательности, получаем уравнение для комплексной неизвестной ![]() :
:
![]() .
.
Найдем потенциально наиболее интересные решения последнего уравнения. Когда желателен действительный алфавит, ![]() , то имеем квадратное уравнение
, то имеем квадратное уравнение
![]()
с корнями ![]() . Новые бинарные непротивоположные символы
. Новые бинарные непротивоположные символы ![]() и
и ![]() теперь можно поделить на
теперь можно поделить на ![]() с целью сохранения +1 как символа нового алфавита. После этого правило преобразования бинарной минимаксной последовательности в последовательность с идеальной АКФ предстает в виде: все символы –1 заменяются на
с целью сохранения +1 как символа нового алфавита. После этого правило преобразования бинарной минимаксной последовательности в последовательность с идеальной АКФ предстает в виде: все символы –1 заменяются на
![]() ,
,
тогда как все элементы +1 остаются без изменения.
Описанное решение приводит к алфавиту из двух противоположных символов разной амплитуды, т.е. к амплитудной модуляции (см. рисунок (a)).
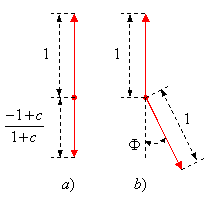
Альтернативным решением служит непротивоположный ФМ алфавит, к которому легко прийти, положив ![]() чисто мнимым:
чисто мнимым: ![]() . Тогда имеет решения
. Тогда имеет решения ![]() , а новые символы
, а новые символы ![]() и
и ![]() после деления на
после деления на ![]() принимают вид 1 и
принимают вид 1 и ![]() , где
, где ![]() (рисунок (b)).
(рисунок (b)).
Представленный непритязательный способ преобразования алфавита, едва ли можно признать эффективным в практическом отношении. Как видно, его результатом являются довольно экзотические значения комплексных амплитуд кода, установка и поддержание которых с требуемой точностью технологически достаточно проблематичны.
9.2. Многофазные коды
На основе небинарной (![]() ) ФМ можно строить разнообразные многофазные последовательности с идеальной периодической АКФ. Известен ряд правил их конструирования, которые в большей или меньшей степени родственны двум наиболее популярным алгоритмам. Первый из них, приводящий к кодам Чу (или квадратичных вычетов), состоит в прямой дискретной аппроксимации закона линейной частотной модуляции. Код Чу существует для любой длины
) ФМ можно строить разнообразные многофазные последовательности с идеальной периодической АКФ. Известен ряд правил их конструирования, которые в большей или меньшей степени родственны двум наиболее популярным алгоритмам. Первый из них, приводящий к кодам Чу (или квадратичных вычетов), состоит в прямой дискретной аппроксимации закона линейной частотной модуляции. Код Чу существует для любой длины ![]() и генерируется как
и генерируется как
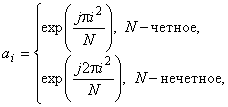
![]() .
.
Хотя коды Чу служат достаточно красивым академическим примером ФМ последовательностей с идеальной АКФ, их практическая ценность далеко не бесспорна, поскольку объем фазового алфавита для них линейно растет с длиной, и при значительных ![]() интервал между соседними фазами становится чрезвычайно малым. Из-за этого требования к точности установки и поддержания значений фаз, устойчивости к влиянию окружающей среды и т.п. могут оказаться технологически невыполнимыми.
интервал между соседними фазами становится чрезвычайно малым. Из-за этого требования к точности установки и поддержания значений фаз, устойчивости к влиянию окружающей среды и т.п. могут оказаться технологически невыполнимыми.
Аналогичные оговорки (хотя и в меньшей степени) справедливы и в отношении другого часто упоминаемого семейства многофазных последовательностей: кодов Франка. Последние также базируются на ступенчатой аппроксимации линейной частотной модуляции, однако значительно более грубой, и существуют только для длин, являющихся квадратами целых чисел ![]() . Правило их генерирования имеет вид
. Правило их генерирования имеет вид
![]() ,
,
где, как обычно, ![]() символизирует округление неотрицательного
символизирует округление неотрицательного ![]() в сторону нуля.
в сторону нуля.
Из сравнения правил формирования видно, что фазовый шаг алфавита для кодов Франка меньше чем для кодов Чу в ![]() раз, так что объем алфавита первых растет с длиной
раз, так что объем алфавита первых растет с длиной ![]() значительно медленнее.
значительно медленнее.
9.3. Троичные последовательности
Перейдем к рассмотрению последовательностей, чьи элементы ![]() могут принимать наряду с бинарными значениями
могут принимать наряду с бинарными значениями ![]() еще и нулевое. Другими словами, введем троичный алфавит
еще и нулевое. Другими словами, введем троичный алфавит ![]() , технически означающий комбинирование бинарной ФМ с паузами, т.е. интервалами времени, в течение которых чипы отсутствуют. Нетрудно понять, что расширение бинарного алфавита
, технически означающий комбинирование бинарной ФМ с паузами, т.е. интервалами времени, в течение которых чипы отсутствуют. Нетрудно понять, что расширение бинарного алфавита ![]() до троичного
до троичного ![]() не ведет к сколько-нибудь ощутимым усложнениям в части формирования и обработки сигнала, однако оно, как показано ниже, открывает дорогу к построению последовательностей с идеальными периодическими корреляционными свойствами. Единственным отрицательным моментом перехода к новому алфавиту следует считать снижение эффективности распределения энергии во времени, обусловленное введением
не ведет к сколько-нибудь ощутимым усложнениям в части формирования и обработки сигнала, однако оно, как показано ниже, открывает дорогу к построению последовательностей с идеальными периодическими корреляционными свойствами. Единственным отрицательным моментом перехода к новому алфавиту следует считать снижение эффективности распределения энергии во времени, обусловленное введением ![]() пауз на периоде последовательности
пауз на периоде последовательности ![]() , которое может быть оценено величиной пик–фактора излучения, т.е. отношением пиковой мощности к средней:
, которое может быть оценено величиной пик–фактора излучения, т.е. отношением пиковой мощности к средней: ![]() .
.
Следовательно, желательно отыскание троичных последовательностей, имеющих не только идеальную периодическую АКФ, но и малое число нулей ![]() на периоде, т.е. пик-фактор, незначительно превышающий единицу. Без подобного ограничения задача вырождается и имеет тривиальное решение: код с единственным ненулевым символом на периоде
на периоде, т.е. пик-фактор, незначительно превышающий единицу. Без подобного ограничения задача вырождается и имеет тривиальное решение: код с единственным ненулевым символом на периоде ![]() , соответствующий одиночному чипу, повторяющемуся с периодом
, соответствующий одиночному чипу, повторяющемуся с периодом ![]() , безусловно обладает идеальной периодической АКФ, не представляя никакой ценности с точки зрения технологии расширенного спектра.
, безусловно обладает идеальной периодической АКФ, не представляя никакой ценности с точки зрения технологии расширенного спектра.
К настоящему моменту известен ряд правил генерирования троичных последовательностей с заявленными свойствами. Наиболее мощное из них порождает последовательности, длина и пик-фактор которых даются соотношениями
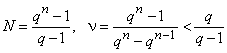 ,
,
где ![]() – натуральная степень простого числа
– натуральная степень простого числа ![]() , а
, а ![]() – нечетное натуральное. Последовательности этого типа определены для любой комбинации
– нечетное натуральное. Последовательности этого типа определены для любой комбинации ![]() в пределах оговоренных ограничений и, следовательно, выбором достаточно большого
в пределах оговоренных ограничений и, следовательно, выбором достаточно большого ![]() значение их пик-фактора можно сделать сколь угодно близким к единице.
значение их пик-фактора можно сделать сколь угодно близким к единице.
В наиболее простой форме конструирование троичных последовательностей с указанными параметрами удается описать, опираясь на ![]() -ичные
-ичные ![]() -последовательности. Пусть
-последовательности. Пусть ![]() –
– ![]() -ичная
-ичная ![]() -последовательность, где
-последовательность, где ![]() – простое нечетное. Каждый ее символ является элементом простого поля
– простое нечетное. Каждый ее символ является элементом простого поля ![]() . Преобразуем данную последовательность в троичную, отображая нулевой элемент в действительный нуль, а ненулевые элементы в их двузначные характеры. После этого поменяем знаки всех элементов на нечетных позициях. Описанный алгоритм формализуется как
. Преобразуем данную последовательность в троичную, отображая нулевой элемент в действительный нуль, а ненулевые элементы в их двузначные характеры. После этого поменяем знаки всех элементов на нечетных позициях. Описанный алгоритм формализуется как
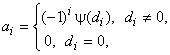 ,
,
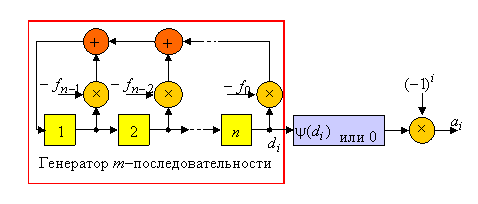
где ![]() . На следующем рисунке приведена структура, реализующая данное правило, которая содержит генератор
. На следующем рисунке приведена структура, реализующая данное правило, которая содержит генератор ![]() -последовательности, блок отображения элементов
-последовательности, блок отображения элементов ![]() -последовательности в значения характера или нуль, и умножитель, осуществляющий коммутацию полярности нечетных символов.
-последовательности в значения характера или нуль, и умножитель, осуществляющий коммутацию полярности нечетных символов.
Пример 9.3.1. Пусть ![]() . Тогда с помощью примитивного над полем
. Тогда с помощью примитивного над полем ![]() полинома
полинома ![]() может быть построена m–последовательность
может быть построена m–последовательность ![]() длины
длины ![]() , задаваемая линейной рекурсией
, задаваемая линейной рекурсией ![]() . При начальном состоянии регистра
. При начальном состоянии регистра ![]() генерируется последовательность:
генерируется последовательность: ![]() .
.
В поле ![]() имеются только два ненулевых элемента, из которых лишь элемент 2 примитивен. Очевидно,
имеются только два ненулевых элемента, из которых лишь элемент 2 примитивен. Очевидно, ![]() и, следовательно, ненулевые элементы
и, следовательно, ненулевые элементы ![]() -последовательности заменяются по правилу
-последовательности заменяются по правилу ![]() ,
, ![]() , а нули отображаются в вещественный нуль. В результате получается троичная последовательность периода 26
, а нули отображаются в вещественный нуль. В результате получается троичная последовательность периода 26
![]() .
.
Изменение знаков элементов с нечетными номерами (начиная с нуля) приводит последовательность к окончательному виду
![]() .
.
Полученная троичная последовательность имеет период ![]() и пик-фактор
и пик-фактор ![]() . Вид ПАКФ иллюстрирует следующий рисунок.
. Вид ПАКФ иллюстрирует следующий рисунок.
9.4. Подавление боковых лепестков вдоль оси запаздываний
Предположим, что проектировщик системы не склонен отказываться от бинарных ![]() последовательностей и, в то же время, не удовлетворен достижимым для них уровнем боковых лепестков периодической АКФ
последовательностей и, в то же время, не удовлетворен достижимым для них уровнем боковых лепестков периодической АКФ ![]() . В подобных обстоятельствах эффективно разрешить эти противоречивые запросы, можно «имитацией» идеальной периодической АКФ за счет отказа от согласованной фильтрации в пользу специальной рассогласованной обработки, устраняющей боковые лепестки на всем периоде сигнала.
. В подобных обстоятельствах эффективно разрешить эти противоречивые запросы, можно «имитацией» идеальной периодической АКФ за счет отказа от согласованной фильтрации в пользу специальной рассогласованной обработки, устраняющей боковые лепестки на всем периоде сигнала.
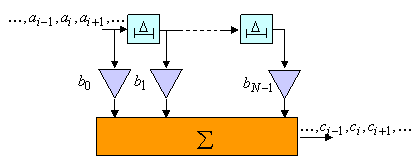
Рассмотрим некоторую последовательность ![]() периода
периода ![]() , которая манипулирует чипы длительности
, которая манипулирует чипы длительности ![]() , и фильтр с конечным импульсным откликом, осуществляющий суммирование
, и фильтр с конечным импульсным откликом, осуществляющий суммирование ![]() сигнальных копий, задержанных на
сигнальных копий, задержанных на ![]() и взвешенных коэффициентами
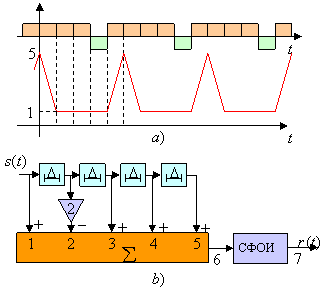
и взвешенных коэффициентами ![]() , как показано на рисунке слева. При подаче на вход последовательности
, как показано на рисунке слева. При подаче на вход последовательности ![]() , отклик фильтра описывается последовательностью
, отклик фильтра описывается последовательностью ![]() , элементы которой находятся сверткой
, элементы которой находятся сверткой
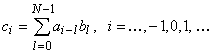
Наложим на фильтр следующие требования
![]() ,
,
означающие физически, что выходной сигнал фильтра имеет ненулевые главные пики, повторяющиеся с периодом ![]() , тогда как все боковые лепестки между ними равны нулю. Подобный фильтр, называемый далее фильтром подавления боковых лепестков (ФПБЛ), имитирует своим откликом идеальную периодическую АКФ. В связи с нереализуемостью (за единственным тривиальным исключением) идеальной периодической АКФ в классе бинарных кодов ФПБЛ оказывается рассогласованным и, следовательно, проигрывает согласованному фильтру в выходном отношении сигнал-шум.
, тогда как все боковые лепестки между ними равны нулю. Подобный фильтр, называемый далее фильтром подавления боковых лепестков (ФПБЛ), имитирует своим откликом идеальную периодическую АКФ. В связи с нереализуемостью (за единственным тривиальным исключением) идеальной периодической АКФ в классе бинарных кодов ФПБЛ оказывается рассогласованным и, следовательно, проигрывает согласованному фильтру в выходном отношении сигнал-шум.
Кратчайший путь отыскания коэффициентов фильтра в явном виде – применение дискретного преобразования Фурье (ДПФ). Последовательность ![]() и компоненты ее ДПФ-спектра
и компоненты ее ДПФ-спектра ![]() связаны друг с другом прямым и обратным ДПФ:
связаны друг с другом прямым и обратным ДПФ:
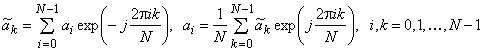 .
.
Наша цель – получение на выходе фильтра дискретной дельта-функции, имеющей единственный ненулевой элемент на периоде. Спектр такой последовательности равномерен: ![]() . Тогда на основании теоремы о свертке спектр последовательности на выходе фильтра
. Тогда на основании теоремы о свертке спектр последовательности на выходе фильтра ![]() , где спектр последовательности коэффициентов фильтра
, где спектр последовательности коэффициентов фильтра ![]() есть не что иное, как передаточная функция ФПБЛ:
есть не что иное, как передаточная функция ФПБЛ:
![]() .
.
Как показывает последнее равенство, ФПБЛ физически реализуем для любой периодической последовательности, ДПФ-спектр которой не содержит нулевых компонент. Вычислив обратное ДПФ, приходим к явному выражению для коэффициентов ФПБЛ
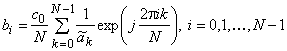 .
.
Как известно, согласованная обработка обеспечивает максимум отношения сигнал–шум на выходе фильтра. Очевидно, что использование ФПБЛ, отличающегося от СФ, приведет к энергетическим потерям, которые и служат платой за достижение идеальности сжатия. Оценим величину потерь в отношении сигнал-шум.
Если бы фильтр был согласованным, его коэффициенты составляли бы последовательность, зеркальную ко входной: ![]() , и амплитуда выходной последовательности оказалась бы равной
, и амплитуда выходной последовательности оказалась бы равной 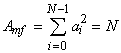 , поскольку входная последовательность – бинарная. Для входного шума, имеющего время корреляции в пределах
, поскольку входная последовательность – бинарная. Для входного шума, имеющего время корреляции в пределах ![]() и дисперсию
и дисперсию ![]() , дисперсия на выходе согласованного фильтра
, дисперсия на выходе согласованного фильтра 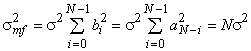 . Таким образом, отношение сигнал-шум по мощности
. Таким образом, отношение сигнал-шум по мощности ![]() на выходе согласованного фильтра
на выходе согласованного фильтра
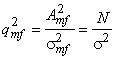 .
.
Подобным же образом, амплитуда выходной последовательности ФПБЛ ![]() , а дисперсия шума
, а дисперсия шума
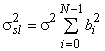 .
.
С учетом связи между периодической АКФ произвольной последовательности и ее энергетического спектра, а также выражения для спектра коэффициентов фильтра ![]() получаем следующее выражение для дисперсии шума на выходе фильтра
получаем следующее выражение для дисперсии шума на выходе фильтра
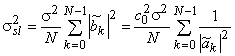 ,
,
после чего отношение сигнал-шум по мощности ![]() на выходе ФПБЛ принимает вид
на выходе ФПБЛ принимает вид
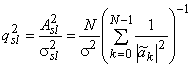 .
.
Теперь можно рассчитать энергетические потери ![]() ФПБЛ по отношению к согласованному фильтру как
ФПБЛ по отношению к согласованному фильтру как
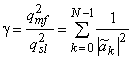 .
.
Следовательно, потери ФПБЛ в отношении сигнал-шум ![]() определяются неравномерностью энергетического спектра
определяются неравномерностью энергетического спектра ![]() входной последовательности
входной последовательности
Возможность устранения всех периодических боковых лепестков по существу означает ориентацию на новый критерий синтеза бинарных последовательностей, альтернативный минимизации максимального бокового лепестка ![]() . Более естественной представляется минимизация цены устранения боковых лепестков, которой, разумеется, являются потери в отношении сигнал-шум
. Более естественной представляется минимизация цены устранения боковых лепестков, которой, разумеется, являются потери в отношении сигнал-шум ![]() .
.
Как и во многих задачах, касающихся бинарных последовательностей, глобально оптимальная бинарная последовательность фиксированной длины ![]() с минимальными потерями
с минимальными потерями ![]() может быть найдена только полным перебором. Разумеется, экспоненциальный рост необходимого вычислительного ресурса препятствует продвижению поиска далеко за рамки указанного диапазона. Однако на данный момент известны многие регулярные правила построения бинарных последовательностей сколь угодно большой длины с очень малыми потерями
может быть найдена только полным перебором. Разумеется, экспоненциальный рост необходимого вычислительного ресурса препятствует продвижению поиска далеко за рамки указанного диапазона. Однако на данный момент известны многие регулярные правила построения бинарных последовательностей сколь угодно большой длины с очень малыми потерями ![]() (хотя и без гарантии их глобальной оптимальности).
(хотя и без гарантии их глобальной оптимальности).
Рассмотрим специальный класс бинарных последовательностей с двухуровневой периодической АКФ, т.е. постоянным уровнем ![]() боковых лепестков
боковых лепестков
![]()
Для последовательностей данного типа
![]() ,
,
где ![]() – нормированный уровень бокового лепестка АКФ, а коэффициенты ФПБЛ определяются соотношением
– нормированный уровень бокового лепестка АКФ, а коэффициенты ФПБЛ определяются соотношением
![]() .
.
Первое слагаемое правой части этого равенства соответствует последовательности ![]() , считываемой справа налево, т.е. коэффициентам согласованного фильтра. Таким образом, для последовательности с двухуровневой АКФ ФПБЛ можно получить, слегка модифицируя согласованный фильтр вычитанием из всех его коэффициентов определенной константы. Более того, для бинарных последовательностей этого класса коэффициенты ФПБЛ принимают лишь два возможных значения
, считываемой справа налево, т.е. коэффициентам согласованного фильтра. Таким образом, для последовательности с двухуровневой АКФ ФПБЛ можно получить, слегка модифицируя согласованный фильтр вычитанием из всех его коэффициентов определенной константы. Более того, для бинарных последовательностей этого класса коэффициенты ФПБЛ принимают лишь два возможных значения ![]() , где
, где ![]() – по-прежнему постоянная составляющая последовательности, т.е. разность между количествами положительных и отрицательных единиц на периоде:
– по-прежнему постоянная составляющая последовательности, т.е. разность между количествами положительных и отрицательных единиц на периоде: ![]() .
.
Пример 9.4.1. Построим ФПБЛ для периодического бинарного кода Баркера длины ![]() :
: ![]() , для которого
, для которого ![]() , и постоянная составляющая
, и постоянная составляющая ![]() . Периодическая АКФ такого кода, как легко поверить непосредственно, является двухуровневой с
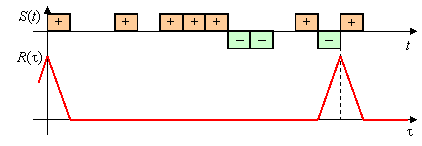
. Периодическая АКФ такого кода, как легко поверить непосредственно, является двухуровневой с ![]() . На рисунке (a) показана ПАКФ (т.е. отклик согласованного фильтра) периодического сигнала с прямоугольными чипами, модулированного рассматриваемым кодом. Согласованный фильтр для данной последовательности легко трансформируется в ФПБЛ заменой коэффициентов +1 на
. На рисунке (a) показана ПАКФ (т.е. отклик согласованного фильтра) периодического сигнала с прямоугольными чипами, модулированного рассматриваемым кодом. Согласованный фильтр для данной последовательности легко трансформируется в ФПБЛ заменой коэффициентов +1 на ![]() и –1 на
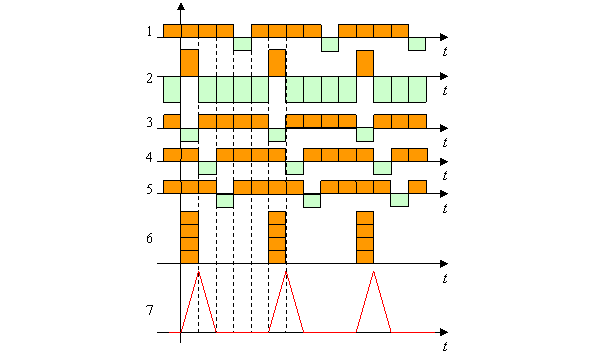
и –1 на ![]() , которая с соответствующим масштабированием равносильна замене –1 на –2 при неизменности всех коэффициентов +1 (см. рисунок (b). Отклик ФПБЛ на данный сигнал построен на рисунке следующего слайда, на котором оцифровка диаграмм соответствует точкам схемы. Выходной сигнал фильтра имеет желаемую форму, т.е. нулевой уровень боковых лепестков. Легко подсчитать, что энергетические потери в ФПБЛ
, которая с соответствующим масштабированием равносильна замене –1 на –2 при неизменности всех коэффициентов +1 (см. рисунок (b). Отклик ФПБЛ на данный сигнал построен на рисунке следующего слайда, на котором оцифровка диаграмм соответствует точкам схемы. Выходной сигнал фильтра имеет желаемую форму, т.е. нулевой уровень боковых лепестков. Легко подсчитать, что энергетические потери в ФПБЛ ![]() (0,46 дБ).
(0,46 дБ).

