5.3.1. Дистанционное уравнение
5.3.2. Мощность принятого сигнала как функция частоты
5.3.1. Дистанционное уравнение
Основная задача бюджета канала — доказать, что система связи будет работать согласно плану; т.е. качество сообщений (достоверность передачи) будет удовлетворять заданным требованиям. Бюджет канала отслеживает "потери" и "прибыли" (усиление и ослабление) передаваемого сигнала от начала его формирования в передатчике до полного получения в приемнике. Вычисления показывают, чему равно отношение 
в приемнике и какой запас прочности существует. Процесс вычисления бюджета канала начинается с дистанционного уравнения, связывающего принятую мощность с расстоянием между передатчиком и приемником. Вывод этого уравнения дан ниже.
В системах радиосвязи несущая распространяется от передатчика посредством передающей антенны. Передающая антенна — это устройство, преобразовывающее электрические сигналы в электромагнитные поля. В приемнике принимающая антенна выполняет обратное преобразование; она превращает электромагнитные поля в электрические сигналы. Вывод уравнения, связывающего приемник и передатчик, обычно начинается с рассмотрения ненаправленного источника радиоизлучения, равномерно передающего в 4π стерадиан. На рис. 5.3 показан идеальный источник, называемый изотропным излучателем (isotropic radiator). Поскольку площадь поверхности сферы радиуса d равна 4πd, плотность мощности p(d) данной сферы с центром в источнике излучения связана с переданной мощностью Рt.
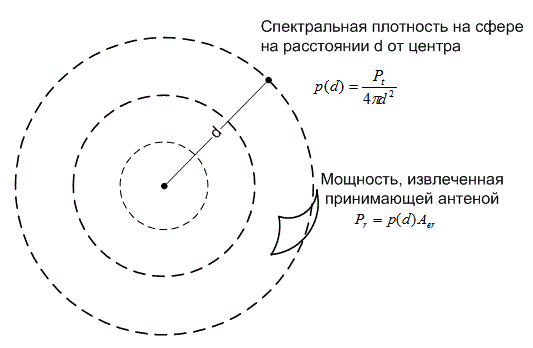
Рис. 5.3. Дистанционное уравнение. Выражение принятой мощности через расстояние
(5.1)
Мощность, извлеченную принимающей антенной, можно записать следующим образом.
(5.2)
Здесь параметр Аer — это сечение захвата (эффективная площадь) принимающей антенны, определяемое следующим образом.
(5.3)
Если рассматриваемая антенна является передающей, ее эффективная площадь обозначается как Аet. Если не указано, выполняет ли антенна принимающую или передающую функцию, эффективная площадь обозначается через Ае.
Эффективная площадь антенны Аe, и ее физическая площадь поверхности Арсвязаны коэффициентом эффективности η.
(5.4)
Это говорит о том, что не вся мощность падающего луча была извлечена; вследствие различных механизмов [3] происходят потери. Номинальное значение η для параболической антенны составляет 0,55, а для рупорной — 0,75.
Определим параметр антенны, который связывает выходную (или входную) мощность с мощностью изотропного излучателя и именуется коэффициентом направленного действия.
(5.5)
При отсутствии любых диссипативных потерь или потерь вследствие несогласованности импедансов коэффициент направленного действия антенны (в направлении максимальной интенсивности излучения) определяется из формулы (5.5). В то же время, если существует некоторая диссипация или несогласованность, коэффициент направленного действия антенны уменьшается на множитель, соответствующий объему потерь [4]. В данной главе мы будем предполагать, что диссипативные потери равны нулю, а импедансы согласованы идеально. Таким образом, формула (5.5) описывает максимальный коэффициент направленного действия антенны; как показано на рис. 5.4, его можно рассматривать как результат концентрации изотропного излучения в некоторой ограниченной области, меньшей 4я стерадиан. Теперь мы можем определить эффективную излученную мощность относительно изотропного излучателя (эффективная изотропно-излучаемая мощность — effective isotropic radiated power, EIRP) как произведение переданной мощности Рt и коэффициента усиления передающей антенны Gt.
EJRP = PtGt, (5.6)
Пример 5.1. Эффективная изотропно-излучаемая мощность
Покажите, что при надлежащем выборе антенн можно получить одинаковое значение EIRP как при использовании передатчика с Рt = 100 Вт, так и при использовании передатчика с Рt = 0,1Вт.
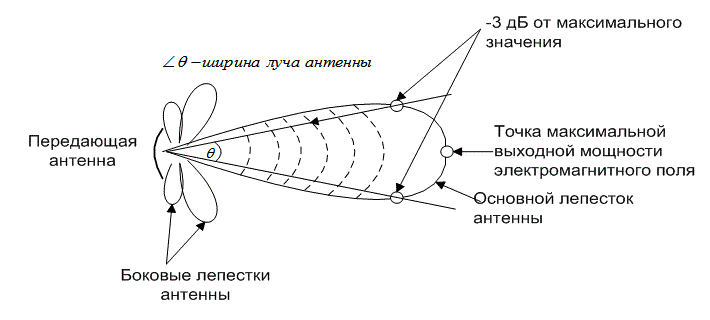
Рис. 5.4. Коэффициент направленного действия антенны — результат концентрации изотропного излучения
Решение
На рис. 5.5, а показан передатчик с Рt = 100 Вт, соединенный с изотропной антенной; значение EIRP = PtGt = 100 х 1 = 100 Вт. На рис. 5.5, б показан передатчик с Рt = 0,1 Вт, соединенный с антенной, имеющей Gt = 1000; EIRP=PtGt = 0,1 x 1000 = 100 Вт. Если измерители напряженности поля расположены так, как показано на рисунке, то измеряемая с их помощью эффективная мощность не будет отличаться.
а)
б)
Рис. 5.5. Два различных способа получения одинакового значения EIRP
5.3.1.1. Возвращаясь к дистанционному уравнению
Если антенна передатчика имеет некоторый коэффициент направленного действия, отличающийся от предоставляемого изотропной антенной, в уравнении (5.2) мы меняем Рt на EIRP, что дает следующее.
(5.7)
Связь между коэффициентом усиления антенны G и эффективной площадью Аe дается выражением [4].
(5.8)
Здесь λ — длина волны несущей. Длина волны λ и частота f связаны соотношением λ = c/f, где с — скорость света (
м/с). Теорема взаимности утверждает, что для данной антенны при данной длине волны коэффициенты направленного действия приема и передачи идентичны [4].
Зона обзора антенны является мерой телесного угла, в котором сконцентрирована большая часть мощности поля. Зона обзора — это мера анизотропных свойств антенны; она обратно пропорциональна усилению антенны, т.е. антеннам с большим коэффициентом усиления соответствует более узкая зона обзора. Часто зону обзора выражают не через телесный угол, а через плоский угол раствора антенны (beamwidth), измеряемый в радианах или градусах. На рис. 5.4 показана диаграмма направленности антенны и дана иллюстрация общего определения угла раствора антенны. Угол раствора — это угол, образованный точками, в которых максимальная мощность поля ослаблена на 3 дБ. Как угол раствора зависит от частоты сигнала и размера антенны? Из уравнения (5.8) можно видеть, что усиление антенны увеличивается с уменьшением длины волны (увеличением частоты); также усиление антенны увеличивается с увеличением эффективной площади. Увеличение усиления антенны равносильно фокусировке плотности потока энергии в меньшем угле раствора; следовательно, увеличение частоты сигнала или размера антенны приводит к сужению угла раствора.
Эффективную площадь изотропной антенны можно вычислить, положив в уравнении (5.8) G=1, что позволяет получить следующее выражение для Аe.
(5.9)
Затем для нахождения принятой мощности Рr, при изотропной принимающей антенне, подставляем уравнение (5.9) в уравнение (5.7), что дает следующее.
(5.10)
Здесь совокупность коэффициентов 
называется потерями в тракте (path loss) или потерями в свободном пространстве (free-space loss) и обозначается через Ls. Формула (5.10) показывает, что мощность, принятая изотропной антенной, равна эффективной переданной мощности, сниженной только за счет потерь в тракте связи. Если принимающая антенна не является изотропной, то после замены в уравнении (5.7) Аer выражением 
из уравнения (5.8) получаем более общую формулу.
(5.11)
Здесь Gr — коэффициент усиления принимающей антенны. Полученное уравнение (5.11) называется дистанционным.
5.3.2. Мощность принятого сигнала как функция частоты
Поскольку и передающую, и принимающую антенны можно выразить через усиление или площадь, Рr можно выразить четырьмя различными способами.
(5.12)
(5.13)
(5.14)
(5.15)
В этих выражениях Аer и Аet — эффективные площади принимающей и передающей антенн.
В уравнениях (5.12)-(5.15) зависимая переменная — это мощность принятого сигнала Рr, а независимые переменные — это такие параметры, как переданная мощность, коэффициент усиления антенны, площадь антенны, длина волны и расстояние между антеннами. Допустим, возник вопрос: как меняется принятая мощность при увеличении длины волны (или уменьшении частоты), при фиксированных остальных параметрах? Если рассматривать уравнения (5.12) и (5.14), то кажется, что Рr и длина волны вообще не связаны. Из уравнения (5.13) величина Рr вроде бы обратно пропорциональна квадрату длины волны, а из уравнения (5.15) она прямо пропорциональна квадрату длины волны. Нет ли здесь противоречия? Разумеется, нет; кажущаяся противоречивость уравнений (5.12)-(5.15) исчезает, если вернуться к формуле (5.8) и вспомнить, что коэффициент усиления антенны и ее площадь связаны через длину волны. Когда следует употреблять каждое из уравнений (5.12Н5.15) для определения зависимости Рr от длины волны? Представим уже сконструированную систему, т.е. антенны уже построены (зафиксированы Аet и Аer). В этом случае подходящим выбором для вычисления Рr является уравнение (5.13), сформулированное для антенн фиксированного размера. Из этого уравнения видим, что принятая мощность увеличивается при уменьшении длины волны.
Рассмотрим уравнение (5.12), где независимыми переменными являются Gt и Aer. Итак, желательно, чтобы Gt и Аer были фиксированными при вычислении зависимости Рr от длины волны. Как изменится усиление при передаче на фиксированное расстояние, если уменьшить независимую переменную λ? Gt увеличится (см. уравнение (5.8)). Но мы не хотим увеличения Gt — оно нужно нам фиксированным. Другими словами, чтобы обеспечить неизменность Gt, нам необходимо уменьшать размер передающей антенны при уменьшении длины волны. Рассуждая подобным образом, приходим к выводу, что уравнение (5.12) удобно использовать при фиксированном усилении передающей антенны (или растворе антенны) и при переменном параметре Аet. Подобным образом уравнение (5.14) используется при фиксированных Аet и Gr a уравнение (5.15) — при фиксированных коэффициентах усиления передающей и принимающей антенн (или растворах антенн).
На рис. 5.6 показано спутниковое приложение, где для обзора земной поверхности требуется луч со спутниковой антенны (раствор антенны равен порядка 17°). Поскольку коэффициент усиления спутниковой антенны Gt должен быть фиксированным, результирующая мощность Рr (см. уравнение (5.12)) не зависит от длины волны. Если передача ведется на определенной частоте 
, то изменение ее на f2, где 
, приведет к уменьшению обзора (поскольку при данной антенне увеличится Gt); таким образом, для поддержания требуемого обзора или раствора антенны размер этой антенны должен быть уменьшен. Итак, при увеличении несущей частоты антенны обзор земной поверхности уменьшается.
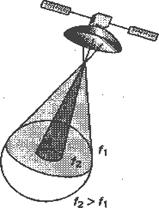
Рис. 5.6. Принятая мощность как функция частоты
5.3.3. Потери в тракте зависят от частоты
Из уравнения (5.10) можно видеть, что потери в тракте Ls зависят от длины волны (частоты). Довольно часто возникает вопрос: почему потери в тракте, подчиняющиеся простому геометрическому закону ослабления (ослабление обратно пропорционально квадрату расстояния), зависят от частоты? Ответ заключается в том, что потери в тракте, выраженные в уравнении (5.10), определены для изотропной принимающей антенны (Gr=1). Вообще, потери в тракте — это весьма удобный параметр; он представляет гипотетическую потерю мощности, которая произойдет, если принимающая антенна будет изотропной. Из рис. 5.3 и уравнения (5.1) видно (из чисто геометрических соображений), что плотность мощности p(d) — это функция расстояния, p(d) не является функцией частоты. В то же время, поскольку потери в тракте заданы для Gr= 1, когда мы находим некоторую мощность Рr с помощью изотропной антенны, результат описывается выражением (5.10). Снова акцентируем внимание на том, что Ls можно рассматривать как совокупность параметров, которой было присвоено неудачное имя потери в тракте. Название представляет чисто геометрический эффект и не акцентирует внимания на том, что Gr= 1. Пожалуй, лучшим названием было бы потери распространения при единичном усилении. В системах радиосвязи потери в тракте — это наибольший единичный источник ослабления мощности сигнала. В спутниковых системах потери в тракте для канала связи со спутником в полосе С (6 ГГц) обычно составляют порядка 200 дБ.
Пример 5.2. Проект антенны для измерения потерь в тракте
Предложите эксперимент для измерения потерь в тракте Ls при частотах f1 = 30 МГц и f2 = 60 МГц, если расстояние между передатчиком и приемником равно 100 км. В обоих случаях найдите эффективную площадь принимающей антенны и вычислите потери в тракте в децибелах.
Решение
Два канала измерения Ls для частот f1 и f 2 показаны на рис. 5.7. Для обоих приемников удельная мощность p(d) одинакова и равна следующему.
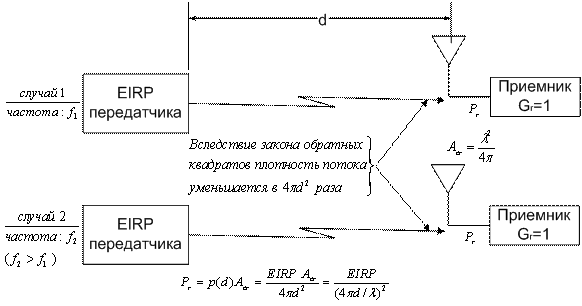
Рис. 5.7. Зависимость потерь в тракте от частоты. Предполагаемый эксперимент измерения потерь для двух различных частот
Это снижение удельной мощности происходит исключительно вследствие закона обратных квадратов. Действительная мощность, полученная каждым приемником, находится, как показано на рис. 5.7, посредством умножения плотности мощности p(d) в приемнике на эффективную площадь собирающей антенны Аer. Поскольку потери в тракте определены для Gr=1, эффективные площади Аer1 и Аer2 для частот f1 и f2 находятся с использованием уравнения (5.9).
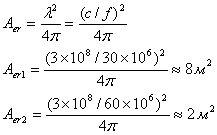
Далее для обоих случаев находим потери в тракте (в децибелах).
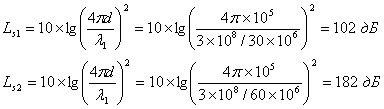
5.3.4. Мощность теплового шума
Тепловой шум вызывается тепловым движением электронов во всех проводящих элементах. Он создается в местах соединения антенны и приемника и в первых каскадах приемника. Спектральная плотность мощности шума постоянна для всех частот, вплоть до 1012 Гц, что определило название белый шум. Как показывалось в разделе 1.5.5, процесс теплового шума в приемниках системы связи моделируется как процесс аддитивного белого гауссового шума (additive white Gaussian noise — AWGN). Физическая модель [5, 61 теплового шума — это генератор шума со среднеквадратическим напряжением холостого хода, равным 
, где
k (константа Больцмана) = 
Дж/К или Вт/КГц
= -228,6 дБВт/КГц,
Т — температура, Кельвин
W — ширина полосы, Герц
и
— сопротивление, Ом
Максимальная мощность теплового шума N, которую можно подать с выхода генератора шума на вход усилителя, равна следующему.
(5.16)
Следовательно, максимальная номинальная односторонняя спектральная плотность мощности шума N0 (мощность шума на 1 Гц полосы) на выходе усилителя равна следующему.
(5.17)
Может показаться, что мощность шума должна зависеть от значения сопротивления — но это не так. Рассмотрим такой аргумент. Соединим электрически большое и малое сопротивление так, чтобы они формировали замкнутую пару и их физические температуры были одинаковы. Если бы мощность шума зависела от сопротивления, то наблюдался бы поток полезной мощности от большего сопротивления к меньшему; большее сопротивление охлаждалось бы, а меньшее — нагревалось. Но это противоречит нашему жизненному опыту, не говоря уже о втором начале термодинамики. Следовательно, мощность, поступающая от большего сопротивления к меньшему, должна равняться мощности, получаемой этим большим сопротивлением.
Как видно из уравнения (5.16), мощность, подаваемая источником теплового шума, зависит от температуры окружающей среды источника (шумовой температуры). Это позволяет ввести для источников шума полезное понятие эффективной шумовой температуры (причем источники не обязательно должны быть тепловыми по природе — галактика, атмосфера, интерферирующие сигналы), влияющей на работу принимающей антенны. Эффективная шумовая температура подобного источника шума определяется как температура гипотетического источника теплового шума, дающего эквивалентную паразитную мощность. Подробнее шумовая температура рассматривается в разделе 5.5.
Пример 5.3. Максимальная номинальная мощность шума
Используя генератор со среднеквадратическим напряжением, равным , покажите, что максимальная мощность шума, которую можно подать из такого источника на усилитель, равна 
.
Решение
Теорема из области теории электрических цепей утверждает, что максимальная мощность подается на нагрузку, если полное сопротивление (импеданс) нагрузки равно комплексно сопряженному импедансу генератора [7]. В нашем случае импеданс генератора — это чистое сопротивление, ; следовательно, условие передачи максимальной мощности удовлетворяется, если сопротивление усилителя равно 9t. Пример подобной схемы приведен на рис. 5.8. Источник теплового шума представлен электрически эквивалентной моделью, состоящей из бесшумного сопротивления, последовательно соединенного с идеальным генератором напряжения со среднеквадратическим напряжением 
. Теперь входное сопротивление усилителя равно . Напряжение шума, поступающего на вход усилителя, равно всего половине напряжения генератора, что следует из основных законов электрических схем. Таким образом, мощность шума, поданную на вход усилителя, можно выразить следующим образом.
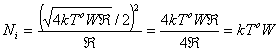
Рис. 5.8. Электрическая модель максимального теплового шума на входе усилителя