Профиль пролета. Его строят, используя топографическую карту местности. Профиль пролета представляет собой вертикальный разрез местности в плоскости, проходящей через линию АВ и центр Земли (рис. 9.1), где АВ — линия прямой видимости, соединяющая центры антенн. Для удобства профиль строят в прямоугольных координатах. Расстояния откладывают не по дуге окружности, соответствующей поверхности гладкой Земли, а по оси абсцисс, а высоты — не по радиусам Земли, а по оси ординат. Для того чтобы профиль в прямоугольных координатах соответствовал реальному, используют параболический масштаб. В этом масштабе все высоты отсчитываются не от оси x, а от линии условного нулевого уровня, имеющей вид параболы. Построение профиля начинают с расчета ординат этой параболы по соотношению

, (9.1)

где а₃=6370 км — геометрический радиус Земли; R₀ — протяженность пролета, k=R_i/R_o — относительная координата точки; R_i — расстояние от начала пролета до текущей точки. Достаточно рассчитать ординаты для точек 1...5, показанных на рис. 9.1,б. При вычерчивании берут разные масштабы по осям, так как высоты отсчитывают в метрах, а расстояния в километрах. Ординату начальной точки параболы (y=0, k=0) совмещают с уровнем моря (H=0), а абсциссу с R=0. В случае, когда средняя высота местности значительно выше уровня моря, высоту начальной точки параболы принимают на 10...20 м меньше самой низкой точки профиля (см. рис. 9.1,а), где при y=0 и k=0, h=120 м и R= 0. На профиль наносят высоты, указанные для данных точек местности на топографической карте, и местные объекты: лес, населенные пункты и др. Обязательно указывают водные поверхности: реки, водохранилища и т. п. Отмеченные высоты соединяют прямыми. Полученная ломаная линия и есть профиль пролета. На концах профиля откладывают высоты антенн h₁ и h₂ и проводят линию прямой видимости АВ. На профиле отмечают просвет Н — расстояние между линией прямой видимости и самой высокой точкой профиля. Для этой точки рассчитывают значение некоторого ориентировочного просвета:

(9.2)

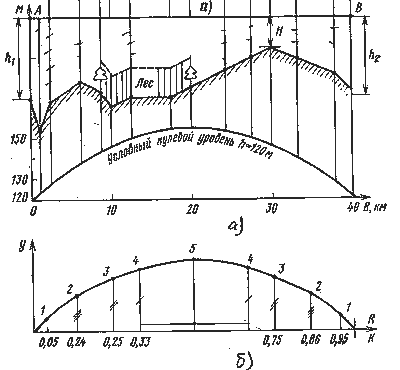
Рисунок 9.1. Профиль пролёта: а – к объяснению построения профиля; б – к выбору точек при построении линии условного нулевого уровня

Мощность сигнала на входе приемника при распространении в свободном пространстве. Множитель ослабления поля свободного пространства. По пути АВ распространяется прямая радиоволна. Земная поверхность практически не влияет на ее распространение, если на пролете H>H₀. При выполнении этого условия прямая радиоволна распространяется так же, как и в свободном пространстве.

Ненаправленный излучатель в свободном пространстве излучает одинаковую мощность во всех направлениях. Фронт электромагнитной волны на некотором расстоянии R от излучателя представляет собой сферу радиуса R. Мощность, проходящая через единицу поверхности этой сферы,

, (9.3)

где Р — мощность, подведенная к изотропному излучателю.

На пролете РРЛ устанавливают передающую и приемную антенны с коэффициентами усиления G_П и G_ПР соответственно. Антенны направлены друг к другу главными лепестками ДН. Для передающей антенны находим ЭИИМ при G = G_П. В таком случае плотность потока мощности в точке приема в соответствии с 9.3

(9.4)

Мощность сигнала на входе приемника при распространении в свободном пространстве , где - КПД приемного фидера, ему соответствуют потери а_Ф.ПР.

Подставив П₁ из (9.4) и положив G = G_ПР, запишем

(9.5)

При распространении в свободном пространстве суммарное ослабление мощности сигнала между выходом передатчика и входом приемника

Подставив (9.5), получаем:

(9.6)

Первый сомножитель этой формулы показывает ослабление сигнала между антеннами при распространении в свободном пространстве. Эта величина носит название основных потерь при распространении в свободном пространстве

(9.7)

Перейдя к уровням, записываем

, (9.8а)

(9.8б)

Уровень мощности сигнала на входе приемника ,

где р_П — уровень мощности передатчика. Значение р_С.ВХ0 получает ту же размерность, что и р_П.

В реальных условиях распространения мощность сигнала на входе приемника отлична от (9.5) из-за влияния земной поверхности и тропосферы. Учитывают это влияние с помощью множителя ослабления поля свободного пространства. Множитель ослабления показывает, во сколько раз напряженность поля в точке приема в реальных условиях (Е_Р) меньше, чем напряженность поля в той же точке при распространении в свободном пространстве (Е₀). Множитель ослабления

(9.9)

или

Поскольку состояние тропосферы непрерывно меняется, то и значение множителя ослабления меняется во времени.

При реальных условиях распространения мощность сигнала на входе приемника

Влияние земной поверхности. Сначала полагаем, что поверхность Земли — плоская, гладкая, однородная. В этом случае в точку приема приходят два луча: прямой АВ(1) и отраженный от земной поверхности АСВ(2) (рис. 9.2). Плоская поверхность дает только один отраженный луч. Координату точки отражения С определяют из условия равенства углов падения и отражения q . Просвет H определяют для этой точки. Между волнами 2 и 1 существует разность хода D r=ACB-AB, а следовательно, разность фаз в точке приема

(9.11)

где b — изменение фазы в точке С (фаза коэффициента отражения).

Вычислив АС, СВ и АВ из треугольников ADC, CBF и АbВ и приняв во внимание, что на реальных пролетах углы q малы, b =p и расстояния DC, CF и DF много больше, чем высоты антенн, получаем D r=2h₁h₂/R₀. Разность хода можно выразить через просвет. Учитывая, что на реальных трассах наклон линии АВ незначителен, полагаем h₁»h₂» H AB=R₀. При этих допущениях получаем

(9.12)

Сложив векторы сигналов 1 и 2, получаем реальную напряженность поля в точке приема (Е_Р на рис. 9.2,б). Выше отмечали, что условия распространения луча АВ такие же, как в свободном пространстве. Следовательно, амплитуда сигнала 1 равна Е₀ а сигнала 2 составляет Е₂=Е₀Ф, где Ф — модуль коэффициента отражения от земной поверхности.

Для гладкой земной поверхности Ф=1. Из треугольника 012 (рис. 9.2,б) получаем

,

Подставив это выражение в (9.9) и приняв во внимание (9.11),

при b =p получаем

(9.13)

В правой части (9.13) из-за изменения атмосферной рефракции D r меняется во времени. Формула (9.13) справедлива при распространении сигналов в пределах прямой видимости, когда H>H₀. Она получила название – интерференционная формула.

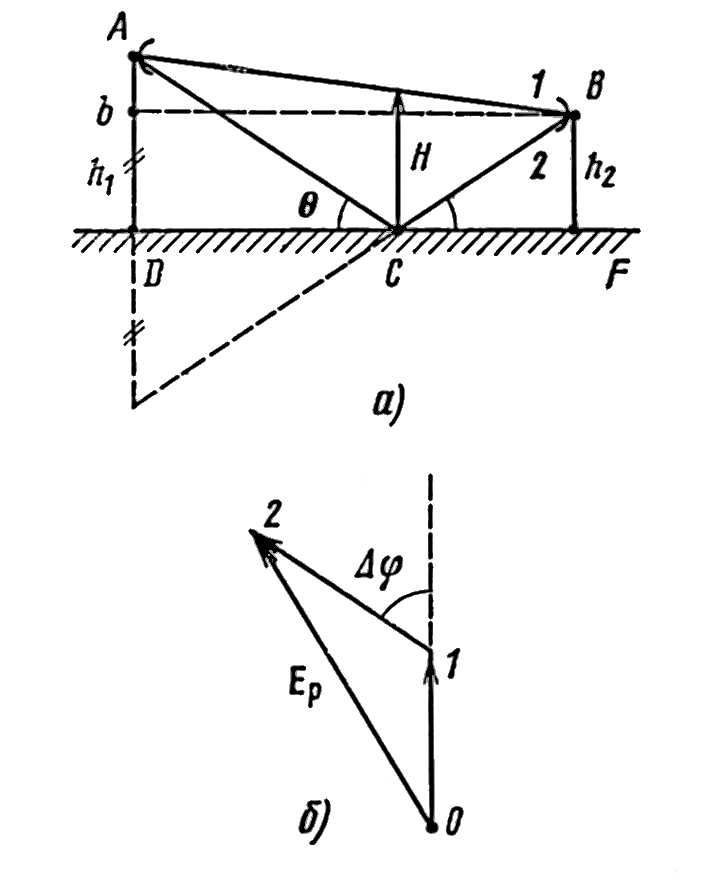
Рисунок 9.2. Ход лучей на пролёте при плоской, гладкой и однородной поверхности Земли (а) и векторная диаграмма на приёме (б)

Рассмотрим второй случай: земная поверхность – сферическая, гладкая, однородная. Теперь Ф<1 из-за явления расходимости радиоволн.

- коэффициент расходимости

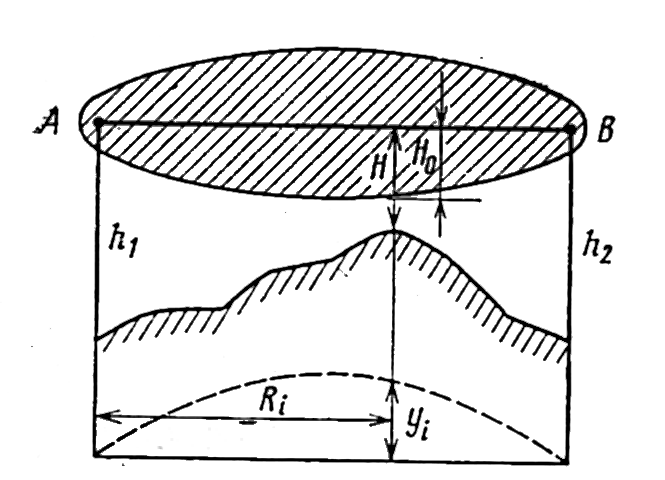
Рисунок 9.3. К пояснению условия прямой видимости на холмистой местности

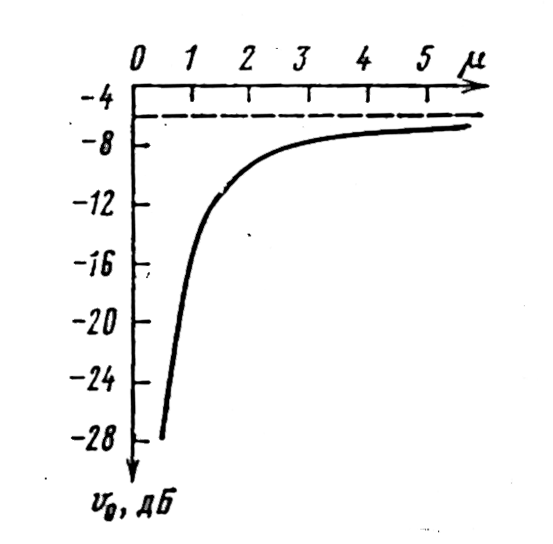
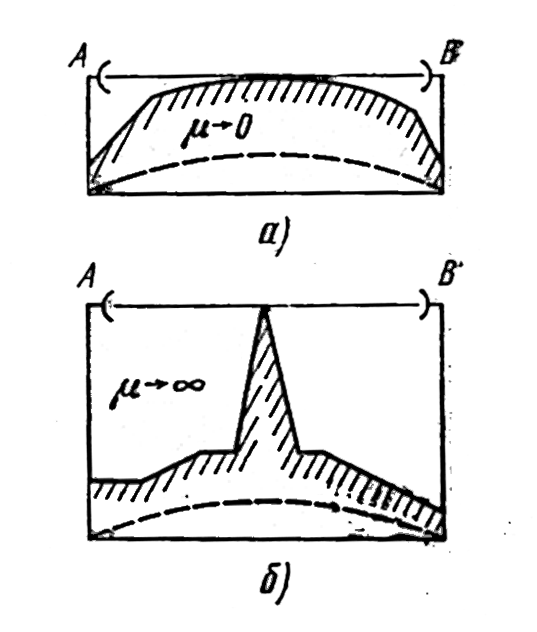
Рассмотрим реальный случай: земная поверхность — сферическая, неровная. Для этого случая лучевая трактовка распространения радиоволн неприменима, так как дает большую погрешность. Теперь нужно рассматривать область пространства, эффективно участвующую в распространении сигнала. Эта область представляет собой эллипсоид вращения, на большой оси которого лежит АВ (рис. 9.3). Сечение этого эллипсоида плоскостью профиля заштриховано, а сечение его в плоскости, перпендикулярной линии АВ представляет собой круг радиусом H₀, который называют первой полузоной Френеля. Если в самой высокой точке пролета H>H₀, то условия распространения прямой волны такие же, как и в свободном пространстве, и множитель ослабления определяют по интерференционной формуле. При HH₀препятствие экранирует прямую волну. Теперь множитель ослабления будет падать с уменьшением H, но он также будет зависеть от формы и размеров препятствия, которые принято оценивать с помощью параметра препятствия (л, характеризующего радиус кривизны препятствия. При H=0 трассу называют касательной. Поле в точке приема на ней создает дифрагирующая (огибающая препятствие) волна, для которой множитель ослабления v₀ определяют по рис. 9.8. Энергия волны, дифрагирующей вокруг сферического препятствия (рис. 9.5,а), для которого. m ® 0, почти на всем пути распространяется в непосредственной близости от Земли. Такое препятствие экранирует ее в большей степени, чем клиновидное препятствие (рис. 9.5,б), для которого m ® ¥ . Поэтому и значения v₀для этих двух видов препятствий будут значительно отличными друг от друга. Для реальных препятствий 0 < m < ¥ .

Влияние неровностей на отраженную волну состоит в том, что отражение может носить диффузный характер. В диапазоне СВЧ

Рисунок 9.4- К расчёту множителя ослабления на касательной трассе	Рисунок 9.5- Виды препятствий: сферические (а), клиновидное (б)

большинство поверхностей создает диффузное отражение (Ф<1). Зеркальное отражение имеет место только от совершенно гладких. площадок: аэродромов, гладких водных поверхностей и т. п.

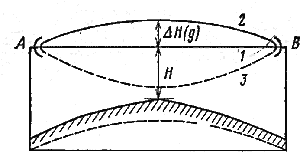
Влияние атмосферной рефракции. Для тропосферы можно определить относительную диэлектрическую проницаемость e , которая зависит от температуры и давления сухого воздуха, а также давления водяных паров. В хорошо перемешанной тропосфере содержание водяных паров и температура воздуха падают с высотой, поэтому и значение e уменьшается по высоте. Траектория электромагнитной волны в такой тропосфере будет искривлена (рис. 9.6, кривая 2). Прямая 1 на этом рисунке соответствует случаю распространения в свободном пространстве. Искривление траекторий волн, обусловленное неоднородным строением тропосферы, называется атмосферной рефракцией. Ее характеризуют градиентом диэлектрической проницаемости воздуха g=de /dh. В хорошо перемешанной тропосфере e падает с ростом высоты h, т. е. g<0, и траектория имеет выпуклую форму. Такую рефракцию называют положительной. С учетом рефракции просвет на пролете

H(g)=H+D H(g), (9.14)

где

(9.15) - приращение просвета

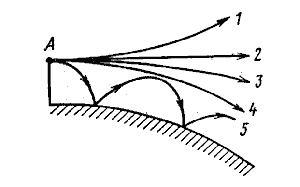
Рисунок 9.6. Траектории радиоволн в отсутствие рефракции (1), при положительной рефракции (2) и субрефракции (3)	Рисунок 9.7. Траектория радиоволн при различных видах атмосферной рефракции: 1 – при субрефракции; 2 – в отсутствие рефракции; 3 – стандартной; 4 – критической; 5 - сверхрефракции

Различают следующие виды рефракции (рис. 9.7). Рефракцию, соответствующую среднему состоянию тропосферы, называют стандартной, для нее g=-8× 10^-8 1/м. Это наиболее распространенный случай.

В вечерние, ночные и утренние часы летних месяцев в тропосфере иногда наблюдают температурные инверсии (рост температуры с высотой) и резкое уменьшение влажности. В этих условиях может возникать критическая рефракция, при которой траектория радиоволны концентрична земной поверхности, g=g_КР=-31.4(× )10^-8 1/м. При g<g_КР возникает сверхрефракция. Радиоволны в этом случае преломляются к поверхности Земли и отражаются от нее. Если в месте отоажения Ф=1, то возникает тропосферный волновод. Волна из пункта А в этом случае распространяется далеко за пределы прямой видимости и может создавать помехи другим РРС, использующим такие же частоты.

На участках РРЛ с низинами, где осенью или весной обычно имеют место приземные туманы, может возникнуть отрицательная рефракция или субрефракция, при этом g>0.Траектория радиоволны имеет вогнутый характер и просвет H(g)<H (см. рис. 9.4). Если на трассе имеется препятствие, то в этих условиях его экранирующее действие возрастает.

Расчет множителя ослабления в реальных условиях. Рефракционные замирания. Для реальных трасс определяют относительный просвет

p(g)=H(g)/H₀ (9.16)

В зависимости от значения p(g)различают трассы: открытые при p(g)>1 закрытые при p(g)<0 и полуоткрытые при 1>p(g)>0

На открытых трассах в точку приема приходят две волны: прямая и отраженная от поверхности Земли. Экранирующее действие препятствия не учитывают. Для расчета множителя ослабления применима интерференционная формула. Однако теперь разность хода лучей D r должна быть определена с учетом приращения просвета при рефракции. Поэтому полагаем H = H(g).

; p(g)1.

При изменении диэлектрической проницаемости воздуха множитель ослабления может принимать максимальные значения V_MAX=1+Ф, когда фазы прямой и отраженной волн на входе приемника совпадают, и минимальные V_MIN=1-Ф, при сложении этих волн в противофазе. Когда , где n=1, 2, 3, ...; V(t) = V_MIN и мощность сигнала в точке приема резко падает. Возникают замирания сигнала, которые носят название рефракционных замираний интерференционного типа. Это быстрые замирания. Их средняя длительность при глубине 35 ... 25 дБ составляет секунды — десятки секунд. Под глубиной понимают величину, численно равную |V_MIN|. Различные стволы РРЛ используют разные частоты (волны). Разность фаз D j между приходящими на вход приемника волнами зависит от длины волны. Поэтому замирания в ВЧ стволах происходят не одновременно. Эту особенность используют для борьбы с замираниями, а сами замирания характеризуют как частотно-зависимые или селективные. Если условия распространения на трассе таковы, что n=1, то говорят, что приемная антенна попала в первый интерференционный минимум, при п=2 — во второй и т.п.

При возрастании g просвет Н (g) на трассе уменьшается, и она может стать полуоткрытой и даже закрытой (g<0). Множитель ослабления падает. Возникают рефракционные замирания из-за экранирующего действия препятствия. Эти замирания сравнительно медленные (их длительность десятки минут — часы при глубине 35 ... 25 дБ) и наблюдаются одновременно во всех ВЧ стволах РРЛ.

Из-за случайных изменений g меняется угол прихода (выхода) радиоволн относительно главного направления приемной (передающей) антенны. Это явление приводит к колебаниям уровня сигнала на приеме. Такие колебания называют замираниями из-за влияния диаграмм направленности антенн. Это медленные замирания глубиной 10 ... 20 дБ. На практике такие замирания ощутимы при остронаправленных антеннах с коэффициентом усиления не ниже 45 дБ или 2q _0.5~0,9° ... 0,8°.

Влияние слоистых неоднородностей тропосферы. В тропосфере есть слои, диэлектрическая проницаемость которых отлична на небольшую величину D e от диэлектрической проницаемости окружающей тропосферы, например облака (рис. 9.8). Их называют; слоистыми неоднородностями. Если электромагнитная волна, отразившись от такой неоднородности, попадет на вход приемника, то векторная диаграмма принимаемых сигналов будет иметь вид, показанный на рис. 9.2,б. Только теперь волна 2 появилась из-за отражения от слоистой неоднородности тропосферы и ее амплитуда E₂=E₀Ф_ТР, где Ф_ТР — модуль коэффициента отражения от тропосферы. При выполнении условий Ф_ТР» 1 и D j = p , Е_Р=0, т. е. возникают глубокие замирания. Модуль коэффициента отражения зависит от соотношения между D e и углом скольжения к слою q , Ф_ТР=1 при D e q . Когда слоистая неоднородность расположена параллельно линии АВ, а точка отражения проектируется на середину трассы, из геометрических построений на пролете можно найти угол q и представить условие глубоких замираний в виде

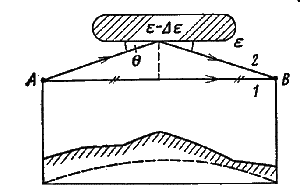
Рисунок 9.8. К пояснению отражения радиоволн от слоистых неоднородностей тропосферы

На реальной трассе высота и наклон слоя изменяется случайным образом, значит, амплитуда и фаза отраженной волны величины случайные. В момент, когда условие (9.16) выполняется, возникают глубокие интерференционные замирания из-за отражения от слоистых неоднородностей тропосферы. Это быстрые селективые замирания со средней длительностью доли секунд — секунды при глубине 35 ... 25 дБ. На трассах, проходящих вблизи водных массивов, где много слоистых неоднородностей, такие замирания наблюдают чаще, чем на сухопутных трассах.

Влияние гидрометеоров. Гидрометеоры в тропосфере (капли дождя, тумана, град, снег и т. п.) рассеивают энергию радиоволн, длина которых соизмерима с размерами гидрометеоров. Кроме того, происходит нерезонансное поглощение энергии в гидрометеорах. Эти эффекты проявляются при l <5 см, вызывая дополнительное ослабление сигнала на пролете. Обычно ослабление учитывают только для дождя. Множитель ослабления в дожде для волн с вертикальной поляризацией

, (9.17)

где g _Д — погонный коэффициент ослабления в дожде; R_Э — эффективная длина пролета, определенная в предположении, что на всем пролете идет дождь постоянной интенсивности, при которой значение v_Д рассчитанное по, совпадает по модулю с реальным ослаблением сигнала в дожде. Значение g _Д зависит от интенсивности осадков J. Слабый дождь — это осадки с J<5 мм/ч, при умеренном дожде J=5 ... 20 мм/ч, сильном — J=20 ... 40 мм/ч, для ливня J>40 мм/ч.

Волны с горизонтальной поляризацией испытывают большее ослабление из-за расплющивания капель дождя. Множитель ослабления для волн с горизонтальной поляризацией

v_Г=1.15v_Д

В литературе [1] можно найти зависимости v_Д(J) для различных диапазонов частот.