Предельными циклами называют ложные сигналы, которые возникают на выходе цепи, если на вход поступает сигнал в виде константы.
Предельные циклы появляются на выходе цепи вследствии ограничения разрядности кодовых слов на выходе умножителей.
Пример:
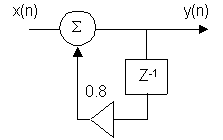
Определить форму и величину предельных циклов, если в последовательности x(n) в момент времени t=0 наступила пауза. При этом Y(–1) = 0.5, учитываем, что значение сигнала на выходе цепи ограничивается десятыми долями.
y(n) = x(n) + 0.8y(n – 1)
n=0 y(0) = 0 + 0.8·0.5 = 0.4
n=1 y(1) = 0 + 0.8·0.4 = 0.32 @ 0.3
n=2 y(2) = 0 + 0.8·0.3 = 0.21 @ 0.2
n=3 y(3) = 0 + 0.8·0.2 = 0.16 @ 0.2
n=4 y(4) = 0 + 0.8·0.2 = 0.16 @ 0.2
y(n) = {0.4; 0.3; 0.2; 0.2; 0.2…}
Если коэффициент (0.8) заменить на (–0.8), то на выходе получим:
y(n) = {–0.4; –0.3; –0.2; –0.2; –0.2…}
Предельный цикл становится знакопеременным.
Для цепи высокого порядка предельные циклы имеют сложную форму, которые трудно поддаются теоретическому анализу. При проектировании цифровых фильтров величина и форма предельных циклов выявляется результатом моделированием на ЭВМ.

