Сопоставление результатов измерения цвета возможно лишь при единой колориметрической системе, оперирующей вполне определенными, заранее согласованными основными цветами. Поэтому в целях устранения неопределенности измерения цвета в 1931 г. Международная комиссия по освещению (МКО) стандартизовала в качестве основных цветов – основных стимулов – три монохроматических излучения с длинами волн![]() R=700 нм,
R=700 нм, ![]() G=546,1 нм и
G=546,1 нм и ![]() B=435,8 нм. Выбранные основные цвета удобны тем, что два из них R и В близки к краям видимого спектра, а третий G — к его середине, поэтому каждый из них действует преимущественно на свой цветочувствительный аппарат. Кроме того, излучение
B=435,8 нм. Выбранные основные цвета удобны тем, что два из них R и В близки к краям видимого спектра, а третий G — к его середине, поэтому каждый из них действует преимущественно на свой цветочувствительный аппарат. Кроме того, излучение ![]() G и
G и ![]() B с большой интенсивностью испускается парами ртути, что упрощает проведение колориметрических измерений.
B с большой интенсивностью испускается парами ртути, что упрощает проведение колориметрических измерений.
Любой цвет в системе R, G, В определяется по аналогии с (2.1) выражением
f'F = r'R + g'G + b'B, (2.9)
где R,G,B – обозначения выбранных основных цветов, а r', g', b' – их количества, т.е. координаты цвета. Координаты цвета r', g', b' могут быть выражены в энергетических или световых единицах, но удобнее их выражать в количествах единичных цветов R, G, В. При этом символы R, G, В являются наименованием единиц измерения цвета. Абсолютные (количественные) значения единичных цветов колориметрической системы не устанавливают, нормируют лишь их соотношение. Его выбирают таким, чтобы при сложении единичных цветов в численно равных количествах получилось ощущение равноэнергетического белого цвета Е:
E = 1R + 10 + 1B. (2.10)
Такое соотношение основных цветов для белого цвета Е, как будет показано ниже, оказывается удобным при представлении цвета точкой в трехмерном пространстве или вектором. Из опыта смешения цветов известно, что для получения цветового ощущения белого от равноэнергетического излучения – источника типа Е необходимо к единице цвета R прибавить 4,5907 единицы цвета G и 0,0601 единицы цвета В. Тогда, если через LR, LG, LB обозначить относительные яркостные коэффициенты основных цветов, то количественное соотношение компонентов смеси можно записать как:
LR r'E : LG g'E : LB b'E = 1:4,5907:0,0601 (2.11)
где r'E, g'E, b'E – координаты белого цвета равноэнергетического излучения Е, которые в системе RGB будут:
![]() (2.12)
(2.12)
Координаты цвета r', g', b' любого сложного излучения могут быть определены, если известен спектральный состав этого излучения Р(![]() ):
):
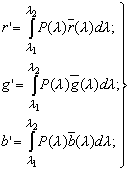 (2.13)
(2.13)
Величины ![]() представляют собой цветовые свойства среднего наблюдателя, фиксирующего достижения цветового равенства (2.9), которые были стандартизованы в 1931 г. МКО на основе экспериментальных результатов, полученных Райтом и Гилдом. Цветовые свойства наблюдателей были стандартизованы для монохроматического излучения мощностью 1 Вт во всем видимом диапазоне длин волн. В результате были получены удельные координаты или удельные цветовые коэффициенты, которыми называются коэффициенты цветового уравнения (2.9) необходимые для получения ощущения цвета, соответствующего монохроматическому излучению мощностью в 1 Вт. Графическая зависимость удельных координат длины волны или кривые смешения изображены на рисунке 2.4. Они связывают воздействующее на глаз излучение данного спектрального состава с результатом этого воздействия – ощущением цвета, выраженным в цветовых координатах r', g', b'.
представляют собой цветовые свойства среднего наблюдателя, фиксирующего достижения цветового равенства (2.9), которые были стандартизованы в 1931 г. МКО на основе экспериментальных результатов, полученных Райтом и Гилдом. Цветовые свойства наблюдателей были стандартизованы для монохроматического излучения мощностью 1 Вт во всем видимом диапазоне длин волн. В результате были получены удельные координаты или удельные цветовые коэффициенты, которыми называются коэффициенты цветового уравнения (2.9) необходимые для получения ощущения цвета, соответствующего монохроматическому излучению мощностью в 1 Вт. Графическая зависимость удельных координат длины волны или кривые смешения изображены на рисунке 2.4. Они связывают воздействующее на глаз излучение данного спектрального состава с результатом этого воздействия – ощущением цвета, выраженным в цветовых координатах r', g', b'.
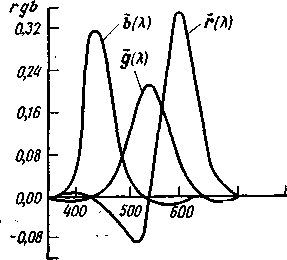
Рисунок 2.4. Удельные координаты цвета в системе RGB
Для равноэнергетического белого цвета и РЕλ = const и r'E=g'E=b'E, откуда
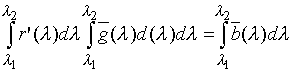 (2.14)
(2.14)
а следовательно, площади под кривыми ![]() равны.
равны.
Отрицательные участки ординат кривых смешения показывают, что в цветовом уравнении (2.9) величины r', g', b' для чистых спектральных цветов имеют отрицательные значения. Это подтверждает невозможность получения чистых спектральных цветов смешением основных реальных цветов RGB.
На рисунке 2.5 представлен конус реальных цветов – цветовое тело, построенное на векторах основных цветов колориметрической системы RGB. Плоскость Q пересекает координатные оси RGB в точках, соответствующих единичным количествам основных цветов, и, следовательно, является единичной плоскостью. Вектор равноэнергетического белого цвета Е равноудален от векторов основных цветов, чем достигается равномерность заполнения цветового пространства.
След пересечения плоскости Q с конической поверхностью цветового тела образует локус чистых спектральных цветов. Следы пересечения этой плоскости с координатными плоскостями образуют цветовой треугольник RGB. Любой точке в плоскости треугольника RGB соответствует вполне определенная цветность, координаты которой определяются путем деления модулей цвета r', g', b' на их сумму в соответствии с (2.5).
Для опорного равносигнального цвета Е координаты цветности
rE=gE=bE=1/3
Следовательно, точка белого цвета E является центром тяжести треугольника RGB и лежит на пересечении его медиан. Рассматривая положение цветового конуса в пространстве координат RGB, видим, что значительная часть цветового тела, содержащая векторы монохроматических зеленых, голубых, синих и фиолетовых цветов, выходит за пределы пирамиды OBGR, т.е. оказывается с внешней стороны плоскости GOB. Соответственно и след сечения цветового конуса плоскостью Q – спектральный локус выходит за пределы цветового треугольника RGB. Следовательно, чистые спектральные цвета не могут быть получены смешением основных цветов RGB и входящие в цветовые уравнения модули r', g', b' для этих цветов могут иметь отрицательные значения. Кривые смешения (рисунок 2.4) подтверждают это положение.
Колориметрическая система RGB удобна для проведения экспериментальных исследований, так как её основные цвета являются реальными, физически существующими цветами. Однако наличие в кривых смешения RGB (рисунок 2.4) положительных и отрицательных ветвей значительно затрудняет их реализацию при создании цветоизмерительных приборов – колориметров. Вторым недостатком системы RGB является необходимость расчета всех трех компонентов цвета при определении его яркости:
L = 683(LRR + LGG + LBB),
где R, G, В — координаты цвета; LR, LG, LB – яркостные коэффициенты основных цветов системы RGB. Поэтому в 1931 г. МКО была принята более удобная колориметрическая система нереальных цветов XYZ.
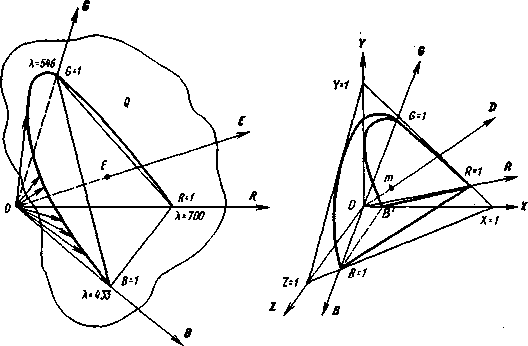
| Рисунок 2.5 Цветовое тело, построенное на векторах реальных цветов RGB | Рисунок 2.6 Цветовое пространство XYZ и получение диаграммы цветности МКО |

