5.1. Передача энергии по симметричной цепи с учётом потерь

5.2. Внутренняя индуктивность, емкость и сопротивление изоляции симметричной цепи

5.3. Вторичные параметры передачи симметричных цепей

5.4. Коаксиальные цепи. Электрические процессы в коаксиальных цепях

5.5. Параметры передачи коаксиальных цепей

5.6. Оптимальное соотношение диаметров проводников коаксиальной цепи

5.7. Свойства неоднородных линий

5.1. Передача энергии по симметричной цепи с учётом потерь

При передаче энергии по НС потери в проводнике определяются радиальной составляющей вектора Пойтинга, которую формирует составляющие и . Мощность потока энергия для цилиндрического проводника определяется

,

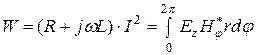откуда 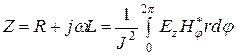, (5.1)

где L – внутренняя индуктивность проводника, а R - его активное сопротивление.

Анализируем гармонические колебания в квазистационарном режиме, среда не содержит сторонних токов, токи смещения отсутствуют, т.е. .

Для определения составляющих поля необходимо воспользоваться уравнениями Максвелла:

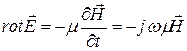; (5.2)

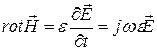. (5.3)

Применим операцию к (4.2):

. (5.4)

Для любого вектора выполняется тождество

, (5.5)

где - оператор Лапласа.

Решение уравнений Максвелла для цилиндрического проводника целесообразно проводить в цилиндрической системе координат. Тогда

.

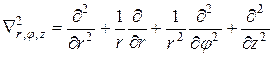Учитывая отсутствие в системе сторонних токов, а следовательно и свободных зарядов, и .

Тогда (5.4) с учётом (5.3) примет вид:

. (5.6)

Полученное уравнение называется волновым. Обычно волновое уравнение решается для продольных составляющих поля и , которые дают возможность определить все шесть составляющих электромагнитного поля.

Распределение продольных составляющих поля вдоль линии представляется как . Тогда волновое уравнение примет вид

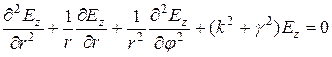, (5.7)

где - поперечное волновое число, для Т – волн , т.е. , т.к. анализируется процесс распространения в металле, обозначим - волновое число для металла. Уравнение (5.7) – это уравнение частных в производных с разделяющимися переменными, его решение для металла имеет вид:

, (5.8)

Это выражение описывает структуру поля в поперечном сечении системы. Первый сомножитель определяет распределение поля в радиальном направлении, второй в азимутальном.

где A, B, C, D – постоянные интегрирования, - коэффициент вихревых токов для металла, и - модифицированные функции Бесселя n–го порядка второго рода. Постоянные интегрирования определяются из граничных условий на границе раздела сред металл / диэлектрик.

Так как поле внутри проводника возрастает от центра к периферии, а функция с увеличением аргумента уменьшается, необходимо принять . В силу симметричного расположения проводников относительно горизонтальной оси, нечётная функция должна обращаться в нуль, т.е. . Учитывая наличие бесконечного числа составляющих поля, получим для проводников

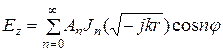. (5.9)

Составляющую магнитного поля определим как

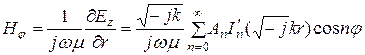. (5.10)

определяются из граничных условий и закона полного тока. Функции Бесселя второго рода это функции комплексной переменной, представляются в виде суммы действительной и мнимой составляющих.

(5.11)

и аргумент этих функции имеет вид

т. к. .

Таким образом, полученные выражения и после подстановки их в (6.1) и разделения этого выражения на действительную и мнимую части позволяют получить аналитические выражения для R и L:

. (5.12)

где I – ток в цепи.

Далее необходимо в (6.12) подставить (6.9) и (6.10) и (6.11), произвести соответствующие преобразования.

Дальнейшие преобразования являются достаточно громадно, окончательные выражения для активного сопротивления и внутренней индуктивности принимают вид

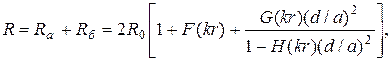(5.13)

, (5.14)

Внутренняя индуктивность симметричной цепи определяется выражением, Гн/км

где d – диаметр проводника, а – расстояние между ними (рис. 5.1), - сопротивление проводника по постоянному току. Функции I, F, H, G, Q определяются комбинациями функций Бесселя, их значения приведены в таблицах (см. приложение), , r– радиус проводника.

С учётом различных скруток в кабеле выражение для расчёта сопротивления симметричного кабеля имеет вид, Ом/км

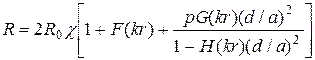. (5.15)

При парной скрутке , при звёздной – , при двойной парной - ; в зависимости от диаметра кабеля. На рис. 5.1 приведено распределение магнитного поля симметричной пары. Поля проводников а и б взаимодействуя между собой увеличивают сопротивление цепи.

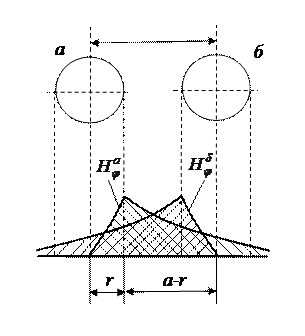
Рис. 5.1. Поле симметричной пары

Первое слагаемое в (5.15) определяет сопротивление цепи по постоянному току, второе – сопротивление вследствие поверхностного эффекта, а третье – сопротивление вследствие эффекта близости.

5.2. Внутренняя индуктивность, емкость и сопротивление изоляции симметричной цепи

В двухпроводной цепи распространяется ТЕМ-волна, т.е. структура поля в поперечном сечении эквивалентна структуре поля постоянного тока и постоянных зарядов, поэтому для определения внешней индуктивности и ёмкости можно воспользоваться известными соотношениями для статического режима (определение ёмкости С) и стационарного (определение индуктивности L) режима. Индуктивность определяет способность системы накапливать магнитную энергию.

Внешняя индуктивность определяется на длину линии в 1 км, используя соотношения

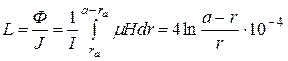, Гн/км , (5.17)

где Ф – магнитный поток, I – ток в системе.

Внешняя индуктивность не зависит от частоты, она определяется геометрией системы.

Общая индуктивность симметричной кабельной цепи,

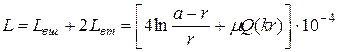. (5.18)

Ёмкость Си проводимость изоляции G связаны с процессами в диэлектрике. Под действием переменного электромагнитного поля в диэлектрике происходит переориентация диполей и поляризация диэлектрика. Ёмкость характеризует возможность системы проводников запасать энергию электрического поля, поляризацию диполей, величину токов смещения. Проводимость изоляции определяет величину потерь в диэлектрике на поляризацию диполей и характеризуется тангенсом угла диэлектрических потерь . Ёмкость определяется соотношением

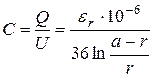, Ф/км, (4.19)

где Q – заряд в системе, U – разность потенциалов между проводниками. Ёмкость цепи не зависит от частоты.

Для определения проводимости изоляции воспользуемся частью схемы двухпроводной цепи, содержащей поперечные параметры (рис. 4.2).

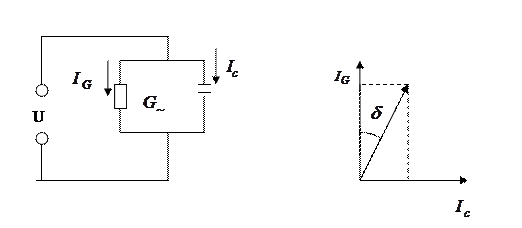
а) б)

Рис. 5.2 – Схема цепи с поперечными параметрами (а) и векторная диаграмма для этой цепи (б)

; ; ,

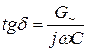откуда получаем

В общем случае, сопротивление изоляции содержит две составляющих

,

где – сопротивление изоляции постоянному току, т.е. . Обычно , поэтому .

Кабели связи, как правило, имеют сложную комбинированную изоляцию, в расчетах принимаются эквивалентные значения и , учитывающие долю диэлектрика в общем объёме изоляции. Следует отметить, что с ростом частоты увеличивается, но в диапазоне частот, в котором используется та или иная цель это величина практически постоянная.

5.3. Вторичные параметры передачи симметричных цепей

Вторичные параметры передачи следует рассчитывать по формулам (3.11, 3.14, 3.15, 3.16). Вторичные параметры с некоторыми допущениями можно выразить непосредственно через геометрические параметры цепей и параметры изоляционных материалов . Волновое сопротивление определяется

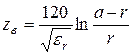, . (5.20)

Затухание рассчитывается по формуле:

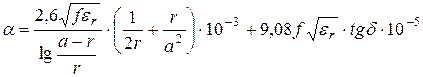, . (5.21)

Коэффициент фазы и скорость распространения определяются

или , ;

, ,

где – скорость света в свободном пространстве, .

Для симметричных цепей, в которых (воздушные линии связи, ленточные кабели), волновое сопротивление и затухание рассчитывается по формулам:

;

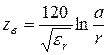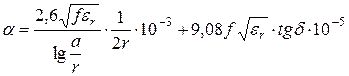. (5.22)

Первое слагаемое в (5.21) и (5.22) определяет потери в металлах, а второе – потери в диэлектрике. Потери в диэлектрике значительно меньше, чем потери в металле. С ростом частоты оба вида потерь возрастают – потери в металле пропорционально , а в диэлектрике – пропорционально частоте.

Вопросы для самоконтроля

1. Объясните методику определения сопротивления и внутренней индуктивности проводника.

2. Какие слагаемые в 5.13 определяют сопротивление постоянному току; сопротивление, вызванное поверхностным эффектом; сопротивление, вызванное эффектом действия окружающих масс?

3. Дайте определение внутренней и внешней индуктивности цепи.

4. Какие процессы происходят в диэлектрике НС?

5. Поясните векторную диаграмму на рис 5.2 б.

Письменные задания

1. Приведите зависимость первичных параметров передачи от частоты.

2. Изобразите поля симметричной цепи, воздушной линии связи, ленточного кабеля (2 проводника). Поясните, как распределение полей влияет на параметры и .

3. Получите расчётные соотношения для внешней индуктивности и ёмкости симметричной цепи.

4. Рассчитать сопротивление ленточного кабеля с медными проводниками, если диаметр проводников мм, а расстояние между ними мм на частоте 300 кГц.

5. Рассчитать первичные параметры передачи симметричной витой пары, если диаметр проводников мм, изоляция сплошная полиэтиленовая, толщина изоляции мм, частота кГц.

6. По результатам задачи 5 рассчитать вторичные параметры передачи.

7. Привести графики зависимостей вторичных параметров передачи симметричной цепи от частоты.

8. Пользуясь (3.11) определить пределы изменения в зависимости от частоты, сделать вывод.

5.4. Коаксиальные цепи. Электрические процессы в коаксиальных цепях

Основой коаксиального кабеля является коаксиальная пара. Коаксиальная пара - закрытая система, распространение поля в этой НС в радиальном направлении ограниченно и полностью сосредоточено в пространстве между проводниками (рис 4.3).

Рисунок 5.3. Магнитное поле коаксиальной цепи

Особенности распространения электромагнитной энергии по коаксиальной цепи обуславливают возможность передачи широкого спектра частот. Взаимодействие электромагнитных полей внешнего и внутреннего проводников коаксиальной пары таково, что поле за пределами проводника практически отсутствует.

Токи в проводниках и равны по величине, но противоположны по направлению. Следовательно, результирующее магнитное поле вне коаксиальной пары равно нулю:

.

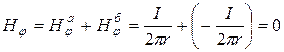Действие поверхностного эффекта и эффекта самоэкранирования в коаксиальной цепи приводит к эффекту самоэкранирования, который иллюстрируется рис. 5.4.

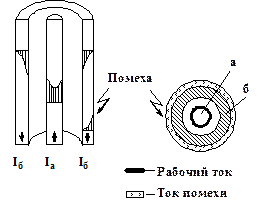
Рисунок 5.4. Эффект самоэкранирования в коаксиальной паре

Сущность эффекта самоэкранирования состоит в том, что рабочие токи сосредоточены на внутренней поверхности наружного проводника, т.е. коаксиальная цепь не создаёт помех соседним цепям. Токи помех, индуцированные внешними помехами, сосредоточены на внешней стороне внешнего проводника, т.е. они не индуцируют поле внутри коаксиальной пары. Эффект самоэкранирования объясняет незначительные взаимные влияния в коаксиальных цепях. С ростом частоты эффект самоэкранирования возрастает, а взаимные влияния уменьшаются, поэтому коаксиальные кабели используются на высоких частотах.

Разновидностью коаксиальных кабелей являются радиочастотные кабели, которые широко применяются в локальных сетях. Эффект самоэкранирования позволяет выполнять внешний проводник в виде оплетки, а не сплошным. Эти кабели используются на частотах до МГц, они обладают высокой помехозащищенностью, однако на высоких частотах имеют большое затухание.

В коаксиальной цепи распространяется ТЕМ–волна. Электрическое поле имеет составляющие и . Радиальная составляющая обуславливает наличие тока смещения в диэлектрике , продольная составляющая тока проводника. Кроме этих составляющих существует тангенциальная составляющая магнитного поля , которую порождает протекающий вдоль проводников ток проводимости .

5.5. Параметры передачи коаксиальных цепей

Методика определения первичных параметров передачи коаксиальной цепи такая же как и для симметричных цепей. Для частот свыше кГц (что практически всегда выполнимо для КК) используются следующие расчётные формулы. Сопротивление цепи для медных проводников определяется

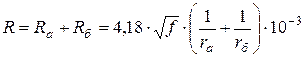, , (5.23)

где – диаметр внутреннего проводника, – внутренний диаметр внешнего проводника, мм., f – частота, Гц.

Внутренняя индуктивность для медных проводников:

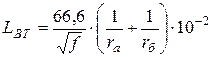, . (5.24)

Внешняя индуктивность определяется поперечными размерами цепи и для медных проводников рассчитывается по формуле

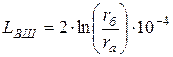, . (5.25)

Следует отметить, что .

Для алюминиевых проводников (4.23) и (4.24) имеют вид:

;

.

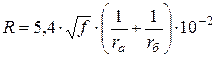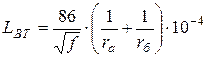Емкость цепи определяется

, .

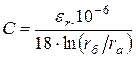Проводимость изоляции равна , См/км. В коаксиальных цепях . Вторичные параметры передачи рассчитываются по формулам:

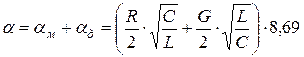дБ/км

; ; ,

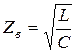где – затухание вследствие потерь в металле, – затухания вследствие потерь в диэлектрике.

Однако вторичные параметры передачи коаксиальных кабелей целесообразно выражать непосредственно через поперечные размеры коаксиальной пары ( и ) и параметры изоляции ( и ). Коэффициент затухания кабелей с медными проводниками определяется, дБ/км

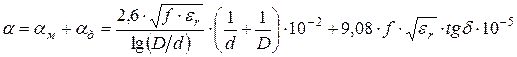. (5.26)

В некоторых типах коаксиальных кабелей внешний проводник часто выполняется из алюминия, при этом затухание кабеля возрастает незначительно. Это подвесные коаксиальные кабели, кабели для распределительных сетей кабельного телевидения. В радиочастотных кабелях наружный проводник часто выполняется из алюминиевой проволочной оплётки.

Как следует из (5.26) потери в металле пропорциональны , а потери в диэлектрике пропорциональны и растут значительно быстрее, чем потери в металле в области высоких частот.

Коэффициент фазы определяется формулой

или , рад/км.

Скорость распространения электромагнитной энергии , для коаксиальной пары

, .

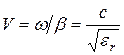Коэффициент фазы линейно возрастает с увеличением частоты. Это обуславливает постоянство скорости распространения энергии по коаксиальному кабелю в широком спектре частот. Такое постоянство необходимо при передачи цифровых сигналов. Скорость передачи уменьшается с увеличением диэлектрической проницаемости. В коаксиальных кабелях скорость передачи электромагнитной энергии приближается к скорости света в свободном пространстве.

Волновое сопротивление ( ) коаксиальной пары для высоких частот определяется выражением:

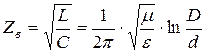(5.27)

или ,

где – волновое сопротивление диэлектрика.

Учитывая, что и , где Гн/м, Ф/м, получим

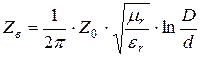, (5.28)

где Ом – волновое сопротивление свободного пространства. Для среды с получим

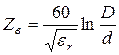. (5.29)

5.6. Оптимальное соотношение диаметров проводников коаксиальной цепи

Оптимальная конструкция коаксиальной пары предполагает при минимальных затратах материалов получить минимально возможные потери энергии.

Анализируя выражения для определения потерь в металле на высоких частотах (5.26), можно сделать вывод, что при определённом соотношении диаметров проводников коаксиальной пары, коэффициент затухания принимает минимальное значение.

Выразив через х продифференцировав первое слагаемое (5.26) по и приравняв производную , получим условие минимума функции

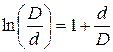(5.30)

Таким образом, минимальное затухание коаксиальной цепи обеспечится отношением . Это соотношение справедливо для кабелей с одинаковыми (медными) проводниками. Характер изменения затухания от соотношения диаметров проводников приведён на рис. 5.5.

Рисунок 5.5. Характер изменения затухания коаксиальной цепи с медными проводниками в зависимости от соотношения диаметров проводников

Так как волновое сопротивление коаксиального кабеля строго нормировано, на практике отношение несколько отличается от оптимального. Волновое сопротивление коаксиальной цепи существенно зависит от величины диэлектрической проницаемости. Для достижения нормированной величины Ом, при необходима изоляция с малым содержанием диэлектрика . При увеличении конструкция коаксиальной пары не является оптимальной, так при .

Если по кабелю необходимо обеспечить передачу большой мощности, то . Если же по кабелю необходимо передать максимальное напряжение, обеспечить максимальную электрическую прочность, то .

Для кабелей связи необходимо обеспечить минимальные потери энергии . Условие передачи максимальной мощности или достижение максимальной электрической прочности необходимо – в фидерах электро питании.

Вопросы и задания для самоконтроля

1. Какие особенности распространения энергии в коаксиальной цепи?

2. Какие составляющие поля существуют в коаксиальной цепи?

3. Объясните сущность эффекта самоэкранирования в коаксиальной цепи.

4. Как используется эффект самоэкранирования в коаксиальных кабелях различного назначения?

5. Объясните связь между составляющими поля и токами в коаксиальной цепи.

6. Объясните, почему коаксиальные кабели используются в области высоких частот.

7. Какими процессами определяется затухания в металле и затухание в диэлектрике?

8. Объясните смысл коэффициента фазы.

9. Как постоянная фазы и скорость распространения влияют на распространение цифровых сигналов?

10. Чем определяется волновое сопротивление КЦ на высоких частотах?

11. Каким конструктивным параметром определяется затухание коаксиального кабеля?

12. Какими параметрами диэлектрика определяется волновое сопротивление КК?

13. Какие свойства КП определяют различные соотношения её диаметров?

Письменные задания

1. Приведите структуру электромагнитного поля коаксиальной пары.

2. Приведите графики зависимостей первичных и вторичных параметров передачи от частоты.

3. Определите параметры передачи кабеля на частоте МГц, если , проводники алюминиевые, изоляция полиэтиленовая шайбовая.

4. Рассчитать зависимость затухания КК в зависимости от соотношения диаметров на частоте МГц, изоляция полиэтиленовая пористая мм. Интервал изменения D/d принять от 3 до 4,2 с шагом 0,2.

5. Коаксиальный кабель для локальной вычислительной сети имеет волновое сопротивление Ом. Определить соотношение диаметров проводников для различных значений диэлектрической проницаемости. Приделы изменения от до , с шагом . При каком значении затухание будет минимальным, максимальным. Определить эти затухания, если тактовая частота в сети МГц, мм.

6. Какое минимальное затухание может быть получено в кабеле для локальной сети со сплошной полиэтиленовой изоляцией на частоте МГц, если мм? Определить волновое сопротивление этого кабеля.

7. В какой из коаксиальных пар будет больше затухание: с или ? Объяснить ответ.

5.7. Свойства неоднородных линий

Проведённый выше анализ процессов и явлений в симметричных и коаксиальных цепях предполагал однородность линии. Однородная линия имеет постоянные электрические характеристики на всём протяжении, она нагружена на концах сопротивлениями, равными волновому . В этом случае отраженных электромагнитных волн нет и вся передаваемая энергия полностью поглощается приёмником, электрические процессы в линии точно описываются уравнениями (3.1, 3.2), а затухание линии определяется её собственным затуханием.

При изготовлении кабелей вследствие не совершенства технологии возникают различные дефекты: деформации изоляции, проводников, отклонения диаметров проводников и толщины изоляции от номинальных значений, эллиптичность проводников в коаксиальной паре, их несоосность и др. Вследствие этого кабель становится неоднородным по длине, изменяются его параметры, линия становится неоднородной. Однородность линии определяется постоянством волнового сопротивления по длине линии. Мерой неоднородности линии является коэффициент отражения p в месте сосредоточенной неоднородности (рис. 5.6).

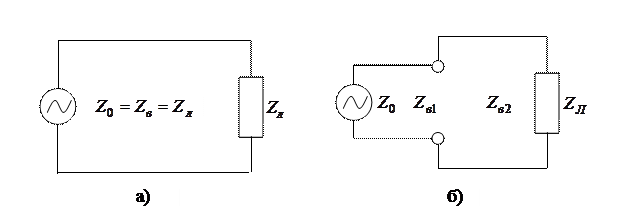
Рисунок 5.6. Схема однородной (а) и неоднородной (б) линии

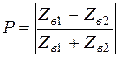. (5.31)

В неоднородной линии появляются отраженные волны, которые искажают характеристику собственного волнового сопротивления линии. Теперь линия характеризуется входным сопротивлением, характер которого приведен на рис. 5.7.

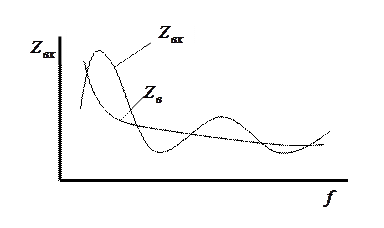
Рисунок 5.7. Частотная зависимость входного сопротивления цепи

Изменение входного сопротивления цепи на её концах приводит к несогласованности на концах линии и к появлению концевых отражений с коэффициентом отражения

,

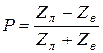где - входное сопротивление линии.

Дальность связи по неоднородной линии будет определяться не собственным затуханием линии , а рабочем затуханием

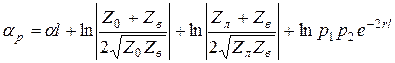, (5.32)

где и – коэффициенты отражения на стыках “генератор–кабель” и “приёмник–кабель”.

; .

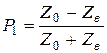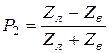Рабочее затухание - более общий параметр, т.к. кроме собственного затухания кабеля , учитывает также влияние несогласованности на стыках кабеля с нагрузкой.

В линиях неоднородных по длине различают внутренние неоднородности - в пределах строительной длины кабеля, и стыковые – обусловленные разбросом конструктивных, а следовательно, и электрических параметров.

Стыковые неоднородности, как правило, превышает внутренние неоднородности в кабеле сказываются, главным образом, на волновом сопротивлении кабеля, величина которого в месте сосредоточенной неоднородности отличается от номинальной.

Реальный кабель является неоднородной цепью. Электромагнитная волна, распространяясь по такой цепи и встречая на своём пути неоднородность, частично отражается от неё и возвращается к началу линии. При наличии нескольких неоднородных участков при распространении волны возникают многократные частичные отражения, что вызывает увеличение рабочего затухания и искажения характеристик цепи.

Неоднородности в кабеле приводят к появлению в цепи двух дополнительных потоков энергии: обратного (встречного), движущегося к началу цепи (генератору), и попутного, совпадающего с основным потоком. Схема образования встречных и попутных потоков представлена на рис. 5.2.

Рисунок 5.8. Схема образования встречного и попутного потоков

Попутный поток особенно проявляется на длинных линиях. Попутный поток искажает форму передаваемого сигнала, создаёт помехи. Появление попутного потока отрицательно влияет на передачу телевизионных сигналов, т. к. в этом случае нарушаются фазовые соотношение в структуре ТВ сигнала.

Величина попутного потока не должна превышать 1% основного. В аналоговых системах передачи попутный лимитируется на участке ОП1 – ОП2 линии, а в цифровых – на длине регенерационного участка.

Для повышения однородности электрических характеристик линии производится группирование строительных длин кабеля. При этом строительные длины располагают так, чтобы величины их волновых сопротивлений нарастали от начала регенерационного (усилительного) участка к его середине. На концах линии прокладываются кабели с номинальным волновым сопротивлением.

Вопросы для самоконтроля

1. Дайте определение однородной и неоднородной линии.

2. Чем характеризуется степень однородности линии?

3. Какие факторы приводят к неоднородности линии?

4. Дайте определение рабочего затухания.

5. Объясните смысл всех слагаемых в 5.1.

6. Как образуются встречный и попутный потоки?

7. Как влияют встречный и попутный потоки на передачу различных сигналов?

8. Какие неоднородности существуют в кабелях?

9. Какие меры применяются для повышения однородности линии?

Письменные задания

1. Определить рабочее затухание линии длиной 10 км, если затухание кабеля составляет 2 дБ/км, если волновое сопротивление кабеля Ом, Ом, Ом.

2. Мощность генератора в начале линии Вт, длина линии км, её километрическое затухание составляет дБ/км. Определить мощность обратного потока в начале линии, если Ом, а Ом.

3. Определить допустимое отклонение волнового сопротивления от номинального ( Ом), чтобы коэффициент отражения не превышал 0.02.

4. Предложить вариант группирования строительных длин кабеля с волновыми сопротивлениями: Ом, Ом, Ом, Ом, Ом.