12.1. Понятие объемного резонатора
12.2. Условие резонанса о объемных резонаторах
12.3. Основные типы объемных резонаторов
12.4. Собственная добротность объемных резонаторов
12.4.1. Нагруженная и внешняя добротности объемных резонаторов
12.1. Понятие объемного резонатора
Кратко вспомним, что изучили.
- Плоские волны в безграничном пространстве
-
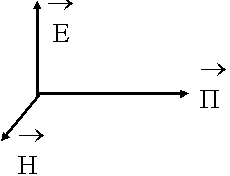
Граничные условия
-
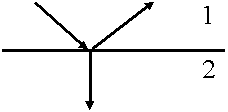
Волновод
Что же будет, если волну вообще загнать в замкнутое пространство?
Переходим к изучению волновых процессов, ограниченных замкнутой металлической полостью, называемую объемным резонатором.
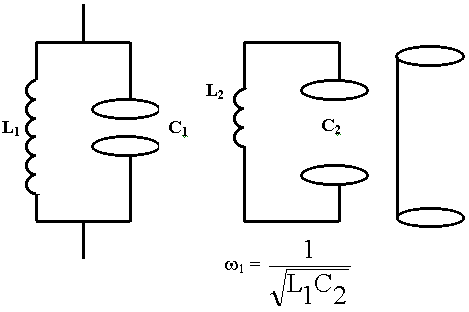
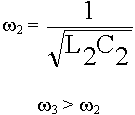
Уменьшаем L и C, в таком контуре добротность крайне низка, контур отдает свою энергию в окружающее пространство.
Что необходимо сделать для повышения добротности этого контура?
Попробуем вот так.
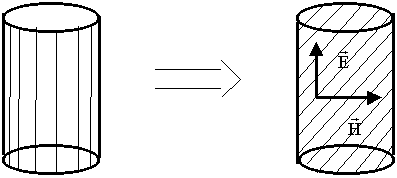
Излучение будет уменьшаться. В конце концов мы перейдем к замкнутой металлической полости. Это есть объемный резонатор.
На резонансной частоте происходит эффективный обмен энергиями электрического и магнитного полей.
А где найти конденсатор и катушку в этой коробке?
В каждой точке резонатора имеются электрические и магнитные поля и обмен между ними происходит в каждой точке.
Добротность собственная объемного резонатора оказалась много больше, чем у колебательного контура.
Q0 конт = 100 ¸ 300
Q0 объем.рез = 10000 ¸ 50000
Объемный резонатор в радиорелейной аппаратуре выполняет функцию колебательного контура - высокодобротного элемента.
12.2. Условие резонанса в объемном резонаторе
Это условие справедливо для случая, когда резонатор выполнен из отрезков
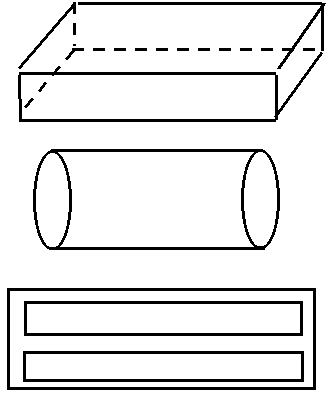
Установим связь между геометрическими размерами и резонансной частотой. Пусть имеется некоторая произвольная линия передачи с вектором магнитной волны.
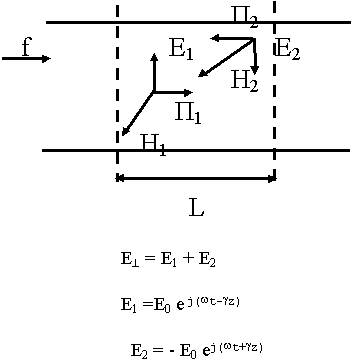
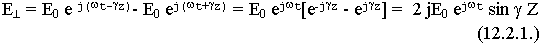
На торцевых поверхностях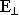 
= 0 при Z = 0 ; Z = L
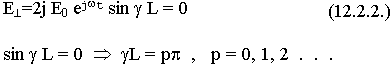
р - количество вариаций поля по длине резонатора.
Для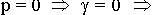 
в резонаторе поле отсутствует такая структура для Ez 
0, распространяется волна Е типа.
Для того, чтобы выполнялись граничные условия, L должна быть строго определенной.
= 
; = 
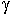длина волны в волноводе.
= 
L = p (
)
Lрез = p () (12.2.3.)
Для любых линий передачи:
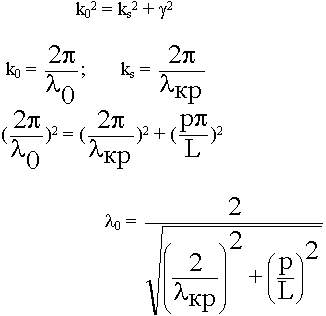
0 - резонансная длина волны:
fрез = 
(12.2.4.)
12.3. Основные типы объемных резонаторов
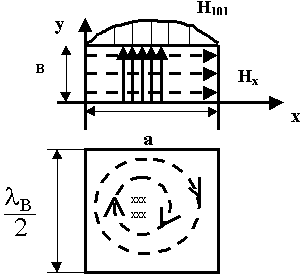
12.3.1. Прямоугольный резонатор
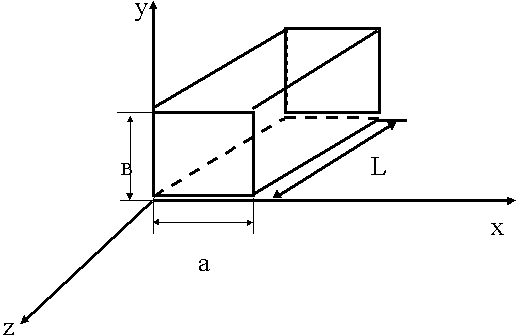
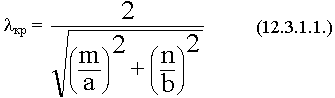
Для волн типа Н индексы m или n могут обращаться в 0. Для Е волн индексы m и n 0.
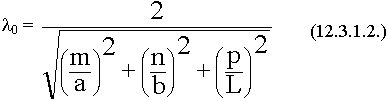
Индексам m и n соответствует своя структура поля. Введем обозначения Нmnp и Еmnp, р - показывает число полуволн укладывающихся вдоль длины резонатора.
m,n - число полуволн, укладывающихся вдоль ширины и высоты резонатора соответственно.
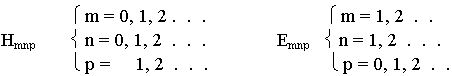
Для каждого типа волны - своя резонансная частота. Для получения минимальной резонансной частоты fрез надо использовать колебания с минимальными значениями m, n, p.
12.3.2. Цилиндрический резонатор
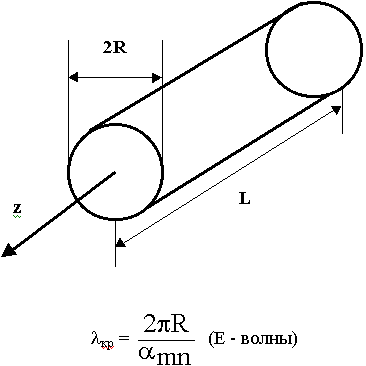
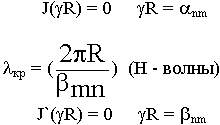
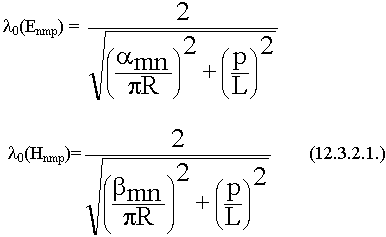
Основные колебания Н111 и Е010
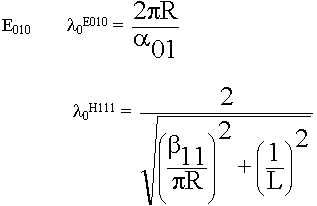
Может оказаться, что колебания имеют одну и туже резонансную частоту, это называется вырождением колебаний.
0E010 = 0H111
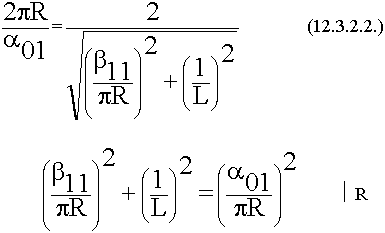
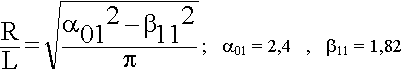
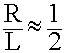
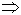когда D 
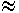L, то наблюдается вырождение, если D > L, то 
> 
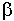
резЕ010 < резН111. Это означает, что Е010 - основное колебание. Если D < L, то < 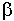, резЕ010 > резН111 Н111 - основное колебание.
n - число вариаций поля по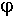 
вдоль азимута.
m - число вариаций по радиусу, порядковый номер функции Бесселя.
р - число вариаций поля по длине.
12.4. Собственная добротность ОР
В ОР за счет энергии внешнего источника (генератора) происходит накопление электромагнитной энергии. Наряду с накоплением энергии в ОР происходят процессы расхода энергии.
- На разогрев стенок резонатора - за счет преобразования поверхностных токов в тепловую энергию.
- Часть энергии расходуется из-за неидеальности резонатора (диэлектрические потери).
- Если в стенках резонатора имеются щели, то энергия выходит через них (излучение).
Собственная добротность - это отношение накопленной в резонаторе энергии к энергии рассеиваемой этим резонатором за 1 период:
Q0 = 2
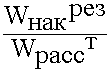(12.4.1.)
Выясним, от каких факторов зависит собственная добротность резонатора. Вся энергия заключена либо в электрическом, либо в магнитном поле.
Wmax Emax H = 0
Wmax Hmax E = 0
На резонансной частоте:
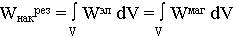
Найдем Wнакр и Wтрасс.рез:
Из теоремы Пойнтинга
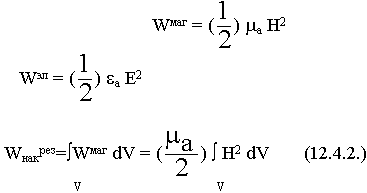
Энергия накопленная пропорциональна объему (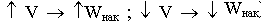 
)
Потери энергии :
- Потери за счет токов.
- Потери в среде, заполняющей объемный резонатор (диэлектрические потери).
- Потери на излучение, если есть щели, трещины.
Учтем только потери за счет поверхностных токов в стенках резонатора:
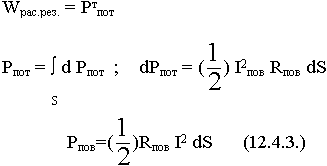
Поверхностные токи определяются магнитным полем:
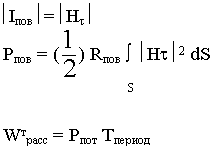
Получаем:
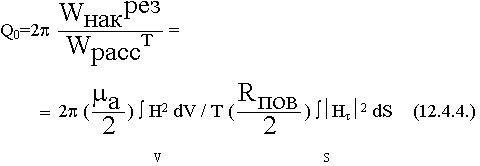
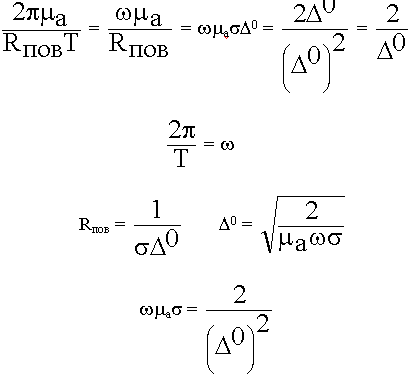
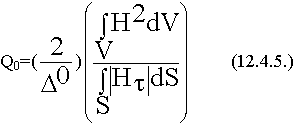
Выводы:
- Cобственная Q0 зависит от свойств материала, т.е. зависит от проводимости, чем больше проводимость, тем больше Q0. Объемные резонаторы покрывают серебром (слой серебра
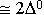, очень тонкий слой). 
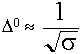. - Величина Q0 зависит от структуры поля в резонаторе, т.е. от типа колебаний в резонаторе. Для разных типов колебаний Q0 различна. Предположим, что магнитные поля в резонаторе всюду одинаковы
.
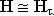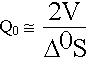
С объемом (V) связано накопление энергии, с поверхностью (S) связано рассеивание энергии. Глубина проникновения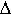 
0 связана с материалом. Q0 зависит от геометрических размеров (V и S). Увеличение V приводит к возникновению других типов. Q0 очень зависит от качества обработки внутренней поверхности резонатора (внутреннюю поверхность полируют)
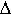0 в СВЧ: 10-5 
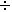10-6 М (очень мала)
размеры резонаторов пропорциональны длине волны:
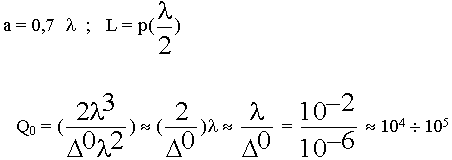
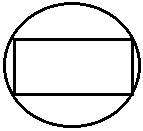
Сравнение Q0 от формы резонатора:
1) Прямоугольный резонатор в = 
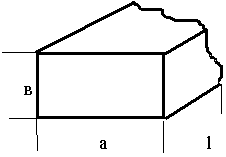
2) Квадратный резонатор
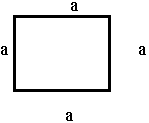
3) Круглый резонатор r = 
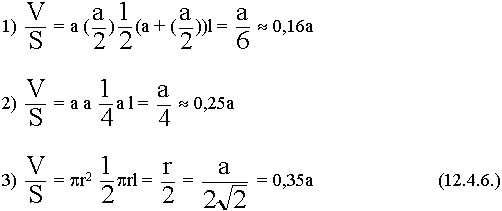
12.4.1. Нагруженная и внешняя добротности
На практике имеем:
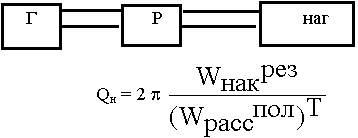
Нагруженная добротность - это отношение накопленной в резонаторе энергии к энергии рассеянной в резонаторе и в нагрузке за 1 период.
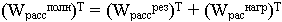
Рассмотрим величину 
с целью выяснения связи между Q0 и Qн, Qвн:
= 
= 
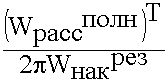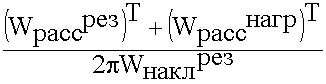
Qвн = 2p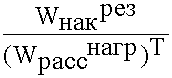 
- характеризует связь резонатора с нагрузкой
= 
+ 
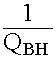(12.4.7.)
12.5. Режим связи резонатора с нагрузкой
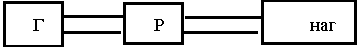
По степени связи резонатора с нагрузкой различают 3 режима работы:
1) Режим критической связи (критический режим).
Q0 = Qвн это означает, что энергия рассеяния в нагрузке равна энергии, потерянной в резонаторе.
(Wрассрез)Т = (Wрасснагр)Т
2) Режим пересвязи (сильная связь)
Q0 > Qвн (Wрассрез)Т < (Wрасснагр)Т
Вся энергия теряется на нагрузке.
3) Режим недосвязи (слабая связь)
Q0 < Qвн Большая часть энергии теряется в резонаторе. (Wрасрез)Т > (Wраснаг)Т
12.6. Измерение добротности
Qн = fрез / 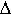f / на уровне 3 дБ
, дБ = 20 lg (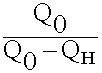
) (12.6.1.)
12.7. КПД объемного резонатора
= 
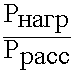
Отношение мощности, поступающей в нагрузку к мощности, рассеиваемой в резонаторе и нагрузке.
Рнагр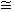 
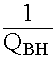Ррасс =
= 
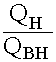= Qн (() - (
))
= 1 - (
) (12.7.1.)
Пример:
Q0 = 2000
= 1 - (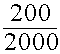
) = 0,9
Qн = 200
Список литературы
Основная
1. Вольман В.И., Пименов Ю.В. Техническая электродинамика. – М.: Связь, 1971.
2. Семенов Н.А. Техническая электродинамика. – М.: Связь, 1973.
3. Фальковский О.И. Техническая электродинамика. – М.: Связь, 1978.
4. Андрусевич Л.К., Беленький В.Г. Основы электродинамики. Новосибирск, СибГУТИ, 2000.
Дополнительная
Красюк Н.П., Дымович Н.Д. Электродинамика и распространение радиоволн. – М.: Высшая школа, 1974.
Федоров Н.Н. основы электродинамики. – М.: Высшая школа, 1980.
Никольский В.В., Никольская Т.Н. Электродинамика и РРВ. – М.: Высшая школа, 1973.
Вайнштейн Л.А. Электромагнитные волны, М.: Советское радио, 1957.
Гольдштейн А.Д., Зернов Н.В. Электромагнитные поля и волны. – М.: Советское радио, 1971.
Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся вузов, - М.: Наука, 1976.
Брунов В.Н., Гольдберг Л.Н., Кляцкин Н.Г., Цейтлин Л.А. Теория электромагнитного поля. – М.: Госэнергоиздат, 1962.
Методические указания к лабораторным работам. Новосибирск, СибГУТИ, 1999.