3.1. Радиотехнические цепи с обратной связью
3.2. Общая характеристика автоколебательной системы. Баланс амплитуд и баланс фаз
3.3. Автогенератор с трансформаторной обратной связью
3.1. Радиотехнические цепи с обратной связью
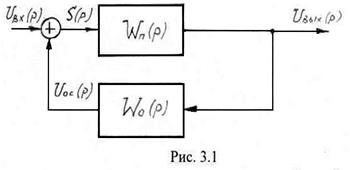 Радиотехнической цепью с обратной связью называется цепь у которой выходной сигнал вновь подается на вход цепи. На Рис. 3.1 представлена обобщенная структурная схема цепи с обратной связью (ЦОС). Из этого рисунка следует, что цепь с обратной связью является сложной, состоящей из цепи прямой связи и цепи обратной связи, через которую выходной сигнал возвращается на вход.
Радиотехнической цепью с обратной связью называется цепь у которой выходной сигнал вновь подается на вход цепи. На Рис. 3.1 представлена обобщенная структурная схема цепи с обратной связью (ЦОС). Из этого рисунка следует, что цепь с обратной связью является сложной, состоящей из цепи прямой связи и цепи обратной связи, через которую выходной сигнал возвращается на вход.
В практической радиотехнике обычно цепь прямой связи является активной (резонансный усилитель), а цепь обратной связи – пассивной цепью.
Для определения характеристик цепи с обратной связью воспользуемся операторным методом. Как известно, передаточная функция цепи:
![]() . (3.1)
. (3.1)
Но, как следует из Рис. 3.1:
![]() , (3.2)
, (3.2)
где ![]() – передаточная функция цепи прямой связи,
– передаточная функция цепи прямой связи,
![]() – сигнал рассогласования.
– сигнал рассогласования.
В свою очередь
![]() , (3.3)
, (3.3)
![]() , (3.4)
, (3.4)
где ![]() – сигнал обратной связи;
– сигнал обратной связи;
![]() – передаточная функция цепи обратной связи.
– передаточная функция цепи обратной связи.
Подстановка (3.4) в (3.3) и результата этой подстановки в (3.2) дает
![]() .
.
Откуда в соответствии с (3.1) следует, что передаточная функция цепи с обратной связью
![]() . (3.5)
. (3.5)
Комплексный коэффициент передачи ![]() определяется из (3.5) заменой
определяется из (3.5) заменой ![]()
![]() . (3.6)
. (3.6)
Так как
![]() , (3.7)
, (3.7)
![]() , (3.8)
, (3.8)
где ![]() ,
, ![]() – амплитудно-частотные характеристики (АЧХ),
– амплитудно-частотные характеристики (АЧХ), ![]() ,
, ![]() – фазо-частотные характеристики (ФЧХ), соответственно цепей прямой и обратной связи,
– фазо-частотные характеристики (ФЧХ), соответственно цепей прямой и обратной связи,
то подстановка (3.7) и (3.8) в (3.6) дает
![]() . (3.9)
. (3.9)
При ![]() ,
, ![]() , входной сигнал и сигнал обратной связи складываются синфазно и модуль комплексного коэффициента передача ЦОС
, входной сигнал и сигнал обратной связи складываются синфазно и модуль комплексного коэффициента передача ЦОС
![]() , (3.10)
, (3.10)
больше модуля комплексного коэффициента передачи цепи прямой связи. В этом случае обратная связь называется положительной.
Если же ![]() ,
, ![]() , то входной сигнал обратной связи складываются в противофазе и обратная связь называется отрицательной. При этом
, то входной сигнал обратной связи складываются в противофазе и обратная связь называется отрицательной. При этом
![]() . (3.11)
. (3.11)
Для оценки устойчивости цепей с обратной связью предложены различные критерии-правила, в соответствии с которыми можно судить устойчива цепь или нет.
Основной критерий устойчивости основан на решении характеристического уравнения
![]() , (3.12)
, (3.12)
где ![]() – коэффициенты линейного дифференциального уравнения, описывающего цепь
– коэффициенты линейного дифференциального уравнения, описывающего цепь
![]() .
.
Согласно основному критерию устойчивости цепь является устойчивой, если действительные части всех корней характеристического уравнения (3.12) отрицательны.
Помимо основного критерия используются алгебраический критерий Гурвица и частные критерии Михайлова и Найквиста, подробно изложенные в рекомендованной литературе.
В заключение отметим, что при ![]() , цепь с положительной обратной связью становится неустойчивой, т.е. в ней возникают незатухающие колебания. Это явление лежит в основе построения автогенераторов колебаний различной формы.
, цепь с положительной обратной связью становится неустойчивой, т.е. в ней возникают незатухающие колебания. Это явление лежит в основе построения автогенераторов колебаний различной формы.
3.2. Общая характеристика автоколебательной системы. Баланс амплитуд и баланс фаз
Обширный класс радиотехнических устройств составляют генераторы электромагнитных и электрических колебаний, которые используются для построения радиопередатчиков (задающие генераторы), радиоприемников (гетеродины), устройств радиоавтоматики и др. Все многообразие генераторов можно разделить на два класса: автогенераторы (генераторы с самовозбуждением) и генераторы с внешним возбуждением (по существу усилители). В зависимости от формы вырабатываемых колебаний различают генераторы гармонических колебаний и релаксационные генераторы. Последние вырабатывают колебания в виде, например, последовательности импульсов различной формы, колебания пилообразной формы и др. В дальнейшем основное внимание будет уделено автогенераторам гармонических колебаний.
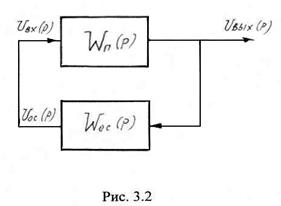 Автогенератор, в общем случае, представляет собой цепь с положительной обратной связью. При этом, на вход цепи прямой связи поступает не сигнал рассогласования
Автогенератор, в общем случае, представляет собой цепь с положительной обратной связью. При этом, на вход цепи прямой связи поступает не сигнал рассогласования ![]() , а непосредственно выходной сигнал
, а непосредственно выходной сигнал ![]() . Цепь прямой связи представляет собой активную цепь (резонансный усилитель с нагрузкой в виде колебательного контура), работающую в нелинейном режиме. Нелинейный режим работы активной цепи прямой связи является необходимым условием стационарности работы генератора в целом. В противном случае возникающие в цепи с обратной связью колебания должны были бы иметь бесконечно возрастающую амплитуду.
. Цепь прямой связи представляет собой активную цепь (резонансный усилитель с нагрузкой в виде колебательного контура), работающую в нелинейном режиме. Нелинейный режим работы активной цепи прямой связи является необходимым условием стационарности работы генератора в целом. В противном случае возникающие в цепи с обратной связью колебания должны были бы иметь бесконечно возрастающую амплитуду.
В соответствии с вышеизложенным обобщенная схема цепи с положительной обратной связью (автоколебательная система) имеет вид, изображение на рис. 3.2.
Анализ автоколебательной системы начнем в предположении, что система находится в стационарном режиме работы, т.е. все переходные процессы завершены и автогенератор генерирует колебания с частотой ![]() , которая определяется резонансной частотой нагрузки (контура) резонансного усилителя.
, которая определяется резонансной частотой нагрузки (контура) резонансного усилителя.
Так как в этом случае
![]() , (3.13)
, (3.13)
а ![]() определяется выражением (3.4), то подставляя (3.13) и (3.4) в (3.2) после преобразований получим
определяется выражением (3.4), то подставляя (3.13) и (3.4) в (3.2) после преобразований получим
![]() ,
,
или, сокращая обе части этого равенства на ![]()
![]() . (3.14)
. (3.14)
Производя замену ![]() найдем
найдем
![]() ,
,
или:
![]() . (3.15)
. (3.15)
Здесь ![]() и
и ![]() – коэффициенты усиления (передачи) цепей прямой и обратной связи на частоте
– коэффициенты усиления (передачи) цепей прямой и обратной связи на частоте ![]() , а
, а ![]() и
и ![]() – соответствующие фазовые сдвиги.
– соответствующие фазовые сдвиги.
Условие (3.15) выполняется при
![]() , (3.16)
, (3.16)
![]() , (3.17)
, (3.17)
где ![]() .
.
Соотношения (3.16) и (3.17) определяют соответственно баланс амплитуд и баланс фаз.
Условие баланса амплитуд означает, что в стационарном режиме работы автогенератора на генерируемой частоте ![]() полное усиление при обходе кольца обратной связи должно составлять единицу, а условие баланса фаз – полный фазовый сдвиг при обходе кольца обратной связи должен быть равен
полное усиление при обходе кольца обратной связи должно составлять единицу, а условие баланса фаз – полный фазовый сдвиг при обходе кольца обратной связи должен быть равен ![]() или кратен
или кратен ![]() .
.
Строго говоря, коэффициент усиления цепи прямой связи (резонансного усилителя) зависит не только от частоты ![]() , но и от амплитуды
, но и от амплитуды ![]() (из-за нелинейности ВАХ транзистора усилителя). В связи с этим, соотношение (3.16) принимает вид:
(из-за нелинейности ВАХ транзистора усилителя). В связи с этим, соотношение (3.16) принимает вид:
![]() ,
,
![]()
![]() . (3.18)
. (3.18)
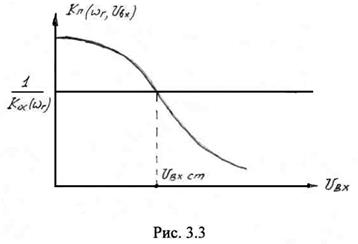 На рис. 3.3 построены зависимости
На рис. 3.3 построены зависимости ![]() и
и ![]() от величины
от величины ![]() . Так как
. Так как ![]() не зависит от
не зависит от ![]() , на графике
, на графике ![]() изображается прямой линией, параллельной оси
изображается прямой линией, параллельной оси ![]() . Эта линия называется прямой обратной связи. Что касается
. Эта линия называется прямой обратной связи. Что касается ![]() , то с ростом
, то с ростом ![]()
![]() уменьшается за счет нелинейности ВАХ транзистора. Когда усиление
уменьшается за счет нелинейности ВАХ транзистора. Когда усиление ![]() достигает величины
достигает величины ![]() , т.е. выполняется условие (3.18), дальнейший рост
, т.е. выполняется условие (3.18), дальнейший рост ![]() прекращается и генератор переходит в стационарный режим. Проекция точки пересечения прямой обратной связи и кривой
прекращается и генератор переходит в стационарный режим. Проекция точки пересечения прямой обратной связи и кривой ![]() на ось
на ось ![]() даст значение
даст значение ![]() в стационарном режиме.
в стационарном режиме.
3.3. Автогенератор с трансформаторной обратной связью
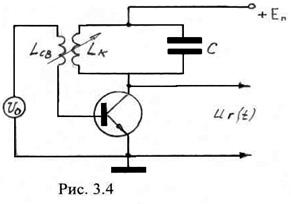
Принципиальная схема автогенератора с трансформаторной обратной связью представлена на рис. 3.4. Автогенератор представляет собой резонансный усилитель, нагрузкой которого служит высокодобротный колебательный контур ![]() ,
, ![]() , а обратная связь осуществляется при помощи индуктивности
, а обратная связь осуществляется при помощи индуктивности ![]() . Коэффициент взаимной индукции
. Коэффициент взаимной индукции
![]() ,
,
откуда следует, что коэффициент обратной связи
![]() . (3.19)
. (3.19)
Качественно механизм самовозбуждения может быть описан следующим образом. При включении источника питания за счет, например, тепловых шумов возникают колебания, в спектре которых содержится составляющая с частотой, равной резонансной частоте контура. Эта составляющая выделяется на контуре и через цепь обратной связи (трансформатор) подается на базу транзистора. Происходит усиление этой составляющей и цикл повторяется. Имеет место лавинно-образный процесс нарастания амплитуды колебаний. На этом этапе усилитель работает в линейном режиме, т.е. ведет себя как активная линейная цепь (рис. 3.5). Однако по мере нарастания амплитуды колебаний усилитель переходит в нелинейный режим, характерный для усилителя, работающего с отсечкой тока. При этом рост амплитуды замедляется, и генератор приходит к стационарному режиму генерирования колебаний.
Определим условия самовозбуждения генератора. Так как в качестве цепи прямой связи используется резонансный усилитель, то в линейном режиме его АЧХ описывается выражением
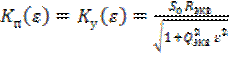 ,
,
где ![]() – удвоенная относительная расстройка,
– удвоенная относительная расстройка,
![]() – крутизна ВАХ транзистора,
– крутизна ВАХ транзистора,
![]() и
и ![]() – соответственно эквивалентное сопротивление и эквивалентная добротность нагрузки.
– соответственно эквивалентное сопротивление и эквивалентная добротность нагрузки.
В момент запуска автогенератора относительная расстройка ![]() и коэффициент усиления цепи прямой связи на частоте
и коэффициент усиления цепи прямой связи на частоте ![]()
![]() .
.
Колебание возникает, если будет выполнено условие:
![]() ,
,
где ![]() определяется выражением (3.19).
определяется выражением (3.19).
Отсюда следует условие самовозбуждения автогенератора с трансформаторной обратной связью
![]() . (3.20)
. (3.20)
Критическое значение коэффициента обратной связи вытекает из условия баланса амплитуд (3.16)
![]() . (3.21)
. (3.21)
Очевидно, при этом значении ![]() имеет место стационарный режим работы автогенератора.
имеет место стационарный режим работы автогенератора.
Для анализа и расчета характеристик автогенератора в стационарном режиме необходимо задать аппроксимацию ВАХ транзистора. Рассмотрим степенную аппроксимацию
![]() (3.22)
(3.22)
Очевидно, производная
![]() , (3.23)
, (3.23)
определяет дифференциальную крутизну ВАХ транзистора. В автогенераторе на базу транзистора через цепь обратной связи поступает напряжение
![]() . (3.24)
. (3.24)
Коллекторный ток в соответствии с (1.10) будет определяться выражением:
![]()
Амплитуды гармонических составляющих тока зависят от амплитуды входного напряжения ![]() на базе транзистора. Так как нагрузкой усилителя является высокодобротный контур, настроенный на частоту
на базе транзистора. Так как нагрузкой усилителя является высокодобротный контур, настроенный на частоту ![]() , то пренебрегая высшими гармоническими составляющими, получим приближенное значение коллекторного тока
, то пренебрегая высшими гармоническими составляющими, получим приближенное значение коллекторного тока
![]() . (3.25)
. (3.25)
Так как в стационарном режиме ![]() , соотношение (3.25) принимает вид
, соотношение (3.25) принимает вид
![]() . (3.26)
. (3.26)
Дифференциальную крутизну (3.23) представим в виде
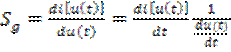 . (3.27)
. (3.27)
Проведя операцию дифференцирования с учетом (3.24) и (3.27), получим
![]() . (3.28)
. (3.28)
Величина ![]() называется средней крутизной или крутизной по первой гармонике ВАХ транзистора. С учетом средней крутизны условие (3.20) самовозбуждения автогенератора принимает вид
называется средней крутизной или крутизной по первой гармонике ВАХ транзистора. С учетом средней крутизны условие (3.20) самовозбуждения автогенератора принимает вид
![]() ,
,
или
![]() . (3.29)
. (3.29)
Найдем амплитуду напряжения колебаний автогенератора в стационарном режиме при степенной аппроксимации ВАХ полиномом третьей степени
![]() .
.
Для определения средней крутизны следует положить
![]() .
.
Тогда
![]() .
.
Воспользовавшись тригонометрическим соотношением
![]() ,
,
получим
![]() .
.
Амплитуда первой гармоники тока
![]() ,
,
и средняя крутизна в соответствии с (3.28)
![]() (3.30)
(3.30)
Условие баланса амплитуд (стационарный режим) определяется выражением
![]() .
.
Подстановка в это выражение выражения (3.30) при ![]() и решение полученного уравнения относительно
и решение полученного уравнения относительно ![]() дает
дает
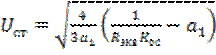 . (3.31)
. (3.31)
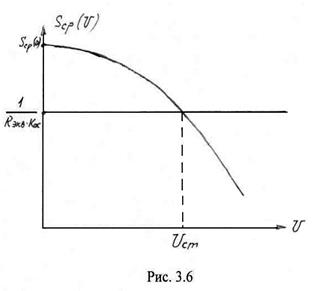 На рис. 3.6 приведена графическая интерпретация определения амплитуды колебаний автогенератора в стационарном режиме. При приведенной аппроксимации ВАХ полиномом третьей степени коэффициент
На рис. 3.6 приведена графическая интерпретация определения амплитуды колебаний автогенератора в стационарном режиме. При приведенной аппроксимации ВАХ полиномом третьей степени коэффициент ![]() . Тогда график
. Тогда график ![]() , определяемый (3.30), представляет собой монотонно убывающую кривую, начиная с
, определяемый (3.30), представляет собой монотонно убывающую кривую, начиная с ![]() . Прямая обратной связи в этом случае имеет значение
. Прямая обратной связи в этом случае имеет значение ![]() . Пересечение кривой
. Пересечение кривой ![]() с прямой обратной связи дает значение
с прямой обратной связи дает значение ![]() .
.
3.4. Мягкий и жесткий режимы самовозбуждения автогенератора
От выбора рабочей точки (напряжения смещения ![]() ) ВАХ транзистора зависит точность аппроксимации, что в свою очередь, в значительной степени определяет характер самовозбуждения автогенератора. Рассмотрим степенную аппроксимацию ВАХ полиномом пятой степени
) ВАХ транзистора зависит точность аппроксимации, что в свою очередь, в значительной степени определяет характер самовозбуждения автогенератора. Рассмотрим степенную аппроксимацию ВАХ полиномом пятой степени
![]() . (3.32)
. (3.32)
Проводя преобразования аналогичные преобразованиям для определения ![]() (выражение (3.30)) с использованием тригонометрического соотношения
(выражение (3.30)) с использованием тригонометрического соотношения
![]() ,
,
найдем амплитуду первой гармоники коллекторного тока:
![]() ,
,
откуда следует:
![]() . (3.33)
. (3.33)
На рис. 3.7 приведены графики ![]() при различных значениях коэффициентов
при различных значениях коэффициентов ![]() и
и ![]() .
.
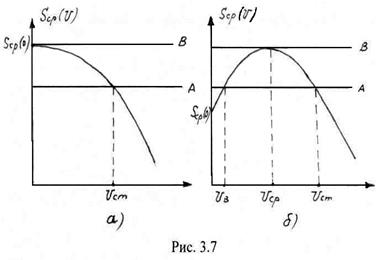 При
При ![]() и
и ![]() , зависимость
, зависимость ![]() представляет собой монотонно убывающую кривую (рис. 3.7а), которая при
представляет собой монотонно убывающую кривую (рис. 3.7а), которая при ![]() имеет значение
имеет значение ![]() .
.
Пусть ![]() и
и ![]() . При малых амплитудах квадратичное слагаемое в (3.33) преобладает над слагаемым четвертой степени и вначале
. При малых амплитудах квадратичное слагаемое в (3.33) преобладает над слагаемым четвертой степени и вначале ![]() возрастает с увеличением
возрастает с увеличением ![]() . При дальнейшем амплитуды отрицательное слагаемое четвертой степени оказывает решающее влияние и кривая
. При дальнейшем амплитуды отрицательное слагаемое четвертой степени оказывает решающее влияние и кривая ![]() , достигнув максимума, начинает убывать (рис.3.7б).
, достигнув максимума, начинает убывать (рис.3.7б).
Возвратимся к выражению (3.29). Правая часть неравенства представляет собой прямую обратной связи. Прямая обратной связи на графиках рис. 3.7 изображается в виде прямой, параллельной оси абсцисс ![]() , а ее положение на графике определяется значением
, а ее положение на графике определяется значением ![]() .
.
Рассмотрим режимы самовозбуждения при различных значениях коэффициентов ![]() и
и ![]() . В случае
. В случае ![]() и
и ![]() , при включении автогенератора, условие (3.29) выполняется (положение А прямой обратной связи), колебания возникают и их амплитуда плавно нарастает до значения
, при включении автогенератора, условие (3.29) выполняется (положение А прямой обратной связи), колебания возникают и их амплитуда плавно нарастает до значения ![]() , определяемого точкой пересечения кривой
, определяемого точкой пересечения кривой ![]() и прямой обратной связи. Очевидно, при уменьшении
и прямой обратной связи. Очевидно, при уменьшении ![]() амплитуда колебаний плавно уменьшается и при
амплитуда колебаний плавно уменьшается и при ![]() , происходит срыв колебаний (положение В прямой обратной связи). Такой режим самовозбуждения получил название мягкого режима. Он характеризуется тем, что возникновение и срыв колебаний происходит при одном и том же значение
, происходит срыв колебаний (положение В прямой обратной связи). Такой режим самовозбуждения получил название мягкого режима. Он характеризуется тем, что возникновение и срыв колебаний происходит при одном и том же значение ![]() .
.
В случае ![]() и
и ![]() (рис. 3.7б) имеют место две точки пересечения кривой
(рис. 3.7б) имеют место две точки пересечения кривой ![]() и прямой обратной связи. При включении автогенератора значение
и прямой обратной связи. При включении автогенератора значение ![]() лежит ниже прямой обратной связи, условие (2.39) не выполняется и колебания не возникают. Для возникновения колебаний необходимо внешнее воздействие от вспомогательного генератора с амплитудой
лежит ниже прямой обратной связи, условие (2.39) не выполняется и колебания не возникают. Для возникновения колебаний необходимо внешнее воздействие от вспомогательного генератора с амплитудой ![]() . При этом генератор скачкообразно (жестко) переходит в режим генерирования колебаний. Однако так как часть кривой
. При этом генератор скачкообразно (жестко) переходит в режим генерирования колебаний. Однако так как часть кривой ![]() располагается выше прямой обратной связи, амплитуда колебаний будет нарастать до тех пор, пока не достигнет величины
располагается выше прямой обратной связи, амплитуда колебаний будет нарастать до тех пор, пока не достигнет величины ![]() , определяемого точкой пересечения кривой
, определяемого точкой пересечения кривой ![]() и прямой обратной связи. При уменьшении значения
и прямой обратной связи. При уменьшении значения ![]() прямая обратной связи поднимается вверх и при достижении положения В происходит срыв колебаний. Амплитуда колебаний при срыве, как следует из рисунка, составляет
прямая обратной связи поднимается вверх и при достижении положения В происходит срыв колебаний. Амплитуда колебаний при срыве, как следует из рисунка, составляет ![]() . Такой режим самовозбуждения называется жестким режимом. Он отличается тем, что возникновение колебаний и срыв происходят скачкообразно при различных значениях
. Такой режим самовозбуждения называется жестким режимом. Он отличается тем, что возникновение колебаний и срыв происходят скачкообразно при различных значениях ![]() .
.
Для реализации мягкого режима самовозбуждения рабочую точку выбирают на участке ВАХ с наибольшей крутизной (точка А на рис. 3.8). Что касается жесткого режима, то рабочая точка находится в нижней части ВАХ нелинейного элемента (точка В на рис 3.8). Таким образом, в жестком режиме автогенератор работает с отсечкой тока, что энергетически более выгодно и является достоинством этого режима. Достоинством же мягкого режима являются благоприятные условия для запуска генератора.
3.5. Трехточечные автогенераторы гармонических колебаний
На практике более широкое распространение получили трехточечные автогенераторы. Основой таких автогенераторов является параллельный ![]() - контур, который подключается к нелинейному элементу (лампе или транзистору) тремя точками (отсюда и название автогенераторов). Напряжение обратной связи в таких генераторах снимается с части контура. В зависимости от того, какой элемент контура служит для образования обратной связи различают генераторы с емкостной обратной связью (емкостная трехточка) и генераторы с индуктивной обратной связью (индуктивная трехточка).
- контур, который подключается к нелинейному элементу (лампе или транзистору) тремя точками (отсюда и название автогенераторов). Напряжение обратной связи в таких генераторах снимается с части контура. В зависимости от того, какой элемент контура служит для образования обратной связи различают генераторы с емкостной обратной связью (емкостная трехточка) и генераторы с индуктивной обратной связью (индуктивная трехточка).
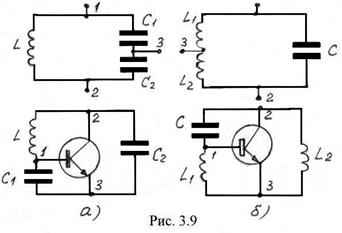 На рис. 3.9 изображены контура с точками подключения к активному элементу и соответствующие схемы автогенераторов без вспомогательных элементов.
На рис. 3.9 изображены контура с точками подключения к активному элементу и соответствующие схемы автогенераторов без вспомогательных элементов.
В генераторе с емкостной обратной связью (рис.3.9 а) напряжение обратной связи снимается с конденсатора ![]() .
.
Коэффициент обратной связи этого автогенератора составляет
![]() , (3.34)
, (3.34)
где ![]() и
и ![]() – соответственно комплексные амплитуды напряжений на емкости
– соответственно комплексные амплитуды напряжений на емкости ![]() и на контуре. С другой стороны
и на контуре. С другой стороны
![]() , (3.35)
, (3.35)
![]() , (3.36)
, (3.36)
где ![]() – комплексная амплитуда тока, протекающего через контур.
– комплексная амплитуда тока, протекающего через контур.
Подстановка (3.35) и (3.36) в (3.34) дает
![]() . (3.37)
. (3.37)
Так как коэффициент усиления усилителя по первой гармонике
![]() ,
,
то, исходя из баланса амплитуд, с учетом (3.37), можно записать
![]() . (3.38)
. (3.38)
При соблюдении баланса фаз, уравнение (3.37) определяет условие самовозбуждение емкостной трехточки.
Частота колебаний такого генератора
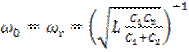 . (3.39)
. (3.39)
Аналогичные рассуждения для индуктивной трехточки приводят к уравнению баланса амплитуд
![]() , (3.40)
, (3.40)
где коэффициент обратной связи
![]() . (3.41)
. (3.41)
Частота колебаний индуктивной трехточки
![]() . (3.42)
. (3.42)

