Мы уже отмечали, что развитие вычислительной техники привело к появлению цифровых систем обработки сигналов. При этом как сигнал, так и его спектр необходимо перед вводом в вычислительное устройство представлять в виде отсчетов, т.е. в виде чисел.
В формулах (5) и (6), или (7) и (8), один из компонентов уже является дискретным. Остается только заменить в этих формулах оставшуюся непрерывную переменную (t или f) дискретными значениями.
Так, например, если в формулах (5) и (6) время t заменим на nT, то получим формулы (9) и (10)
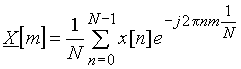 , (9)
, (9)
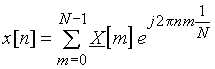 . (10)
. (10)
Следует заметить, что при этом периодический сигнал ![]() стал дискретным сигналом
стал дискретным сигналом ![]() , или
, или ![]() , а значит дискретный спектр
, а значит дискретный спектр ![]() начал периодически повторяться (рис. 17). Суммирование дискретных составляющих спектра
начал периодически повторяться (рис. 17). Суммирование дискретных составляющих спектра ![]() в формуле (6) следует теперь вести не в бесконечных пределах, а на периоде, где укладывается N отсчетов. Значит индекс суммирования m в формуле (10) будет изменяться от m = 0 до m = N – 1.
в формуле (6) следует теперь вести не в бесконечных пределах, а на периоде, где укладывается N отсчетов. Значит индекс суммирования m в формуле (10) будет изменяться от m = 0 до m = N – 1.
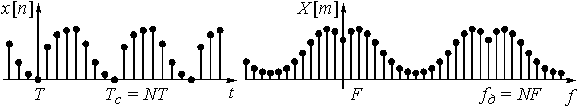
Рис.17
На периоде повторения ![]() дискретного сигнала
дискретного сигнала ![]() также укладывается N отсчетов, включая нулевой отсчет. Интеграл в (5) заменяется суммой с индексом суммирования n, изменяющимся от n = 0 до n = N – 1. Переменная dt в этой формуле при переходе от интеграла к сумме заменяется на T, так что отношение
также укладывается N отсчетов, включая нулевой отсчет. Интеграл в (5) заменяется суммой с индексом суммирования n, изменяющимся от n = 0 до n = N – 1. Переменная dt в этой формуле при переходе от интеграла к сумме заменяется на T, так что отношение ![]() , т.к.
, т.к. ![]() . Частота дискретизации равна
. Частота дискретизации равна ![]() . Отсюда вытекают соотношения:
. Отсюда вытекают соотношения:
![]() и
и ![]() . (11)
. (11)
Произведение FT можно заменить величиной 1/N.
Выражения (9) и (10) называются прямым и обратным дискретным преобразованием Фурье.
Вывод: Формулы дискретного преобразования Фурье (ДПФ) удобны для расчетов на ЭВМ.
Пример 8.1. Рассчитаем ДПФ дискретного периодического сигнала, заданного тремя отсчетами ![]() = {0; 1; 2}.
= {0; 1; 2}.
Для расчета воспользуемся формулой ДПФ (9).
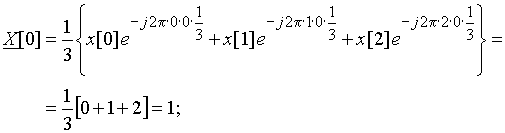
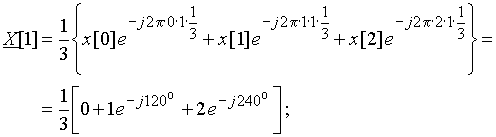
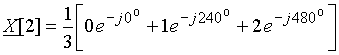 .
.
Поскольку
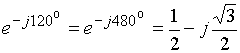 ,
, 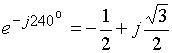 ,
,
то ![]() ,
,
![]() .
.
Графики заданного дискретного периодического сигнала ![]() и рассчитанного дискретного периодического спектра амплитуд
и рассчитанного дискретного периодического спектра амплитуд ![]() приведены на рис. 18.
приведены на рис. 18.
Пример 8.2. Рассчитаем значения дискретного сигнала ![]() , ДПФ которого имеет вид
, ДПФ которого имеет вид ![]() = {0; 1; 0; 1}.
= {0; 1; 0; 1}.
Значения дискретного сигнала ![]() будем рассчитывать по формуле (10)
будем рассчитывать по формуле (10)
![]() ;
;
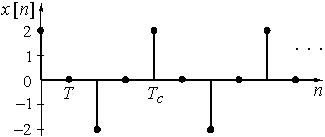
Рис. 19
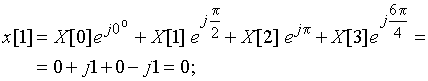
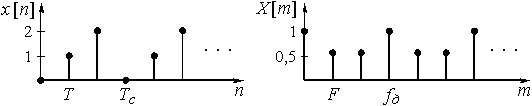
Рис. 18
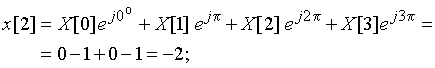
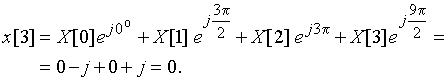
График последовательности ![]() = {2; 0; –2; 0} приведен на рис. 19. Сигнал
= {2; 0; –2; 0} приведен на рис. 19. Сигнал ![]() дискретный и периодический.
дискретный и периодический.
Самоконтроль
1. Как рассчитать спектр дискретного периодического сигнала?
2. Как рассчитать дискретный периодический сигнал по его спектру?
3. Найдите ДПФ сигнала, заданного двумя отсчетами ![]() = {1; –1}.
= {1; –1}.
4. Рассчитайте значения ![]() и
и ![]() дискретного сигнала, ДПФ которого имеет вид
дискретного сигнала, ДПФ которого имеет вид ![]() = {1; –1}.
= {1; –1}.

