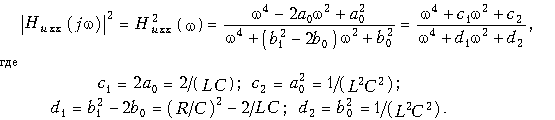Рабочее ослабление четырехполюсника. Режим согласованного включения четырехполюсника является наиболее благоприятным для передачи энергии. Однако обеспечить идеальное согласование четырехполюсника с генератором и нагрузкой в широкой полосе частот возможно только в том случае, когда внутреннее сопротивление генератора, сопротивление нагрузки и характеристические сопротивления четырехполюсника являются резистивными. Добиться же равенства комплексных сопротивлений на всех частотах рабочего диапазона, как правило, не удается. Возникающая вследствие этого несогласованность приводит к дополнительным потерям энергии.

Рассмотрим работу четырехполюсника в реальных условиях (см. рис. 12.1), когда Zг № Zс1 и Zн № Zс2. В этом случае Zвх1 № Zг и Zвх2 № Zн. Несогласованность на входе приводит к тому, что часть энергии отражается от входных зажимов четырехполюсника и возвращается к генератору. Изза несогласованности на выходе не вся энергия из четырехполюсника передается нагрузке: часть ее отражается от нагрузки и возвращается обратно в четырехполюсник. Очевидно, какаято часть энергии будет теряться за счет многократного ее отражения на входных и выходных зажимах четырехполюсника.

Чтобы учесть дополнительно возникающие в рабочих условиях потери энергии, пользуются рабочими мерами передачи, которые являются внешними характеристиками четырехполюсника.

К внешним характеристикам относится рабочее ослабление четырехполюсника, которое позволяет сравнить в логарифмических единицах полную мощность S2, выделяемую в нагрузке Zн на выходе четырехполюсника, с полной мощностью S0, которую генератор отдает в нагрузку, согласованную с его внутренним сопротивлением.

Мощность, выделяемая в нагрузке Zн (см. рис. 12.1)

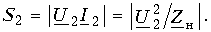
Полная мощность S0 выделяется на сопротивлении, равном внутреннему сопротивлению генератора, т. е. на Zг, и подключенном непосредственно к его зажимам:

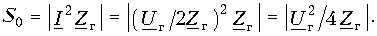
Рабочее ослабление четырехполюсника, выраженное в неперах (Нп), подсчитывается по формуле

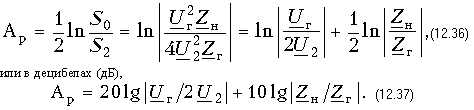
В (12.36) и (12.37) входят действующие значения Uг и U2, которые могут быть измерены экспериментально, поэтому эти формулы лежат в основе большинства методов измерения рабочего ослабления четырехполюсника.

При теоретических расчетах пользуются другой формулой

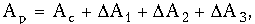
где Ac - характеристическое ослабление четырехполюсника; DA1, DA2 - дополнительные ослабления изза несогласованностей на входе и выходе четырехполюсника:

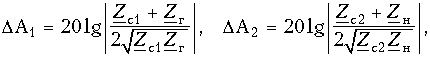
DA3 - дополнительное ослабление за счет многократного отражения энергии от входных и выходных зажимов четырехполюсника:

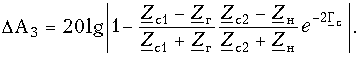
При согласовании четырехполюсника с генератором Zг = Zc1 и DA1 = DA3 = 0. При согласовании четырехполюсника с нагрузкой Zн = Zc2 и DA2 = DA3 = 0.

Если согласование полное, т. е. Zг = Zc1 и Zн = Zc2, то Ар = Ас, т. е. рабочее ослабление четырехполюсника равно его характеристическому (собственному) ослаблению. Для пассивного четырехполюсника рабочее ослабление больше собственного ослабления вследствие рассогласования на входе и выходе.

Рабочее ослабление является вещественной частью комплексной величины Гр - рабочей постоянной передачи четырехполюсника:

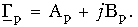
где Вр - рабочая фазовая постоянная.

Передаточные функции четырехполюсника. Передаточной функ-цией нагруженного четырехполюсника (см. рис. 12.1) называется отношение выходной электрической величины к входной электрической величине, т. е. отношение реакции к воздействию.

Если входным воздействием считать напряжение генератора с комплексным действующим значением Uг, а реакцией четырехполюсника на это воздействие - напряжение с комплексным действующим значением U2 или ток с комплексным действующим значением I2, то получаются комплексные передаточные функции общего вида:

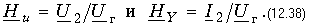
В частных случаях, когда заданными воздействиями являются напряжение на входных зажимах четырехполюсника или ток, протекающий через эти зажимы, получают следующие четыре разновидности передаточных функций:

Hu = U2/U1 - комплексный коэффициент передачи по напряжению (для активных четырехполюсников, например усилителей, он носит название коэффициента усиления по напряжению);

Hi = I2/I1 - комплексный коэффициент передачи по току (для активных цепей - коэффициент усиления по току);

HZ = U2/I1 - комплексное передаточное сопротивление;

HY = I2/U1 - комплексная передаточная проводимость.

Передаточные функции четырехполюсника выражаются через любую систему параметров и сопротивления нагрузки. Например,

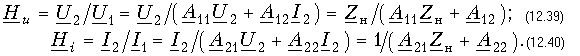
Можно вычислять передаточные функции в различных режимах работы четырехполюсника (холостой ход, короткое замыкание, согласованное включение). Например, при холостом ходе на выходе (разомкнутые зажимы 2-2') комплексный коэффициент передачи по напряжению находится из (12.39) при Zн = Ґ

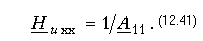
Коэффициент передачи по току в режиме короткого замыкания на выходе (замкнутые накоротко зажимы 2-2') получим из (12.40) при Zн = 0:

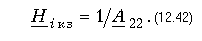
При согласованном включении симметричного четырехполюсника из (12.39) следует

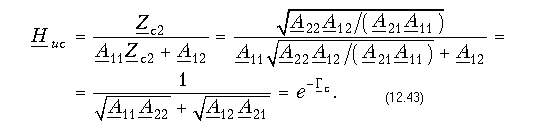
Формула (12.43) устанавливает связь между передаточной функцией по напряжению согласованно включенного симметричного четырехполюсника с его характеристической (собственной) постоянной передачи. Аналогичным образом можно получить остальные передаточные функции в различных режимах работы и выражения их через интересующие нас параметры.

Часто используют так называемую рабочую передаточную функцию четырехполюсника:

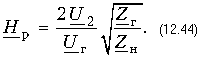
Рабочая передаточная функция непосредственно связана с рабочей постоянной передачи четырехполюсника. Действительно, из (12.44) и (12.36) вытекает, что

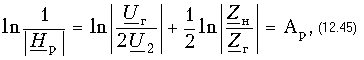
Справедливы также более общие соотношения: или .

Если на входе четырехполюсника действует негармоническое (периодическое или непериодическое) воздействие, то, переходя от мгновенных значений напряжений и токов к их изображениям по Лапласу Uг(p), U1(p), U2(p), I1(p) и I2(p), получают операторные передаточные функции Н(р), которые представляются в общем виде (7.41):

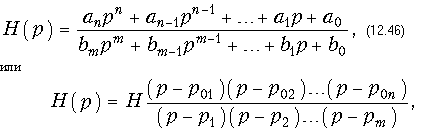
где р01, р02, ..., р0n - нули передаточной функции; р1, р2, ..., рm - полюса передаточной функции; Н = ап/bт.

Пример. Найдем коэффициент передачи по напряжению и квадрат АЧХ четырехполюсника, изображенного на рис. 12.18, a, в режиме XX на выходных зажимах.

Коэффициент передачи по напряжению нагруженного четырехполюсника согласно (12.39)

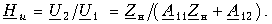
В режиме XX Zн = Ґ и согласно (12.41) и (12.8)

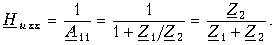
Используя операторную форму записи, имеем

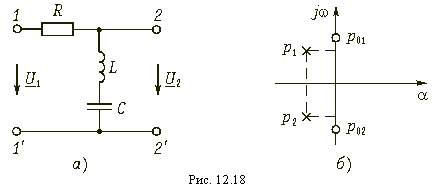
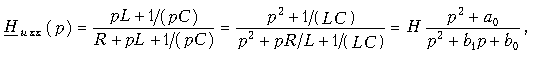
где H = 1; a0 = b0 = 1/LС; b1 = R/L.

Корни числителя этой рациональной дроби, т. е. нули передаточной функции,

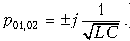
Корни знаменателя, или полюсы передаточной функции,

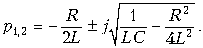
На рис. 12.18, б показано расположение нулей и полюсов функции при .

По теореме Виета

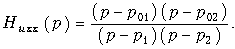
Амплитудночастотная характеристика в данном режиме работы определяется из Huхх(р) путем замены р на jw и вычисления модуля полученной функции

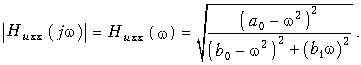
Квадрат АЧХ запишется в виде